考虑距离影响的公交网络敏感度

2021-02-01杜牧青虞春滨

西南交通大学学报 2021年1期

杜牧青，虞春滨

（河海大学土木与交通学院，江苏南京 210098）

敏感度分析是令模型的参数在某一特定范围内变动，以观察模型结果变化的一种定量化分析方法，它主要用于研究模型或系统由于输入的扰动而造成输出结果的不确定性. 敏感度分析的最简单方式是通过每次改变一个输入变量的值，观测模型输出结果的变化. 然而，面对如交通网络的大型系统时，想要观测每个网络要素属性变化对交通网络系统运行状态的影响，是无法采用观测试验来完成的. 为此，提出具有解析表达式的交通网络敏感度分析方法，具有重要的实际意义. 近年来，解析的敏感度分析在区域交通控制和道路网络运营方面，已经得到大量关注[1-4]. 该方法的主要目的是将路段流量和/或路径旅行费用作为成本和需求函数改变的函数，然后量化其变化率. 分析的结果可以用于优化目标，如控制减少交通流量或者减少拥挤路段上的旅行时间.

出行距离是影响出行者路径选择的一个不可或缺的因素[5]. 随着城市化进程不断推进，出行策略的选择变得多样. 显然，不同策略的出行距离是不同的. 随出行距离的增加，出行者所花费的出行成本也会上升. 特别是在拥挤的情况下，出行者会因为旅行距离的增加，感知到的阻抗会比一般情况下大. 所以，考虑距离因素对于流量分配有着现实作用，更加符合出行者路径选择的心理状态. 这种现象在拥挤的公交出行中表现更明显，但以往研究极少考虑出行距离对出行费用的影响.

对于公交网络敏感度分析的研究相对较少. 较早开展此类研究的Lee等[6]进行了一些基于敏感度的数值实验，考虑了需求变化、旅行时间和换乘惩罚，但没有得到敏感度的解析表达式. 之后Gao等[7]推导了基于路径表达的公交分配模型的敏感度，用于求解双层公交网络设计问题，这种方法基于路径表达的方式，可以近似地将公交网络分配转化为普通道路网络分配，不过该方法会产生不合理的公交换乘路径. 随后Jiang等[8]提出了修正的网络表达方式来处理这种情况，但是需要把原有网络扩展得很大，降低了问题的求解效率.

公交分配模型是进行敏感度分析的基础，在公交系统的运营和规划中起着重要作用. Cea等[9]较早提出了考虑拥挤情况下的公交分配问题的用户均衡分配模型，并且引入了换乘路径和有效频率的概念.随后，针对公交用户均衡分配问题，Wu等[10]拓展了文献[11]中基于发车频率的公交分配模型，进一步将费用函数扩展为非对称形式，把等待费用和车内旅行费用都表示为流量的函数；同时采用弧段-超路径形式的关联矩阵来表示弧段流量和超路径流量的关系. 以上研究都是从模型改进和优化策略的角度考虑的，没有考虑距离因素对于出行者感知费用的影响. 特别在公交分配中对于距离因素没有进行分析，这在一定程度会影响出行选择并对公交分配产生一定的影响，从而使得敏感度分析结果和实际有较大偏差.

基于存在的问题，本文采用经典的超路径理论来解释公交共线问题[12]. 在考虑距离因素的情况下，用解析的形式构建了公交网络均衡分配的敏感度分析方法. 最后，对比分析了考虑距离因素对于结果的影响，并对具体参数进行了分析，为更加合理的公交网络规划提供了理论依据.

1 公交网络均衡问题

1.1 距离影响作用

距离对于出行者的选择行为有着一定影响[5]，并且在公交出行中较为明显. 由于公交车的载客量没有统一的标准，所以在拥挤的时候个人空间很少，乘客表现出不舒适感[13]，并且这种不舒适感随着距离的增加呈现加重趋势，最终体现在感知费用中. 传统的模型中费用只与时间和流量有关，而距离只与行驶或者步行时间有关. 但是出行者实际感知的费用会因为距离的增加适度放大. 特别在拥挤的情况下，会大大增加费用，感知费用和时间的关系见图1.

图1 感知费用示意Fig. 1 Diagram of perceptual cost

图1 中，当旅行时间很短时，距离的影响作用很小；随着时间的增大，距离的影响作用就显现出来，导致感知费用增长加快，图中表现为斜率的变大，即不舒适感随着距离的增加不断加重. 这符合乘客实际出行的心理状况，在其他条件相同情况下，出行距离会影响其感知阻抗. 这里的感知阻抗特指在乘客在车内旅行时候感知到的阻抗.由此，需要考虑距离对于出行者的影响，并将其运用到流量分配中，使得结果更符合实际情况.

1.2 考虑距离影响的弧段费用

公交分配是基于公交分配模型的. 本文以文献[10]的模型为基础，该模型具有一定的代表性，并且能够较好地反映距离这一影响因素.

将公交网络定义为一个有向图G(N，A)，其中N为节点集合，包含站点集、线路连接点集和起讫点集，A为弧段集合，包含车内旅行弧段集A1、等车弧段集A2、步行弧段集A3和下车弧段集A4. 弧段具有三重属性，分别为零流时间ta、发车频率fa和距离La. 图2为4种弧段的公交网络节点扩展示意. 其中，车内旅行弧段为1条公交线路中连接连续2个线路连接点的弧段；等车弧段为乘客等待公交的弧段；下车弧段是由公交线路连接点到公交站点的弧段，表示乘客下车到公交站进行换乘或者准备到目的地；步行弧段表示起讫点与公交站点的弧段.

图2 公交网络节点扩展示意Fig. 2 Expansion diagram of transit network nodes

为考虑拥挤效应，假定公交网络弧段上的拥挤费用为相关弧段上流量的函数，为流量. 弧段上的拥挤费用不但与自身流量有关，而且与其他相关弧段上的流量有关[10]. 这里主要考虑等车弧段和车内旅行弧段上的拥挤费用，具体的流量流向关系见图3.图中，、、和分别为上车流量、下游流量、下车流量和上游流量，且为直接乘客流量.

图3 线路连接点流量流向关系Fig. 3 Flow relationship of line connection point

进一步，考虑距离影响的广义出行费用，做以下假定：1）步行弧段费用只与步行时间有关，当步行时间越长，感受到的费用越大； 2）不考虑下车弧段费用与距离的关系； 3）等车弧段的广义费用由等车时间和拥挤费用组成； 4）车内旅行弧段的广义费用由票价、适度放大的拥挤费用和车内旅行时间组成.

本文主要讨论图1中距离因素的影响，为此构建车内旅行弧段a的广义费用为

式中：m为待定参数；d为出行者对距离的敏感程度.

此外，结合已有经验公式[10]，得到等车弧段、步行弧段和下车弧段的广义费用分别为式（3）～（5）.

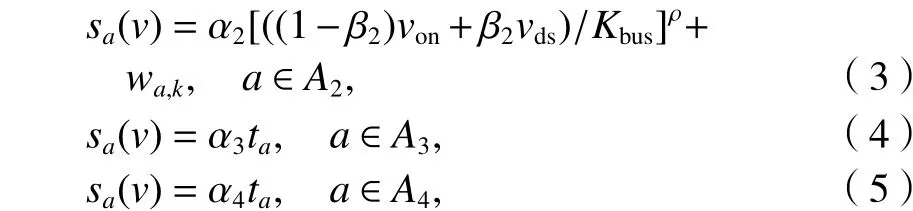
1.3 超路径均衡分配理论

公交网络的复杂之处在于共线问题. 出行者在某一个站点存在多种策略去往终点，为了解决此类问题，超路径理论被广泛采用. 超路径图是一个有向图，遵循流量分配规则[14]. 乘客的行为遵行公交先来先上车的原则，而对于那些超出自己的期望花费的策略则不予考虑[12]. 由此，乘客可根据实际情况做出相应决策.

首先定义部分符号和变量：

ptail(a)为乘车∑在超路径k上选择弧段a节点的概率，且有

由此，可以得到在超路径k上的旅行费用为[10]

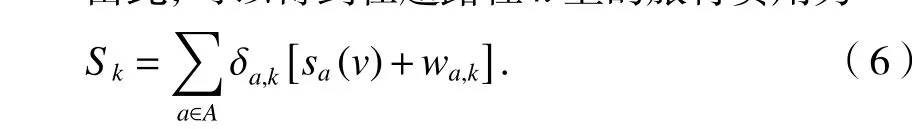
采用向量的形式表示为

令

根据式（1），广义的旅行费用是流量的函数，并且考虑了距离的影响. 当公交网络中产生新的需求后，原来的最优解可能不再最优. 这里假定公交网络满足Wardrop的用户均衡条件，乘客将会选择OD对中旅行费用最短的超路径作为出行方案. 满足用户均衡条件的公交分配问题可以描述为两种的变分不等形式（variational inequality，VI）问题，分别为[10,15]

VI 1：

此外，对于每一对起讫点，存在多种出行策略，即多条超路径. 特别当有多条线路时会存在多种策略，但策略之间存在一定的关联性.

式中：C12、C3、C123分别为{1，2}、{3}、{1，2，3}的费用.

图4 公交线路共线及出行策略Fig. 4 Bus common line and travel strategies

因为有C12= C3，化简可得

若比较C123与C3，化简后只需比较与的大小；两边同时乘以，左边为同时得到右边为. 故，{1，2，3}比{1，2}和{3}有更低的费用. 类似地，{1，2，3}和{1}同时为最优策略，则此时{2}，{3}和{2，3}不可能为最优策略. 借助策略之间的联系就可以排除一些策略.

2 公交分配问题的敏感度分析

2.1 敏感度分析的解析表达式

根据已有文献[16-17]，在VI 1的扰动问题中引入扰动向量，当其任意最优超路径流量解为时，结合 K-T （Kuhn-Tucker）条件，扰动问题为

这一简化变换等价于在代数空间中将非基变量的相应约束移除，因此首要工作就是在矩阵中找到最大线性无关组[16]. 通过选择最大线性无关的超路径组合，可得

此时，可以将隐函数存在定理应用于上述受限制的系统中. 在的邻域内，将式（16）分别对、求导，得

进一步整理得

至此，推导了VI 1扰动问题的敏感度表达式.

2.2 敏感度结果的应用

2.2.1 评价指标

网络总体性能评价指标通常用来描述网络的性能状况. 常见的指标有：总旅行费用、总旅行时间、客运周转量、线路负荷[18-20].

式中：lij、qij分别为线路上站点i，j之间的线路长度、客流量；Ts为线路运营时间，h.

2.2.2 关键参数识别

模型的精度取决于输入和参数的精度，因此需要准确地对模型参数进行标定和校验，但这通常需要大量的工作. 由于可用资源有限，通过计算总旅行费用关于特定参数的偏导数信息来识别关键参数，可以更好地抓住重点，简化工作. 其次，相关偏导数信息可用于进行交通控制、不确定分析、悖论分析等方面的研究.

本文主要进行了关键参数识别的工作，然后结合实例将这些偏导数信息应用于交通控制，并在实际情形中提出改善现状的相关措施. 为便于表示，令 T 为总旅行费用，T 对中各参数的偏导如式（24）～（28）所示.

2.2.3 距离感知参数取值分析

在第3节中分析距离敏感程度d对于流量分配结果的影响，以及产生的相关影响.

3 实例应用分析

3.1 参数定义

为了分析考虑距离影响下的公交网络的性能状况，现以一个简单的实例进行说明. 简单公交网络如图5所示，包含了7条公交线路，图中，O、D分别为起、讫点，A、B、C为中间公交站点，弧段上方的时间为车内旅行弧段的零流时间，线路频率为车头时距的倒数.

图5 简单公交网络Fig. 5 Simple transit network

通过1.1节得到扩展的公交网络示意见图6.图6中数字为相应弧段编号，共计24条弧段；O1～O3为 O的扩展站点，A3为 A的扩展站点，B1～B2为B的扩展站点，C3～C6为C的扩展站点，D1、D4～D6为D的扩展站点. 本文为简化研究，不考虑步行弧段，且规定下车弧段的费用为0. 弧段中费用函数的参数取值见表1.

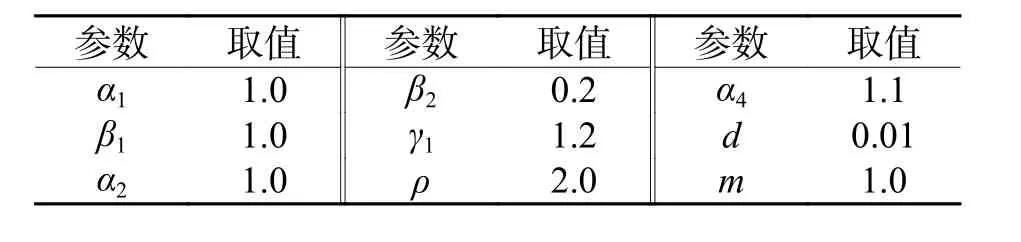
由此，得到弧段费用为

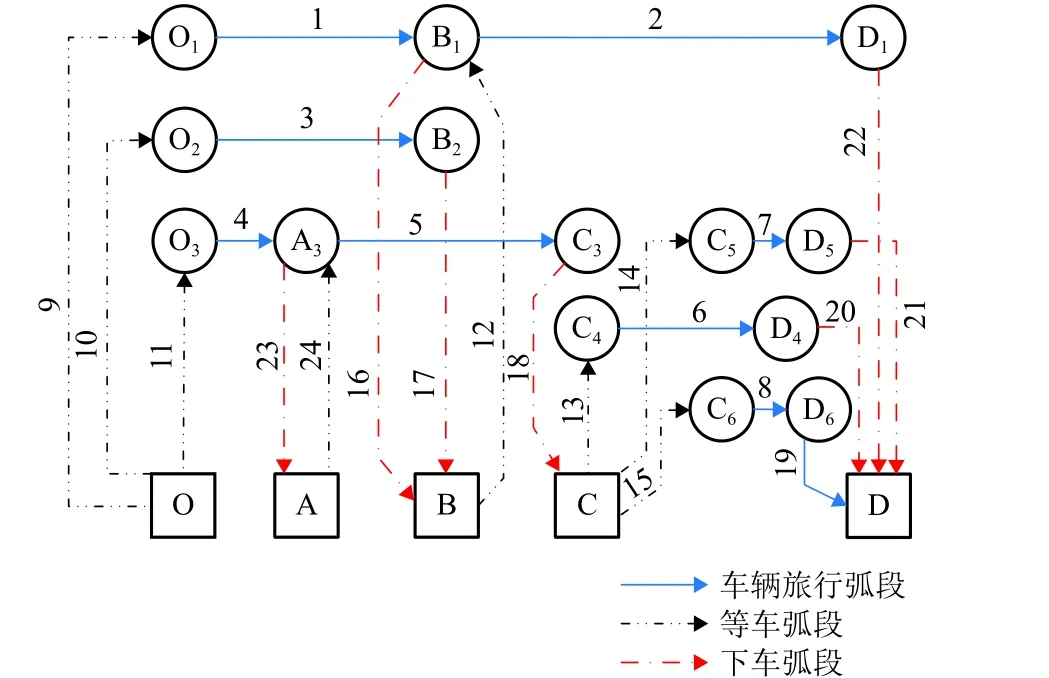
图6 扩展的公交网络示意Fig. 6 Expansion diagram of transit network

images/BZ_147_1271_1771_2196_1958.png

3.2 考虑距离影响的超路径费用分析

根据图5网络，首先在局部范围对C—D两点间的选择行为进行对比分析. 情形1：不考虑距离影响的超路径费用，情形2：考虑距离影响的超路径费用. C—D间有3条不同的公交线路，根据超路径理论得7种策略. 策略1～3分别对应3条简单路径；策略4～7分别为策略1～3的组合.

1）策略 1 （H1）： C→C4→D4→D；

2）策略 2 （H2）： C→C5→D5→D；

3）策略 3 （H3）： C→C6→D6→D；

4）策略 4 （H12）： {策略 1，策略 2}；

5）策略 5 （H13）： {策略 1，策略 3}；

6）策略 6 （H23）： {策略 2，策略 3}；

7）策略 7 （H123）： {策略 1，策略 2，策略 3}.

进一步可以得到

为寻找最短路径，探究其在不同需求水平下均衡分配时超路径费用的情况，分别讨论情形1和情形2时的状况，见图7.

图7 超路径广义费用情况Fig. 7 Generalized cost of hyperpaths

令C—D之间的需求从0增加至1 000人/h. 对比情形1和情形2发现：情形2中，在点（459.535 9，17.600 0）处，策略5和策略7的费用函数相交，此后随需求增加，这两种策略对应的超路径费用一直相等. 从网络分配的角度解释：在该点之前，策略5是最优策略，需求量全部加载在上面；当刚好达到该点时，次优策略7上升为最优策略，而其他的策略因为超路径费用高于最小费用而没有被采用，符合Wardrop第一原理. 但在情形1中，策略5和策略7的费用始终相等且为最小. 这说明在均衡条件下，网络中会同时存在多条被使用的超路径. 并且，是否考虑距离影响因素，在实际的规划中会导致流量分配出现一定的差异. 因此需要关注距离的影响作用.

3.3 关键参数分析

将上述方法应用于图6网络进行流量分配. 假定O—D之间的需求为1 000人/h. 计算得到均衡状态下存在两条超被使用的路径OD1和OD2，流量分别为hOD1= 913.107 4和hOD2= 86.892 6，其他超路径流量均为0. 具体地，超路径OD1为{O→O1→B1→D1→D，O→O2→B2→D1→D，O→O3→A3→C3→C5→D5→D，O→O3→A3→C3→C6→D6→D}，超路径 OD2为{O→O1→B1→→D1→D，O→ O2→B2→D1→D，O→O3→A3→C3→C4→D4→D， O→O3→A3→C3→C5→D5→D}. 此时得到车内旅行弧段流量解向量为V=（285.714 3，642.857 1，357.142 9，357.142 9，357.142 9，17.733 2，208.965 8，130.443 9），并求得使用超路径中旅行弧段-超路径的邻接矩阵和OD-超路径关联矩阵，且为线性无关[16].

通常模型中都存在一些不确定的参数，如本文中的d，需要根据实际情况进行标定并校正. 如果标定的不合理将会使模型的精度降低，无法达到预期效果. 因此，有必要对于这些参数进行分析，识别出关键参数，并进行较为准确的标定校正. 本文选取d、ρ、α1和Cbus进行分析，根据式（24）～（27），得到T关于这4种参数的偏导数信息，见表2.

表2 T对于不同参数偏导数值Tab. 2 Derivatives of T with respect to different parameters

从表 2 中看到，相较于 ρ 、Cbus，参数d、 α1的精度对于模型输出更为重要，也就是当d和 α1发生扰动时，对模型求解得到的均衡流量解的影响更大. 计算发现T对的偏导为负数，这说明在图6网络需求较小时，理论上加大公交车车型来提高最大容量能够减少总旅行费用. 因为车内拥挤效应下降，从而感知阻抗值变小. 此外，d相较于对于总旅行费用的影响更大. 也就是说，距离因素的影响最大. 因此，如何较好的度量感知作用对于模型输出结果的可信度有很大影响. 下一阶段将对d的取值做进一步分析.

3.4 d取值分析

参数d的大小反映了出行者对于距离的敏感程度.在3.3节的关键参数分析中，两条超路径OD1和OD2的重叠程度比较高. 在OD需求为1 000～1 500人/h的范围内，选择策略不变. 基于此，根据式（28），分析了在弧段7中考虑距离影响下，T关于f7的偏导数信息见图8.

图8中，偏导数取正值，表示提高公交线路7的发车频率，总旅行费用将增加；偏导数取负值，表示提高频率总旅行费用反而减少. 当偏导数为正时，认为是不利情况，因为原本通过增加频率来提高公交线路的服务水平，但结果却增加了出行者的总旅行费用. 随着参数d的取值增大，这种不利情况逐渐消失，并且达到图8中的T可降低区域，即通过增加发车频率来提高服务水平，从而缓解拥挤并减少总旅行费用.

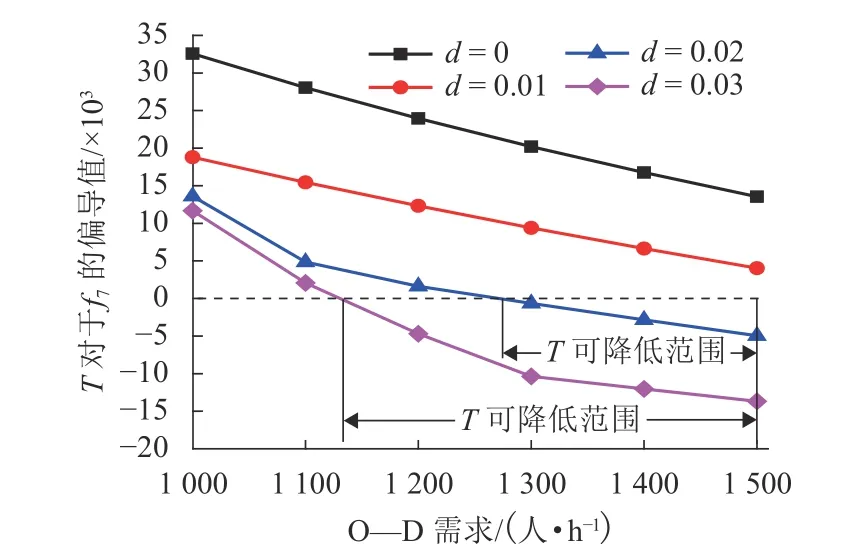
图8 距离敏感度的影响Fig. 8 Influence of distance sensitivity

当需求为1 500人/h时，分析弧段5～7的情况.弧段流量和T关于线路发车频率的偏导数信息见表3. 整体而言：参数d取0和0.02时，流量关于频率的偏导数值正负性相同，数值上有着略微差别；在数值变化上，流量关于f5偏导数的改变量相较于f6与f7更大，即线路5上流量的改变关于d更加敏感. 据此可以寻找到网络中那些关于d较为敏感的线路，实现分级别管理. 此外，考虑距离影响会改变T可降低区域的范围，表3中T可降低数值已加粗.特别的，T关于f7的偏导数在d= 0时为正值，d=0.02时为负值，也就是说在d= 0.02时提高f7可作为降低T的一种方式，这为决策者灵活地制定公交优化方案提供了有效途径. 同样地，考虑距离参数d可为寻找其他网络性能指标（如总周转量、总旅行时间等）的优化目标范围提供理论支持，修正因未考虑距离影响带来的分析误差，为管理者的决策提供相应依据.