用于单电感双输出Buck变换器的PCPV控制方案

徐利梅 ，王 瑶 ，张留洋 ，杨甲勇

（西南民族大学电气工程学院，四川 成都 610041）

多输出开关DC-DC变换器主要应用于驱动具有不同电源需求的负载. 传统多输出开关DC-DC变换器由多个单输出开关DC-DC变换器并联构成，需要多个电感和开关管. 随着便携式电子产品和LED照明技术的快速发展，其对供电电源的体积和成本要求越来越高[1-2]. 单电感多输出（single-inductor multiple-output，SIMO） DC-DC变换器通过一个电感实现多路输出，减小了电源体积、节约了制作成本[3-4]，为多路电源需求的负载提供了一个较好的解决方案. 然而，SIMO DC-DC变换器多个输出支路共用一个电感[5-7]，一条输出支路负载变化时会引起电感电流发生变化，从而引起其它支路的输出发生变化，产生交叉影响[8]. 近年来，许多文献围绕SIMO DC-DC变换器的交叉影响问题进行了研究，提出了有效的解决方案.

文献[9-11]采用的分时复用方法消除了单电感双输出（single-inductor dual-output，SIDO）DC-DC变换器的交叉影响. 但该方法仅对工作于断续导通模式（discontinue conduction mode，DCM）和伪连续导电模式（pseudo-continue conduction mode，PCCM）的SIDO DC-DC变换器有效. 由于SIDO DCM DC-DC变换器电流、电压纹波较大和SIDO PCCM DC-DC变换器效率较低等问题，在交叉影响能够得到有效抑制的前提下，通常选用工作于连续导电模式（continue conduction mode，CCM）的SIDO DC-DC变换器.

文献[12-15]采用解耦控制方法减小了SIDO CCM DC-DC变换器的交叉影响. 文献[12]对控制-输出传递函数进行解耦控制，减小了交叉影响；文献[13]通过交叉引入输出状态变量的导数，直接对变换器的交叉影响传递函数进行解耦控制，大大减小了交叉影响；基于文献[13]，文献[14]通过交叉引入输出电流对交叉影响传递函数进行补偿，进一步减小了交叉影响；文献[15]提出基于H∞理论的多变量控制方法来实现交叉影响传递函数的解耦控制，从而在理论上消除了交叉影响. 解耦控制方法对交叉影响的抑制十分有效，但计算复杂，且实际实现时较为困难.

第三类能够有效抑制交叉影响的方法为纹波控制方法[16-18]. 文献[16]中，基于电流纹波的共模-差模控制方法具有快速的负载瞬态响应速度，从而减小了交叉影响；文献[17]采用峰值电流控制（peak current mode，PCM）方法，同样通过提高变换器负载瞬态响应速度的方法来减小交叉影响；在此基础上，文献[18]提出了电容电流控制方法，对SIDO CCM Buck变换器的输出交叉影响起到了很好的抑制效果. 相比解耦控制方法，纹波控制方法不但能有效地减小交叉影响，且控制电路简单易实现.

传统PCM控制SIDO Buck变换器的控制电路由两个峰值电流控制电路构成，峰值电流控制电路采样电感电流作为反馈量. 相比电感电流，电容电压（输出电压）能更快地反映负载变化，从而减小交叉影响. 因此，本文在PCM控制SIDO Buck变换器的基础上，引入输出电压纹波至控制电路，提出了峰值电流-峰值电压（peak-current and peak-voltage，PCPV）控制SIDO Buck变换器. 首先，分析了其电路结构、工作原理以及输出电压与输入电压的增益表达式；其次，建立了其状态空间平均模型和小信号模型，通过bode图对比分析了PCPV控制SIDO Buck变换器与PCM控制SIDO Buck变换器的输出交叉影响；最后建立了PCPV控制SIDO Buck变换器的实验电路，实验结果验证理论分析的正确性.

1 PCPV控制SIDO Buck变换器

1.1 电路结构

图1所示为PCPV控制SIDO Buck变换器的原理图，其中，图1（a）为SIDO Buck变换器原理，图 1（b）为 PCPV 控制电路原理. 如图 1（a）所示，SIDO Buck变换器由输入电压源vi、开关管S1和S2、电感L、二极管D1和D2、电容C1和C2、及电阻负载R1和R2组成. vi通过L储存和释放能量，得到两路输出电压v1、v2和输出电流i1、i2. 为减少开关管的数量，实现 D2与 S1互补导通，要求 v1＜ v2，并定义 v1、v2的输出支路分别为输出支路1和输出支路2. 如图1（b）所示，PCPV控制电路包括峰值电流控制电路和峰值电压控制电路，由运算放大器AM1和AM2、PI (proportional integral) 调节器 PI1和 PI2、比较器CM1和 CM2、RS 触发器 RS1和 RS2、采样电阻 rs及时钟信号clk构成.

图1 PCPV控制SIDO Buck变换器原理Fig. 1 Schematic diagram of PCPV-controlled SIDO Buck converter

峰值电流控制电路由电压控制外环和电流控制内环组成，峰值电压控制电路由电压控制外环和电压控制内环组成. 在峰值电压控制电路中，电压控制外环采样v1与基准电压Vref1作差，得到误差电压ve1，ve1通过PI1得到放大的误差电压vm1作为电压控制内环的参考电压；同时，电压控制内环采样v1，v1与vm1通过CM1比较，比较结果作为RS1的R端的输入信号，clk作为RS1的S端的输入信号，RS1的Q端输出控制信号vg1控制S1. 在峰值电流控制电路中，电压控制外环采样v2与基准电压Vref2作差，得到误差电压ve2，ve2通过PI2得到放大的误差电压vm2作为电流控制内环的参考电流；电流控制内环通过rs得到采样，rsiL与vm2通过CM2比较，比较结果和时钟信号clk分别作为RS2的R端和S端的输入信号，RS2的Q端输出控制信号vg2控制S2.需要说明的是，本文仅对输出支路1的控制电路引入了电容电压（输出电压）纹波，因此仅能减小输出支路2对输出支路1的交叉影响.

1.2 工作原理

图2所示为PCPV控制SIDO Buck变换器工作于CCM的控制时序图，结合图1所示电路原理，PCPV控制SIDO Buck变换器的工作原理描述如下：

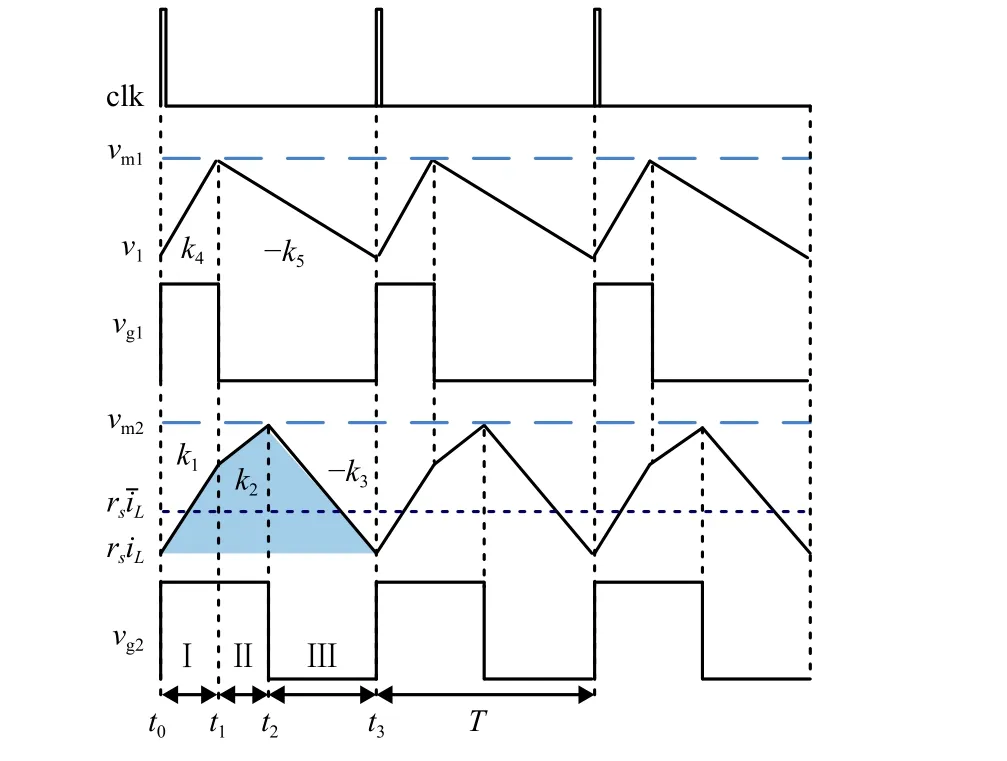
图2 PCPV控制SIDO Buck变换器控制时序Fig. 2 Control timing of PCPV-controlled SIDO Buck converter

在开关周期的起始时刻，clk使S1和S2导通，则D1和D2关断；vi为L充电，rsiL以斜率k1线性上升；同时vi为R1供电，v1以斜率k4线性上升；C2为R2供电.

当v1上升至vm1，S1关断，D2导通，S2保持导通，D1保持关断；vi继续为L充电，且为R2供电，rsiL以斜率k2继续线性上升；C1为R1供电，v1以斜率 -k5线性下降.

当rsiL上升至vm2，S2关断，D1导通，S1保持关断，D2保持导通；L为R2和C2供电，rsiL以斜率-k3线性下降；C1继续为R1供电，v1以 -k5继续线性下降，直至下一个时钟周期到来.

k1～k5、vm1和vm2的表达式分别如下：

式中：kp1和kp2分别PI1和PI2的比例系数；ki1和ki2分别为PI1和PI2的积分系数.

通过上述分析可知，在图2控制时序下，一个开关周期T内，PCPV控制SIDO Buck变换器存在3种工作模态：开关周期起始时刻至v1上升至vm1时，即[0，d1T]工作区间为工作模态Ⅰ；工作模态Ⅰ结束时刻至 rsiL上升至 vm2时，即[d1T，（d2-d1）T]工作区间为工作模态Ⅱ；工作模态Ⅱ结束时刻至rsiL下降至开关周期结束时刻时，即[（d2-d1）T，（1-d2）T]工作区间为工作模态Ⅲ. 图2中，为rsiL的纹波波形中阴影部分的平均值.

1.3 电压增益

令L两端电压为vL，其在工作模态Ⅰ～Ⅲ的表达式分别为vi-v1、vi-v2和 -v2. 由电感伏秒平衡原理可知：一个稳态开关周期内，vL的平均值等于0. 由此可得

式中：d1、d2分别为 S1、S2的占空比.

令流过C1的电流为，其在工作模态Ⅰ～Ⅲ的表达式分别为 iL-i1、-i1和-i1，其中输出电流 i1=v1/R1. 由电容安秒平衡原理可知：一个稳态开关周期内，ic1的平均值等于0. 由此可得

对于SIDO Buck变换器，在一个稳态周期内，电感电流平均值等于输出电流平均值，即

联立式（5）～（7）可得PCPV控制SIDO Buck变换器v1、v2与vi的增益表达式分别为

根据式（8）、（9）和已知电路参数，可确定 d1和d2的大小.

2 小信号建模与分析

PCPV控制SIDO Buck变换器由SIDO Buck变换器和PCPV控制两部分组成，本节分别对这两部分进行小信号建模，从而得到PCPV控制SIDO Buck变换器的小信号模型. 在此基础上，对变换器的交叉影响进行对比分析.

2.1 SIDO Buck变换器小信号建模

选取 iL、v1和v2为状态变量，令状态变量向量基于1.2节工作原理的描述，得到PCPV控制SIDO Buck变换器的工作模态Ⅰ、工作模态Ⅱ和工作模态Ⅲ的状态方程为

式中：

基于式（10），采用状态空间平均方法，得到SIDO Buck变换器的状态空间平均模型为

式中：s为拉普拉斯变换中的复变量.

2.2 PCPV控制小信号建模

由图2中v1的纹波波形可知

2.3 交叉影响分析

根据式（12）、（14）和（19）得到 PCPV控制SIDO Buck变换器的小信号模型如图3所示，进而对PCPV控制SIDO Buck变换器的输出交叉影响进行分析.

记PCPV控制SIDO Buck变换器输出支路1对输出支路2的交叉影响传递函数为输出支路2对输出支路1的交叉影响传递函数为基于图3所示小信号模型，采用表1所示电路参数，得到交叉影响传递函数z12(s)和z21(s)的 bode图分别如图 4（a）和 4（b）所示.

图3 PCPV控制SIDO Buck变换器小信号模型Fig. 3 Small signal model of PCPV-controlled SIDO Buck converter

表1 PCPV控制SIDO Buck converter电路参数Tab. 1 Circuit parameters of PCPV-controlled SIDO Buck converter

图4中，黑色虚线代表PCM控制SIDO Buck变换器的交叉影响传递函数的幅频曲线与相频曲线，蓝色实线代表PCPV控制SIDO Buck变换器的交叉影响传递函数的幅频曲线与相频曲线. 从图4（a）中看出，与PCM控制SIDO Buck变换器相比，PCPV控制SIDO Buck变换器的交叉影响传递函数z12(s)的幅频曲线的低频增益大小相近，说明两种变换器的输出支路1对输出支路2的交叉影响大小差异不大. 从图 4（b）中看出，PCPV控制 SIDO Buck变换器的交叉影响传递函数z21(s)的幅频曲线的低频增益更小，说明PCM控制SIDO Buck变换器输出支路2对输出支路1的交叉影响大于本文提出的PCPV控制SIDO Buck变换器，即输出支路2中的负载电流跳变时，PCM控制SIDO Buck变换器相比于PCPV控制SIDO Buck变换器会在输出支路1的输出电压中引起更大的幅值响应. 由此说明：相比PCM控制SIDO Buck变换器，PCPV控制SIDO Buck变换器减小了输出支路2对输出支路1的交叉影响.

图4 PCM和PCPV控制SIDO Buck变换器的交叉影响传递函数bode图Fig. 4 Bode diagram of cross regulation transfer function of PCM and PCPV-controlled SIDO Buck converter

3 实验验证

为验证理论分析的正确性，搭建了PCPV控制SIDO Buck变换器的实验电路，实验参数同表1.PCPV控制SIDO Buck变换器的实验电路如图5所示，得到的验证原理和交叉影响的稳态实验波形和瞬态实验波形如图6和图7所示.

3.1 稳态实验波形

图6所示为PCPV控制SIDO Buck变换器工作于稳态时的主要实验波形. 其中，图6（a）为iL、d1和d2的实验波形；图 6（b）为vi、v1和v2的实验波形. 从图6可知：vg1大于vg2，一个开关周期内，iL先上升两次再下降一次；且vi为10 V时，v1和v2分别为3.3 V和5.0 V. 实验结果与工作原理相符，且验证了控制方法的可行性.

图5 PCPV控制SIDO Buck变换器实验电路Fig. 5 Experimental prototype of PCPV-controlled SIDO Buck converter

图6 PCPV控制SIDO Buck变换器稳态实验波形Fig. 6 Steady-state experimental waveforms of PCPV-controlled SIDO buck converter

3.2 瞬态实验波形

图7 所示为负载变化时，PCM控制和PCPV控制SIDO Buck变换器的瞬态实验波形. 其中，图7（a）和图7（b）分别为PCM控制和PCPV控制SIDO Buck变换器的输出支路1负载变化时，i1、v1和v2的瞬态实验波形. 图 7（c）和图 7（d）分别为 PCM 控制和PCPV控制SIDO Buck变换器的输出支路2负载变化时，输出电流i2、v1和v2的瞬态实验波形.

图7 PCM控制和PCPV控制SIDO Buck变换器的瞬态实验波形Fig. 7 Transient experimental waveforms of PCM-controlled and PCPV-controlled SIDO buck converter

由图 7（a）和图 7（b）可知，i1从 1.0 A 突变至1.5 A时，PCM控制SIDO Buck变换器的v1经过约12.5 ms的调整时间进入了新的稳态；PCPV控制SIDO Buck变换器的v1经过几个开关周期的调整时间便进入了新的稳态，提高了变换器的瞬态性能.PCM控制和PCPV控制SIDO Buck变换器的v2在瞬态调整过程中，最大电压变化量均约600 mV，即输出支路1对输出支路2的交叉影响均约600 mV，说明PCPV控制与PCM控制SIDO Buck变换器输出支路1对输出支路2的交叉影响大小差不多.

从图7（c）可以看出，i2从2.0 A突变至2.5 A时，PCM控制SIDO Buck变换器的v2经过约12.5 ms的调整时间进入了新的稳态；输出支路2对输出支路1的交叉影响为300 mV. 从图7（d）可以看出，在与图7（c）相同负载变化情况下，PCPV控制SIDO Buck变换器的v2经过约10.0 ms的调整时间进入了新的稳态；输出支路2对输出支路1几乎无交叉影响. 由此说明：相比于传统PCM控制SIDO Buck变换器，本文所提出的PCPV控制SIDO Buck变换器极大地改善了输出支路2对输出支路1的交叉影响，且提高了变换器的瞬态性能. 实验结果与理论分析结果相符.

4 结 论

本文提出了PCPV控制SIDO Buck变换器，以减小输出支路间的交叉影响. 首先，介绍了其电路结构和工作原理；采用电感伏秒平衡和电容安秒平衡原理，推导了输出电压与输入电压的增益表达式. 然后，基于状态空间平均方法，建立了PCPV控制SIDO Buck变换器的状态空间平均模型和小信号模型. 最后，通过bode图分析和实验验证，与传统PCM控制SIDO Buck变换器对比分析了交叉影响的大小，得到以下结论：

1） 输出电流i1变化时，PCPV控制SIDO Buck变换器与PCM控制SIDO Buck变换器的输出支路1对输出支路2的交叉影响差异小；

2） 输出电流i2变化时，相比于PCM控制SIDO Buck变换器，PCPV控制SIDO Buck变换器有效地减小了输出支路2对输出支路1的交叉影响；

3） PCPV控制SIDO Buck变换器的负载瞬态性能更好.