一阶微分方程的积分因子研究

安 然,田十方,刘晓薇

齐鲁工业大学(山东省科学院) 数学与统计学院,济南 250353

常微分方程是一个有着长期历史而又不断发展的学科,不仅具有理论研究意义而且有实际应用价值,得力于其他数学分支的支持,也为其他数学分支服务,促进了时代的发展进步。

积分因子概念是由瑞士大数学家欧拉(Euler)提出来的,他还确定了采用积分因子方法的微分方程类型,证明了只要是可用变量分离求解的微分方程都可以用积分因子进行求解,但是反之不然。随着微分方程理论的不断深入研究和探索,积分因子的应用越来越广泛。经过许多科学家的研究证明,不仅仅是分离变量求解的微分方程可以用积分因子法求解,甚至只要微分方程的解存在都可以采用积分因子法求解,只是有些方程求积分因子比求方程的解本身更为复杂。目前国内学者寸得偶、潘鹤鸣等分别对积分因子的求法作了比较详细的研究[1]。本文在前人研究的基础上,给出了一些微分方程存在某些特殊类型积分因子的求解方法。

1 常微分方程的基本概念

1.1 问题准备

定义1: 将自变量、未知函数和其导数联系在一起的关系式称为微分方程。若这种微分方程自变量的个数只有一个,称为常微分方程[2]。例如:xdy-y2dx=0。

定义2 : 考虑对称形式的微分方程

M(x,y)dx+N(x,y)dy=0,

(1)

如果存在一个可微函数u(x,y),使得它的全微分为

du(x,y)=M(x,y)dx+N(x,y)dy,

(2)

亦即它的偏导数

则称(1)为恰当方程或全微分方程。

定义3: 若方程(1)不满足恰当方程的条件,但是方程(1)两端乘以一个非零的函数μ(x,y)后能成为一个恰当微分方程,这样的函数μ(x,y)称为方程(1)的积分因子。

(注:可以证明,微分方程只要解存在,那么积分因子一定存在,而且不是唯一的。)

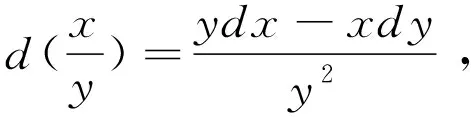
1.2 关于恰当方程求解的一般方法

定理1:若M(x,y),N(x,y)在某个单连通区域上连续,而且具有一阶连续的偏导数,那么方程(1)是恰当方程的充要条件是:

(3)

显然,恰当方程的通解为u(x,y)=c,c为任意常数。恰当方程可以通过积分

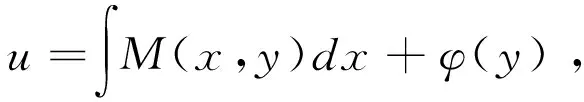
(4)

求其通解,这里的φ(y)是y的任意可微函数[4]。

2 几类特殊积分因子存在的充要条件

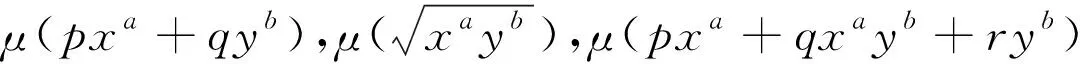
情形1:

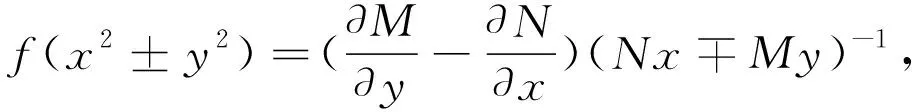
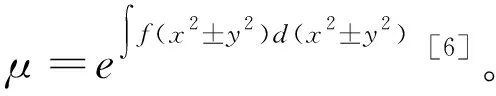
证明:一般函数μ(x,y)是积分因子的充要条件是

(5)

现若μ=μ(x2+y2)=μ(z)是积分因子,则

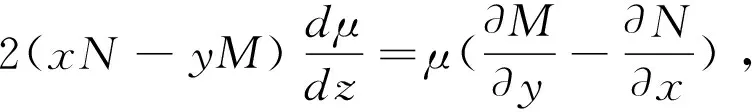
(6)

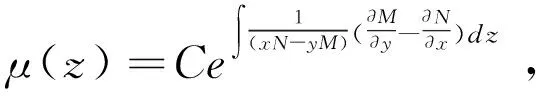
故要使方程有形如μ(x2+y2)的积分因子的充要条件是

同理,可证方程

M(x,y)dx+N(x,y)dy=0

有特殊积分因子μ=μ(x2-y2)的充要条件是

例:

求方程(x-y)dx+(x+y)dy=0的积分因子[7]。

解:因为

仅为z=x2+y2的函数,所以原方程有积分因子

推论1:

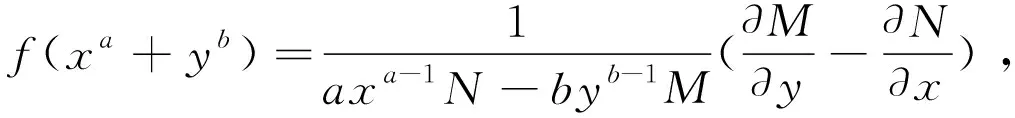
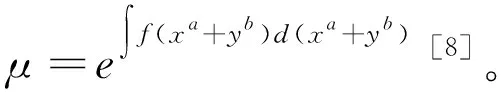
在推论1的基础上得到了推论2的结论,证明方法同情形1。

推论2:

方程M(x,y)dx+N(x,y)dy=0有特殊积分因子μ=μ(pxa+qyb)的充要条件是

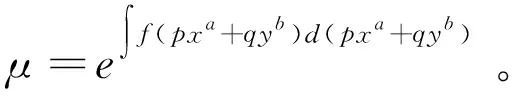
情形2:

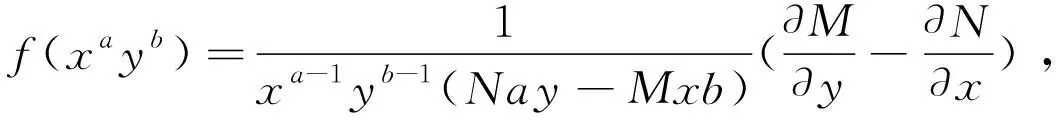
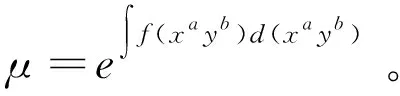
证明:一般函数μ(x,y)是积分因子的充要条件是

(7)

现若μ=μ(xayb)=μ(z)是积分因子,则

(8)

因此有

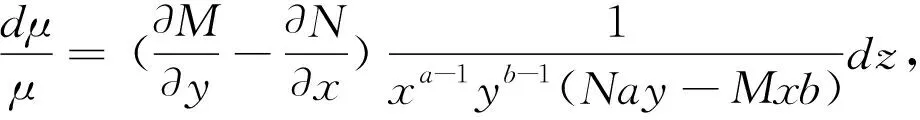
(9)

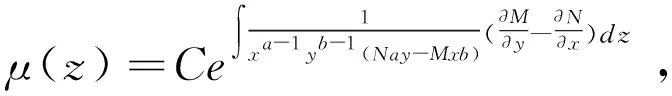
故要使方程有形如μ(xayb)的积分因子的充要条件是

是xayb的函数[9]。

在情形2的基础上,可以推导出推论3。

推论3:

情形3:

方程M(x,y)dx+N(x,y)dy=0有特殊积分因子μ=μ(pxa+qxayb+ryb)的充要条件是

f(pxa+qxayb+ryb)=

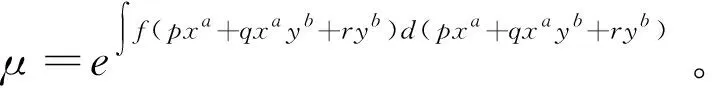
证明:一般函数μ(x,y)是积分因子的充要条件是

(10)

现若

μ(pxa+qxayb+ryb)=μ(z)

(11)

因此有

(12)

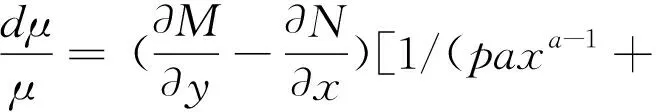
(13)

即

故要使方程有形如

μ=μ(pxa+qxayb+ryb)

的积分因子的充要条件是

是f(pxa+qxayb+ryb)的函数。

3 结束语

本文主要对一阶微分方程的积分因子的存在性进行研究。到今天,积分因子在一阶微分方程的求解中发挥了关键性作用。本文主要对非恰当微分方程转化为恰当微分方程的纽带——“积分因子”进行研究,介绍了几类特殊积分因子存在的充要条件,以后我们将持续关注积分因子在其他类型常微分方程中的作用,以及积分因子在证明等式等方面的应用。