汽油精制过程中的辛烷值损失预测模型

杜明洋,张甜甜,薄其高,许文文

齐鲁工业大学(山东省科学院) 数学与统计学院,济南 250353

目前,小型车辆的主要燃料是汽油,汽油燃烧排放的产物主要有一氧化碳、氮氧化合物、碳氢化合物、微粒等,对大气环境造成了重大影响。为此,世界各国都制定了日益严格的汽油质量标准。汽油清洁化重点是降低汽油中的硫、烯烃含量,同时尽量保持其辛烷值。为满足日益严格的清洁汽油标准不断降低硫和烯烃含量的需求,国内外在汽油清洁化领域开展了大量的研究工作。

辛烷值(RON)是反映汽油燃烧性能的最重要指标,目前除考虑改进发动机的构造和操作条件外,主要依靠提高汽油辛烷值,借以提高发动机压缩比的办法来增加功率和节约汽油。但是现有技术在对催化裂化汽油进行脱硫和降烯烃过程中,普遍降低了汽油辛烷值。辛烷值每降低1个单位,相当于损失约150元/吨。以一个100万吨/年催化裂化汽油精制装置为例,若能降低0.3个单位RON损失,其经济效益将达到4 500万元。因此降低汽油辛烷值损失具有重要意义。本文采用改进的因子分析法和随机森林算法建立汽油精制过程中的辛烷值损失预测模型。具体数据来源于某石化企业的催化裂化汽油精制脱硫装置运行4年所积累的历史数据[1-3]。

1 变量降维

在解决实际问题时,自变量过多对于模型的构建是弊大于利的,因此,一般采用先降维再建立模型的方法来简化模型。本文采用改进的因子分析法、随机森林两种方法分别对操作变量进行降维,最后比较两种方法的降维效果。

1.1 采用改进的因子分析降维

因子分析是将多个实测变量转换为少数几个综合指标(或称因子变量),它反映一种降维的思想。通过降维将相关性高的变量聚在一起,从而减少需要分析的变量的数量,降低问题分析的复杂性。因子变量满足以下特点:个数远远少于原始变量,但能反映原始变量的绝大部分信息。

因子分析的主要步骤为:

1)判断待分析因子变量是否适合进行因子分析。

2)构造因子变量并计算公因子方差。

3)利用旋转法使因子变量具有可解释性。

因子分析的数学模型为:

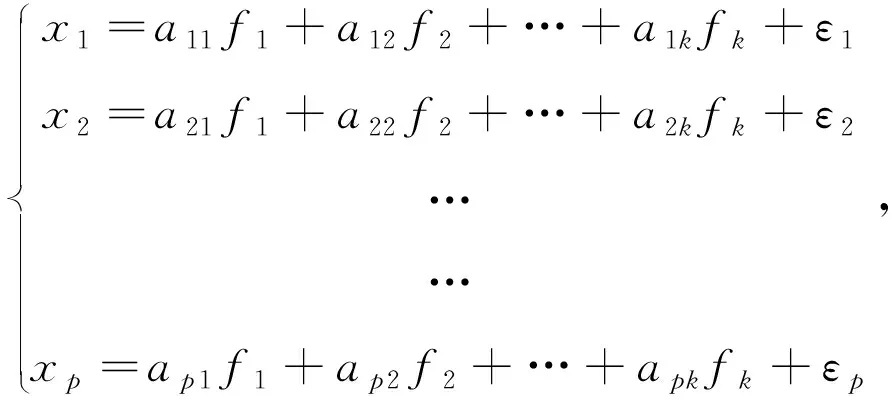
(1)

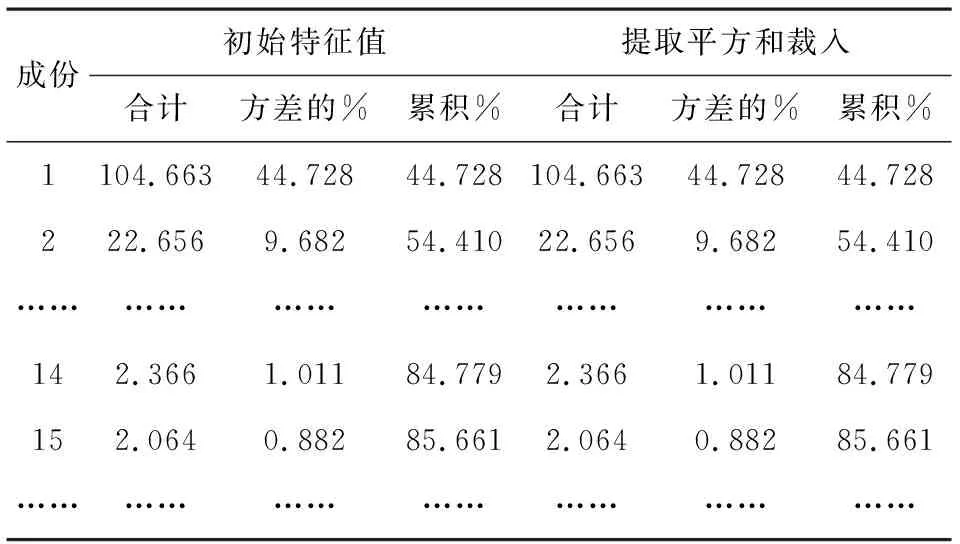
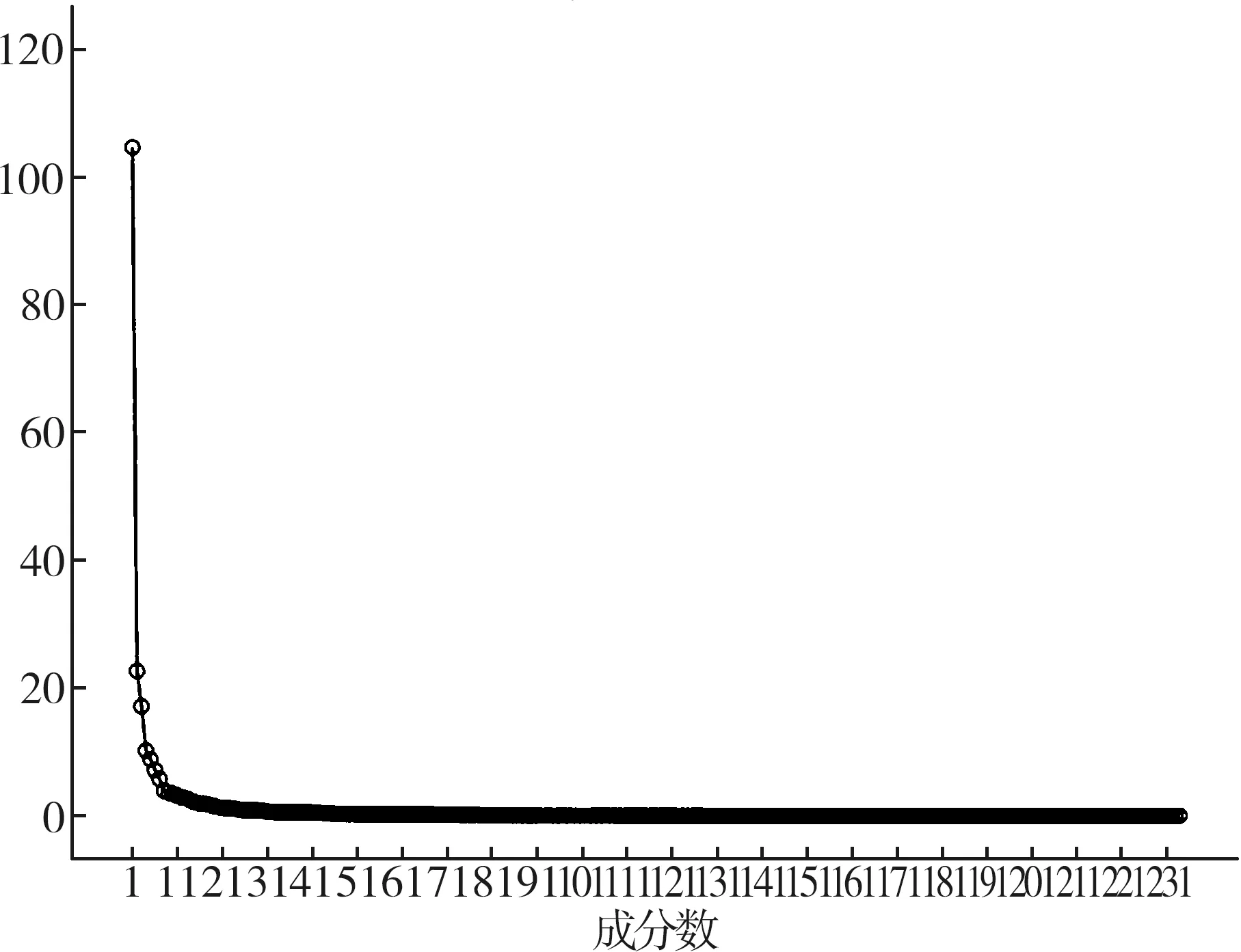
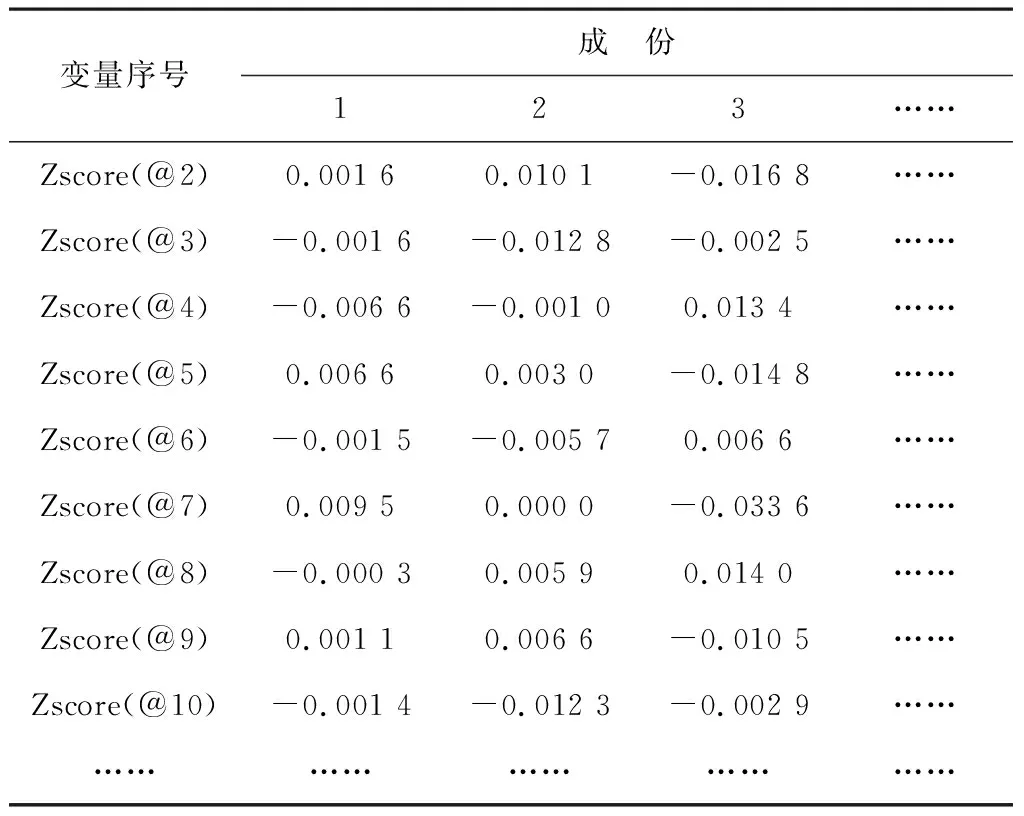
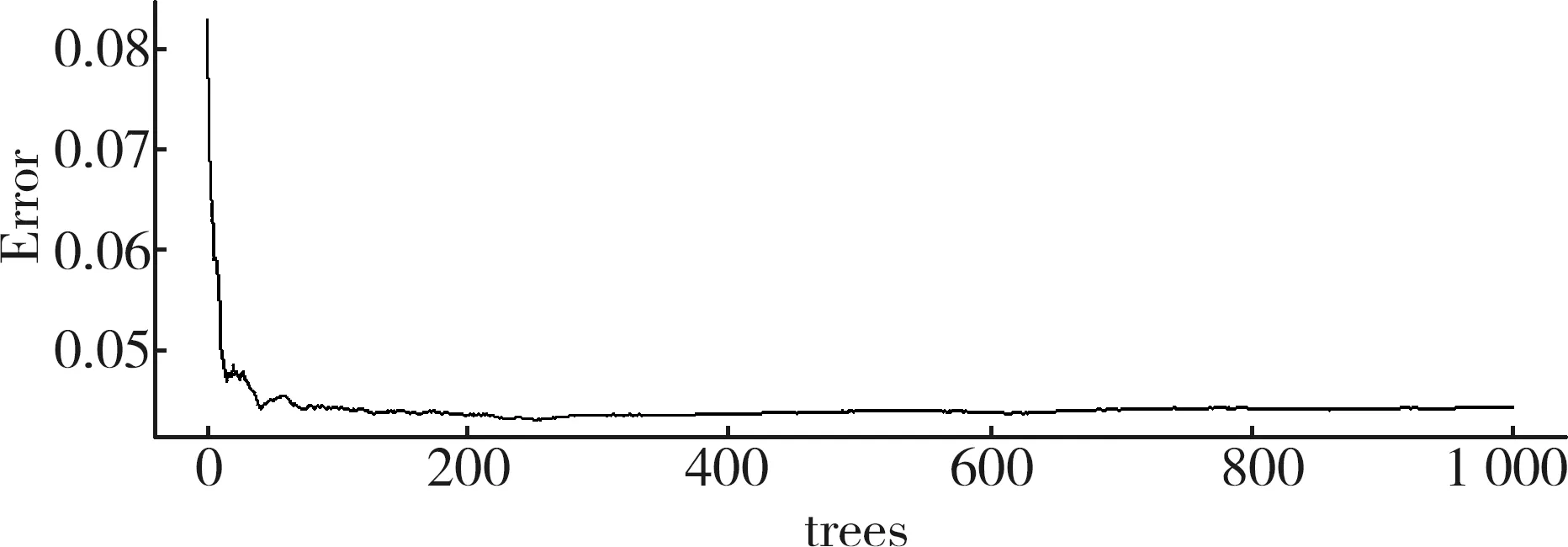
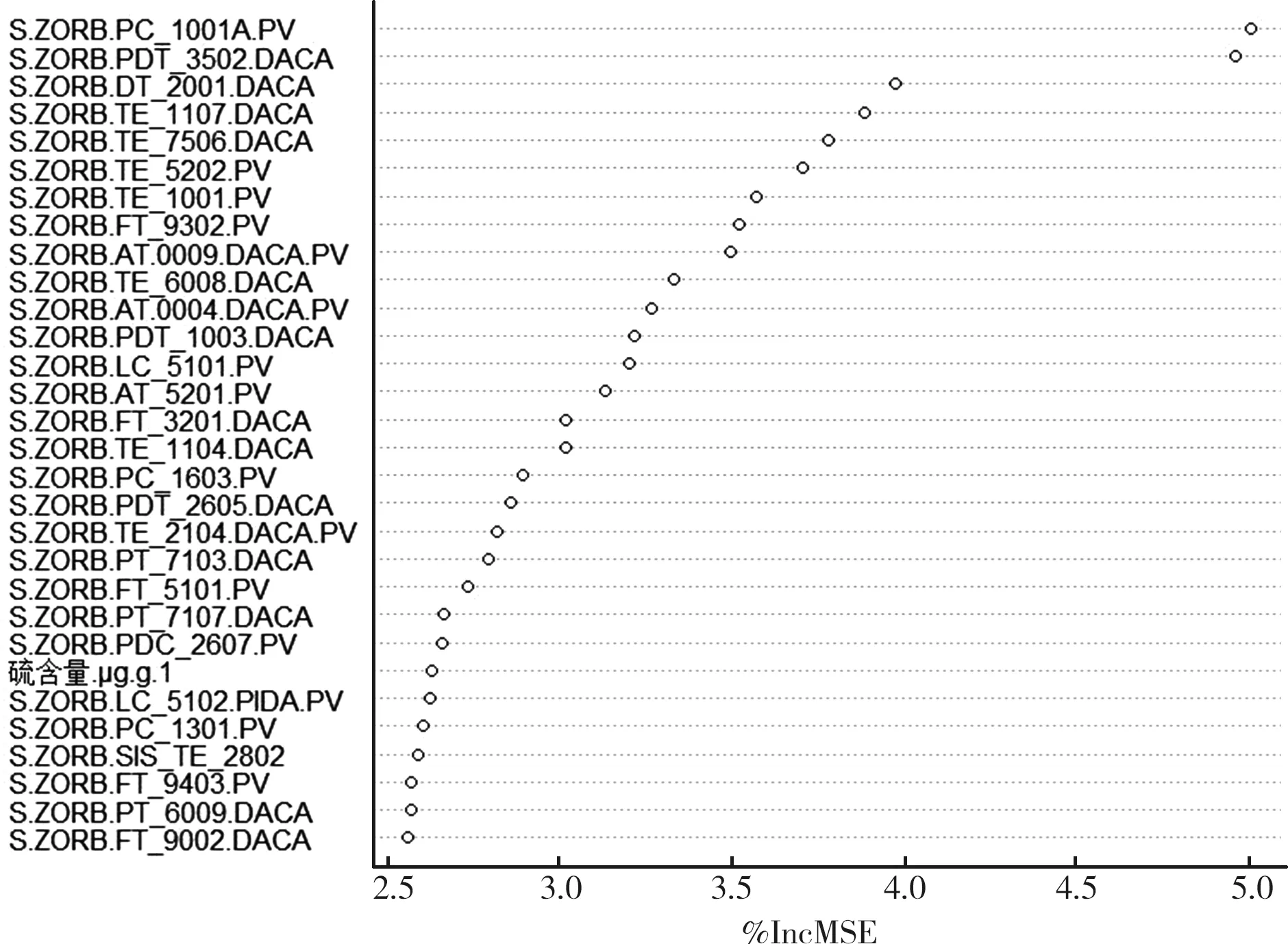
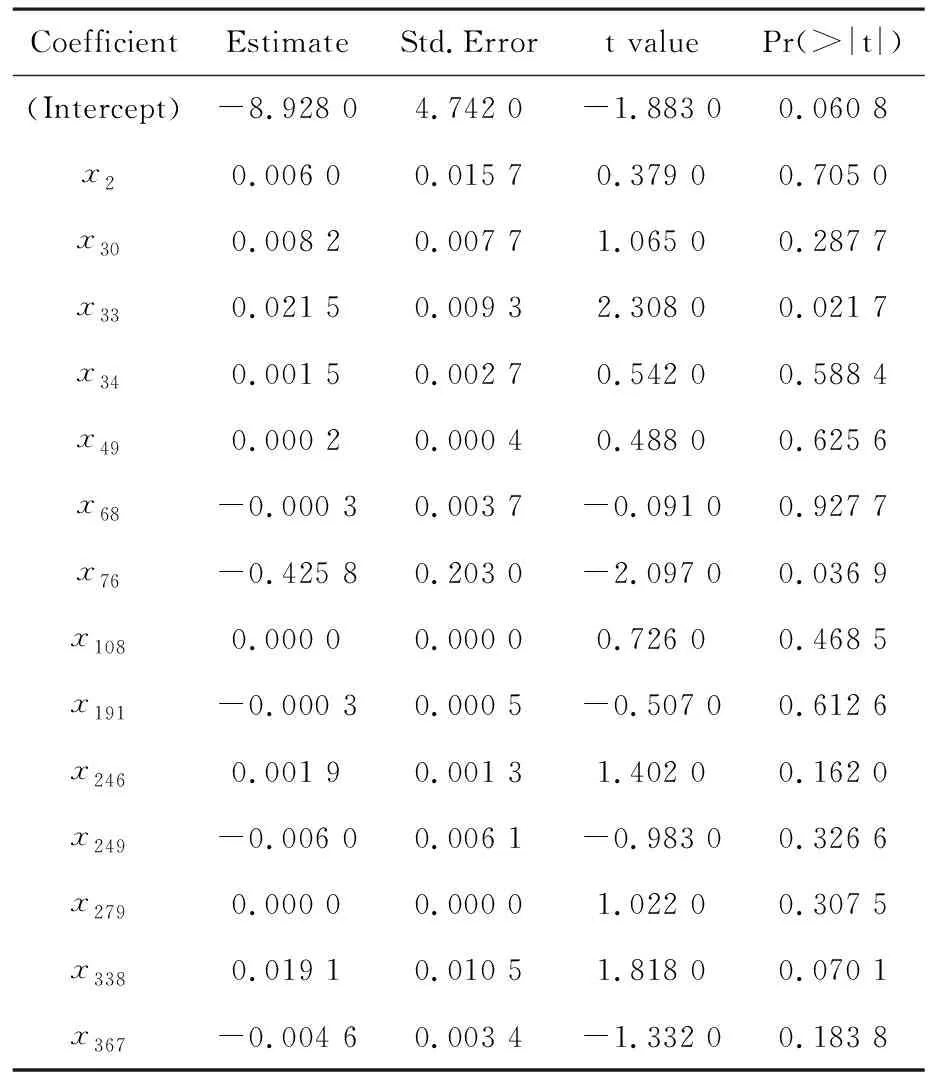
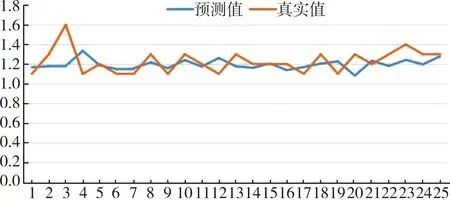
其中,xi为标准化后的原始变量,fi为因子变量,且k

上述模型也可用矩阵表示,即A=AF+ε,其中F为因子变量,A为载荷矩阵,aij为因子载荷,ε为特殊因子。所谓因子载荷,是指在因子变量不相关的情况下,第i个原始变量与第j个原始变量的相关系数,aij的绝对值越大,则xi与fi的相关性越强[4-5]。

将包括7个原料性质、2个待生吸附剂性质、2个再生吸附剂性质、2个产品性质以及另外354个操作变量(共367个变量)作为变量,RON损失作为因变量进行因子分析。将因变量和操作变量进行编号,令辛烷值损失为Y,367个变量编号依次为x1,x2,…,x367。

由于工业数据相对比较复杂,本文在传统因子分析的基础上,对原始操作变量与因变量进行相关性分析,分别计算原始操作变量与因变量之间的相关性,提取出与因变量相关性较强的变量,然后进行因子分析。此方法可以减少因子分析的工作量,同时提高降维效果,利用SPSS对原始数据进行分析处理。

1.1.1 提取公因子方差

每个操作变量均能通过公因子表达,但每个公因子可以表达原始数据信息的多少是通过公因子方差表的“提取”来表示的。利用SPSS得到公因子方差表,如表1。

表1 公因子方差

由上表可知,所有变量的提取值均大于0.7,说明这些变量都可以很好的被公因子表达,即分析结果比较理想,原始变量适合进行因子分析。

1.1.2 提取公因子

对预处理后的数据中原始操作变量与因变量进行相关性分析,得到相关性矩阵,将相关系数0.1作为标准,剔除相关性低于0.1的变量,共剔除133个变量。对保留的234个变量的数据进行因子分析,利用SPSS输出得到解释的总方差表如表2。

表2 改进的因子分析解释的总方差

将特征值大于1因子作为公因子,由表2可知,可提取14个公因子,其累计方差贡献率为84.779%,即这14个公因子可以解释84.779%的变量信息,原有变量的大多数信息能很好的被这14个公因子涵盖。输出的碎石图如图1。

图1 改进后的因子分析法碎石图

左侧斜率较大的部分代表特征值大,即成份1、成份2、…、成份14这14个成份包含大部分变量信息,提取这14个成份为公因子是可行的。

通过方差最大法获得正交旋转因子载荷矩阵,如表3。

表3 改进的因子分析旋转成分载荷矩阵

根据旋转成分矩阵可知,第1个公因子上具有较大载荷值的是原料性质中的辛烷值、S-ZORB.FT_9301.TOTAL、S-ZORB.FT_9201.TOTAL、S-ZORB.FT_9403.TOTAL和S-ZORB.FT_3301.TOTAL；第2个公因子上具有较大载荷值的是S-ZORB.FT_1503.TOTALIZERA.PV和S-ZORB.FT_1504.TOTALIZERA.PV；第3个公因子上具有较大载荷值的是S-ZORB.PT_5201.DACA；第4个公因子上具有较大载荷值的是S-ZORB.PDT_2703B.DACA和S-ZORB.PDI_2801.DACA；第5个公因子上具有较大载荷值的是S-ZORB.FT_1001.PV；第6个公因子上具有较大载荷值的是S-ZORB.FT_9102.PV；第7个公因子上具有较大载荷值的是S-ZORB.PT_2901.DACA；第8个公因子上具有较大载荷值的是S-ZORB.TE_7106B.DACA；第9个公因子上具有较大载荷值的是S-ZORB.TE_1102.DACA.PV；第10个公因子上具有较大载荷值的是S-ZORB.PDC_2702.DACA；第11个公因子上具有较大载荷值的是S-ZORB.PT_6005.DACA；第12个公因子上具有较大载荷值的是S-ZORB.FC_5103.DACA；第13个公因子上具有较大载荷值的是S-ZORB.FT_9001.PV；第14个公因子上具有较大载荷值的是S-ZORB.TC_3102.DACA。

因此,根据改进的因子分析法进行降维提取出的公因子的信息大致可以用这20个变量包含,将此降维结果命名为结果1。

1.2 采用随机森林算法降维

随机森林是随机的建立一个森林,森林由很多的决策树组成,随机森林的每一棵决策树之间没有关联。得到森林后,当有一个新的输入样本进入时,让森林中的每一棵决策树分别判断这个样本应该属于哪一类(对于分类算法),然后观察哪一类被选择最多,就预测这个样本为该类。随机森林的训练过程总结如下:

1)给定训练集S,测试集T,特征维数F。确定参数:决策树的数量t,每棵树的深度d,每个节点使用到的特征数量f。终止条件:节点上最少样本数s,节点上最少的信息增益m。

对于第1-t棵树,i=1-t:

2)从S中有放回的抽取大小和测试集一样的训练集S(i),作为根节点的样本,从根节点开始训练。

3)如果当前节点上达到终止条件,则设置当前节点为叶子节点；如果是分类问题,该叶子节点的预测输出为当前节点样本集合中数量最多的那一类c(j),概率m为c(j)占当前样本集的比例；如果是回归问题,预测输出为当前节点样本集各个样本值的平均值。然后继续训练其他节点。如果当前节点没有达到终止条件,则从F维特征中无放回的随机选取f维特征。利用这f维特征,寻找分类效果最好的一维特征k及其阈值th,当前节点上样本第k维特征小于th的样本被划分到左节点,其余的被划分到右节点。继续训练其他节点。

4)重复2)、3),直到所有节点都训练过了或者被标记为叶子节点。

5)重复2)、3)、4),直到所有CART都被训练过[6-8]。

此处运用R软件对数据通过随机森林的方法进行处理。

1.2.1 确定决策树数量

首先寻找最佳参数ntree,即指定随机森林所包含的最佳决策树数目。通过R软件编程输出模型误差与决策树数量关系图如图2,易见当决策树数量大于等于300时,模型误差趋于稳定。因此选择300作为最佳决策树数量[9]。

图2 模型误差与决策树数量关系图

1.2.2 变量选择

为评价输入变量的重要性,可用importance成分绘制对各输入变量添加辛烷值后对整体预测精度平均影响的柱状图,如图3。

图3 输入变量重要性测度指标柱形图

由柱状图可知,模型中较为重要的有13个变量(由于数据量较大,横坐标的变量名称显示不完整),这里给出通过自查得出的结果,这13个变量分别为S-ZORB.LC_5001.PV、S-ZORB.TE_5202.PV、S-ZORB.FC_5202.PV、S-ZORB.FT_9202.PV、S-ZORB.TE_1105.PV、S-ZORB.PT_6002.PV、S-ZORB.FT_9101.TOTAL、S-ZORB.FT_3201.DACA、S-ZORB.DT_2001.DACA、S-ZORB.PDT_2001.DACA、S-ZORB.TE_7506.DACA、S-ZORB.TE_2104.DACA.PV、S-ZORB.PC_1001A.PV。

为更全面的评价各输入变量的重要性,可采用varImpPlot函数得到变量对预测错误率的影响排名及变量对GINI系数下降率的影响排名。变量对预测错误率的影响表示随机去掉一个特征,模型准确度下降的百分比,越高表明特征越重要；变量对GINI系数下降率的影响表示使用某一个特征进行分裂时,GINI系数下降的平均幅度,越高表明该特征的分裂质量越好,即该特征越重要。具体排名如图4、图5[10]。

图4 变量对预测错误率的影响

从对变量对预测错误率的影响的角度看,S-ZORB.PC_1001A.PV、S.ZOBB.PDT_3502.DACA、S-ZORB.DT_2001.DACA、S-ZORB.TE_1107.DACA、S-ZORB.TE_7506.DACA、S-ZORB.TE_5202.PV、 S-ZORB.TE_1001A.PV、 S-ZORB.FT_9302.PV、S-ZORB.AT.0009.DACA.PV、 S-ZORB.TE_6008.DACA等较为重要。

图5 变量对GINI系数下降率的影响

从变量对GINI系数下降率影响的角度看,辛烷值RON、 S-ZORB.TE_1001A.PV、S-ZORB.DT_2001.DACA、S-ZORB.TE_7506.DACA、S-ZORB.TE_5002.DACA、S-ZORB.TE_1201.PV、S-ZORB.LC_5101.PV、S.ZOBB.PDT_3502.DACA、性质辛烷值RON、S.ZOBB.PDP_35021003.DACA等变量对辛烷值损失的影响较大。

综合考虑三种角度提取的主要变量,选择S-ZORB.LC_5001.PV、S-ZORB.TE_5202.PV、S-ZORB.FC_5202.PV、S-ZORB.FT_9202.PV、S-ZORB.TE_1105.PV、S-ZORB.PT_6002.PV、S-ZORB.FT_9101.TOTAL、S-ZORB.FT_3201.DACA、S-ZORB.DT_2001.DACA、S-ZORB.PDT_2001.DACA、S-ZORB.TE_7506.DACA、S-ZORB.TE_2104.DACA.PV、S-ZORB.PC_1001A.PV将这13个较为重要的变量和原料的辛烷值共14个变量作为模型的主要变量。将此次降维得到的结果命名为结果2。

对比两种降维方法所得结果的拟合优度R2,结果2的R2较大,即随机森林的降维效果较好。

2 建立预测模型

沿用随机森林筛选出的主要建模变量,利用R语言编程分析降维后的变量与RON损失的线性关系,建立RON损失预测模型,并预测最后25个时间点的RON损失值。最后,通过预测结果与实际值的对比验证RON损失预测模型的可靠性[11]。

随机森林回归模型的确立主要分为两个步骤,首先是决策树的构建,其次是森林的形成。随机森林回归是由很多回归决策树模型{h(x,θk),k=1}组成的组合分类模型,且参数θk是独立分布的随机向量,在给定自变量X下,每个决策树回归都会有一个预测结果。它的基本思想与流程如图6。

图6 随机森林基本思想

其中，X:初始样本,Xi*:重抽样样本。

利用随机森林的预测过程如下:

对于第S棵树,i=1-t:

1)从当前树的根节点开始,根据当前节点的阈值th,判断是进入左节点

2)重复执行1)直到所有树都输出了预测值。如果是分类问题,则输出为所有树中预测概率总和最大的那一个类,即对每个c(j)的p进行累计；如果是回归问题,则输出为所有树的输出的平均值。

针对本文的研究对象,将前300个时间位点的数据作为训练数据,第301～325时间位点的数据作为检测数据即进行验证,因此先将降维后的主要建模变量利用R软件进行线性回归,输出结果如表4。

表4 随机森林回归结果

将辛烷值损失设为y,根据表中数据可得回归方程如下:

y=-8.928 0+0.006x2+0.008 2x30+

0.021 5x33+0.001 5x34+0.000 2x49-

0.000 3x68-0.425 8x78-0.000 3x191+0.001 9x246-0.006x249+0.019 1x338-

0.004 6x367,

(2)

根据上述回归方程通过R编程预测样本点301～325的RON损失值,然后对比样本观测值来验证预测结果的准确性,结果如表5。

表5 随机森林预测结果

再根据表中数据通过Excel进行作图,如图7。

图7 预测值与真实值的对比

从表5和图7可以看出,预测值与真实值的差别不大,因此可以认定本文所得RON损失预测模型是可靠的。

3 总 结

本文研究了一般石化企业的催化裂化汽油精制脱硫装置的模型构建。首先基于处理后的数据综合运用改进的因子分析法和随机森林法两种方法通过SPSS、R软件分别对变量进行降维处理并对比降维效果。其次,通过R语言编程分析降维后的变量与RON损失的线性关系,建立RON损失预测模型,并预测最后25个样本点的RON损失值。最后,通过预测结果与实际值的对比验证了RON损失预测模型的可靠性。

该问题的研究具有重要的理论意义和实际应用价值,后续还可进一步寻求其他模型检验以期达到更好的效果。