单螺杆压缩机转子异步压缩循环的动力学分析
2021-02-01彭程宇张曌谢佳吴伟烽冯全科
彭程宇,张曌,谢佳,吴伟烽,冯全科
(西安交通大学能源与动力工程学院,710049,西安)

符号表
盘型蜗轮-蜗杆机构作为气体压缩机是20世纪60年代发明的,半个世纪以来,世界上有十多个国家都在开发应用这种由两只盘型蜗轮(星轮)和一根蜗杆(螺杆)构成的压缩机,即单螺杆压缩机[1-4]。一直以来,单螺杆压缩机均采用单直线或者近似单直线结构的啮合副型线,但该型线容易磨损,使得其多在低压力和小型压缩机领域中发展,且发展缓慢[2-5]。进入21世纪以来,中国学者提出并开发了纯曲面啮合型线,解决了单螺杆压缩机啮合副,特别是星轮齿面的磨损问题,使得单螺杆压缩机在高压和大型化方向发展的前景倍现广阔[6-12]。
目前,市场上绝大部分的单螺杆压缩机是CP型(即螺杆为圆柱形、星轮为平面状),如图1所示,其螺杆齿槽数与星轮齿数之比为6∶11。通常认为采用这种齿数比的单螺杆压缩机,螺杆两侧的齿槽能够同步地进行吸气、压缩和排气过程,从而使螺杆转子受力均衡,具有良好的力学平衡性,能有效提高螺杆轴承寿命[13-16]。但是,近年来随着单螺杆压缩机往高压力和大排量方向发展,逐渐出现了振动大和噪声高等问题。研究表明,同步吸气、压缩、排气引起波动的阻力矩叠加是造成机器振动大和噪声高的主要原因。因此,本文提出在大排量、大压比及高压力领域中,采用螺杆转子奇数齿槽设计,利用奇数齿槽螺杆转子配合星轮片实现螺杆两侧工作腔异步工作,使得螺杆两侧压缩工质产生的阻力矩移步错峰,以有效减小气体压缩过程的阻力矩波动,降低压缩机的振动和噪声。
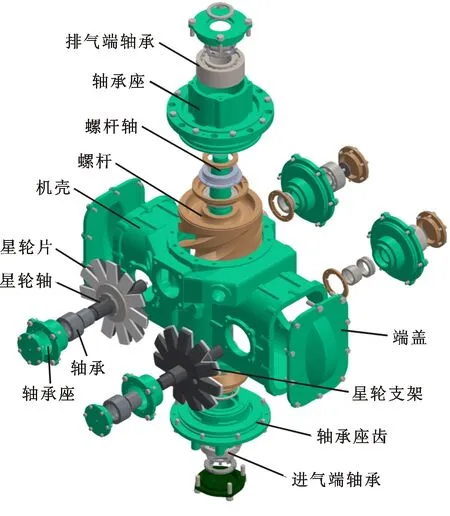
图1 单螺杆压缩机基本结构示意
在传统的同步压缩单螺杆压缩机中,认为螺杆转子受力平衡,对于单螺杆转子力学性能的研究和分析较少[17-19],但在异步压缩单螺杆压缩机中,其力学特征发生改变,因此有必要对异步压缩单螺杆压缩机螺杆转子的受力特征进行研究。本文基于单螺杆压缩机的工作特性,详细分析了异步压缩单螺杆压缩机在工作过程中螺杆转子的受力状况,建立了螺杆转子动力学模型,对异步压缩循环过程中螺杆转子的动力学规律进行探究,研究其动态变化以及对机组性能和长期稳定性的影响,从而为异步压缩单螺杆压缩机新产品的设计与开发提供理论支持。
1 螺杆转子受力分析
单螺杆压缩机螺杆转子工作时各工作腔的容积不同,压力也不同。压力不同会导致螺杆转子受到不平衡的气体力,是螺杆转子受力的主要原因。研究螺杆转子动力学特性,首先应该对螺杆转子上所受的力与力矩进行详细地分析,列出与其对应的力及力矩平衡方程。
如图2所示,螺杆转子受到由工质压力产生的气体力Fgr,i,该气体力垂直作用在螺槽表面,且气体力与作用面积在轴向矢量积为0。因此,该气体力仅为螺杆转子的径向力,为方便计算,将其平移到螺杆转子中心轴zr上,同时附加一个气体力矩Mgr,i。其次,螺杆转子与星轮片啮合,带动星轮轴系转动,啮合副间存在作用力Fmr,i,该作用力由齿面法向力Fnr,i和齿面摩擦力Ffr,i组成,其中齿面法向力Fnr,i可以分解成切向力Ftr,i、径向力Frr,i和轴向力Fzr,i。星轮齿与螺槽之间的摩擦力Ffr,i=μFnr,i,在实际工作过程中,星轮齿与螺槽间存在润滑介质,μ值较小,故计算中一般忽略齿面间的摩擦力。
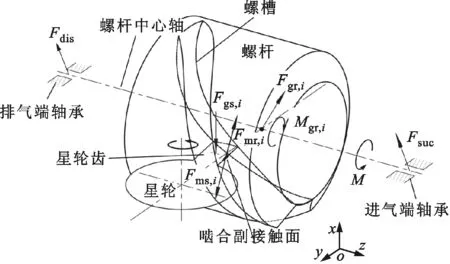
图2 螺杆转子所受力和力矩示意图
螺杆转子和螺杆轴紧固在一起,电动机的驱动力矩M通过螺杆轴传递到螺杆转子,螺杆轴由进气端和排气端的轴承支撑,作用在螺杆转子的径向力和轴向力由螺杆轴承的支反力平衡。
螺杆轴转速均匀,则螺杆转子处于平衡状态,螺杆转子的力和力矩可列平衡方程如下。
螺杆转子受力方程
∑(Fgr,i+Frr,i)=Fr-suc+Fr-dis
(1)
∑Fzr,i=Fz-suc+Fz-dis
(2)
螺杆转子力矩方程
∑(Mgr,i+Mtr,i)=M
(3)
图3为同步压缩与异步压缩过程示意图。从图中可以发现,在同步压缩过程中两侧星轮片同时啮入螺槽,而异步压缩过程中的星轮1和星轮2啮入螺槽时存在相位差。同步压缩过程中,螺杆转子两侧齿槽对称工作,螺杆转子所受气体力平衡,而在异步压缩过程中,由于螺杆转子两侧齿槽工作过程存在相位差,螺杆转子所受气体力不平衡,需要进一步研究。

(a)同步压缩过程
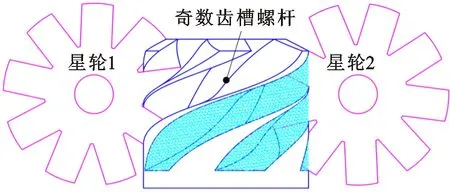
(b)异步压缩过程图3 同步压缩与异步压缩过程示意图
2 啮合副间作用力的数学模型
螺杆转子通过螺槽与星轮片的接触推动星轮轴系转动,理论上螺槽与星轮片之间不存在间隙,因此在任意一个瞬间都同时存在有多个啮合点接触,且各啮合点处均存在作用力,是一个典型的非静定受力关系。本文根据机械传动原理,通过计算星轮轴系的阻力矩变化来间接确定其驱动力的大小,从而求解螺杆转子齿槽与星轮齿之间的作用力,假设如下:
(1)啮合副型线加工无误差,啮合副之间可完全正确啮合;
(2)假设螺杆转子和星轮均为刚体,不会出现弹性形变;
(3)螺杆转子与星轮在工作过程中均为匀速转动,处于平衡状态;
(4)忽略啮合副之间摩擦力以及啮合冲击的影响。
螺杆转子与星轮片在接触位置产生的作用力由齿面法向力Fnr,i和齿面摩擦力Ffr,i组成。如图4所示,将作用在螺杆转子上的齿面法向力正交分解成切向力Ftr,i、径向力Frr,i和轴向力Fzr,i。
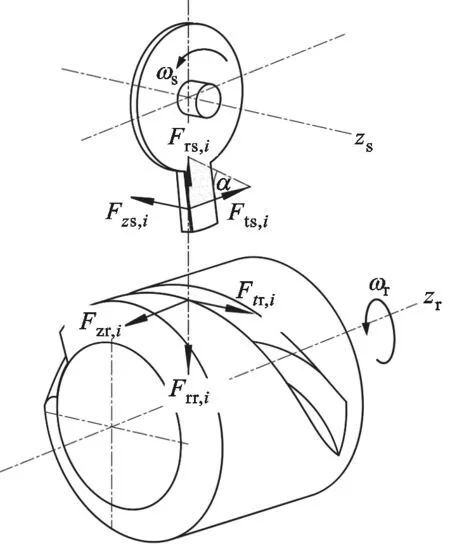
图4 啮合面法向力分解示意图
作用在星轮齿上的齿面法向力与作用在螺杆转子上的齿面法向力大小相等方向相反,也将其正交分解成切向力Fts,i、径向力Frs,i和轴向力Fzs,i,且有如下关系
(4)
Mts,i=PηMtr,i
(5)
在工作过程中,星轮为匀速运动,认为星轮轴系处于受力平衡状态,如图5所示。
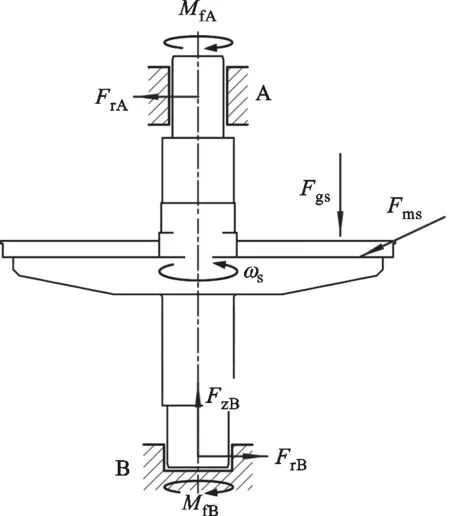
图5 星轮轴系受力示意图
星轮轴系力和力矩平衡方程如下[20]
(6)
MfA=FfARA=FrAμrARA
(7)
(8)
以轴承A的中心位置为矩心,则
FrBLAB-FzsDjs/2-∑Fgs,iRc-∑Frs,iLOA=0
(9)
联立式(4)~(9)进行求解,便可得到螺杆转子工作过程中啮合副之间的作用力。
3 螺杆转子气体力数学模型
单螺杆压缩机通过电机驱动螺杆轴系,带动螺杆转子与星轮片完成啮合,实现工作腔的容积变化。星轮齿在螺杆转子的带动下啮入螺槽,将每个螺槽分隔成上下两个空间实现吸气、压缩和排气过程,工作腔容积随星轮转角的变化而变化,从而导致其内部工质压力也发生变化,螺杆转子所受的气体力则是由工作腔内工质压力产生的。
单螺杆压缩机工作过程中,由于传热、泄漏、喷液以及气体偏离理想气体特性,实际气体压力的变化非常复杂[16,21]。本文主要研究气体力的变化规律,故对工作过程中的气体力做如下假设:
(1)不考虑吸、排气阻力损失,吸气压力为大气压;
(2)封闭容积内气体的压缩过程为绝热过程,绝热指数κ=1.4;
(3)封闭容积内气体均匀分布,其压力、温度各处相等。
这些假设使得理论分析相对变得简单,但研究结果却能客观地反映实际情况。
单螺杆压缩机工作过程如图6所示。压缩机的工作腔是由螺杆螺槽内表面、啮入螺槽的星轮齿顶面以及机壳内表面构成的封闭容积,容积内工质具有一定的压力,从而产生气体力。该气体力满足如下方程
pdS=0
(10)

图6 单螺杆压缩机工作过程示意图
同时
(11)
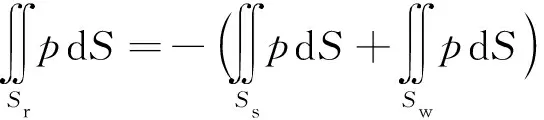
(12)
因此,单螺杆压缩机工作过程中螺杆转子受到的工作腔气体力等于机壳内表面和啮入螺槽星轮齿顶表面受到的气体力之和。
3.1 机壳内表面气体力数学模型
机壳内表面沿圆周方向展开图如图7所示,在组成封闭工作腔的机壳内腔面上任取一平行于螺杆中心线的微元面积dS,微元面积的轴向长度为l,宽度为dδ,星轮齿上表面转至该微元对应的星轮转角为α。
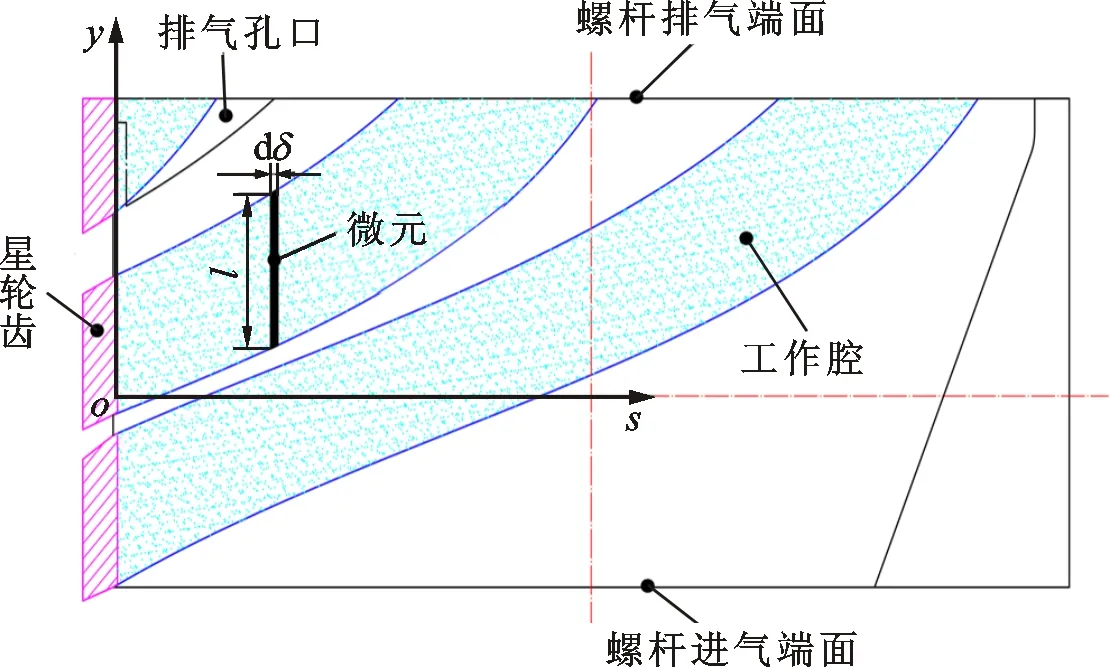
图7 机壳内表面沿圆周方向展开示意图
微元的轴向长度与微元对应的星轮转角的关系为
(13)
故微元面积
dS=l(α)dδ=l(α)PRrdα
(14)
当星轮转角为α时,该微元承受的气体力为
dF=p(α)dS
(15)
其中p(α)为工作腔气体压力,其在一个啮合周期内随星轮转角的变化关系如下[12]
(16)
微元在机壳内表面的位置如图8所示,其长度方向与螺杆轴线平行,微元上气体力与水平方向的夹角为
(17)

图8 微元空间位置示意图
将机壳内表面微元上的气体力进行正交分解,然后积分求和,故工作腔内的气体作用在机壳内表面的气体力为
(18)
3.2 星轮齿顶面气体力数学模型
星轮在螺杆转子的带动下啮入、啮出螺槽,造成工作腔的星轮齿面积随星轮转角的变化而变化。
如图9所示,在组成封闭工作腔的星轮齿面上平行于星轮中心轴线位置处,任取一长为dτ、宽度为dη的微元,其面积为dS。
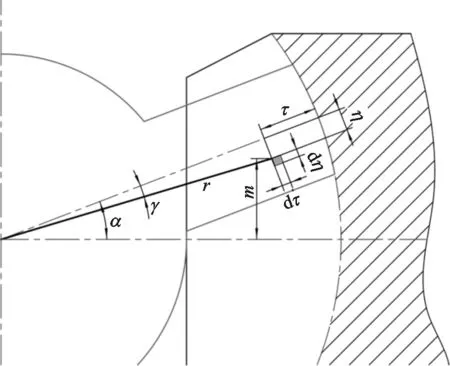
图9 星轮齿微元示意图
当星轮转角为α时,作用于微元面积的气体力为
dFgs(α)=p(α)dτdη
(19)
对该微元面积上所受的气体力在齿宽和齿长范围内进行二重积分,得到该星轮齿上受到的气体力,因此该部分作用力可表示为
(20)
3.3 螺杆转子轴承支反力数学模型
气体力作用在螺杆转子的螺槽表面,随着螺杆转子的转动,螺槽的空间位置发生变化,其等效集中作用点的空间位置也随之改变。气体力可以通过机壳内表面和星轮齿顶面气体力模型求解,但由于其理想集中点的空间位置不断改变,无法得知进、排气端轴承支反力具体变化特性,因此需要对机壳内表面和星轮齿顶面气体力模型进行改进,以便准确得到螺杆转子轴承的支反力。
如图7所示,微元受到气体力的集中作用点可近似认为在其线性几何中心处,微元面积在螺杆轴线y方向上的两个边界分别为封闭螺槽的前后侧螺旋线。由文献[14]可知,封闭螺槽后侧螺旋线在y方向方程为
(21)
因此,微元面积作用点在y方向坐标位置可表示为
(22)
将机壳内表面气体力等效到支撑轴承,以吸气端轴承为例
(23)
如图9所示,星轮齿上表面微元受到的气体力集中作用点距螺杆与星轮中心连线距离为
(24)
将星轮齿上表面气体力等效到支撑轴承,同样以吸气端轴承为例

(25)
4 模型求解和计算结果
选择一定的结构参数,对以上模型进行求解。以某一高压压缩机为例,压缩工质为空气,结构参数与操作参数如表1所示。

表1 模型中压缩机结构参数与操作参数
图10和图11是单螺杆压缩机中螺杆转子在单侧压缩腔作用时齿面法向力和气体力随星轮转角的变化,星轮转角以两侧星轮中心连线位置为起始位置,转角方向与星轮转动方向一致时取正,反之取负。从图中可以看出,单侧压缩腔作用时,螺杆转子所受齿面法向力和气体力是以转过两星轮齿夹角所需时间的1/2为变化周期,其中齿面法向力在轴向分力最大,但它在数量级上却远小于气体力的数量级,因此螺杆转子支撑轴承设计与选取主要依据径向气体力大小。
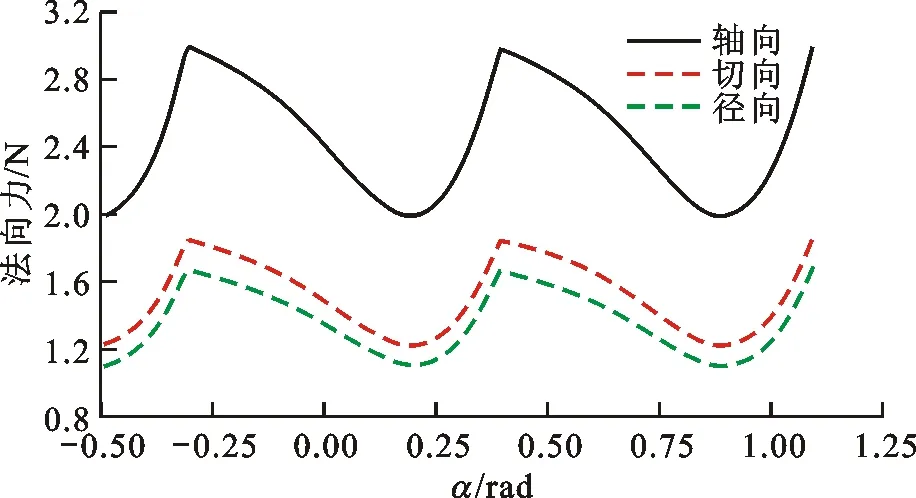
图10 单侧压缩腔作用时螺杆转子所受齿面法向力随星轮转角的变化
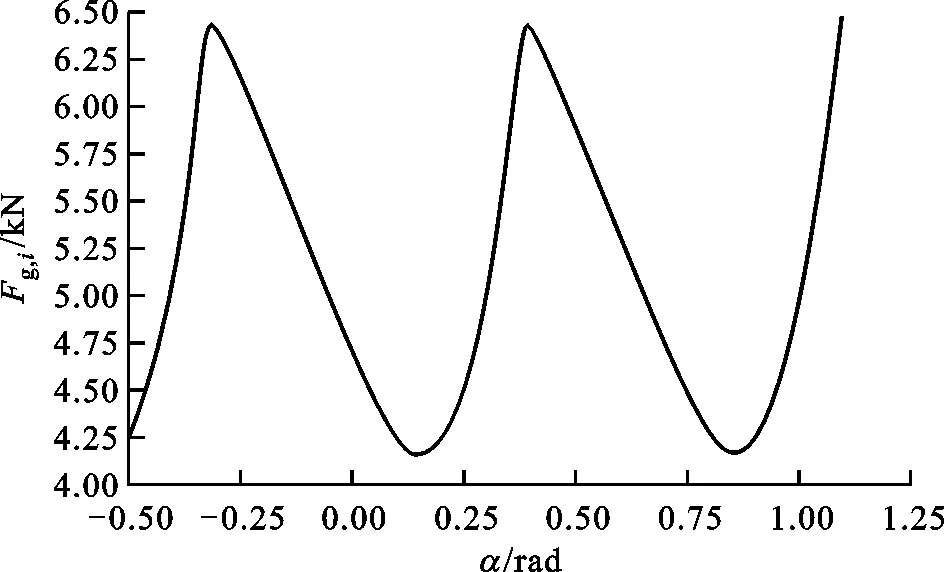
图11 单侧压缩腔作用时螺杆转子所受径向气体力随星轮转角的变化
在同步压缩过程中,螺杆转子两侧由于对称压缩工质,气体力相互平衡,而齿面法向力无法平衡,是单侧压缩腔作用时螺杆转子所受齿面法向力的2倍,因而螺杆转子具有一定量的轴向载荷,该载荷大小与星轮轴系的质量以及轴承的润滑性能有密切关系。因此,传统认为螺杆转子在同步压缩循环过程中受力完全平衡是有一定局限性的。
在异步压缩的单螺杆压缩机中,由于螺杆转子两侧工作过程相位差的存在,使得其啮合副之间作用力比相同尺寸同步压缩的单螺杆压缩机小一些。异步压缩过程中两侧压缩腔的气体力会相互抵消,气体力比单侧压缩腔的气体力小很多,本算例中径向气体力最大值为2 kN左右,远小于其单个支撑轴承18 N的额定径向载荷,如图12所示。

图12 异步压缩循环中径向气体力随星轮转角的变化
图13为异步压缩循环中螺杆转子径向气体力在一个变化周期内的空间矢量分布图。从图中可以看出,该作用力不仅大小不断变化,方向也沿着螺杆转子的径向不断旋转,最大值位于y轴正方向逆时针30°的直线上,此方向也是两侧支撑螺杆转子的轴承支反力最大的方向(具体坐标轴参考图2)。

图13 螺杆转子所受气体力矢量分布图
根据支撑轴承受到螺杆转子气体力的数学模型计算分析可以得到图14。由图可知,螺杆转子所受气体力等效集中位置随着星轮齿转角的变化在螺杆中心面与排气端面之间呈周期性变化,且在星轮齿转角为-0.3、0、0.3、0.6、0.9 rad时发生突变。经分析不难发现,上述角度均为异步压缩过程工作腔开始排气的角度,接通排气孔口后,由于两侧孔口位置对称,排气压力对螺杆的气体力互相抵消,此刻气体力的作用位置发生突变,向中心面靠近。由于气体力等效集中点位置的变化会引起螺杆轴的弯矩发生周期性变化,因此在设计时需要考虑由该气体力引起的螺杆轴的弯矩。
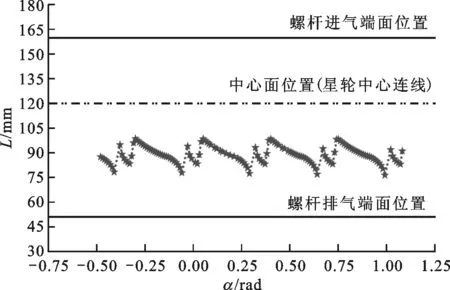
图14 气体力等效集中位置随星轮转角的变化
5 结 论
本文针对传统大排量、大压差单螺杆压缩机工作过程中阻力矩波动大、噪音高等问题,创新性地提出螺杆转子奇数齿槽结构,并基于力学基本原理及单螺杆压缩机工作特性,建立了异步压缩单螺杆压缩机螺杆转子受力计算模型,对螺杆转子所受啮合副间作用力及工作腔内气体力进行了理论分析计算,研究了异步压缩循环中螺杆转子的受力特征,得到如下结论。
(1)通过同步压缩与异步压缩单螺杆压缩机螺杆转子受力状况对比分析,指出同步压缩单螺杆压缩机的螺杆转子径向气体力平衡,啮合副之间作用力不平衡,而异步压缩单螺杆压缩机螺杆转子径向气体力与啮合副之间作用力均不平衡。
(2)基于啮合原理以及单螺杆压缩机中星轮片和螺杆转子受力特征,建立了啮合副之间作用力数学模型和螺杆转子气体力数学模型,阐释了作用在机壳、星轮片以及螺杆转子上的气体力之间的相互关系。
(3)以一台两立方高压单螺杆压缩机为例,对螺杆转子受力情况进行分析,结果表明,传统认为同步压缩单螺杆压缩机螺杆转子受力完全平衡这一观点有一定的局限性,在同步压缩单螺杆压缩机的设计过程,不能忽略由啮合副之间作用力产生的轴向力。同时,异步单螺杆压缩机螺杆转子所受气体力不仅大小不断变化,方向也沿着螺杆转子的径向不断旋转,其在螺杆转子上的等效作用位置在螺杆排气端面与中心面之间周期性变化,在工作腔接通排气孔口时会发生突变。该气体力以转过两星轮齿夹角所需时间的1/2为变化周期,远小于两侧支撑轴承的额定载荷,且最大气体力方向位于水平方向逆螺杆旋转方向旋转30°过螺杆转子轴心的直线上。这些力学变化特征,可为异步压缩的单螺杆压缩机设计与轴承选用提供可靠的指导意见。
(4)本文的模型建立在螺杆转子与星轮片的啮合副无间隙、压缩工质无泄漏的情况下,在实际机器中,这些间隙总是存在液膜的作用力,因此计算啮合副之间作用力时,需要进一步考虑液膜造成的影响,以建立更合理的模型对其进行研究。同时,在异步压缩单螺杆压缩机中径向气体力对螺杆转子的作用会引起螺杆轴的弯矩,导致螺杆轴的偏心、形变,甚至螺杆轴系共振,这些问题也是将来的研究重点。
