对数变换主成分分析的图像识别
2021-02-01宋昱孙文赟陈昌盛
宋昱,孙文赟,陈昌盛
(1.深圳大学电子与信息工程学院,518060,广东深圳;2.深圳大学深圳市媒体信息内容安全重点实验室,518060,广东深圳;3.深圳大学广东省智能信号处理重点实验室,518060,广东深圳)
主成分分析(PCA)[1]是一种线性变换算法,在图像处理和机器学习中有很多重要的应用。PCA将高维数据投影至低维空间,可以有效地表示高维数据。然而,PCA也有一些缺点。因为PCA采用l2范数的平方衡量原样本与重构样本的误差,所以当数据中有些样本明显远离其他样本,即数据中含有异常样本时,这些异常样本会对PCA的目标函数造成显著的影响[2-5],从而导致标准PCA不能很好地处理含有异常样本的数据。
为了减小异常样本带来的负面效果,研究者提出了很多鲁棒PCA算法。文献[6]和文献[7]通过对样本进行最大似然估计,得到了基于l1范数的PCA算法。文献[6]采用启发式的估计算法检测异常样本,文献[7]采用凸优化算法检测异常样本。文献[8]采用非凸M估计算子作为目标函数,学习得到彩色图像的表示。尽管这些算法具有对异常样本的鲁棒性,但是有一个共同的缺点,即不具有旋转不变性,而旋转不变性是学习算法应具有的一个重要性质[9]。为了保留标准PCA算法的旋转不变性,研究者提出了一些鲁棒的旋转不变PCA算法[3-4,10-13]。文献[10]提出了PCA-L1,采用贪婪算法最大化投影后样本的l1范数。文献[11]提出了一种非贪婪算法,以此求解PCA-L1的目标函数,可以同时求解所有的投影方向。为了扩展PCA-L1算法,文献[12]提出了PCA-Lp算法,该算法最大化投影后样本的lp范数。PCA-L1或者PCA-Lp并没有最小化重构误差,而是最大化投影后样本的l1或者lp范数,其目标函数与标准PCA的目标函数有本质不同。文献[3]和文献[4]提出了R1-PCA,其目标函数中使用了2种范数,在样本空间维度上使用了l2范数,在样本间使用了l1范数。文献[13]提出了Φ-PCA,其目标函数是一个二阶可导的凸函数,可以采用牛顿迭代法求解。然而,R1-PCA和Φ-PCA假设数据是均值的,该假设在实际中有一定的限制[14]。为了估计样本均值,文献[15]提出了基于最大相关熵的PCA。为了进一步扩展R1-PCA,文献[16]提出了基于l2,p范数的PCA。该算法采用l2,p范数衡量原样本与重构样本的误差,当p=1时,该算法与R1-PCA算法等价。
尽管研究者已经提出了众多的鲁棒PCA算法,但是这些算法在处理含有异常样本的数据时依然有一些不足。以基于l2,p范数的PCA算法为例,不能在理论上保证该算法的目标函数值小于标准PCA算法的,从而其处理异常样本的性能不能得到保证。为了改进现有的鲁棒PCA算法,本文提出了一种基于对数变换的鲁棒PCA算法,可以在理论上证明所提算法的目标函数值小于标准PCA算法的,从而提高现有鲁棒PCA算法处理含有异常样本数据的能力。所提算法保留了标准PCA算法的性质,即具有旋转不变性,且投影矩阵与数据协方差矩阵相关。实际数据集上的实验结果证明了所提算法的有效性。
1 标准PCA算法和鲁棒PCA算法
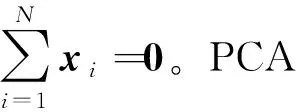
(1)
式中Ik是k×k的单位矩阵。通过代数运算,可以得出目标函数式(1)等价于
(2)
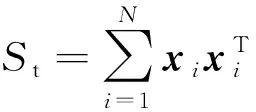
从目标函数式(1)可以看出,PCA在平方的意义上最小化重构误差,使得目标函数对于异常样本非常敏感[3-5]。异常样本重构误差的平方非常大,对于目标函数有显著影响,会影响得到的投影矩阵。为此,研究者提出了很多鲁棒PCA算法,例如基于l1范数的PCA算法[11-12],该算法的目标函数为
(3)
基于l1范数的PCA算法通过求解目标函数式(3)得到投影矩阵。目标函数式(3)的解与协方差矩阵的关系并不清楚,而且因为‖xi-WWTxi‖1+‖WTxi‖1≠‖xi‖1,目标函数式(3)并没有最小化重构误差。PCA算法的目标函数最小化了重构误差,这说明目标函数式(3)与PCA算法的目标函数有本质不同。目标函数式(3)的解不等价于
(4)
目标函数式(4)直接考虑了数据的重构误差,并且对异常样本具有一定的鲁棒性。然而,目标函数式(4)不容易求解,其求解算法的计算量很大[3],而且目标函数式(4)不具有旋转不变性。为了改进基于l1范数的PCA算法,文献[16]中提出了基于l2,p范数的PCA算法,其目标函数为
(5)
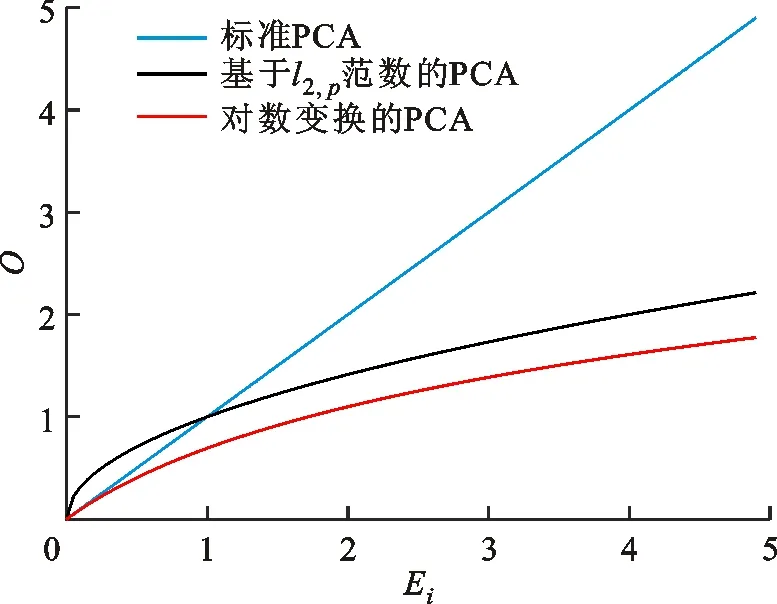
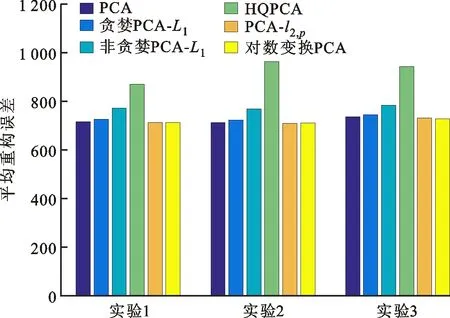
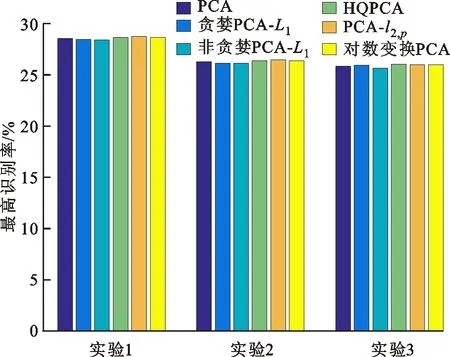
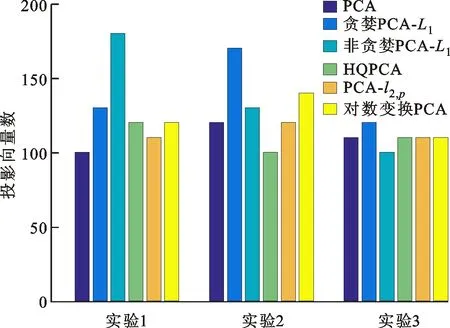
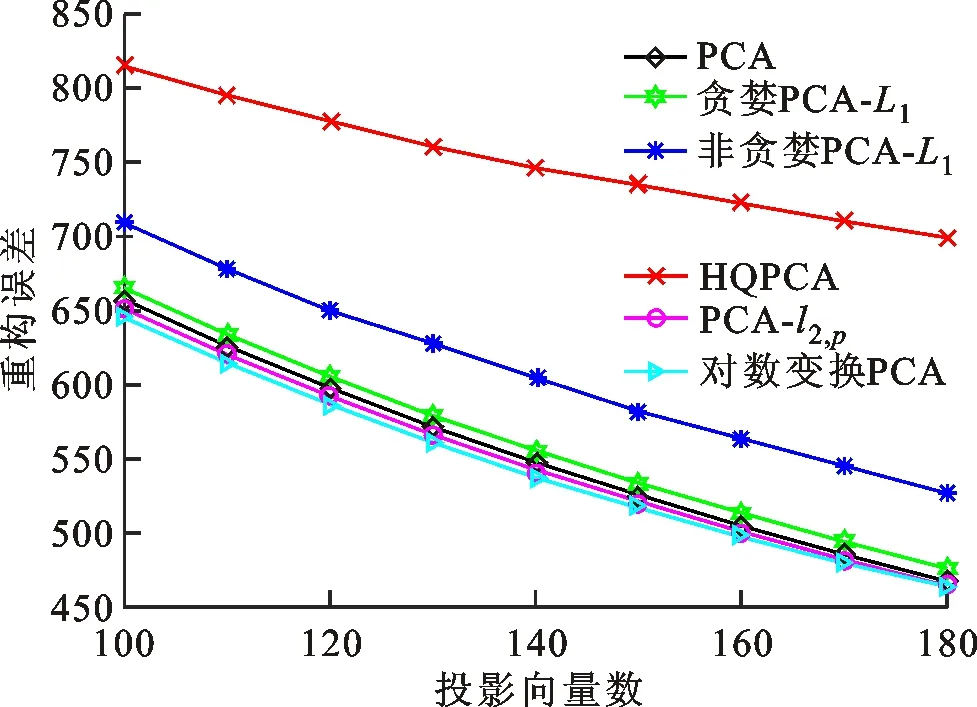
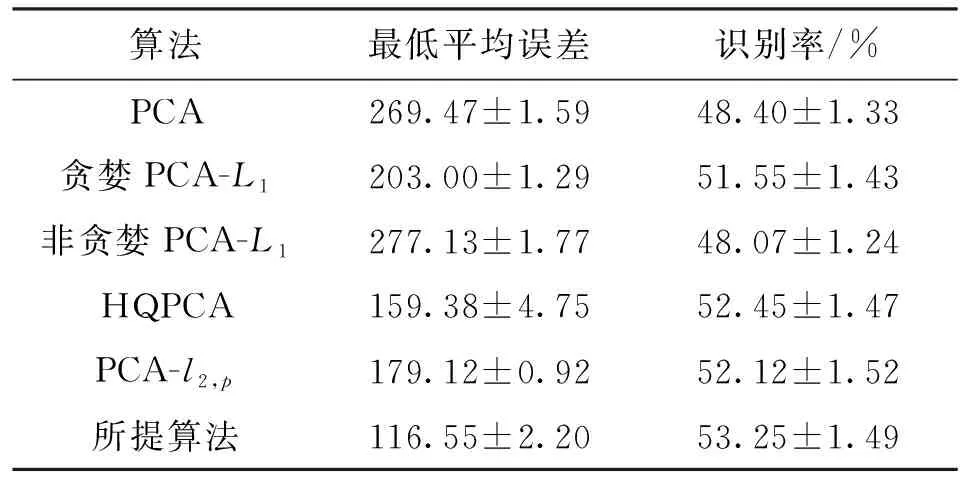
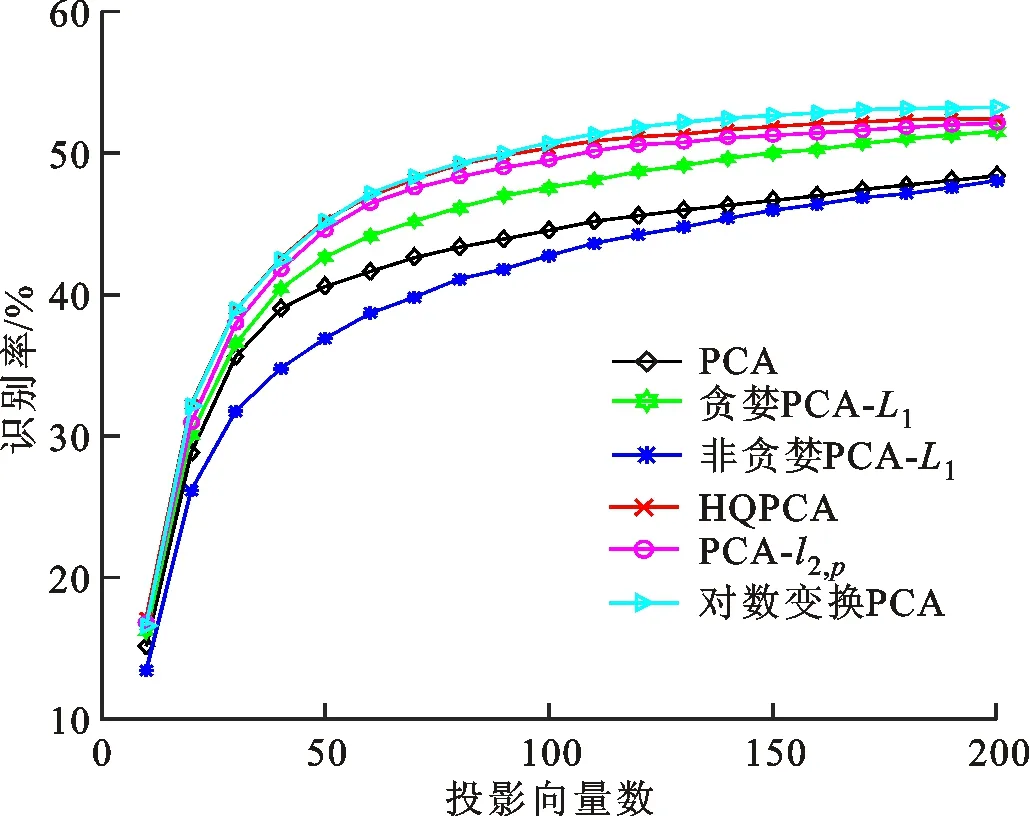
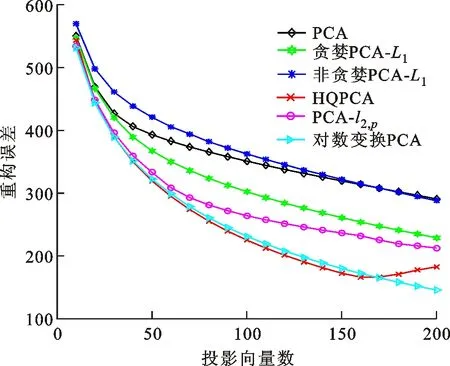
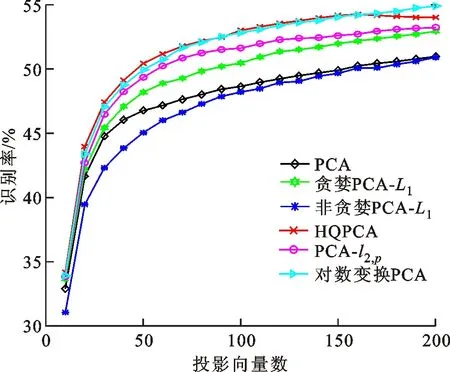
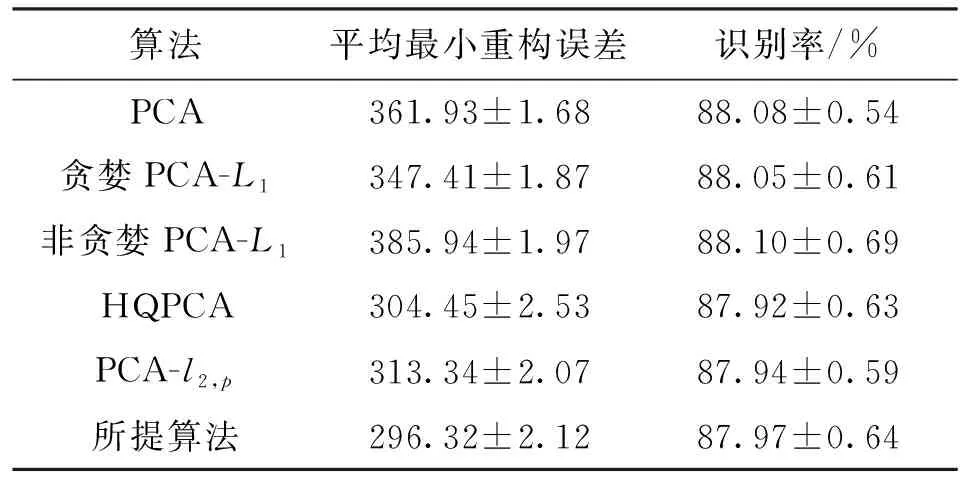
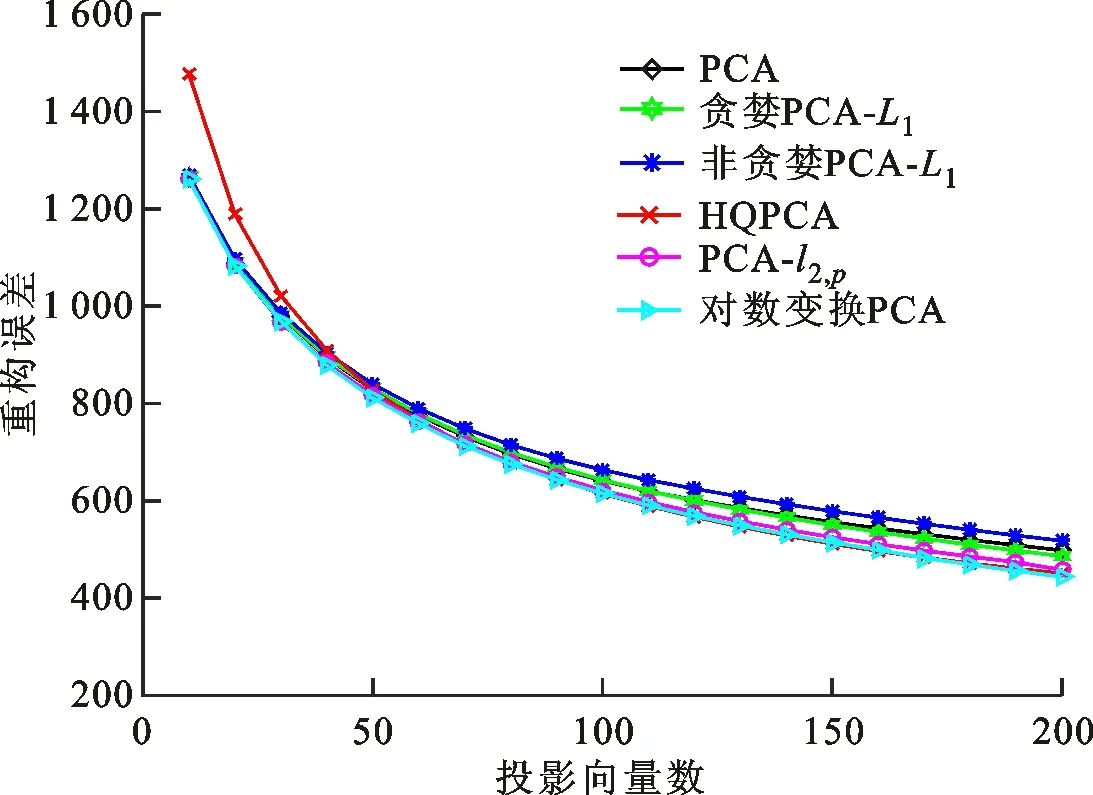
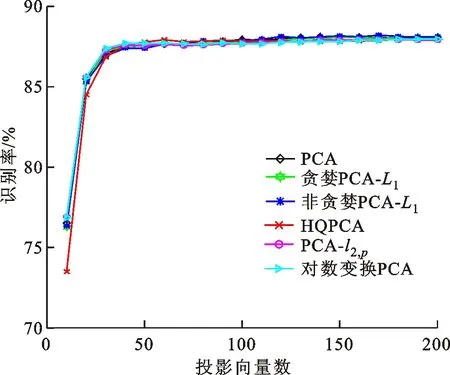
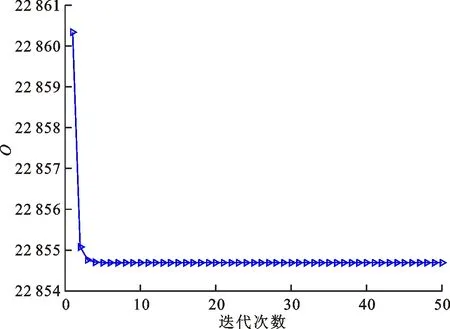
式中0 为了从理论上保证所提算法的目标函数值小于目标函数式(1)的,采用对数形式。当x≥0时,有 x≥ln(x+1) (6) (7) 进一步得到 (8) 这样就从理论上保证了重构误差的减小,而不等式(8)的右侧即为本文采用的目标函数,即 (9) 通过代数运算,可以得到 (10) (11) (12) 式中D是一个对角矩阵,其对角线上的元素是di。根据矩阵理论,目标函数式(12)中W*的列向量应是对应于矩阵XDXT最大的k个特征值的特征向量。求解出矩阵W后,再更新di。重复上述迭代过程直至收敛,收敛条件为 (13) 式中:Ot和Ot-1分别表示在第t次和第t+1次目标函数式(9)的取值;ε是一个小的常数,取为10-3。 求解目标函数式(9)的优化算法为对数变换的PCA,即算法1,伪代码如下。 输入:X=[x1,…,xN]∈Rd×N,k while 不收敛 do 1.计算对角矩阵D,其对角线上的元素为 2.计算加权协方差矩阵XDXT 4.t=t+1 end while 输出:Wt∈Rd×k 定理1在算法1的每一次迭代中,有 (14) 证明根据算法1,在第t+1次迭代时,有 (15) (16) (17) (18) (19) (20) 对数函数ln(·)是凹函数,满足式(20),即 (21) (22) 结合不等式(19),可以得到不等式(22)的右侧小于0,所以可得 (23) 定理2算法1近似收敛于目标函数式(9)的最优解处。 证明目标函数式(9)是约束优化问题。采用拉格朗日乘子法,将其转换为非约束优化问题。目标函数式(9)对应的拉格朗日函数为 tr(ΛT(WTW-I)) (24) 式中Λ是拉格朗日乘子。为了满足约束条件WTW=Ik,Λ应设为对角矩阵。根据KKT条件,在最优解处有dL=0。对式(24)取微分,可得 tr(WΛT(dW)T) (25) 为了使得dL=0,应满足 (26) 目标函数式(12)的最优解在算法1的第3步得到,所以算法1收敛时的解满足目标函数式(12)的KKT条件。目标函数式(12)的拉格朗日函数为 (27) 对L2取微分,并令其微分为0,可得 (28) 旋转不变性意味着投影结果,即高维数据的低维表示,在样本空间经过旋转后保持不变。 定理3算法1的解具有旋转不变性。 证明任意给定一个旋转矩阵Γ(ΓTΓ=I),投影矩阵W和样本xi的旋转变换表示为 (29) 因为ΓTΓ=I,从而可得 (30) 将式(29)和式(30)进行结合,算法1的目标函数可以表示为 (31) (32) 样本xi的低维表示在旋转变换下并不改变。证毕。 图1 重构误差与目标函数值的关系 与现有的PCA-L1算法相比,所提的基于对数变换的PCA算法最小化重构误差,与PCA算法的目标一致。与目标函数式(4)对应的算法相比,所提算法保留了PCA算法的旋转不变性。与基于l2,p范数的PCA算法相比,在理论上所提算法的目标函数值小于PCA算法的,避免了l2,p范数放大较小重构误差的缺点。所提算法具有良好的收敛性。 为了验证所提算法的有效性,在AR、Extended Yale B和CMU PIE共3个人脸数据集及MNIST共1个手写字符数据集上进行了实验,和标准PCA算法[1]、贪婪求解的基于l1范数的PCA算法[10](记为贪婪PCA-L1算法)、非贪婪求解的基于l1范数的PCA算法[11](记为非贪婪PCA-L1算法)、基于最大相关熵的PCA算法[15](记为HQPCA算法)以及基于l2,p范数的PCA算法[16](记为PCA-l2,p)进行了比较。设置PCA-l2,p算法的p=1。使用最近邻算法对降维后的数据进行分类,近邻数取为1。投影向量数k从10取到200。重构误差为 (33) AR数据集[17]包含126人的超过4 000幅彩色正面人脸图像,实验中转为灰度图像。实验选择其中119人(65名男性和54名女性)的3 094幅图像作为数据集。这些图像在2个时段拍摄(相隔2周)。每个时段包含13幅图像,6幅图像有眼镜或围巾遮挡,7幅图像有不同表情和光照。从每幅图像中选出人脸区域,并将图像大小调整为50×40像素[18]。图2是AR数据集中的某人图像,图像a~m来自第1个时段,图像n~z来自第2个时段。 abcdefghijklm 在AR数据集上,进行3组实验,实验1是眼镜遮挡实验,实验2是围巾遮挡实验,实验3是眼镜和围巾遮挡实验。在实验1中,选择每人10幅图像,即图像a~j作为训练样本,图像n~w作为测试样本,其中被眼镜遮挡的图像是异常样本。在实验2中,选择每人10幅图像,即图像a~g和k~m作为训练样本,图像n~t和x~z作为测试样本,其中被围巾遮挡的图像是异常样本。在实验3中,选择每人13幅图像,包括第1个时段的13幅图像a~m作为训练样本,其他图像作为测试样本,被眼镜或者围巾遮挡的图像是异常样本。 图3是AR数据集上的平均重构误差和最高识别率。从图3a可以看出:在实验1和2中,所提算法的重构误差与PCA-l2,p算法的接近,2种算法的重构误差小于其他4种算法的;在实验3中,所提算法的重构误差最小,优于其他算法的;在所有实验中,HQPCA算法的重构误差明显高于其他算法的。从图3b可以看出,所提算法和HQPCA算法以及PCA-l2,p算法的识别率接近,高于其他3种算法的。 (a)平均重构误差 (b)最高识别率图3 AR数据集上的平均重构误差和最高识别率 图4是AR数据集上的性能比较。从图4a可以看出,当投影向量数在100~180时,各算法取得最高的识别率,由此表明投影向量数在100~180变化时,对各算法有重要影响。从图4b中可以看出,当投影向量数在100~180时:所提算法取得了最小重构误差;PCA-l2,p算法取得了较小的重构误差;HQPCA算法的重构误差较大。对于AR数据集上的3类实验,在第1、2类实验中分别加入了被眼镜遮挡的样本和被围巾遮挡的样本作为异常样本,异常样本数量占的比例较小。实验1和实验2不能充分体现鲁棒PCA算法处理含有异常样本数据集的优越性。实验3中加入了被眼镜和围巾遮挡的样本作为异常样本,异常样本占比明显高于实验1和实验2的。实验3上的结果更能体现鲁棒PCA算法的优越性。综合可知,所提算法在实验3上取得了最小的重构误差,且取得了较高的识别率。 (a)取得最高识别率时对应的投影向量数 (b)实验3的重构误差图4 AR数据集上的性能比较 Extended Yale B数据集[19]包含了来自38人的2 144幅在不同光照下的图像。在该实验中,将人脸图像的大小调整为32×32像素[18]。从每个人的图像中随机选取14幅图像,然后随机选取图像的一部分,将这部分替换为含有椒盐噪声的图像块。该图像块只包含像素值为0和255的点,大小取为12×12像素。图5是Extended Yale B数据集中的部分正常图像和含噪图像。对于每一个人,随机选取25幅正常图像和7幅含噪图像作为训练样本,该人的其他图像作为测试样本。实验重复10次。 (a)正常图像 (b)含噪图像图5 Extended Yale B数据集中的部分图像 表1是Extended Yale B数据集上各算法的最低平均重构误差和对应的识别率,表中以“量值±标准差”的形式表示。 表1 Extended Yale B数据集上各算法的最低平均误差和对应的识别率 图6是Extended Yale B数据集上各算法的性能比较。从图6和表1中可以看出:所提算法在数据重构和分类上的性能明显优于其他5种算法的,性能仅次于所提算法的是HQPCA算法,再次是PCA-l2,p算法;HQPCA在投影向量数从190变为200时,重构误差下降,而其他5种算法依然保持上升;PCA算法性能不佳,这是因为数据集中含有异常样本,而异常样本对PCA算法的重构误差有较大影响;贪婪和非贪婪PCA-L1算法由于没有直接最小化重构误差,而是最大化投影后向量的l1范数,所以性能也不佳;所提算法优于PCA-l2,p算法,这是因为所提算法没有放大小的重构误差,对于大的重构误差也有更大的抑制,所以所提算法取得了最优的性能。在Extended Yale B数据集上实验结果与理论分析一致,且与AR数据集上的实验结果一致。 (a)重构误差和投影向量数的关系 (b)识别率和投影向量数的关系图6 Extended Yale B数据集上各算法的性能比较 CMU PIE数据集[20]包含了来自68人的2 856幅正面人脸图像。每人含有42幅在不同光照条件下拍摄的图像。在该实验中,将每幅图像的大小调整为32×32像素[18],并且加入了类似于在Extended Yale B数据集的实验中加入的噪声。从每人的图像中随机选择10幅图像加入噪声。图7是部分CMU PIE数据集上的人脸图像和含噪图像。随机选取每个人的21幅图像(16幅正常图像和5幅含噪图像)作为训练样本,其他图像作为测试样本。实验重复10次。 (a)正常图像 (b)含噪图像图7 CMU PIE数据集中的部分图像 表2是CMU PIE数据集上各算法的平均最小重构误差和对应的识别率。 表2 CMU PIE数据集上各算法的平均最小重构误差和对应的识别率 图8是CMU PIE数据集上各算法的性能比较。从表2和图8可以看出:所提算法取得了最优的性能,性能仅次于所提算法的是HQPCA算法;对于HQPCA算法,当投影向量数较小时,其性能与所提算法接近,随着投影向量数的增加,其性能达到最优后开始变差,而所提算法的性能随着投影向量数的增加一直增加,并且优于HQPCA算法的最优性能。在CMU PIE数据集上的实验结果与理论分析一致,并且与在AR数据集和Extended Yale B数据集上的实验结果一致。 (a)重构误差和投影向量数的关系 (b)识别率和投影向量数量的关系图8 CMU PIE数据集上各算法的性能比较 MNIST数据集[21]共包含了70 000幅手写数字图像,其中训练集有60 000幅图像,测试集有10 000幅图像。每幅图像的大小是28×28像素,手写数字位于图像中间。在本实验中,从测试集中选取5 000幅图像,每个字符(即0~9)包含500幅图像。从每个字符的图像中随机选取120幅图像,然后随机选取图像的一部分,将这部分替换为含有椒盐噪声的图像块,图像块的大小取为10×10像素。对于每一个字符,随机选取190幅正常图像和60幅含噪图像作为训练样本,该字符的其他图像为测试样本。实验重复10次。表3是MNIST数据集上各算法的平均最小重构误差和对应的识别率。 表3 MNIST数据集上各算法的平均最小重构误差和对应的识别率 图9是MNIST数据集上是各算法的性能比较。从表4和图9a可以看出:所提算法取得了最小的重构误差,HQPCA算法和PCA-l2,p算法也取得了较好的性能,它们的性能都优于其他3类算法的;当投影向量数较小时,HQPCA算法的重构误差略小于所提算法的,而当投影向量数量增大时,所提算法的性能逐渐优于HQPCA算法的。从图9b可以看出:各算法的识别率非常接近,最高的识别率(PCA)与最低的识别率(HQPCA)之间的差距为0.16%,基本可以忽略;当投影向量数较少时,所提算法取得了最高的识别率。综上可知,所提算法的特征提取性能优于其他对比算法的。 (a)重构误差和投影向量数的关系 (b)识别率和投影向量数的关系图9 MNIST数据集上各算法的性能比较 AR数据集上实验3的目标函数值与迭代次数的关系曲线如图10所示,投影向量数k=10。可以看出,所提算法的目标函数值迅速减小至收敛,大概在第5次迭代时即可达到收敛。图10的结果与2.3小节中对于算法收敛性的理论分析一致,所提算法可以得到目标函数的最优解。 图10 所提算法目标函数值与迭代次数的关系曲线 本文提出了一种鲁棒PCA算法——基于对数变换的PCA算法。从对数变换的性质出发,导出了所提算法使用的目标函数。所提算法的目标函数值和标准PCA算法的呈对数变换关系,从理论上保证了所提算法的目标函数值小于标准PCA算法的。因为对标准PCA算法的目标函数采用了对数变换,大幅降低了异常样本对于目标函数值的影响,从而保证了所提算法的鲁棒性。理论分析表明,所提算法的每次迭代可以近似降低目标函数值,并且可以近似收敛于目标函数的最优解。 人脸数据集和手写字符数据集上的实验充分表明了所提算法的优越性。与现有的鲁棒PCA算法相比,所提算法对于异常样本的鲁棒性和处理能力有较大提升,取得了最低的重构误差并且取得了最高的识别率。与PCA-l2,p算法相比,所提算法的目标函数能够降低较小的重构误差,同时对于较大的重构误差有更强的抑制。与PCA-L1算法相比,所提算法保留了PCA算法具有的旋转不变性。实验分析表明,所提算法的收敛性能较好,一般迭代数次即可收敛,与理论分析一致。 未来可将对数变换应用于稀疏PCA算法,从而得到能更好地处理含有异常样本的稀疏PCA算法。2 对数变换的PCA算法
2.1 目标函数建立
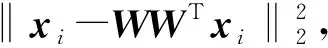
2.2 目标函数求解
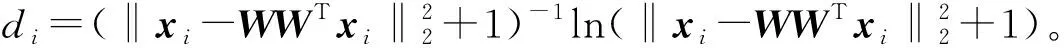
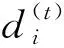
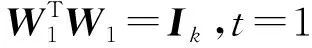
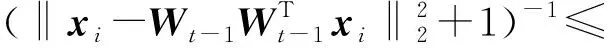
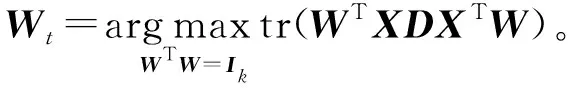
2.3 收敛性分析

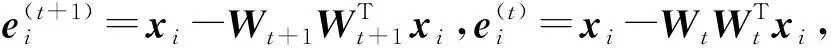
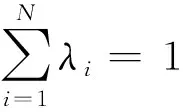
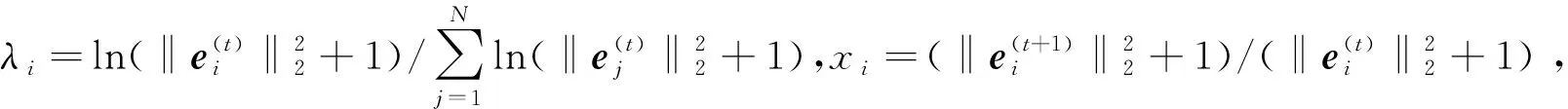
2.4 旋转不变性分析
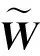
3 实验结果与分析
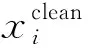
3.1 在AR数据集上的实验

3.2 在Extended Yale B数据集上的实验



3.3 在CMU PIE数据集上的实验



3.4 在MNIST数据集上的实验
3.5 收敛性实验
4 结 论
