容积伺服电液作动器位置控制研究

闫桂山,金振林

(1.燕山大学机械工程学院,066004,河北秦皇岛;2.河北省重型智能制造装备技术创新中心,066004,河北秦皇岛)

电液伺服技术作为工业装备制造领域的核心技术之一,在冶金、锻压、注塑、轨道交通等工业领域均有极其广泛的应用[1-2]。实现电液伺服技术与绿色发展、智能转型的有机结合,将极大推动我国工业的智能化进程[3-4]。以此为背景,越来越多的专家、学者致力于电液伺服技术与绿色智能理念的融合,电液伺服泵控技术便是其中一个重要研究热点[5-6]。容积伺服电液作动器是电液伺服泵控技术的典型应用,该电液作动器省去了庞大的液压站、复杂的管路系统以及昂贵的伺服阀,有效地克服了电液伺服阀控技术抗污染能力差、集成度低、能源浪费严重等技术缺陷,具有高效节能、高功重比和环境友好等技术优点[7-9]。

容积伺服电液作动器是一个多变量、强耦合、非线性和变参数的复杂系统,其中位置控制是其关键技术问题之一,在车辆悬架控制[10-11]、机器人关节驱动[12]和风力发电传动比调控[13]等工程领域均有重要应用。近年来,国内外学者对电液作动器的高精度位置控制问题做了相关研究。

国外Buchun等针对电液作动器动态变化的非线性问题,提出了自适应滑模控制方案,有效地解决了电液作动器的鲁棒性控制问题[14];Haris等针对电液作动器死区非线性问题,提出了一种鲁棒模型预测控制器,克服了测量扰动和非测量高斯扰动问题,提高了系统位置控制精度、鲁棒性和响应速度等[15];Chong等针对电液作动器轨迹跟踪问题,采用粒子群模糊逻辑控制器对系统进行位置控制优化,实现了在一定的范围内参考轨迹的准确跟踪[16]。

国内Li等针对电液作动器位置控制动态特性问题,采用提高电机输出扭矩、降低电机泵组转动惯量,以及采用双电机泵组结构等措施用以改善系统动态特性[17-18];Yang等提出一种新型滑模控制方法,具体包含降阶模型、扰动滑模观测器和自适应定律等,有效地改善了位置控制过程中的瞬态性能、稳态精度和鲁棒性[19-20];姜继海等针对电液作动器死区和非线性特征,采用基于趋近率的离散滑模控制算法,显著提高了系统位置跟踪特性[21]。

上述研究工作大多从电液作动器位置控制的非线性、死区、转动惯量等角度出发,随着控制精度指标要求的提高,从系统固有频率、阻尼比等动力学参数本质角度实现电液作动器位置控制有待进一步研究。本文针对电液作动器高精度位置控制问题,建立电液伺服作动器数学模型,提出三状态反馈与三状态顺馈控制策略,通过三状态反馈补偿系统固有频率和阻尼比,并利用三状态顺馈实现极点配置,进而对控制器进行参数优化设计,有效改善了系统的动态特性与控制精度。

1 电液作动器简介

容积伺服电液作动器主要包括伺服电机、定量泵、液压阀、蓄能器、液压缸和控制器等,其工作原理如图1所示。

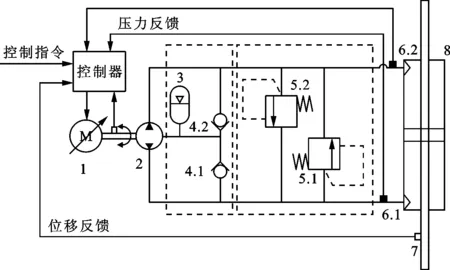
1—伺服电机;2—定量泵;3——蓄能器;4.1—A腔单向阀;4.2—B腔单向阀;5.1—A腔溢流阀;5.2—B腔溢流阀;6.1—A腔压力传感器;6.2—B腔压力传感器;7—位移传感器;8—液压缸。图1 电液作动器工作原理图

电液作动器采用伺服电机-定量泵-液压缸容积控制方案,定量泵吸排油口直接连接液压缸两负载油口A、B两腔;蓄能器配合单向阀实现系统补油功能;溢流阀实现系统压力过载保护;控制器采集系统压力、位移等状态信息,并输出控制指令,进而通过伺服电机实现电液作动器的闭环伺服控制。

2 数学模型

针对电液作动器核心元件伺服电机、液压泵和液压缸进行建模分析,以此为基础对电液作动器位置伺服控制系统进行研究。

2.1 伺服电机数学模型

电液作动器在进行位置控制过程中,伺服电机作为控制算法的执行终端,是位置控制的关键部件,其具体数学模型如下。

电机定子磁链方程

(1)

电机定子电压方程

(2)

电机电磁转矩方程

(3)

电机运动方程

(4)

式中:ψd、ψq为定子磁链的d-q轴分量;Ld、Lq为定子电感的d-q轴等效电感;id、iq为定子电流的d-q轴分量;ψf为永磁体磁链;Ud、Uq为定子电压的d-q轴分量;Rs为定子电阻;ωe为电机转子角速度;Te为电机电磁转矩;pn为电机极对数;TL为电机负载转矩;JL为转子轴等效折算转动惯量;ωm为电机的机械角速度;D为电动机阻尼系数。

2.2 液压泵数学模型

液压泵为电液作动器的动力元件,为液压缸运动提供液压动力输入。

液压泵流量输出方程为

Qp=Dpωp-CpPL

(5)

式中:ωp为液压泵角速度;Dp为液压泵额定排量;Qp为液压泵输出流量;Cp为液压泵泄漏系数;PL为负载压力。

2.3 液压缸数学模型

液压缸为电液作动器的执行元件,是电液作动器与负载作用的执行终端,其数学模型描述如下。

液压缸的流量连续性方程为

(6)

液压缸和负载的力平衡方程为

ApPL=mts2Xp+BpsXp+KXp+FL

(7)

式中:Ap为液压缸有效作用面积;QL为液压缸负载流量;Ct为液压缸总泄漏量;Vt为系统总压缩容积;βe为油液有效体积弹性模量;mt为活塞及负载折算到活塞上的总质量;Bp为活塞及负载的黏性阻尼系数;K为负载弹簧刚度;Xp为液压缸输出位移;FL为作用在活塞上的任意外负载力。

2.4 位置控制系统模型分析

由式(5)～(7)建立电液作动器位置控制的框图如图2所示。由图2可推导得到电液作动器位置伺服开环传递函数为

(8)

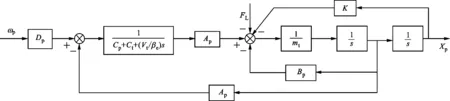
图2 电液作动器位置控制框图

式中:Kce为总流量-压力系数,Kce=Ct+Cp。

忽略黏性阻尼和负载的弹性,即Bp=0,K=0,将式(8)的三阶特征方程分解为一阶和二阶两个因子,可得

(9)

式中:ωh为电液作动器液压固有频率;ξh为电液作动器液压阻尼比。

进一步,ωh、ξh可表示为

(10)

3 控制方法研究

本文拟通过状态反馈与状态顺馈的方式,选取系统位置、速度和加速度3个物理状态,形成三状态反馈与三状态顺馈控制策略。通过补偿电液作动器固有频率与阻尼比,并配置闭环极点,进而提高系统的控制性能指标。

3.1 三状态反馈控制

电液作动器液压固有频率较低、阻尼比较小、系统稳定裕量低,无法快速精确跟随控制输入指令。为此,采用三状态反馈方法来补偿系统的固有频率和阻尼比,改善系统的控制品质。

三状态反馈控制的具体思想为:通过反馈矩阵E(s)对电液作动器位置伺服系统进行极点配置,规划传递函数G(s)的极点到期望位置,进而补偿系统固有频率和阻尼比,解决系统静态精度不高与动态性能受限问题,最终提高系统控制性能,控制原理如图3所示。

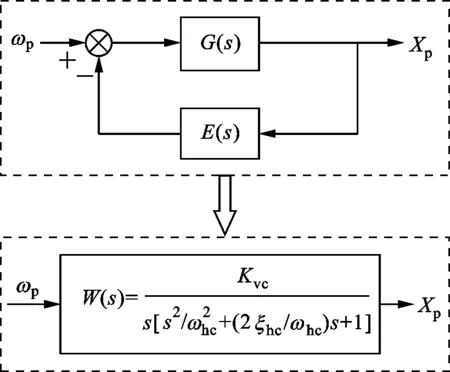
图3 三状态反馈控制原理图

由式(9)可知,电液作动器位置控制传递函数可简化为

(11)

其中Kv为开环增益,可表示为

(12)

设三状态反馈控制后,系统期望的闭环传递函数为

(13)

系统期望的闭环传递函数中ωhc和ξhc直接影响系统的控制特性,电液作动器控制指标从时域角度通常用超调量MP和峰值时间tp进行约束,其中MP≤5%,tp≤3 s,以此为边界条件,对期望的闭环传递函数中固有频率和阻尼比进行约束,可得

(14)

进一步,三状态反馈控制系统如图4所示。

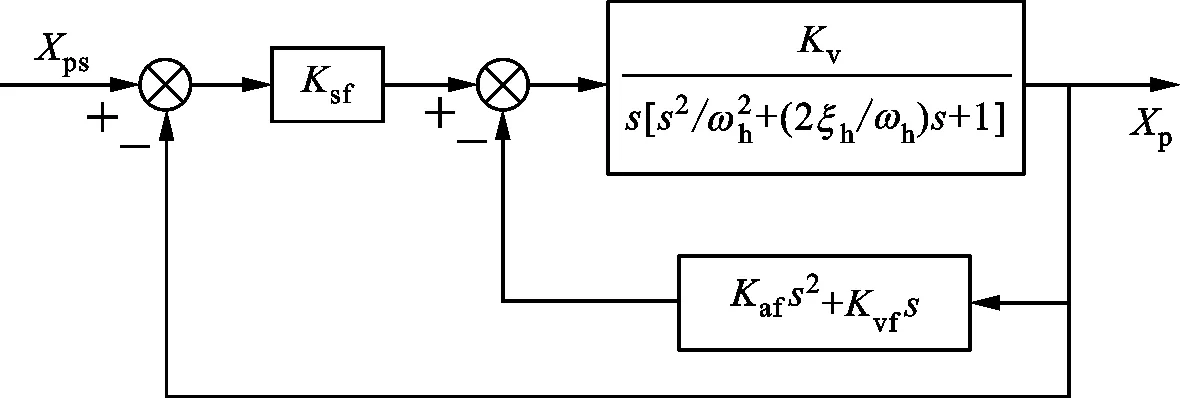
图4 三状态反馈控制系统框图

由图4可知,三状态反馈控制后,对应的系统期望的闭环传递函数可表示为

(15)

式(13)和(15)化为状态方程后,相应系数项相等,计算可解得

(16)

3.2 三状态顺馈控制

三状态反馈可使系统固有频率和阻尼比得到补偿优化,并将系统的主要极点控制到所希望的区域。在三状态反馈控制的基础上引入三状态顺馈控制策略,实现极点配置,可拓展系统频宽,进一步优化系统控制性能。

三状态顺馈控制的具体思想为:通过引入F(s)环节,在电液作动器位置闭环传递函数中,对消距离虚轴较近的主导极点,控制原理如图5所示。

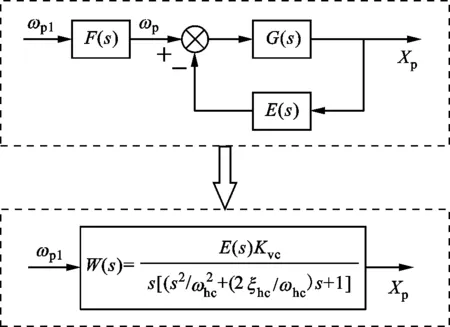
图5 三状态顺馈控制原理图

设F(s)有如下形式

F(s)=Ksv+Kvvs+Kavs2

(17)

进一步,用F(s)对消系统ωhc处极点,即令

(18)

式(17)和(18)联立,解得

(19)

4 实验研究

实验平台由伺服电机、液压泵、控制阀块、伺服缸和采集与控制系统组成,其中驱动器控制伺服电机实现液压泵的转速伺服控制,组成电动伺服泵单元,是电液作动器的核心部分,其组成构架如图6所示。

图6 电动伺服泵单元构架图

进一步,电动伺服泵单元安装在功能阀块上,并通过液压管路与执行机构液压缸相连接。电液作动器实验台如图7所示。

图7 实验台实物图

在Simulink中编译三状态反馈与三状态顺馈控制算法,并将控制算法下载到轴控制器中,轴控制输出控制指令Uref,进而实现实验平台的实时控制。电液作动器实验台电气控制部分如图8所示。

图8 实验台电气控制部分实物图

电液作动器实验平台工作参数如表1所示,电液作动器实验平台关键传感器技术规格如表2所示。

表1 实验平台工作参数

表2 关键传感器技术规格

给定电液作动器从240 mm运动到40 mm,得到实验曲线如图9所示。

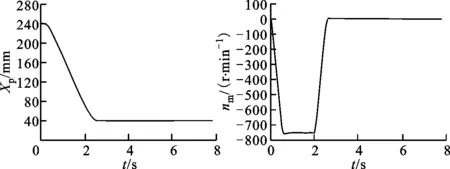
(a)液压缸位移(b)电机转速

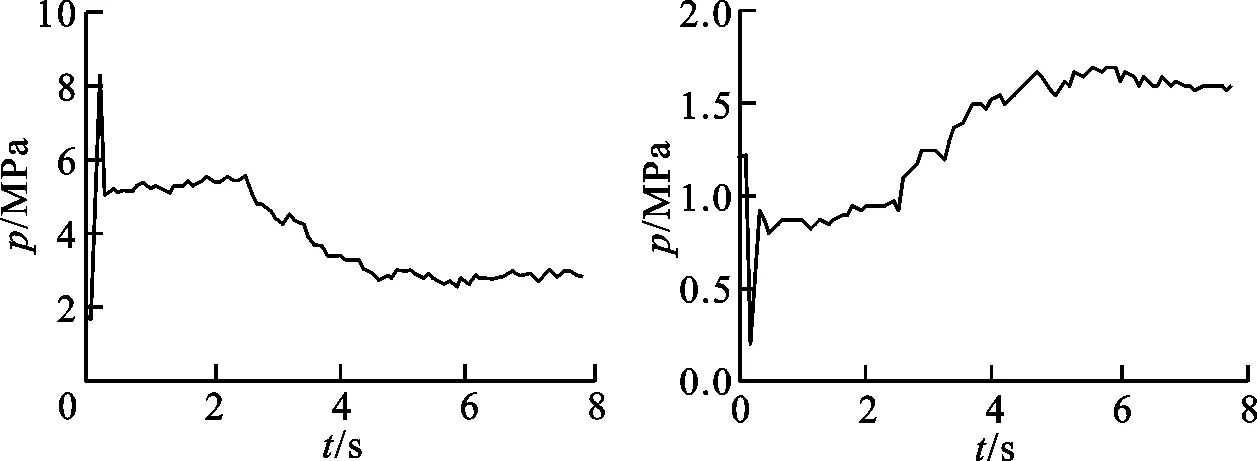
(c)A腔压力(d)B腔压力图9 电液作动器位移减小响应曲线

由图9可知,采用三状态反馈与顺馈控制策略,给定位移减小200 mm指令后,伺服电机转速和系统压力快速响应,电机转速峰值可达750 r/min,系统压力峰值高达8 MPa,液压缸位置在2.2 s内达到稳态位置,稳态精度为±0.01 mm。

给定电液作动器位移从40 mm运动到240 mm,得到实验曲线如图10所示。

(a)液压缸位移(b)电机转速

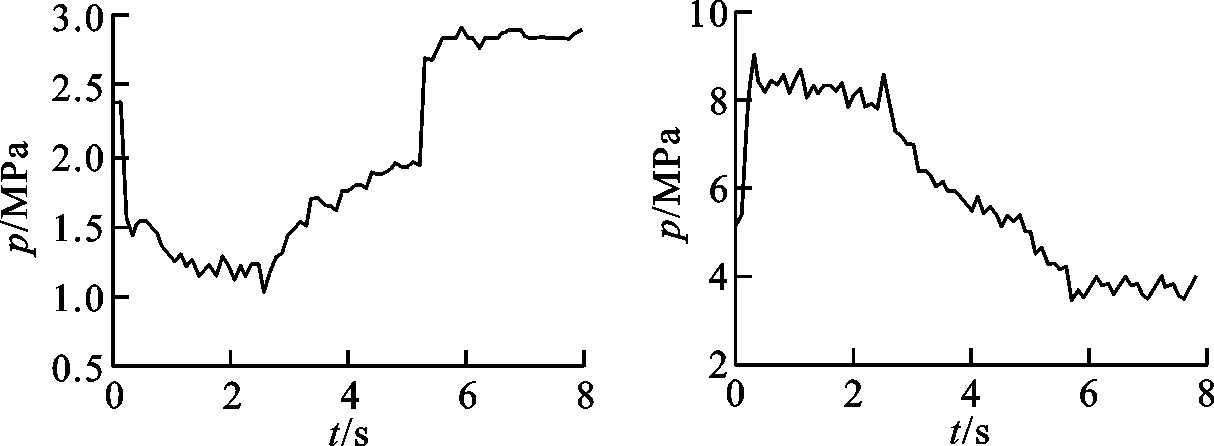
(c)A腔压力(d)B腔压力图10 电液作动器位移增加响应曲线

由图10可知,采用三状态反馈与顺馈控制策略,给定位移增加200 mm指令后,伺服电机转速和系统压力快速响应,电机转速峰值可达752 r/min,系统压力峰值高达9 MPa,液压缸位置在2.2 s内达到稳态位置,稳态精度为±0.01 mm。

为进一步验证所提出控制算法的动态特性,给定电液作动器位置指令幅值5 mm、频率2 Hz,所得实验结果如图11所示。

(a)位置跟随(b)控制指令图11 电液作动器位置动态跟随曲线

由图11可知,电液作动器液压缸位移可快速跟随位置指令,幅值偏差控制在±0.01 mm范围内,相位偏差控制在±0.1°范围内,具有良好的动态跟随特性。

5 结 论

针对电液作动器位置高精度问题,通过数学模型和实验分析,提出了一种三状态反馈与三状态顺馈控制策略,得到主要结论如下。

(1)建立了电液作动器位置伺服控制系统数学模型。

(2)提出了三状态反馈与顺馈控制策略,通过补偿电液作动器固有频率与阻尼比,并配置闭环极点对控制器参数进行设计,用于电液作动器位置输出高精度控制。

(3)实验分析表明,所提出的控制方法具有良好的控制效果,为电液作动器位置输出高精度控制奠定了一定的基础。