微型导弹纵向扰动抑制控制系统设计*

李 彤，孟志鹏，吕 良，张士峰

(1.军事科学院 国防科技创新研究院，北京 100071；2.国防科技大学 空天科学学院，湖南 长沙 410073)

微型战术精确制导武器是现代军事兵器发展的重点方向之一，也是未来军事智能无人作战体系的重要组成部分。在现代战争中和反恐战场上，为满足单兵高精度小附带损伤的灵活战术打击需求，保护士兵自身不受突发威胁影响，同时结合无人机和无人车等无人作战系统形成察打一体功能，便携式微型精确制导导弹得到了各国军方的广泛关注[1]。然而由于单兵手持发射及无人机载发射的扰动较大，其控制系统设计存在一定挑战。

近年来，扰动估计与抑制控制因其高精度和低成本特点受到广泛关注，许多学者从不同方面对该类方法进行了综述[2-5]，介绍了包括扰动观测器(Disturbance OBserver，DOB)控制、扩张状态观测器(Extended State Observer，ESO)控制、等效输入扰动(Equivalent-Input-Disturbance，EID)控制、未知输入观测器(Unknown Input Observer，UIO)控制、扰动估计器(Uncertainty and Disturbance Estimator，UDE)控制等多种控制方法。该类方法核心在于将控制系统性能和鲁棒性之间的设计矛盾分离成两个独立问题：控制器设计仅基于标称模型；观测器用于估计“集总扰动”，即实际模型与标称模型间的偏差和扰动。

然而，扰动估计与抑制控制方法在工程实践中仍存在诸多不足：①经典线性设计方法和频域分析因其简洁可靠在工程领域不可替代，且具有丰富设计经验，而现有的扰动估计与抑制控制方法研究大多集中于非线性方法和时域设计[6-8]；②很多扰动估计与抑制控制方法，如扩张状态观测器控制，无法充分利用系统建模信息，而是将系统转换为积分链形式，并将建模误差视为“集总扰动”一部分，因此难以满足扰动有界条件[4]；③实际系统扰动绝大多数是非匹配的，即不直接存在于输入通道，虽然较多研究致力于解决该问题，但均会使控制系统设计更为复杂和非线性[5,9]；④在非线性设计条件下，分离原理将不再适用，控制器和观测器的单独设计将无法保证系统稳定性。

针对以上问题，本文结合H∞综合和等效输入扰动理论，对扰动抑制估计与控制方法进行改进，从而应用于微型导弹纵向控制系统设计。H∞优化与综合在故障诊断识别与容错控制中应用广泛[10-12]，通过权函数设计将频域分析应用于故障和扰动的识别与估计，同时H∞鲁棒控制理论可以保证控制系统设计的稳定性。等效输入扰动理论则可以很好解决非匹配干扰问题，充分利用系统建模信息，且不依赖系统模型变换、全状态可用性或扰动先验信息[13-15]。两者的结合能够充分继承传统经典频域设计方法，同时，将扰动估计与抑制控制方法应用于微型导弹纵向控制系统设计，保证微型导弹飞行性能。

1 微型导弹纵向模型建立与变换

1.1 导弹纵向动力学建模

微型导弹飞行高度在近地面200 m以内，飞行马赫数为0.6左右，根据导弹动力学建模的刚化原理、小扰动假设、冻结系数及大地平面等基本假设[16-17]，导弹纵向动力学模型通过式(1)[18-19]进行描述。

(1)

式中：M代表马赫数；α代表攻角，单位为rad；q代表俯仰角速率，单位为rad/s；θ代表速度倾角，单位为rad；m代表导弹质量；IZ代表俯仰方向转动惯量；S代表弹体特征面积；D代表弹体特征长度；P0代表大气压力；VS代表声速；g代表重力加速度；CD0、Cn和Cm分别代表零攻角阻力系数、无因次法向力系数和俯仰力矩系数。

(2)

其中：ai，bi，ci，di(i=m,n)和em为常系数；δ为控制舵偏，单位为rad。

舵机执行机构视为一阶惯性系统。

(3)

式中，ωa为舵机带宽，δc为舵机控制指令。舵机舵偏及转速需满足如下非线性饱和约束：

(4)

表1给出了微型导弹相关参数取值。

将攻角作为系统输出和唯一观测量，将舵偏控制指令作为系统输入，即y=α，u=δc，由此保证系统输入输出的零动态稳定性[19]。在工程实践中，攻角值通过导航解算伪攻角获取。控制系统设计目标是令系统能够快速准确地跟踪攻角指令αc，同时具有较好的抗扰能力。

1.2 等效输入扰动系统建立

标准的单输入单输出非线性系统如下：

(5)

其中，h(x,u)表示系统内外扰动和不确定性。

假设该系统表示为特征点上的线性化形式如下：

(6)

其中，f(x)=Ax+Δf(x)，g(x)=B+Δg(x)。

则定义一个相对系统如下：

(7)

这里需对以上两个系统状态空间做如下假设：

假设1系统矩阵(A,B)能控，(A,C)能观。

假设2系统矩阵(A,B,C)在虚轴上没有零点。

假设1是控制系统设计的基本要求，即所研究对象为常规系统；假设2则是确保系统稳定的必要条件。若对于所有t>0，系统输出均满足y(t)≡y′(t)，则称d(t)为等效输入扰动，系统(7)则称为系统(5)的等效输入扰动系统。为做进一步补充说明，这里需给出引理1[13]。

引理1令

Φ={pi(t)sin(ωit+φi)}i=0,1,…,n;n<∞

(8)

式中，ωi(ωi>0)和φi为常数，pi(t)代表关于时间的任意多项式。在假设1和假设2成立的条件下，如果系统(6)输出轨迹在Δf(x)+Δg(x)u+h(x,u)作用下属于Φ，则在系统控制输入通道上一定存在一个匹配的等效输入扰动，使得系统(7)产生相同的输出轨迹。

根据傅里叶分析可知，绝大部分实际系统的输出信号满足狄利克雷条件，即连续有界条件，均能通过傅里叶变换而属于Φ，因此，引理1保证了实际应用中等效输入扰动的存在性。从而建立等效输入扰动系统，并根据系统输入输出对扰动进行估计。值得注意的是，等效输入扰动系统与原系统是不同的，仅针对系统输入输出，即除了y′(t)≡y(t)，其余状态与原系统状态均不相同，也没有任何物理意义。

对于式(1)～(3)，选定系统状态为x=[α,q,δ]T，从而将系统线性化，并转换为如式(9)所示的包含等效输入扰动的状态空间模型。

(9)

显然，系统状态空间矩阵(A,B,C)满足假设条件。由此，完成微型导弹纵向等效输入扰动系统建模。

2 微型导弹鲁棒纵向控制系统设计

为将经典频域设计方法应用于微型导弹纵向扰动抑制控制设计中，引入H∞鲁棒控制，并结合等效输入扰动理论，以提高经典控制系统设计性能。

2.1 H∞扰动滤波器设计

根据上文所建立的微型导弹等效输入扰动系统，可得系统传递函数为：

G(s)=C(sI-A)-1B

(10)

基于此设计扰动滤波器对等效输入扰动进行估计和补偿。扰动滤波器H∞回路结构如图1所示，H(s)即为所设计扰动滤波器，Wu(s)为施加在系统输入上的权重，通常代表执行机构模型。扰动滤波器的H∞综合主要通过Wd(s)和Wed(s)两个权函数对系统频域性能进行规划。权函数利用频域设计经验和信息进行设计，分别对等效输入扰动及其观测误差加权约束，以实现鲁棒快速准确的扰动估计性能。Wact(s)代表执行机构对输入信号的限制约束，且Wact(s)=[Wacts(s),Wactr(s)]T，Wacts(s)和Wactr(s)分别为执行机构幅值约束和速率约束权函数，体现了扰动补偿在输入通道内的限制。由此，扰动滤波器求解问题转化为若干性能指标以进行优化综合。

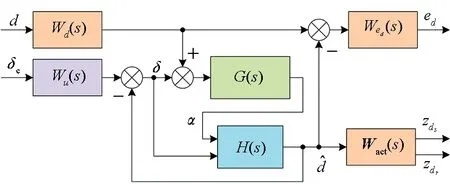
图1 扰动滤波器H∞回路结构Fig.1 H∞ interconnection of disturbance filter

扰动滤波器的回路结构关系描述为：

(11)

其中，

(12)

扰动估计值表示为：

(13)

通过对增广系统P(s)进行线性分式变换(Linear Fractional Transformation，LFT)Fl(P,H)，可得：

M(s)=Fl(P,H)

=P11(s)+P12(s)[I-H(s)P22(s)]-1H(s)P21(s)

(14)

从而可得扰动观测误差为：

(15)

对于系统输入约束的权函数Wu(s)和Wact(s)，在舵机模型基础上进行设计。其中，Wu(s)由于代表执行机构对输入的作用，直接选取舵机模型；而Wact(s)反映了舵机对舵偏和转速的非线性约束，通过幅值限制方式对其进行设计。因此，系统输入相关权函数设计如下：

(16)

其中，Gact(s)舵偏可达到的最大幅值和最大转速。对于扰动估计相关权函数Wd(s)和Wed(s)，采用如式(17)所示权函数设计形式。

(17)

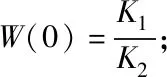
(18)

而后通过对式(19)进行H∞综合优化求解，可得扰动滤波器H(s)。

(19)

由此可知，不同于其他扰动估计方法，以上设计方式直接将频域分析与设计方法通过权函数设计应用于扰动观测和估计，并获得预期性能，同时，H∞优化也保证了滤波器稳定性。

2.2 H∞复合控制器设计

为实现稳定的跟踪性能，复合控制器设计需考虑包含扰动滤波器在内的全系统，从而形成闭环反馈跟踪控制。H∞复合控制器回路结构如图2所示，其中K(s)为需要设计的复合控制器，而H(s)则代表已知的完成设计的扰动滤波器，可见复合控制器设计是在包含扰动滤波器的整体系统基础上，通过设计跟踪误差权函数We(s)而实现对复合控制器的H∞综合优化。由We(s)对跟踪误差进行性能规划约束是H∞控制器设计的典型特征，但与常规鲁棒控制不同的是，H∞回路结构中并没有考虑不确定性，这是由于扰动滤波器所估计的等效输入扰动已包含系统不确定性，并且会通过输入通道进行补偿。

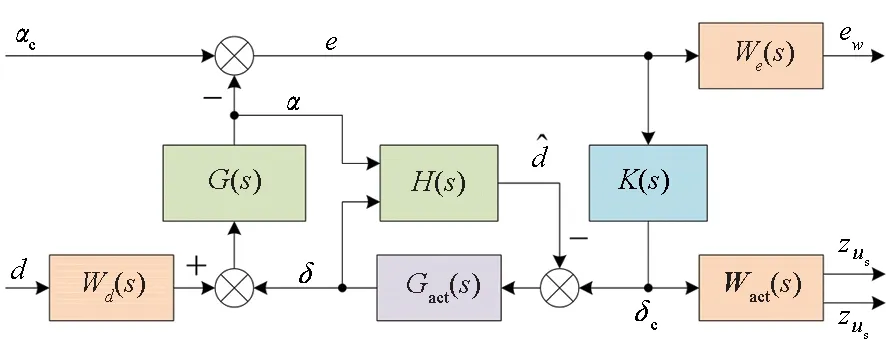
图2 复合控制器H∞回路结构Fig.2 H∞ interconnection of composite controller

复合控制器的回路结构关系描述为：

(20)

其中，

(21)

类似于扰动滤波器设计，通过对增广系统Q(s)进行下LFT，即Fl(Q,K)，可得：

N(s)=Fl(Q,K)

=Q11(s)+Q12(s)[I-K(s)Q22(s)]-1K(s)Q21(s)

(22)

从而可得跟踪误差及输入信号关系：

(23)

复合控制器闭环带宽通常取为扰动估计误差权函数Wed(s)带宽的1/10，即跟踪误差权函数We(s)带宽ωR取5 rad/s，为保证足够的跟踪性能，K1和K2取值分别为100和10，以实现对控制带宽内的低频带较大加权，对高频带较小加权。因而可得跟踪误差权函数为：

(24)

通过对式(25)进行H∞综合优化求解，可得复合控制器。

(25)

考虑到工程要求，在优化求解后，H∞扰动滤波器和复合控制器均按照实际应用进行降阶处理，以实现简化目的。

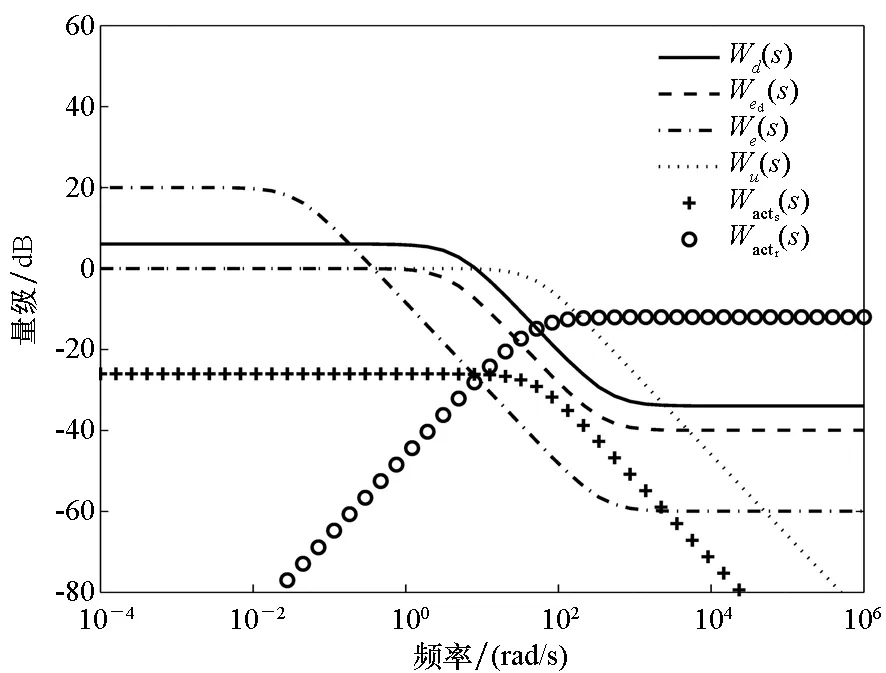
图3 设计权函数频域响应Fig.3 Frequency responses of designed weight functions

3 数值仿真验证

3.1 标称系统仿真分析

3.1.1 标称系统频域仿真

根据所设计的微型导弹纵向控制系统，首先针对线性标称系统的频域响应进行仿真分析。在H∞扰动滤波器和复合控制器作用下，系统闭环频域特性曲线如图4所示。

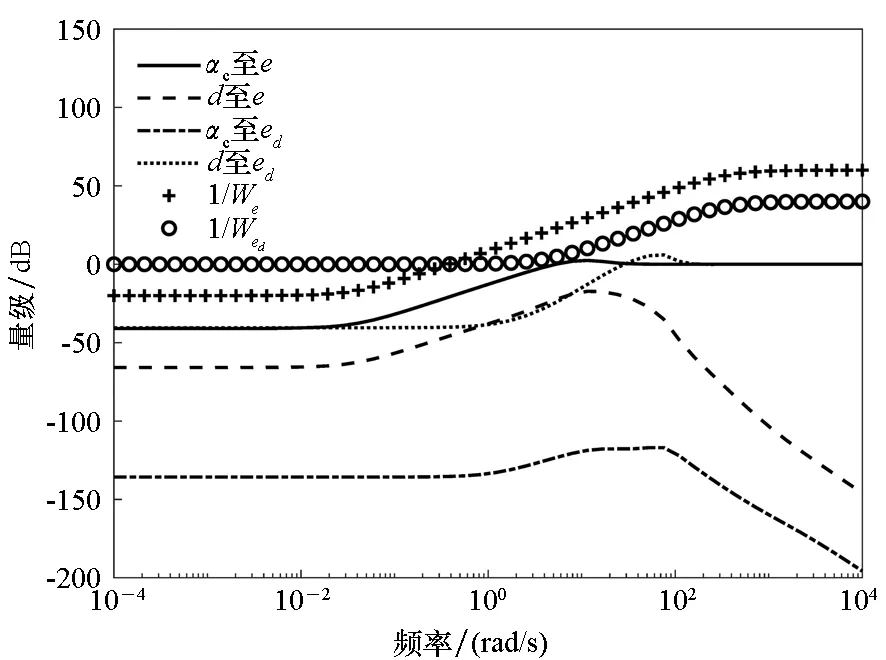
图4 闭环系统频域特性曲线Fig.4 Frequency responses of closed-loop system

由图4可知，扰动滤波器和复合控制器设计均位于权函数设计约束内，频域响应幅值均在权函数之下，且设计裕度较大，同时扰动d至扰动估计误差ed和参考指令αc至跟踪误差e的带宽也满足相应权函数设计需求，扰动滤波器带宽大于复合控制器。参考指令αc至扰动估计误差ed和扰动d至跟踪误差e的幅值均小于0，满足了扰动估计与闭环控制交叉影响较小的要求。

3.1.2 标称非线性系统时域仿真

系统标称非线性模型仿真基于MATLAB/ Simulink进行，积分计算方法采用定步长Runge-Kutta法，步长为1 ms。仿真起始条件为：M0= 0.7，α0= 0，q0= 0，θ0= 0，δ0= 0。攻角跟踪指令设计为：

(26)

微型导弹纵向控制系统标称非线性系统仿真结果如图5所示。在图5(a)中，攻角跟踪较为快速和精确，稳定时间约为0.7 s无超调，验证了控制系统设计的有效性。由马赫数、俯仰角速率和速度倾角曲线可知，跟踪过渡过程稳定，所设计的控制系统性能成功克服了系统非线性动力学和执行机构非线性约束。此外，图5(f)中的等效输入扰动估计也反映出系统非线性动力学参数变化。值得注意的是，为实现较高跟踪精度，等效输入扰动补偿对控制面偏转有较大影响。综上，仿真结果在理论上充分论证了控制系统设计方法在标称系统非线性动力学影响下的有效性。

图5 标称非线性系统仿真曲线Fig.5 Simulation results of nominal nonlinear system

3.2 性能对比分析

为进一步验证所设计的控制系统的性能，本节将选取扰动估计方法中经典的扩张状态观测器控制方法和扰动观测器控制方法进行对比分析。在文献[19]中，扩张状态观测器方法已通过与反馈线性化、预测控制和滑模控制的对比表现出更好的性能优势。因此，选取上述两种设计方法进行对比具有说服力和可行性。下面将对两种方法进行简要介绍。

3.2.1 扩张状态观测器控制方法

扩张状态观测器控制方法主要基于文献[19]。系统纵向模型以攻角微分形式进行反馈线性化，并根据小扰动假设，将系统动力学表示为：

(27)

式中，dESO为系统扩张状态，代表系统的“集总扰动”，扩张状态系统采用积分链形式。

(28)

e=αc-α

(29)

设计系统闭环跟踪动态特性为：

(30)

式中，m1，m2和m3为闭环反馈增益，通过将系统闭环动态特性极点设计为3/τc获得(τc=0.2)。将扩张状态观测器极点设计为4/τo(τo=τc/60)。最终可得扩张状态观测器控制方法的控制律为：

(31)

3.2.2 扰动观测器控制方法

扰动观测器控制方法主要采用文献[20]的传统线性设计方法。该方法的扰动估计主要通过系统输出做系统逆变换后的计算输入与系统实际输入的差值获取。一般应用滤波器将扰动估计限制于适当频段内，同时保证扰动估计传递函数的有理性。对于所建立的等效输入扰动系统，将扰动滤波器和低通滤波器等效为降阶扩张状态观测器，系统观测状态为：

(32)

类似地，观测器极点配置为4/τ′o(τ′o=τc/5)。控制器设计独立于观测器设计，采用经典单位反馈和常值前馈增益。假设单位反馈C(s)和系统G(s)表示为如式(33)所示的传递函数形式。

(33)

其中，NG(s)和DG(s)为互质的。极点配置问题即转换为求解特征多项式F(s)。因此，总的闭环传递函数为：

(34)

式中，p为前馈增益。系统闭环极点设计为5/τc。前馈增益设计需满足GCL(s)s=0=1。

最终可得扰动观测器控制方法的控制律为：

(35)

3.2.3 频域对比分析

图6给出了3种控制器设计的频域响应特性对比。由图6(a)可以看出，除了超低频(<0.1 Hz)外，3种控制器均在主频带内拥有类似的闭环频域响应。相对于其他两个控制器，H∞等效输入扰动控制器在低频带具有常值幅值特性是由权函数设计引起，对闭环系统动态特性没有明显影响。另外，在图6(b)中的控制器扰动估计频率响应中，幅值特性在达到高频带时略有不同。通过频域响应对比，3个控制器带宽相对一致，说明了3种方法在设计上的可行性。然而，应注意到图6中H∞等效输入扰动控制器从低频域到高频域的过渡过程比其他两个控制器更快，这是因为通过权函数设计优化能够精确地将扰动估计与高频干扰分开，这种细微差异将在下一步时域仿真对比中表现出更加显著的性能区别。

(a) 闭环频域响应曲线(r至e)(a) Frequency responses of closed-loop dynamics (r to e)

3.2.4 时域对比分析

时域对比分析采用拉偏数值仿真的形式，同时考虑扰动和不确定性，主要设计以下4种情形：

1)仅涉及气动不确定性，考虑+30%cn和+30%cm；

2)考虑气动不确定性+30%cn和-30%cm，同时，在输入通道中引入风干扰作为外部扰动，将其建模为幅度为8°且频率为0.25 Hz的正弦信号；

3)考虑气动不确定性-30%cn、+30%cm和风干扰，且考虑舵机非线性特性和不确定性，除饱和及限速特性外，将引入10 ms舵机响应延时、0均值1°标准差1 ms采样频率舵偏噪声以及-30%舵机带宽ωa；

4)考虑气动不确定性-30%cn、-30%cm、风干扰和舵机特性，同时考虑传感器噪声，引入0均值0.1°标准差1 ms采样频率攻角观测噪声。

时域拉偏对比仿真结果如图7所示。在图7(a)中，3种控制器均具有较好跟踪性能，在正向气动偏差下，鲁棒性较好，其中扰动观测器控制器上升时间比其他控制器短，但也存在一定超调，说明控制能力存在冗余。在图7(b)中，由于负向力矩系数偏差和风干扰，各控制器过渡过程均存在较小振荡，扩张状态观测器控制器受影响最小，因为其在设计中具有较大控制力矩冗余，而另外两个控制器控制效率则略有下降。在图7(c)中，负向气动力偏差执行机构特性对扩张状态观测器控制器产生显著影响，存在较大振荡，而其他两个控制器几乎不受影响，说明时域设计虽保证了较好的跟踪性能，但在执行机构非线性尤其舵机带宽下降条件下，鲁棒性较差，无法实现预期的控制性能。在图7(d)中，扩张状态观测器控制器已经发散，其积分链结构放大了传感器噪声对扰动估计的影响，而扰动观测器控制器跟踪过程也存在较大振荡，在负向气动作用偏差下对噪声较为敏感，因此，两种方式在实际工程应用中仍存在一定局限性。然而，H∞等效输入扰动控制器却表现出较强的扰动抑制能力，通过权函数设计的扰动估计能够精确地分离高频干扰，使其能够在工程实践中拥有较高应用价值。

(a) 考虑+30%cn和+30%cm(a) +30%cn and +30%cm considered

尽管H∞等效输入扰动方法在对比分析中得到验证且具有一定优势，但目前线性扰动抑制控制方法中稳定性分析所依赖的扰动边界假设，在工程实践中仍需进一步拓展。另外，该设计方法在H∞综合中需满足系统矩阵要求的局限性，将在下一步工作中针对更为复杂的应用情形进行讨论。

4 结论

本文研究了一种基于H∞综合和等效输入扰动的微型导弹纵向控制系统设计方法。该方法在继承传统频域设计经验的同时，引入了扰动抑制提高控制系统鲁棒性，并通过频域和时域分析以及拉偏对比仿真，充分验证了该方法在非线性、扰动及不确定性等条件下的有效性以及较好的跟踪性能。扰动边界条件以及H∞系统矩阵局限性要求将在下一步工作中进行讨论。对于复杂时变系统的工程应用和飞行试验，将结合增益调度和线性时变参数系统技术，在未来进行更为深入的研究。