适应任务的模块化卫星快速构建优化决策方法*

陈 浩，彭 双，杜 春，伍江江

(国防科技大学 电子科学学院，湖南 长沙 410073)

面向突发安全事件、灾害应急救援等的航天应急观测、应急通信保障、应急高精度导航任务具有突发性、短暂性和局部性的特点[1]。传统的航天系统通常以特定的长期服务为设计目的，临时调整其服务范围技术复杂、成本昂贵，难以对上述的应急航天任务提供有效支持。

因此，快速响应空间(Operationally Responsive Space,ORS)[2]的概念应运而生，并得到了各航天大国的高度重视。快速响应空间的核心理念在于通过低成本、低风险的模块化小卫星快速组装，快速测试，按需应急发射，并完成应急组网，从而有效完成各项应急航天任务。美国先后发射了Jumpstart、ORS-1、TacSat-3、TacSat-4、ORS-4和ORS-5等卫星以验证ORS相关关键技术[3]。快速响应空间技术体系涉及面较广，目前主要的研究工作集中在ORS技术体系[3-4]、ORS卫星标准化模块制造[5]、ORS卫星应急部署与组网[6]、ORS卫星在轨任务调度[7-9]、ORS卫星运控系统及应用[10-12]等方面。

随着ORS技术的不断发展与应用的不断深入，应急航天任务对卫星集合能力的要求不断细化，卫星平台与有效载荷的型号和种类也在大幅增加。于是一个新且亟待解决的问题逐渐引起了人们的关注：面向一系列的应急航天任务，如何从型号众多、能力各异的标准化卫星平台及有效载荷中快速决策出优化的卫星装配方案，在最低限度满足所有应急航天任务的前提下，使得效费比最佳。这个问题是适应任务的模块化卫星快速构建优化决策问题。目前，对该问题的研究工作较少，尚不成体系。祝周鹏[13]对ORS卫星平台及载荷配置问题进行了研究，建立能力树模型，并采用标准遗传算法进行求解，但算法参数不能根据计算过程进行自适应调整，求解结果优化程度尚有提升空间。

本文在深入分析适应任务的模块化卫星快速构建优化决策问题的基础上，建立约束满足问题模型，提出基于自适应罚函数遗传算法的优化决策方法，并通过实验证明所提方法的可用性及有效性。

1 优化决策模型

1.1 问题描述

面向需要被响应的应急航天任务集合T_Set，通过选择标准模块方式，快速构建卫星集合S_Set，需要通过优化决策方法生成一个构造方案Plan，使得S_Set有能力最低限度完成所有T_Set中的应急航天任务，且方案效费比η最高。具体包括：

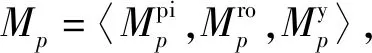
4)优化决策的结果是形成卫星集合S_Set的构造方案Plan。即选定卫星平台的种类和数量，以及有效载荷的种类和数量，并分配哪些有效载荷搭载于哪个卫星平台之上，从而形成面向航天应急任务T_Set的卫星集合S_Set。对于∀s∈S_Set，s=〈ps,d_Sets〉。其中，ps∈Plat_Set，d_Sets⊂Pyld_Set，分别表示卫星s采用的卫星平台和该平台携带的载荷集合。

1.2 模型建立

在适应任务的卫星快速构建优化决策问题中，优化目标是使方案效费比η最大化。

任务集合的执行效果可定义为：

(1)

即任务集合总体执行效果为任务集合中所有个体任务执行收益之和。

任务集合的执行代价是模块化卫星集合的制造代价，可表示为：

(2)

式中，ps∈Plat_Set，d_Sets⊂Pyld_Set，ps和d_Sets分别表示卫星s采用的卫星平台和该平台携带的载荷集合。

则本问题的优化目标可表示为效费比的形式，即：

(3)

适应任务的卫星快速构建优化决策过程还需要满足如下约束条件。

1) 任务最低限度满足约束(C1)。根据应急航天任务集合T_Set构造出的卫星集合S_Set具有最低限度完成T_Set中所有任务的能力。

(4)

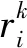
2)卫星平台装载能力约束(C2)。对每一颗卫星而言，卫星平台搭载的载荷不能超过该卫星平台装载能力上限。

对于∀s∈S_Set,有：

(5)

3)卫星平台质量约束(C3)。对每一颗卫星而言，卫星平台及搭载载荷的总质量不能超过单颗应急响应卫星质量上限。

对于∀s∈S_Set,有：

(6)

式中，ΔWSS是单颗应急响应卫星质量上限。

4)卫星能量供应约束(C4)。对每一颗卫星而言，该卫星搭载的载荷同时工作所消耗的总能量不大于该卫星平台所能提供的能量的上限。

对于∀s∈S_Set,有：

(7)

式中，0<μps≤1，μps为卫星平台ps上所有载荷同时工作的能量复用因子。

2 基于遗传算法的优化决策方法

上述数学模型是一个典型的约束满足问题模型(constraint satisfaction problem model)。需要在考虑C1～C4等约束条件的基础上寻找费效比η最大的卫星集合构造方案。如果只考虑约束条件C2、C4和优化目标函数，面向任务的模块化卫星快速构建优化决策问题可以归约到多维0-1背包问题。依据算法复杂性理论[14]，多维0-1背包问题是经典的NP难(NP-hard)问题，目前尚没有多项式时间快速算法。由于考虑更多约束条件，面向任务的模块化卫星快速构建优化决策问题组合爆炸特征更加明显。如果需要在有效时间内，从上百种标准化卫星平台以及几百种模块化载荷中快速计算出适应特定任务集合的卫星构造方案，基于穷尽搜索技术的精确算法难以满足要求。

为了在有限的空间和时间内得出问题优化解，拟采用元启发式算法(meta-heuristic algorithm)对该模型进行求解。

遗传算法是模拟自然界生物繁衍、进化过程的元启发式算法。已经广泛运用于复杂的函数极值问题、组合优化问题、规划调度问题等问题的求解[15]。文献[16-18]将进化计算运用到航天任务规划调度领域，取得了较好的效果。

针对面向任务的模块化卫星快速构建优化决策问题特点，提出基于自适应罚函数遗传算法的模块化卫星快速构建优化决策方法(optimization Decision Algorithm for Task-oriented modular Satellite rapid Construction,DA4TSC)。遗传算法中个体适应值采用效费比η。下面将介绍问题编码及遗传算子设计。

2.1 问题编码

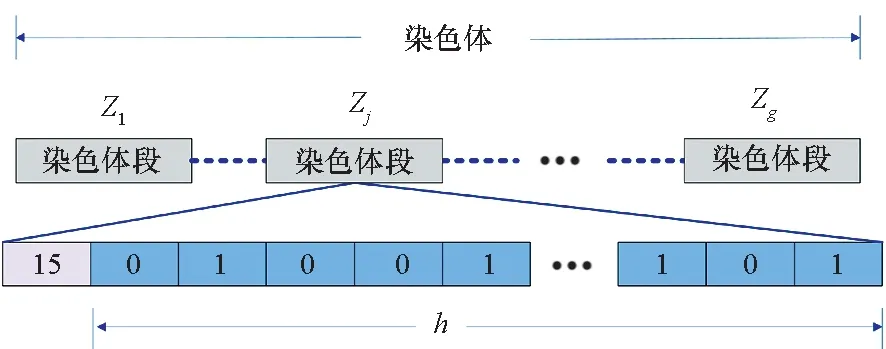
图1 问题编码示意Fig.1 Illustration of problem coding

2.2 交叉算子设计

针对适应任务的模块化卫星快速构建优化决策问题编码特点，设计了多点交叉算子(Crossover)。多点交叉算子在每颗卫星构造方案中选择一个交叉点基因进行交叉操作，如图2所示。通过轮盘赌方式选出父代个体1，染色体被选中的概率和其适应值大小成正比。采用随机选择方式得到父代个体2。

图2中假定当前染色体包含5个染色体段(即5颗卫星的构造方案)，对每一个染色体段生成一个交叉点，实现基因多点交叉互换操作。

图2 交叉算子操作示意Fig.2 Illustration of crossover operation

2.3 变异算子设计

变异算子(Mutation)设计为“随机扰动+随机爬山”的组合方式。随机扰动是指随机选择一个属于某颗卫星方案的基因位，然后对该基因位随机指定一个合法的值。由2.1节可知，基因位分为描述卫星平台使用情况的基因位和描述卫星有效载荷使用情况的基因位。值得注意的是，两类基因位将以不同概率分别进行随机扰动操作。如果某颗卫星构造方案进行了随机扰动，则对该卫星构造方案进行随机爬山操作。随机爬山操作是指针对该卫星构造方案中选定的卫星平台，随机将新的载荷加入方案中或去掉方案中已有载荷，如果适应值提升，则采用新的构造方案；否则，保持随机扰动后生成的方案。随机爬山算法只能接收比当前解更加优化的解，而无法接收优化性不如当前解的解，容易使得算法陷入局部最优解。而随机扰动算法是一种无偏的扰动方法，能够增加算法跳出局部最优解的概率，同时使算法在更大范围内的解空间中进行搜索。变异算子设计为上述两种算法的混合，既能够提升解的优化性，又能降低搜索过程陷入局部最优无法跳出的概率。

2.4 选择算子设计

在选择算子(Selection)设计中，采用含精英解池的轮盘赌选择算子。子代个体种群由两部分构成。第一部分是通过轮盘赌选择算子从父代种群中随机选择，适应值大的个体被选中概率更大。另一部分则是精英解池中全部个体。精英解池保存着当前种群发现的若干最优秀个体。随着遗传算法的运行，精英解池中的个体也在不断更新。

2.5 DA4TSC算法框架

基于上述问题编码和遗传算子设计，提出DA4TSC算法框架，见算法1。DA4TSC算法的输入包括应急航天任务集合T_Set和卫星数量g等两个变量，输出则是模块化卫星集合S_Set。

算法1 DA4TSC主要步骤Alg.1 Main steps of DA4TSC

由于需要构造的卫星数量g与航天应急运载能力、卫星投放方式等密切相关，并不仅仅由效费比决定，所以卫星数量g作为模型超参数直接输入算法中。DA4TSC中，语句③～⑦分别使用交叉算子、变异算子和选择算子对种群进行操作，模拟生物种群进化过程。语句⑤用于处理约束C1～C4导致的不可行解。语句⑥计算每一个个体的适应值。

3 基于领域知识的自适应罚函数约束处理机制设计

3.1 基于罚函数的遗传算法约束处理方法

由于约束条件C1～C4的存在，遗传算法种群中个体经过交叉、变异和选择算子后必然会生成部分不可行解。所以，需要采取约束处理方法对算法种群中的不可行解进行处理，使其可行化、部分可行化或向可行化方向转化[14]。

目前，在遗传算法处理约束优化问题的研究中，罚函数法是较普遍采用的约束处理方式之一[15]。罚函数法最早应用于数学优化方法的约束处理过程中。大量研究表明，最优解通常出现在可行解域与不可行解域的边界上[14]。在遗传算法的进化过程中，一个不可行解包含的染色体片段信息可能比可行解中的染色体片段信息更接近最优解。因此，罚函数法与遗传算法的随机搜索特性能够较好地结合，使得搜索过程能够从可行解域和不可行解域两个方向逼近优化决策问题的最优解。

在适应任务的模块化卫星快速构造优化决策问题中，共有C1～C4 4个约束条件。与应急航天任务和卫星集合能力匹配相关的是约束C1，与卫星平台及载荷匹配相关的约束是C2～C4。采用罚函数方法来处理约束时，可将其统一考虑。DA4TSC中，罚函数设计为将染色体违反约束C1～C4的总量的相反数乘以惩罚系数cp(cp>0)作为惩罚项。经罚函数方法修正后的个体适应值见式(8)。

(8)

其中，Fitness为修正后的染色体适应值，η为效费比，Vpty为染色体违反约束C1～C4总量的量化值，cp(cp>0)是惩罚系数。

由式(8)可知，加入罚函数方法后，则某个体的最终适应值为费效比η与其惩罚项之和。如果个体没有违反任何约束，则惩罚项为0。显然，惩罚项小于等于0。

3.2 自适应惩罚系数的引入

使用罚函数法进行约束处理的难点在于惩罚系数的设置[15]。如果惩罚系数设置较小，种群中个体违反约束的成本降低，遗传算法能够在更大的解空间中搜索问题优化解。同时，也会导致种群中不可行解数量增加，遗传算法收敛速度变慢。相反，如果惩罚系数设置较大，个体受到的惩罚力度增加，违反约束个体的适应值将大幅下降，导致算法搜索范围主要集中于可行解域，算法陷入局部最优解从而早熟收敛的概率也会增加。

相关研究表明：惩罚系数的合理取值范围不仅与问题特性及任务分布特点有关[15]，还与算法运行的阶段联系紧密。在遗传算法运行的初始阶段，需要将惩罚系数设置为一个较小的数值，使得算法能够搜索更大的解空间范围。而在遗传算法即将结束的阶段，则应当加大惩罚力度，使得种群中有尽量多的可行解。此外，当搜索过程长时间没有发现更好的解时(可能已经陷入局部最优)，则应调小惩罚系数，加大算法跳出局部最优解的概率。同理，如果算法种群中存在大量违反约束程度较多的不可行解，则应调大惩罚系数，引导算法搜索方向到可行解域中。

基于上述分析，设计了罚函数惩罚系数自适应机制，如图3所示。进化过程中，算法依据种群当前状态在算法运行阶段自适应调整惩罚系数，从而控制约束处理(constraint handling)步骤中惩罚力度的大小，从而引导算法在最有希望获取问题优化解的区域进行搜索。

图3 自适应惩罚系数调整示意Fig.3 Illustration of the penalty coefficient adaptive adjustment for penalty function method

自适应惩罚系数cp(λ)动态变化方式为：

(9)

其中：λ表示当前进化代数；case#1 表示当前种群中最优个体已经连续h代为不可行解，或最优个体已经连续h代没有变化(可能陷入了局部最优)；case#2表示当前种群中最优个体已经连续h代为可行解；θ1、θ2为变化参数，0<θ1,θ2<1，且θ1≠θ2(防止循环)；cgen(λ)是进化罚系数，其随着DA4TSC进化迭代过程的进行而不断增加，可表示为如式(10)所示的递推关系式。

cgen(λ+1)=cp(λ)+cstep

(10)

式中，cstep是进化迭代步长，可表示为：

(11)

式中：cp(0)是初始惩罚系数；λmax是DA4TSC最大迭代次数；cmax是预设惩罚系数上限，cmax可根据经验估计得到。

4 实验及分析

采用随机生成方式，产生应急航天任务集合，并构造不同规模的测试用例16组，如表1所示。

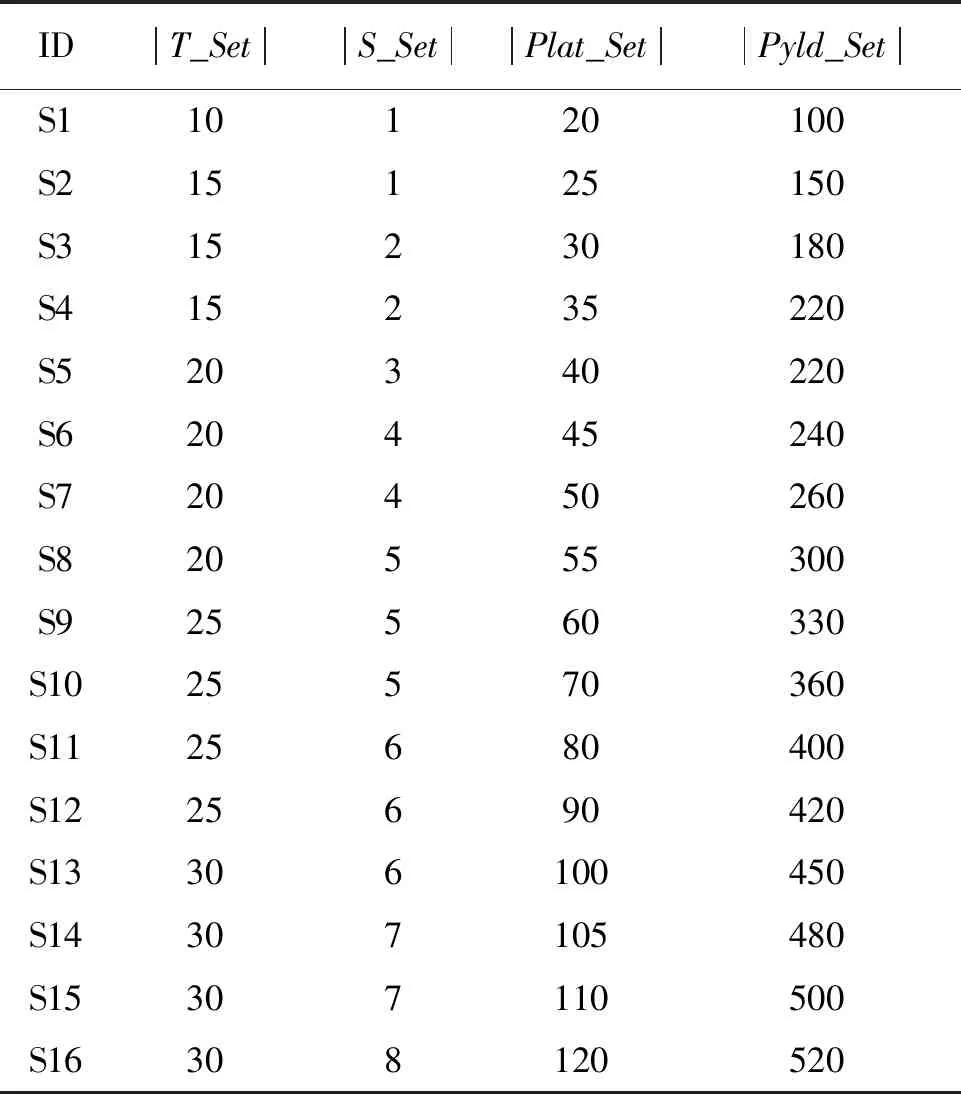
表1 实验数据说明Tab.1 Description of experimental data

其中，ID是实验用例唯一标识，|T_Set|为应急航天任务数量，|S_Set|为需要构造的卫星数量，|Plat_Set|为备选的卫星平台集合，|Pyld_Set|为备选的有效载荷集合。

为证明DA4TSC的有效性，在实验中引入经典的贪婪随机自适应搜索(Greedy Randomized Adaptive Search Procedure,GRASP)算法[19]和祝周鹏提出的基于进化计算的卫星平台载荷配置优化算法(Satellite Platform and Payload Selecting Algorithm,SPPSA)[13]作为基线进行比较。由于在问题规模较大的情况下，分支限界、动态规划等精确搜索算法无法在有效时间内给出问题解，所以未将其作为基线比较算法引入实验中。

在GRASP中，首先通过贪婪策略(greedy strategy)构造出满足约束C1的初始解，然后通过局部搜索(local search)方法提升初始解的优化程度，并进行进一步的约束处理，使之满足约束C1～C4。SPPSA按照作者在其论文中所描述的参数数值进行设置。设置DA4TSC种群规模为50，交叉概率为0.90，卫星平台基因位变异概率为0.08，有效载荷基因位变异概率为0.15。初始惩罚系数设置为cp(0)=0.1；惩罚系数上限设置为cmax=10；算法迭代次数上限λmax=50 000；持续不变代数h=200；惩罚系数变化参数θ1=0.96，θ2=0.98。如果连续300代结果没有改进，则算法退出。效费比已经进行了归一化。GRASP中任务接受概率设置为0.5，实验平台为Intel (R) Core i5-9400 CPU + 16G 内存+Windows 10，采用python3.5进行编码实现。

为了降低算法随机性对评价结果的影响，实验中采用3种算法独立计算实验用例50次，然后对计算结果取平均值，实验结果如图4所示。

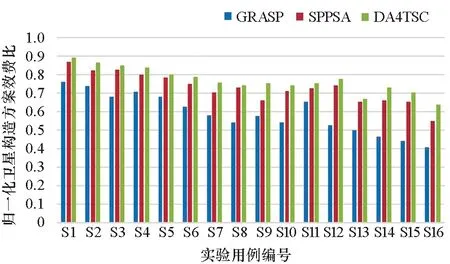
图4 不同算法计算结果比较Fig.4 Comparison of the computation results of different algorithms

由图4可知，相比于GRASP和SPPSA，DA4TSC取得了更好的计算结果。随着问题规模增大(如航天应急任务增多、构造的卫星数量增多、备选卫星平台和有效载荷增多)，DA4TSC的计算优势更加明显。相比于GRASP的贪婪随机搜索策略，两种基于进化计算的算法SPPSA和DA4TSC能够在解空间全局范围内迭代寻优，因而效果均比GRASP好。而与SPPSA相比，DA4TSC具有更加高效的约束处理机制，能够通过对惩罚系数的自适应调整，降低算法陷入局部最优解的概率，从而能够获得更加优化的计算结果。

对基于遗传算法的两种算法SPPSA和DA4TSC的收敛迭代次数进行比较，如图5所示。实验设定为：如果连续300代算法结果不改进，则认为算法收敛而退出；采用两种算法独立计算实验用例50次，然后对收敛迭代次数取平均值。由图5可知，在所有的实验用例中，DA4TSC的迭代次数均低于SPPSA，说明相较于SPPSA，DA4TSC具有更快的收敛速度。这是由于DA4TSC采用了基于自适应罚函数的约束处理机制，罚函数方法能够引导遗传算法从可行解域和不可行解域双向逼近问题最优解，而自适应的惩罚系数调整能够有效地使搜索避免陷入局部最优。因而，DA4TSC面向不同规模、不同分布的问题均能保持较好的收敛性。

图5 元启发式算法收敛迭代次数比较Fig.5 Comparison of the iterative times of nature-inspired metaheuristic algorithms

5 结论

适应任务的模块化卫星快速构建优化决策问题是应急响应空间中出现的新且复杂的问题。本文在深入分析该问题特点的基础上，建立了约束满足问题模型，设计了基于遗传算法的优化决策方法DA4TSC，在约束处理上，引入了基于罚函数法的约束处理方法，针对罚函数法中惩罚系数难于确定的特点，设计了惩罚系数自适应调整的动态罚函数机制。通过实验证明本文所提方法的可用性及有效性。

下一步的工作在于将机器学习方法引入优化决策算法之中。让算法通过对历史优化决策结果的增量式学习能够在计算过程中更加有目的地搜索解空间中更有希望包含最优解的区域，从而进一步提升算法优化性能和收敛速度。