高超声速滑翔再入飞行器的可达区快速预测*

吴 楠，王 锋，赵 敏，孟凡坤

(1.中国人民解放军战略支援部队信息工程大学 数据与目标工程学院，河南 郑州 450001;2.中国人民解放军95894部队，北京 102211)

高超声速滑翔再入飞行器[1-2](Hypersonic Glide Reentry Vehicle,HGRV)的可达区是指在某些约束条件下，飞行器在地球表面上可达范围的边界曲线[3]。可达区作为飞行器纵横向机动能力和打击区域的反映，其计算具有重要意义。

可达区计算的内容包括两个方面，一是最大横程的计算方法，二是边界的获取方式。其中前者的关键是获得倾侧角的变化规律，目前有三种方法：①通过伪谱[4-5]或粒子群[6]等数值优化方法获得倾侧角的变化规律；②利用最优化原理[7]或再入走廊边界[8]推出倾侧角的控制律表达式；③将倾侧角设置为常值[9]。这三种方法的精度、运算量和依赖的先验信息量是逐渐减小的。可达区边界的获取目前有两种方法：①遍历法，即通过计算不同纵程或倾侧角条件下的最大横程弹道，将末段点连接构成边界；②椭圆近似法，即将可达区近似为椭圆形，利用最大纵程和最大横程三个末端点计算椭圆参数形成边界[10]。相比之下遍历法计算的边界与实际更为符合，但带来的问题是运算量急剧增加。

传统的可达区计算方法通常为上述方法的不同组合，在计算精度和运算量上具有较大差异，但均是从飞行器设计方的角度，即在已知详细的参数和约束条件下进行构建，重视准确性而忽略时效性，通常用于飞行器的弹道设计与性能分析。然而对于防御方，对来袭的HGRV进行预警和威胁评估也需要对其可达区进行预测，而传统的可达区计算方法不太适用，原因为：一方面，此时HGRV作为非合作目标，相关参数和约束是未知的；另一方面，可达区计算作为针对HGRV的“预警—探测—预判—拦截”中重要一环，要求需具有准实时性，传统方法具有依赖先验信息偏多、耗时较长的缺陷。

本文在仅已知目标当前时刻的位置、速度和最大升阻比参数(可基于雷达探测数据通过实时弹道估计获得)条件下，对文献[11]中的倾侧角最优控制律进行简化和改进，并引入平衡滑翔和最大升阻比滑翔假设，建立简化的飞行程序控制模型，分别通过一次数值积分获得最大纵程和横程弹道，基于椭圆近似法利用三个末端点构建可达区椭圆边界，以实现对可达区的准实时计算。

1 弹道计算方程的简化

HGRV的三自由度弹道计算方程通常如式(1)所示。

(1)

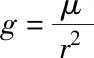
当飞行器飞至中末段或飞行器升阻比有限，而使得剩余飞行时间较短时，可以忽略地球自转，式(1)可简化为

(2)

2 基于最大升阻比平衡滑翔的最大纵程

飞行器最大纵程的计算可以利用三个条件：①倾侧角ν=0，即飞行器在纵向平面运动，不进行横向滚转机动；②平衡滑翔(Equilibrium Glide,EG)假设，弹道平稳便于控制，且过程约束容易满足；③最大升阻比滑翔的近似最优性，与最大纵程优化结果误差小于2%。

平衡滑翔[12]是指飞行器升力与重力达到某种平衡，从而实现平稳滑翔的状态，其优点是利用该假设可显著降低弹道计算的复杂度，提高运算速度，且计算所得的弹道通常满足飞行过程中的动压、热流和过载等约束条件，经常用于再入飞行器滑翔弹道的设计与分析。

平衡滑翔的条件为

(3)

对于最大纵程，ν=0，并综合式(2)和式(3)可得平衡滑翔条件下的升力表达式为

(4)

可以看出，平衡滑翔条件下的升力随着目标的速度、高度和速度倾角变化而变化，但不一定与最大升阻比对应的升力相等，说明平衡滑翔条件可使弹道较为平稳，但射程不一定最大。为获得最大纵程，本文提出一种“最大升阻比平衡滑翔”的虚拟状态，该状态的升力由平衡滑翔条件计算，而气动阻力则由升力和最大升阻比常数表示

(5)

由于Kmax为目标升阻比的极大值，因此Dmin为实际气动阻力的极小值，“最大升阻比平衡滑翔”的本质就是恒定气动阻力极小值条件下的平衡滑翔，从而融合平衡滑翔和最大升阻比滑翔的优势，达到既满足过程约束又近似最大纵程的目的。

将式(5)代入式(2)可得

(6)

将式(4)和式(6)代入式(2)，可得基于最大升阻比平衡滑翔条件下的最大纵程简化计算的积分方程

(7)

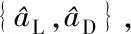
(8)

式中，S和q分别为目标的截面积和动压。

给定某一终端速度约束Vf，便可以利用式(7)通过数值积分算法计算获得最大纵程的终点坐标(λ1,φ1)。

3 基于最优解拟合公式的最大横程计算

基于最优化原理，文献[11]推导出横程的埃格斯公式

(9)

可以看出，横程仅为最大升阻比Kmax和倾侧角ν的函数，如果忽略掉级数项，使横程取得极大值的倾侧角为ν=45°，这也是工程中常用ν=45°的常值倾侧角控制来获得近似最大横程的原因。当最大升阻比较大时，忽略级数项会带来较大误差，实际上最优的倾侧角控制律中，倾侧角是时变的，且与最大升阻比有关。此时最优倾侧角的计算公式可表示为

(10)

式中：βC为横程角，初始为0，随着横程增加而增大；σ-σ0表征速度矢量与飞行纵向平面的夹角，初始为0，逐渐增加至约90°。整体来看，倾侧角随着速度矢量与纵向平面夹角的增加而减小，且在速度矢量与纵向平面垂直前减小至0，防止航程回旋而导致横程减小。而最大升阻比则决定了初始倾侧角的大小，最大升阻比越大，初始倾侧角也越大，说明飞行器用于横向机动的偏转能力越大。

当倾侧角不为0时，将平衡滑翔约束式(3)代入式(2)可得此时的升力表达式

(11)

(12)

仍然基于“最大升阻比平衡滑翔”，可得倾侧角不为0时气动阻力用最大升阻比表示的表达式

(13)

将式(11)和式(13)代入式(2)可得最大横程计算的积分方程

(14)

式(10)和式(14)构成了闭合的最大横程弹道计算方程，方程中仍只有一个未知参数即最大升阻比，采用数值积分算法，即可分别计算左向和右向两条最大横程弹道，弹道终点坐标分别为(λ2,φ2)和(λ3,φ3)。

4 可达区椭圆计算

根据球面几何，已知球面上三点计算球面上的椭圆区域是非常复杂的，考虑到本文研究的飞行器可达区域远小于轨道飞行器的可达区，因此假设飞行器的可达区近似在以落点为中心、经度轴为横轴、纬度轴为纵轴的二维平面区域。

在该经纬度二维平面内，定义可达区为以(λ2,φ2)和(λ3,φ3)间的线段为短轴、(λ1,φ1)到(λ2,φ2)和(λ3,φ3)连线中点的距离为半长轴的半椭圆区域。

椭圆中心的坐标为

(15)

椭圆的长半轴和短半轴为

(16)

该椭圆相当于坐标在原点的标准椭圆先旋转Φ角度，然后再将中心平移至(λ0,φ0)。Φ的计算公式为

(17)

可达区椭圆满足公式

(18)

5 仿真分析

假设地面雷达对某来袭HGRV进行一段稳定跟踪后，通过滤波和实时弹道估计，获得其当前状态参数估计值如表1所示。

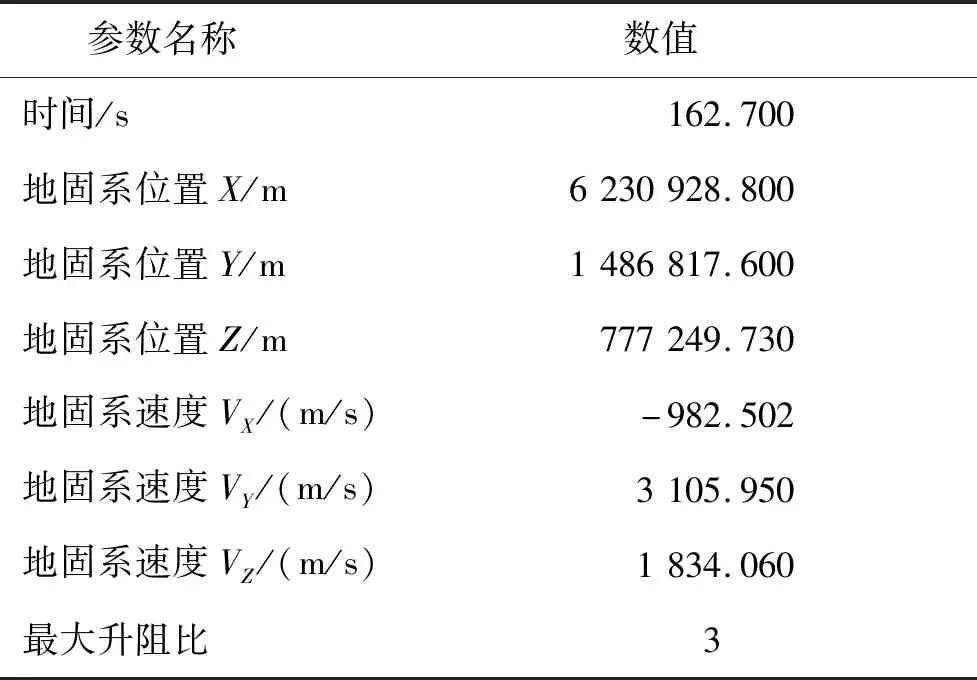
表1 目标当前时刻状态参数估计值Tab.1 State estimation of target at current time

首先将当前状态参数估计转化为本文算法所需的初值，即

[r,φ,λ,V,Θ,σ]=f([X,Y,Z,VX,VY,VZ])

(19)

利用式(7)和式(14)进行数值积分，根据目标打击通常对终端速度的要求，定Vf=1 800 m/s为积分终止条件，便可获得纵程终点坐标和两个横程终点坐标，进而计算可达区椭圆，本文算法计算的HGRV最大纵程、横程以及可达区椭圆结果如表2和图1所示。

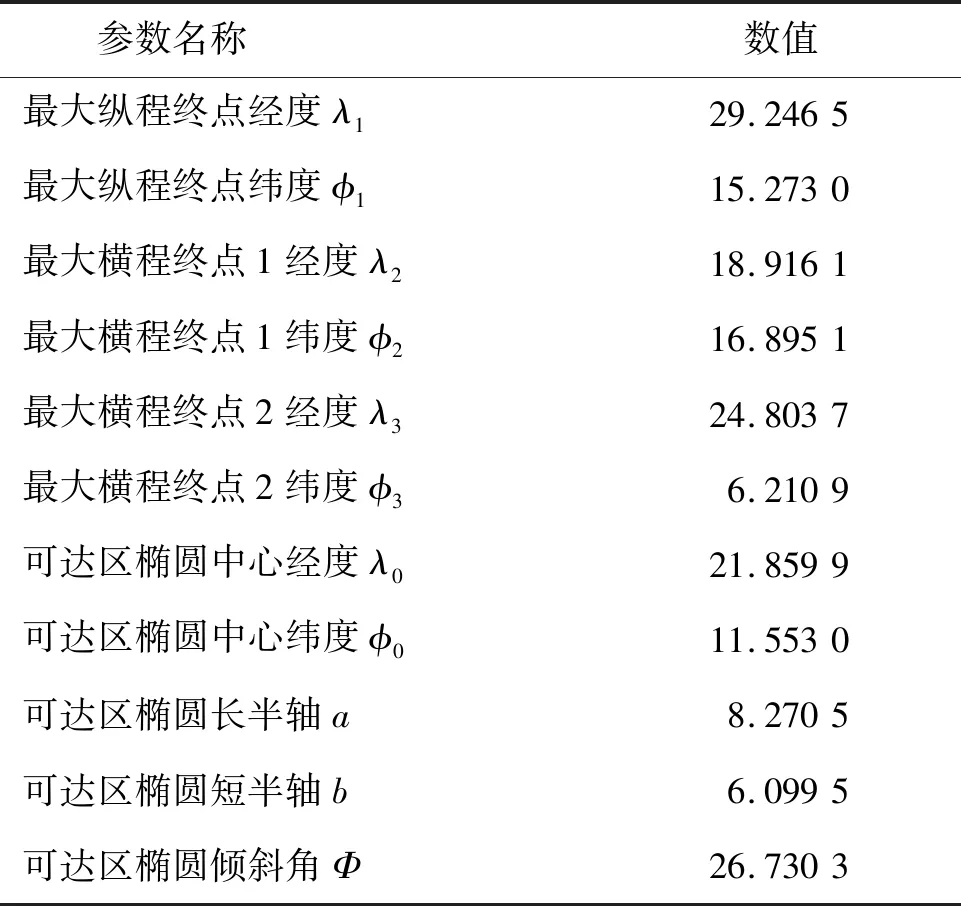
表2 可达区椭圆参数Tab.2 Parameters of footprint ellipse 单位：(°)

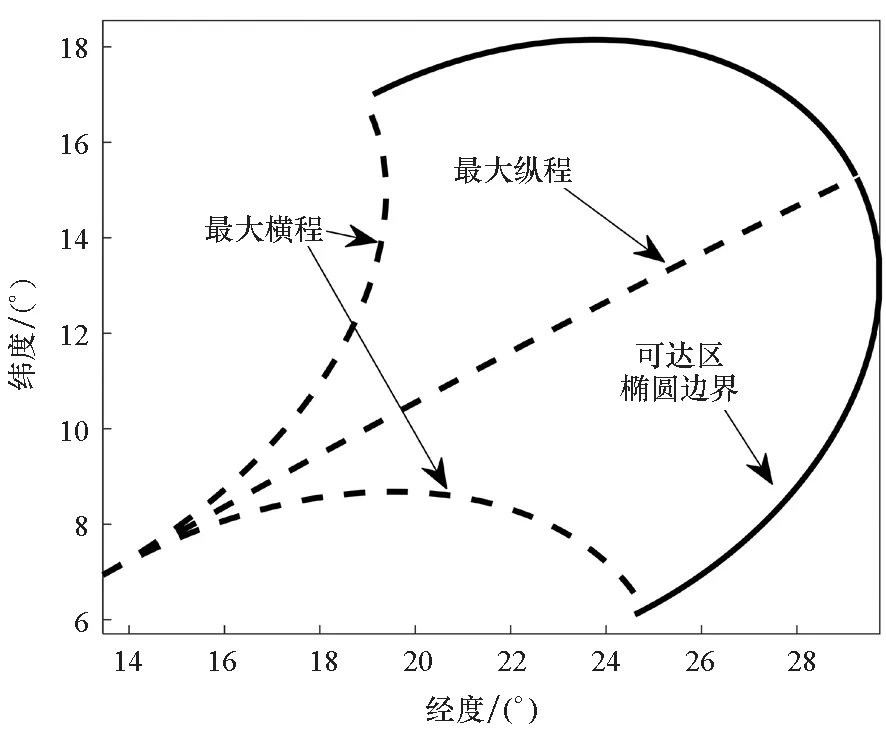
图1 最大纵程和横程地面航迹与可达区椭圆边界Fig.1 Ground track of maximum downrange and crossrange and elliptical boundary of footprint

从结果可以看出，对于本文算例中的HGRV(初始速度约为3 800 m/s，最大升阻比为3)，其最大纵程约1 960 km，最大横程约为650 km，可达区面积(椭圆的前半段)仍可达9×105km2。

为检验本文算法的准确性和有效性，分别采用工程中常用的数值优化方法和常倾侧角方法[14]计算可达区进行比较。其中，数值优化方法计算精度高(但需要利用目标充分的总体参数信息)，可作为结果准确度验证的依据。

数值优化方法参数设置：目标质量、几何和气动参数参考文献[14]，最大动压约束为1.8×105Pa，最大法向过载约束为6，最大驻点热流密度约束为6×105W/m2。攻角最大值为30°，倾侧角最大值为85°，分别计算最大纵程、纵程为最大纵程的0.9、0.8、0.7、0.6、0.5和0.4倍条件下的最大横程共13条优化弹道，对应终点连接构成数值优化方法计算的可达区边界。

常倾侧角方法参数设置：攻角采用给定的标称攻角曲线，分别计算倾侧角为0°、15°、25°、35°、45°、55°和65°的13条弹道，对应终点连接构成常倾侧角方法计算的可达区边界。

将三种方法计算的可达区边界进行比较，如图2所示。

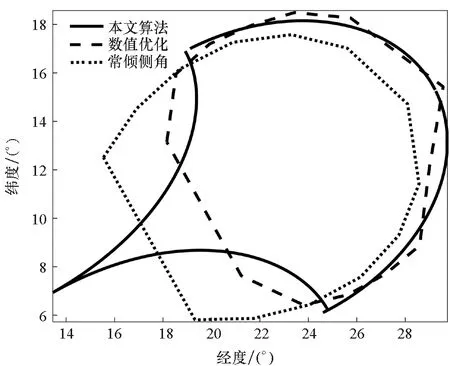
图2 三种方法计算的可达区边界Fig.2 Footprint boundaries by three algorithms

通过比较可以看出，本文算法计算的最大纵程和横程与优化结果相近(最大纵程误差约1.9%，最大横程误差约3%)，可达区边界的椭圆形近似较为合理，可达区椭圆边界几乎与优化的可达区边界重合，由此本文算法的准确性和有效性得到验证。本文算法结果接近了满足过程约束的数值优化结果，这是因为：①最大升阻比滑翔的假设保证其最大射程的近似最优性；②平衡滑翔的假设则保证了所算弹道通常满足过程约束。通过比较本文和数值优化方法计算的最大横程对应的倾侧角变化规律(如图3所示)可以看出，本文构造的倾侧角变化曲线在动压较大的滑翔段基本逼近了数值优化结果，也侧面验证了本文计算结果的近似最优性。

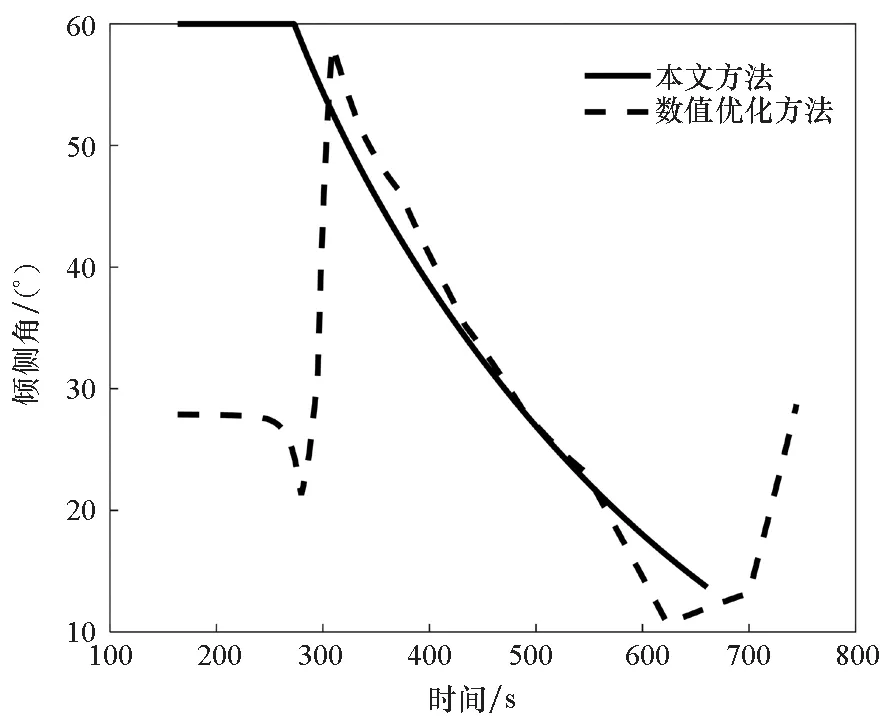
图3 最大横程对应的倾侧角变化曲线Fig.3 Bank angle curves corresponding maximum crossrange

相比之下，常倾侧角方法计算的可达区边界虽在面积和形状上与其他两种结果相近，但存在向初始点方向的整体性偏移，这说明：①常倾侧角45°的控制律确实可以近似获得最大横程，具有较高的工程应用价值；②攻角采用标称曲线，纵程没有优化，导致其射程偏小，造成了可达区边界的整体性前移。

在相同软硬件环境(Core i7 双核处理器，MATLAB2016软件)下，对三种算法耗时进行测量，结果为：数值优化方法约231 s，常倾侧角方法约1.04 s，本文算法0.24 s。可以看出，数值优化方法耗时最长，且依赖目标的先验信息量较大，不太适用于防御方的目标实时预警；常倾侧角方法和本文方法由于不需要优化迭代，耗时较短，但由于常倾侧角方法计算弹道条数较多，因此其耗时略大于本文方法。

本文算法依赖较少的目标先验信息，且具有较高的运算精度和速度，可对HGRV类目标进行准实时连续的可达区预测，适用于防御方针对HGRV类目标的实时预警。随着HGRV飞行速度的逐渐减小，所计算的可达区椭圆边界精度会逐渐提高，可达区面积逐渐收缩，为目标威胁评估和防御决策提供的信息也更为准确。另外，可达区椭圆边界计算的准确程度也强依赖于前期对HGRV状态参数和气动参数估计的准确程度。

6 结论

本文基于平衡滑翔和最优化飞行准则，在获得有限的HGRV弹道估计参数(基于雷达探测数据通过实时弹道估计获得目标当前时刻的位置、速度和最大升阻比参数)条件下，提出了一种适用于防御方进行HGRV类目标预警的可达区边界快速计算方法。仿真结果表明，与传统方法相比，本文方法具有利用先验信息少、精度较高和运算量小的优点，可以满足实时性需求，可为针对HGRV类目标的威胁判断和防御决策提供有效的数据支持。