采用威布尔分布的道岔梁的寿命预测及评估

杜子学， 王奥

(重庆交通大学 机电与车辆工程学院， 重庆 400074)

随着都市化进程的发展，交通运营面临着空前的压力.目前，城市交通除了地面上的公共汽车、私家车等，在一些城市中还引入了轨道交通，如轻轨、有轨电车、无轨电车等.新兴的轨道交通大致可分为地铁、有轨电车、轻轨、市郊快速铁道、城际铁道、磁悬浮等.跨座式单轨列车作为典型的轨道交通，在日本和中国重庆被广泛应用.重庆轻轨三号线因占地小、工期短、成本低、景观性特别而闻名.

跨座式单轨道岔梁按照结构形式可以分为关节型道岔梁和关节可挠型道岔梁[1].车辆行驶在道岔梁上，梁上表面与走行轮相连接，负责承载垂向载荷，两侧则与导向轮连接.目前，国内学者多对各种道岔梁进行力学和动力学分析.尤加杰[2]对轨道梁进行稳定性分析；薛小强[3]对轨道梁进行瞬时动力学分析；牛均宽[4]对跨座式关节型道岔梁进行有限元静力学初步分析，通过试验验证有限元分析的正确性；李振华[5]对跨座式单轨平移式道岔梁进行静、动力学分析；陈源等[6]对跨座式单轨道岔电气系统进行方案设计；王智祥等[7]对跨座式关节型道岔梁进行静、动力学及疲劳寿命分析.本文采用Femfat软件对道岔梁的焊缝结构进行建模和寿命预测，从而验证焊缝寿命能否满足实际工况的运营需求.

1 道岔梁的有限元建模

有限元(FEM)软件中,考虑合适的网格类型和尺寸对道岔梁进行网格划分.道岔梁以板件为主，故大多以面网格四边形壳单元为主，为满足网格质量，实体单元可先进行面网格划分,再拉伸为实体网格.网格尺寸太大会使计算结果粗糙，网格尺寸太小则会对计算机的运算性能提出更高的要求，增加运行时间.综上，网格大小取10 mm为宜，FEM模型离散为1 164 825个单元，1 169 095个节点[8].道岔梁FEM模型,如图1所示.

图1 道岔梁FEM模型Fig.1 FEM model of turnout beam

进行网格划分后，在考虑网格翘曲角、长宽比、雅可比、偏斜度、三角形单元最大最小内角和四边形单元最大最小内角条件下，对网格质量进行检查.道岔梁材料为Q235，其力学特性如下：弹性模量为209 GPa；泊松比为0.3；密度为7.9×103kg·cm-3；抗拉强度为490 MPa；屈服强度为235 MPa.

2 道岔梁的模态分析

2.1 自由模态

跨座式单轨道岔梁为简支梁结构，将道岔梁进行有限元网格划分后，还需要进行模态分析.这是因为在设计初始阶段对道岔梁进行固有动态特性的分析和计算，可以得到每一阶模态的固有频率和振型，从而有效避免道岔梁的设计缺陷，让道岔梁的动力学特性更加合理，在规避车轨耦合的共振的同时，又能提高乘坐的舒适性.

定义分析道岔梁的12阶自由模态，因为前6阶自由模态均为刚体位移，频率值近乎为零，故不作考虑.道岔梁的自由模态分析结果,如表1所示.表1中：f为频率.

表1 道岔梁的自由模态分析结果Tab.1 Free modal analysis results of turnout beam

道岔梁的第11，12阶自由模态振型图,如图2,3所示.

图2 道岔梁的第11阶自由模态振型图 图3 道岔梁的第12阶自由模态振型图Fig.2 11th free mode diagram of turnout beam Fig.3 12th free mode diagram of turnout beam

2.2 约束模态

与自由模态相比，由于道岔梁为简支梁结构，约束模态按照实际工况约束两端，并限制x,y,z的转动和移动自由度.单轨车的行驶频率为6～10 Hz,而约束模态频率值均高于自由模态，能够避免车轨接触时发生的耦合效应.道岔梁的第5，6阶约束模态振型图，如图4,5所示.

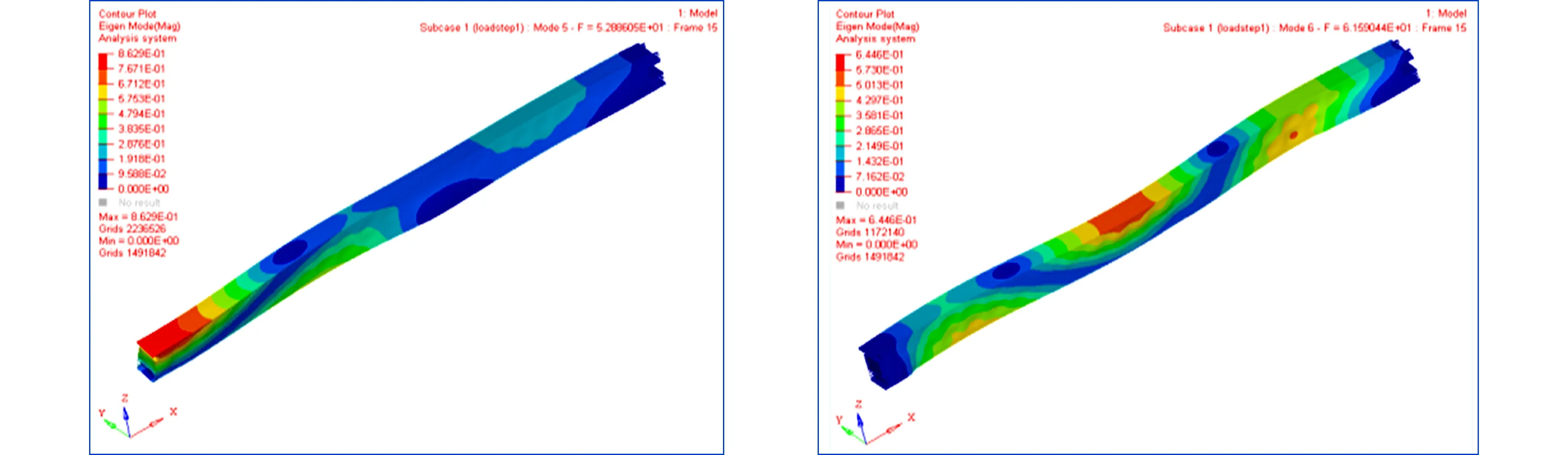
图4 道岔梁的第5阶约束模态振型图 图5 道岔梁的第6阶约束模态振型图 Fig.4 5th constrained mode diagram of turnout beam Fig.5 6th constrained mode diagram of turnout beam

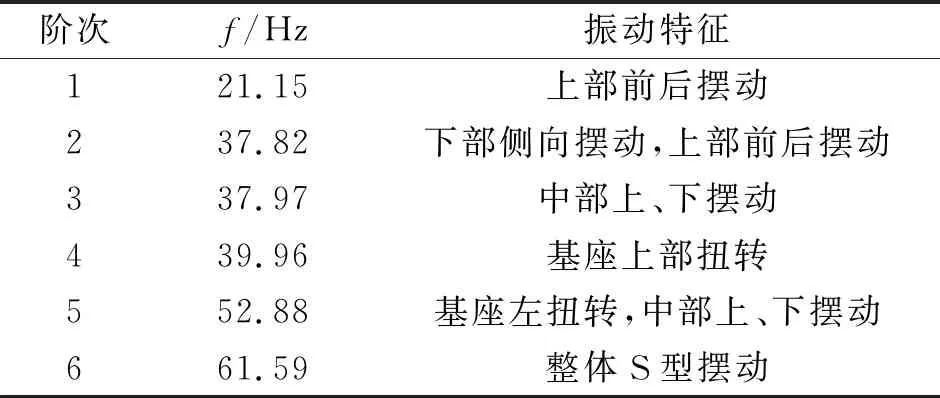
表2 道岔梁的前6阶约束模态分析结果Tab.2 Analysis results of first 6 constrained modes of turnout beam

道岔梁的前6阶约束模态分析结果，如表2所示.由表2可知:在约束状态下，道岔梁前6阶频率为21.15～61.59 Hz,可以避开列车频率(列车在行驶过道岔梁时的激振频率为4.34～12.74 Hz)，有效地避免了与道岔梁的共振现象[9-10].

3 载荷-时间历程

在有限元疲劳分析方法中，载荷谱直接决定了疲劳分析结果的准确性.目前，载荷谱的提取方法大致有两种：一种是用实测贴应变片的方法，但是该法要搭建实验场地，受到时间成本和经济成本的限制；另一种是采用多刚体动力学仿真的方法，在动力学软件中建立准确的转向架运动模型、约束、力元等，设置仿真时间，通过轮轨耦合提取载荷谱.

在多体动力学软件中，选取A级路面作为随机路面，设定车速为50 km·h-1满载行驶.由于走形轮轮胎面与道岔梁相接触，故选取走形轮处的载荷-时间历程作为激励，得到的满载工况50 km·h-1下的载荷(F)-时间(t)历程，如图6所示.

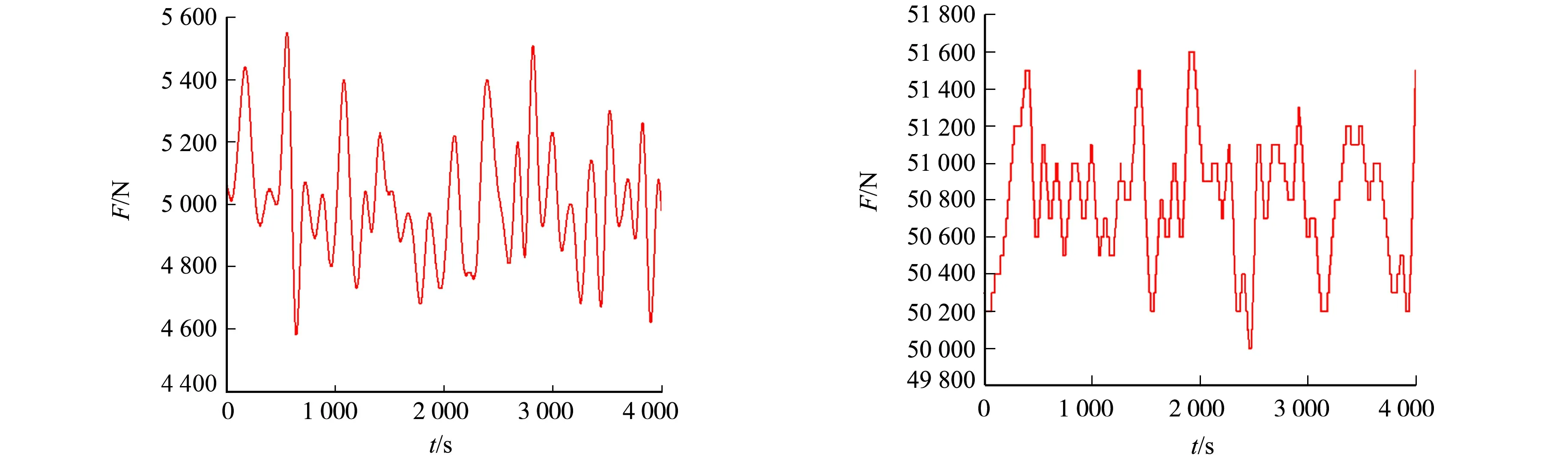
(a) 前左、前右走形轮直线工况 (b) 后左、后右走形轮直线工况图6 满载工况50 km·h-1下的载荷-时间历程Fig.6 Load-time history at 50 km·h-1 under full load condition

4 道岔梁的焊缝疲劳分析

准静态应力法是一种在受到外载荷历程下线弹性结构应力的分析方法，这种方法主要是计算在特定载荷工况下，任一时刻的相同结构位置和相同方向作用的单位静载荷引起的弹性应力-应变状态；然后，叠加对应的实测或动力学仿真获得的载荷谱.同理，分别进行单位载荷作用下的应力分析，选取单轨车辆在道岔梁上行驶的两种典型工况进行分析，通过载荷-时间历程和单位载荷产生的静态应力影响因子(stress influence coeffcient,SIC)相乘叠加原则，计算结构上应力历程[11].

某节点准静态应力计算式为

(1)

式(1)中：σx,i,σy,i为应力影响系数;Fi(t)为载荷-时间历程，其中,结构部件同位置、同方向与载荷-时间历程相当的单位载荷决定了应力影响系数；σx,σy,τxy分别为载荷作用下的三向应力.

单位载荷下道岔梁的应力图，如图7所示.根据实际工况，施加位置为走形轮与道岔梁接触部分.

(a) 前左走形轮 (b) 前右走形轮

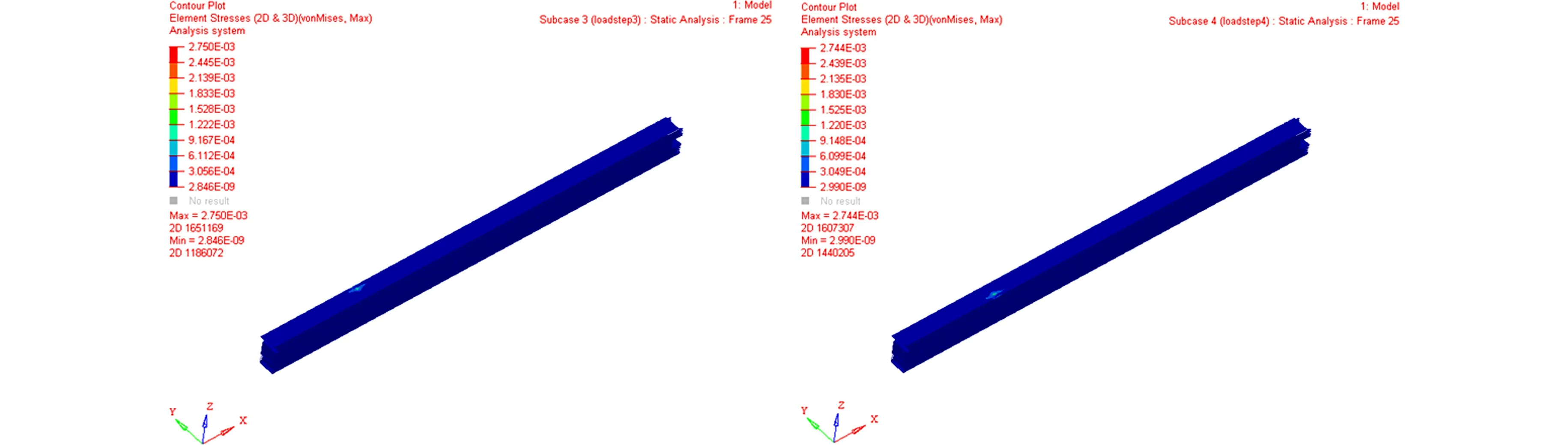
(c) 后左走形轮 (d) 后右走形轮图7 单位载荷下道岔梁的应力图Fig.7 Stress diagram of turnout beam under unit load

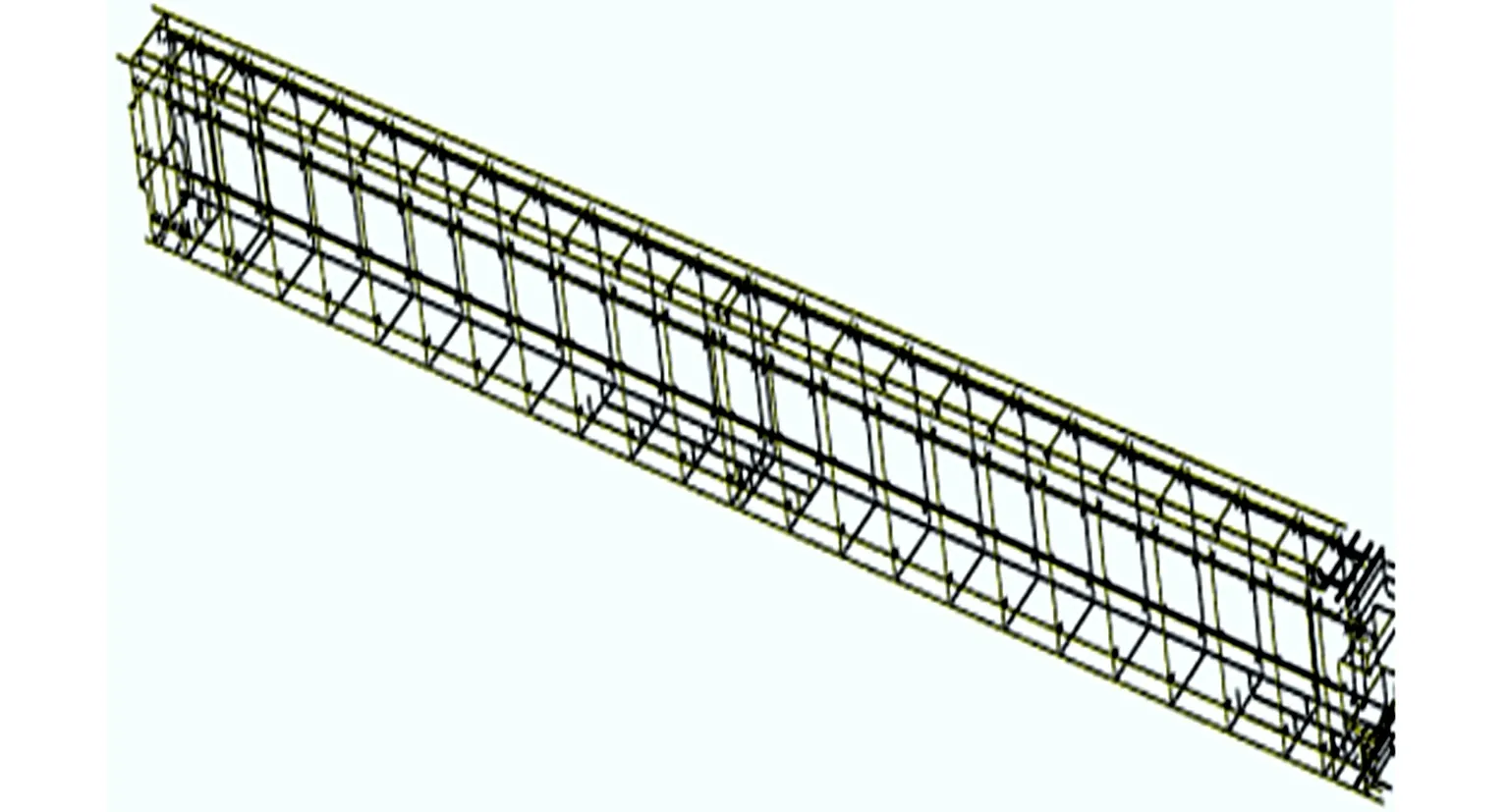
图8 疲劳软件中焊缝的定义图Fig.8 Definition diagram of weld in fatigue software

5 道岔梁的焊缝疲劳寿命流程模型

5.1 道岔梁焊缝的定义

将道岔梁在有限元软件中进行有限元网格划分后，导入疲劳分析软件进行焊缝接头的定义.道岔梁的服役破坏主要分两种形式：静载荷作用下的静强度破坏和来自车体运行动载荷作用产生的疲劳破坏.道岔梁的焊缝由于其特殊的工艺性，对焊缝焊接接头的强度提出了更高的要求.

疲劳软件中焊缝的定义图，如图8所示.在疲劳分析软件中,共定义了720条焊缝，焊缝类型多选择T型焊及十字焊，少部分选用平焊等.

5.2 分析流程及具体参数设置

将单位载荷的应力文件导入Femfat软件中，用软件自带的应力修正方法进行修正.设置存活率为90%，在多通道分析模块中导入载荷-时间历程，使载荷历程与加载荷步一一对应.新建焊缝材料为Q235.用软件自带的应力修正方法进行修正，分析流程如图9所示.

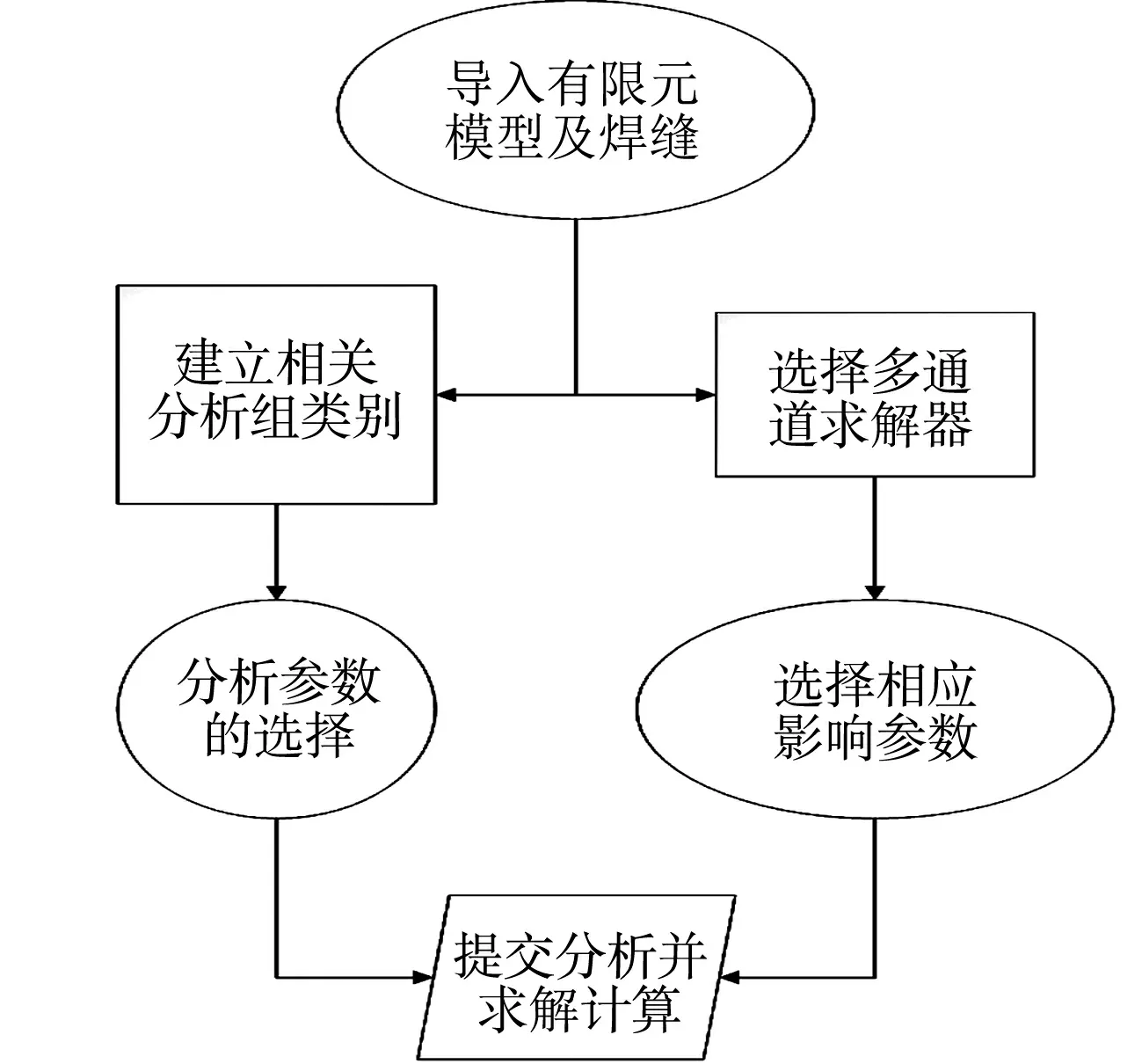
图9 Femfat疲劳软件分析流程Fig.9 Analysis flow of Femfat fatigue software

6 道岔梁焊缝寿命预测

将材料属性、载荷谱文件定义于Femfat疲劳软件中，对节点组赋予各种参数(表面处理、温度场、离散度、微观结构参数、表面粗糙度等).定义缺口应力集中系数，考虑应力梯度和平均应力的影响.

基于线性累计损伤学说，焊缝定义后，对焊缝进行寿命评估预测.考虑极限工况及满载工况下，得到时速50 km·h-1时焊缝疲劳的损伤分布云图，如图10所示.

采用偏保守的Goodman平均应力修正法，即

(2)

式(2)中：Sa为应力幅;SN为修正之后的等效应力幅；Sm为平均应力;Su为极限拉伸强度(UTS).

在疲劳软件中，对相应的参数进行设定和修正，设置相应位置的通道，关联单位应力工况下的应力文件与对应的载荷时间历程,得到疲劳分析流程.基于Palmgren-Miner线性累积损伤理论，对道岔梁的焊缝进行疲劳寿命分析，结果如图11所示.

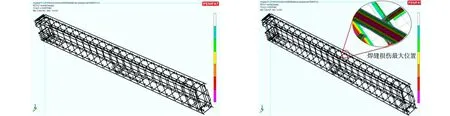
图10 焊缝疲劳的损伤分布云图 图11 焊缝疲劳寿命分析结果 Fig.10 Damage distribution nephogram of weld fatigue Fig.11 Fatigue life analysis results of weld

由图10可知：焊缝疲劳寿命最短位置位于道岔梁中部，道岔面与走形轮接触部位可经受的循环次数为3.24×107[12].

道岔焊缝的疲劳寿命按照极限工况下考虑，即列车每节车厢有2个转向架，每列按8节车厢计算，依据高峰运营情况每1.5 min发车一次，列车每天工作16 h，全年工作天数为365 d.工作年限计算式为工作年限=循环次数×(发车间隙+通过时间/60)/365×16×60，代入相应数据得3.24×107×(1.5+12.2/60)/365×16×60=92.46 a.该结果完全满足道岔梁对焊缝寿命的要求.

7 威布尔分布的构架寿命评估

7.1 威布尔分布数学模型的建立

在结构疲劳分析的设计中，对疲劳强度的描述可分为正态分布函数和威布尔分布函数[13].

威布尔分布的概率密度函数F(ts)为

(3)

式(3)中：ts为试件寿命；ta为威布尔分布的特征寿命；t0为破坏概率为零的试件寿命(最小寿命)；b为形状参数.

在工作应力的统计中，常需要将式(3)进行一定的改写，故障密度函数f(ts)表达式为

(4)

累积故障分布函数表达式为

(5)

式(4)，(5)中：β为形状参数；η为尺度参数.当t0=0时，三参数威布尔分布变为二参数分布，即

(6)

(7)

7.2 威布尔分布函数双参数的确定

双参数威布尔分布中的形状参数和尺度参数的确立方式主要有威布尔概率纸法和Excel拟合计算方法.由于概率纸法需要手工描点作图，工作量繁琐，故采用Excel拟合计算方法.

由于道岔梁近似为两端约束、中部悬空的简支梁，故在承受垂向载荷时，道岔梁中部所受弯矩最大，最易发生疲劳断裂.因此，选取梁中部的20个点作为重点关注点，并按照关注点寿命大小进行排序，计算各关注点的中位秩r，即r=(j-0.3)/(n+0.4).其中：j为节点排序数，j=1,2,…,20；n为危险节点数，此处取20.

求出每个危险节点的中位秩，代入故障概率表中,结果如表3所示.表3中：N为循环次数；r表示F(t)的中位秩.将表3中lnN与ln{ln[1/(1-r)]}分别作为横坐标与纵坐标，采用Excel对其进行一次线性拟合，结果如图12所示.根据图12得到的拟合关系式为y=0.264 9x-7.255 8，其对应的形状参数β=0.264 9，尺寸参数η=-7.255 8.

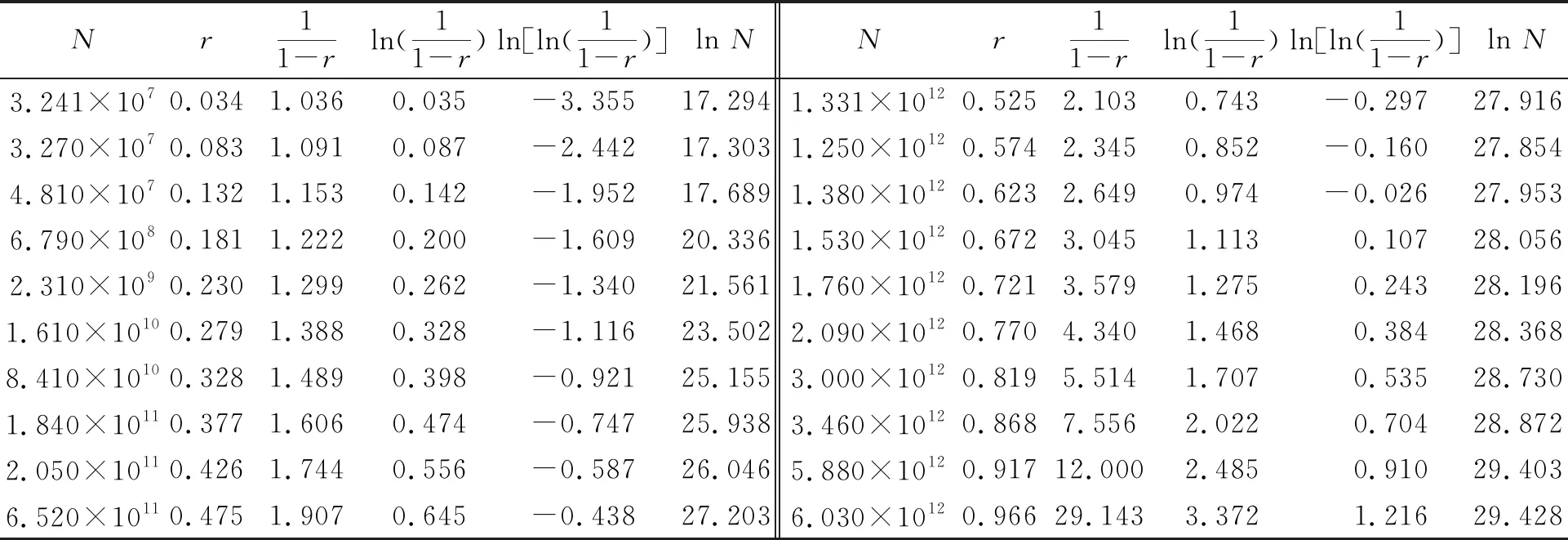
表3 故障概率表Tab.3 Failure probabilityTable

图13为浴盆曲线.由图13可知：当形状参数β<1时，处于浴盆曲线夭折早期.因此，关注节点故障率随着时间的增加而减少.

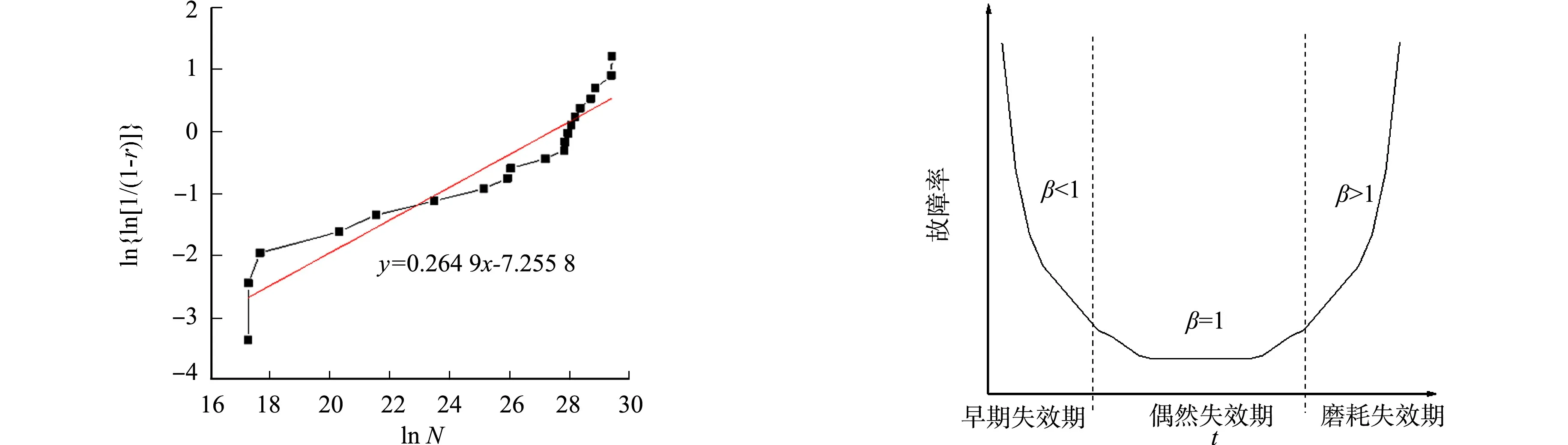
图12 线性拟合图 图13 浴盆曲线 Fig.12 Linear fit graph Fig.13 Bathtub curve

8 结论

借助有限元方法对跨座式单轨道岔梁进行网格划分离散化，用壳单元和实体单元对其进行模拟，保证其较高的单元质量，能够得到较高的后处理精确度.

1) 在疲劳软件中,对焊缝进行建模和定义，选择准确的焊缝类型及其接头类型.结果显示：在极限工况下，道岔的焊缝寿命能够满足实际运营工况的需求.

2) 焊缝强度较弱部分容易出现疲劳断裂，可以选择焊接外形修正的方法，如对部件相应位置进行机械表面加工、电弧整形及特殊的焊接工艺处理，或采用调整残余应力的方法，如应力释放、超载预拉伸、局部整形等[14].

3) 将威布尔分布评估方法[15-17]应用到有限元的危险节点评估中，为焊缝的疲劳强度预测提供了新的方案.