二阶时滞多智能体系统分组一致性分析

李艳艳， 李钟慎

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

多智能体系统一致性在电力、交通、多机器人协同控制等方面得到广泛的应用[1-4].多智能体系统一致性指的是随着时间的推移，智能体之间进行信息交换，最后，使得各智能体的状态达到相同的值.一致性协议是智能体之间进行信息交换后状态达到一致的规则.多智能体系统一致性问题作为多智能系统研究的基本问题之一，许多学者在这一问题上得到了丰富的理论成果.这些成果包括一阶时滞多智能体系统一致性的研究[5]、具有动态拓扑和不同时延的二阶多智能体系统的一致性的分析[6]、具有时滞的多智能体系统一致性控制协议的设计[7]及基于二阶网络的时滞多智能体一致性控制协议的设计[8]等.朱雪芳等[5]研究基于加权平均预测的一阶时滞多智能体系统的一致性问题，提高系统的鲁棒性和收敛速度.闫超等[6]设计一种新邻居的反馈法则，研究在动态拓扑下具有不同通信时滞的二阶多智能体系统.林淼[7]设计具有时滞的二阶和三阶多智能体系统分布式协同控制策略和提高系统收敛速度的局部控制策略.戴彬婷等[8]提出带有延时基于二阶网络的多智能体一致性控制和跟踪算法，并且在提升系统一致性收敛速度基础上研究编队控制算法.

近年来，分组一致性问题成为多智能体系统的研究热点之一.对多个智能体系统进行分组，使得子系统中各智能体的状态达到一定的值，不同子系统达到的状态不一样.Yu等[9]提出通信拓扑之间的交换存在通信延迟，引入双树行变换对原系统进行降阶，在加权有向图下，对一阶系统分组一致性的时滞和切换情况进行研究，并设计一阶系统分组一致性若干法则.Xie等[10]提出连续时间多智能体系统的分组一致性充分必要准则.Xia等[11]提出在切换拓扑和时变时滞情况下，一阶多智能体分组一致性的充分条件.Han等[12]提出智能度的概念，利用多一致性的方法，给出二阶系统在采样控制下实现分组一致性的充分必要条件.

在实际应用中，相互联系的多智能体之间不仅存在合作关系，也存在竞争关系.然而，基于竞争关系的多智能体研究问题却少有报道.文献[13-19]基于竞争协议下，研究一阶多智能体无时滞和时滞情况下的分组一致性问题.林瑜阳等[14]研究二阶多智能体基于竞争协议下的分组一致性问题.本文在文献[14]的基础上，将无时滞的多智能体系统拓展到有时滞的多智能系统，给出二阶时滞多智能体系统分组一致性的竞争协议，并给出系统实现分组一致性所容许的最大时滞及实现分组一致性的充分必要条件.

1 预备知识与问题描述

1.1 代数图论

设G={V,E}表示一个无向图，V={v1,v2,v3,…,vn}表示顶点的集合， 即多智能体系统的集合.E⊂V×V表示图的边集，即智能体之间信息交换.(vi，vj)∈E表示顶点vi能够接收到顶点vj传递的信息，顶点vi的邻居集合用N表示.其中，Ni={vj∈V}.图G的邻接矩阵A=ai,j⊂Rn×n，ai,j表示vi和vj之间的连接权值.当vj∈Ni时，ai,j>0;否则,ai,j=0.

对于无向图ai,j=aj,i.文中不考虑自环拓扑结构度矩阵D=[di，j]n×n，di，j表达式为

(1)

式(1)中：k为1,2,3，…,n.存在无向序列{(vi,1,vi,2)，(vi,2,vi,3)，…,(vi,r,vj)}使vi到达vj，则称vi和vj是连通的.若无向图中任意两点是连通的，则称该图是无向连通图.

1.2 问题描述

以连续二阶多智能体系统为研究对象，每个智能体系统的动态模型描述为

(2)

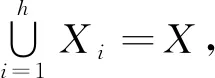
定义2分组一致性.给定系统初始条件x(0)=[x1(0),x2(0),x3(0),…,xn(0)]T，v(0)=[v1(0),

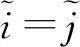
研究带有通信时滞的二阶多智能体系统，设计基于竞争的控制协议的控制输入为

(3)

式(3)中:γ>0表示耦合系数;τ为系统时滞.由式(2)，多智能系统的方程为

(4)

其对应的矩阵形式为

(5)

式(5)中：x=[x1,x2,x3,…,xn]T;v=[v1,v2,v3,…,vn]T;L=D+A.

2 主要结果及其证明

为了研究系统(3)在时滞情况下的分组一致性问题，给出引理1,2.

引理1如果图G(t)的拓扑结构为连通二部图，则在适当排序下，图G对应的邻接矩阵A为

引理2如果图G的拓扑结构为连通二部图，则矩阵D+A的秩为n-1，矩阵D+A的非零特征值为正实数.

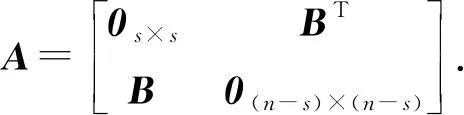
定理1设二阶时滞多智能体的拓扑结构为连通二部图，当γ>0时，利用控制协议(3),系统(4),可以达到分组一致，0<τ<τ*即为系统的最大时滞.

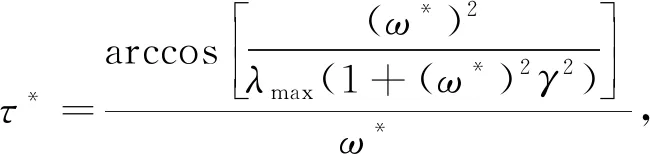
(6)

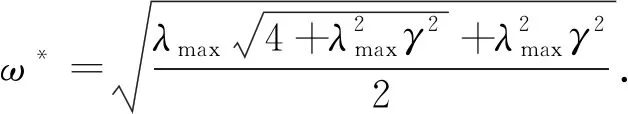
(7)

证明:利用频域分析法对系统(4)的稳定性进行分析，并求出系统进行分组一致时τ的取值范围.对系统(4)进行拉普拉斯变换,即

Χ(s)=G(s)x(0).

(8)

令Y(s)=sIn-In⊗S-L⊗Re-τ,s，由定理2，存在可逆矩阵F，使得J=F-1LF=diag{0,λ2,…,λn}，其中，0=λ1<λ2<…≤λn为正实数且为(D+A)的特征值.

Y(s)=(F⊗I2)(FT⊗I2)Y(s)(F⊗I2)(FT⊗I2)=(F⊗I2)[sIn-In⊗S-L⊗Re-τs)(FT⊗I2)-

(9)

由式(9),有

(10)

由式(10)可知，Y(s)除了两个零特征值，其余零点均位于左半开平面，当且仅当

s2+sλiγe-τ,s+λie-τ,s=0

(11)

的根全部位于左半平面.将s=jω带入式(11)，λi为正实数,有

-ω2+ωγλisin(τω)+λicos(τω)=0，

(12)

ωγλicos(τ)-λisin(τω)=0.

(13)

由式(12)，(13)，可得

(14)

因此，最小时滞τ为

(15)

当ω>0时，ω随λi的增大而增大，而arccosx是一个减函数，所以τ是关于λi的减函数，记λmax=maxλi为系统能容许的最大时滞，有

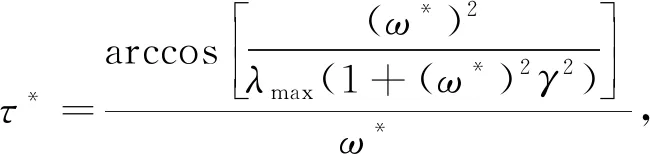
(16)

(17)

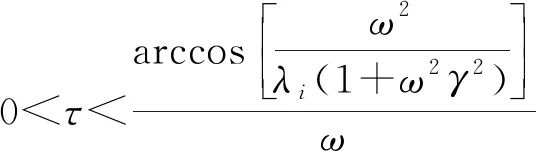
(18)

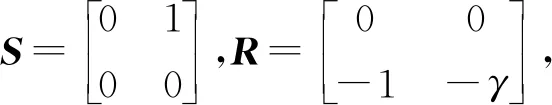
(19)

由文献[10]，由于式(17)除两个零特征值外，其余特征值均分布在坐标轴的左半平面，所以系统收敛，可实现分组一致.

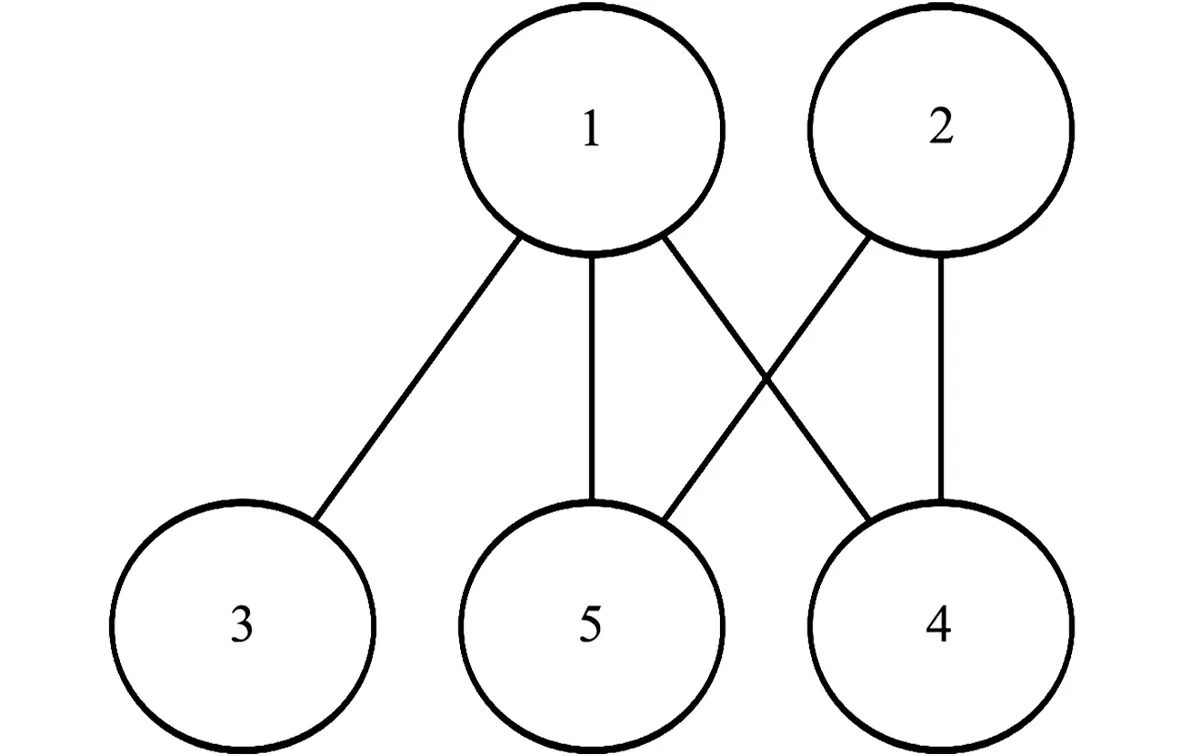
图1 5个多智能体系统的 连通二部图Fig.1 Connected binomial graph with 5 multi-agent systems

3 数值仿真

图1为5个多智能体的连通二部图.图1中：两顶点间连接权重为1；任意产生的初始状态为x(0)=[-6,5,-6,0,6]T， 而v(0)=[4,7,-5,3,2]T.取耦合系数γ=1，τ*=0.29，有0<τ<0.29.

当γ=1时，τ=0.134时，即当多智能体系统时滞在最大容许时滞范围内，系统的各状态响应，如图2所示.图2中：x为位置；v为速度.由图2可知：智能体系统1,2收敛于同一位置和速度，而智能体系统3～5收敛于同一位置和速度，多智能体系统实现分组一致性.

当γ=1时，τ=0.290时，即当多智能体系统时滞处于最大容许时滞时，系统的各状态响应，如图3所示.由图3可知：智能体系统1,2收敛于同一位置和速度，智能体系统3～5收敛于同一位置和速度，并且多智能系统出现振荡，仍然能够实现分组一致,但处于临界稳定的状态.

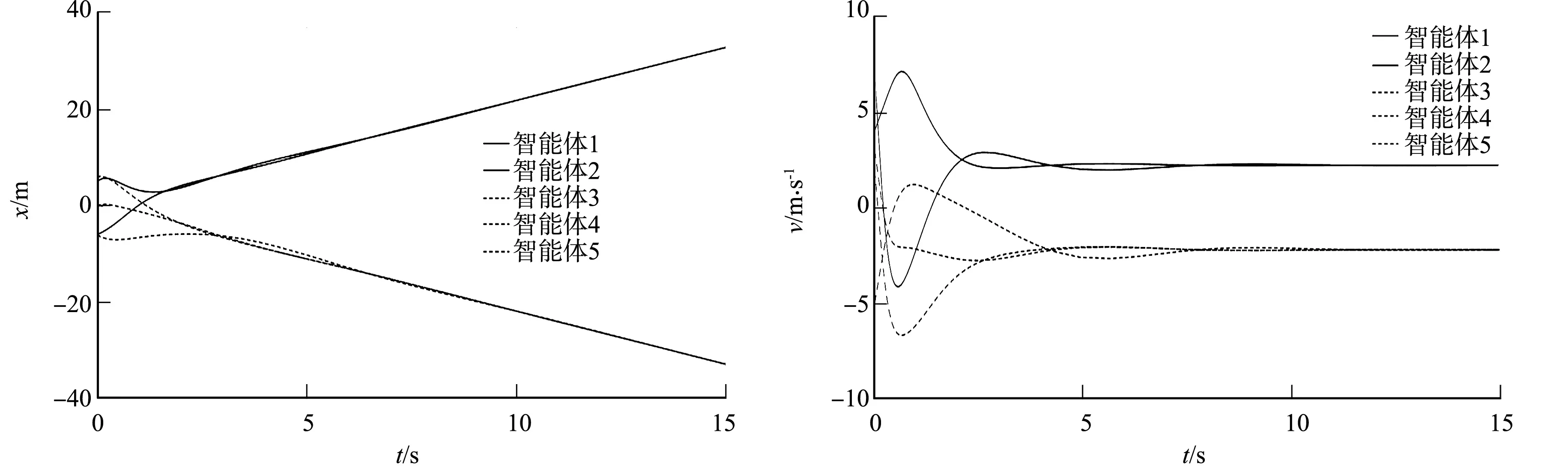
(a) 位置响应 (b) 速度响应图2 系统的各状态响应(γ=1，τ=0.134)Fig.2 Every state response of system (γ=1， τ=0.134)

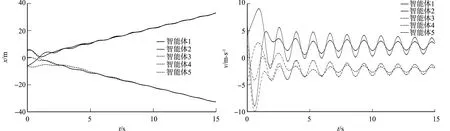
(a) 位置响应 (b) 速度响应图3 系统的各状态响应(γ=1，τ=0.290)Fig.3 Every state response of system (γ=1， τ=0.290)

当γ=1时，τ=0.350时，即多智能体系统时滞超过最大容许时滞，系统的各状态响应，如图4所示.由图4可知：智能体系统1,2既不收敛于同一位置和速度，智能体系统3～5也不收敛于同一位置和速度，即各智能体系统的状态发散，验证了定理1的正确性.

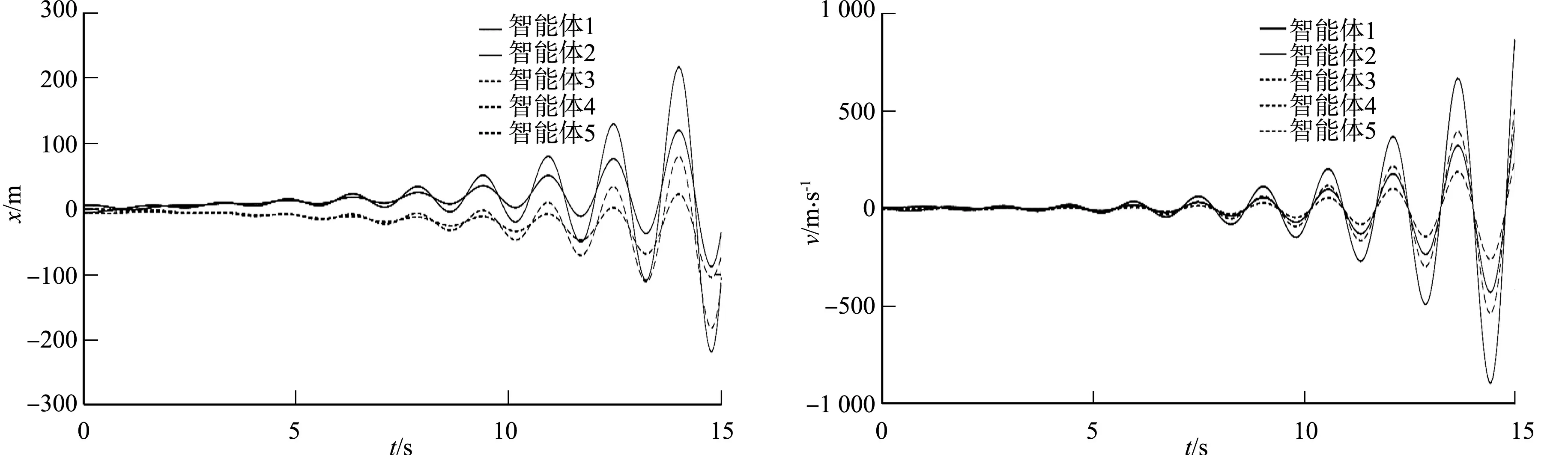
(a) 位置响应 (b) 速度响应图4 系统的各状态响应(γ=1，τ=0.350)Fig.4 Every state response of system (γ=1， τ=0.350)

4 结论

研究二阶时滞多智能体系统在连通二部图下分组一致性问题，根据连通二部图的特征，设计基于竞争的二阶时滞多智能体系统的分组一致性协议，通过频域分析法得到系统分组一致性的充要条件，通过数值仿真验证了结果的正确性.

文中仅研究了连续二阶时滞多智能体系统的在连通二部图下的分组一致性问题，对于基于连通二部图下的离散多智能体系统、非线性多智能体系统的分组一致问题是后续将要解决的问题.