考虑风电不确定性的自适应MPC负荷频率控制方法

2021-02-01赵熙临马艺菡付波程鑫罗润玉

华侨大学学报（自然科学版） 2021年1期

赵熙临，马艺菡，付波，程鑫，罗润玉

(湖北工业大学电气与电子工程学院，湖北武汉 430068)

近年来,电力发展与环境保护的矛盾性使清洁能源的应用与研究发展迅速，也使电网中风电渗透率不断提高.由于风能的不确定性，高渗透率风电并网会对电力系统的安全稳定运行带来负面影响[1].这种负面影响体现在：一方面，由于风速的不确定性，使风电机组的有效发电量发生改变；另一方面，随着风电渗透率的提高，电力系统相对转动惯量降低.这些都对电力系统自动发电控制(AGC)提出了更高的要求[2].

为了解决这些问题，学者们开始聚焦于风电参与AGC方法的研究.文献[3-4]研究了风电参与调频对AGC系统参数的影响，结果表明，含风电的电网动态频率特性与电力系统的总惯性时间常数H密切相关.因此，明确风电不确定性与H的对应关系及其对传统负荷频率控制的影响至关重要.文献[5-6]提出风电机组等效虚拟惯性时间常数的变化可以表示为风速、转子转速或机组出力的函数，变参数虚拟惯性控制会影响机组的有效储能，且风机虚拟惯性时间常数He的变化会改变电力系统的总惯性时间常数H，从而改变系统模型参数.针对上述问题，田新首等[6]提出一种变参数有功功率补偿策略，通过判断频率偏差变化范围调整该策略中有功功率参数，但该补偿策略并未直接体现不确定性变化时系统模型的变化.Gloe等[7]针对阵风和低风速时风力发电机存在的变参数综合惯性的问题,提出将惯性常数与转速成比例调节，设计一种变量H控制器，从而提高惯性较小的电力系统的稳定性.但是当不确定性风电对含风电的AGC系统参数产生影响时，对控制器进行动态控制调整是解决问题的关键.

当风电参与AGC进行系统调频时，主要涉及惯性和桨矩角控制.一般而言，在转子惯性控制中，对风机增加频率辅助控制回路，以释放转子中存储的动能，短时间补偿电力系统有功的缺失，支撑频率的调整[8].然而，传统的惯性控制受到转速恢复模块的影响，导致提取的动能减少，并且容易造成频率的二次跌落[9].同时，为了使风机获得稳定的一次调频能力，有学者通过桨距角的调节方式来实现.Zhang等[10]通过设置初始减载率，使风机运行于减载状态，在风机运行过程中根据频率的偏差，动态地调节桨距角以改变风机的有功输出，从而参与电力系统的频率调整.但是基于桨距角控制的频率调整方法响应速度较慢，不能很好地适应电网频率的快速调整需求[9,11].这些问题导致风机参与AGC系统的控制带来的功率补偿是有限的，同时，由于风电的参与使AGC系统的参数发生变化，都对控制器的设计提出了更高的要求.当系统参数在系统运行过程中发生变化时，控制方法的设计至关重要.目前，比例积分微分(PID)控制器仍然是AGC的主流控制方法[12-13].但传统的PID控制器不具有系统优化功能，且根据系统参数变化进行PID的动态调整不适用于实际的应用.模型预测控制(MPC)由于控制性能和鲁棒性都明显优于PID控制[14]，特别是针对具有非线性，不确定性时变及延时特点的控制对象，近年来在相关领域的研究中得到广泛关注.廖小兵等[15]提出多区域互联电网AGC系统的分布式模型预测控制，但由于MPC的控制对象是固定的数学模型，不适合在系统模型参数变化时进行控制调节.目前，通过对MPC控制器调整来应对由H引起的系统参数变化的方法并不普遍.尹子剑[16]针对非线性延时的系统，设置多个固定模型加一个可重新赋值适应模型的切换MPC方法，该方法若用于线性时变的H参数变化，会增加控制的复杂度，不利于方法的实施.

针对上述分析，本文基于风速不确定性变化对AGC系统参数造成的影响，提出一种自适应MPC方法，当H受到风速不确定性影响而发生变化时，通过控制器参数的自整定及模型变化获取更好的控制效果.

1 系统模型构建

1.1 双馈风机模型

双馈风机(DFIG)采用双馈感应电机作为发电机，由于其具有变流器容量小、成本低、变速恒频运行等优势，成为风电场中的主流发电设备，占据70%～80%的风电装机比[17].DFIG参与电网频率调节主要依靠调整其转子转速变化吸收或释放部分旋转动能实现.

风机空气动力系统的风力输出可以表示为

(1)

式(1)中：Pt为风力电机输出功率；Cp为风机性能系数；ρ为空气密度;r为风机叶片半径;V(t)为实时风速；β为桨距角；λ为旋翼叶尖速度与风速的比值，即

(2)

式(2)中：ωt为低速轴转速.因此，以Cp(λ,β)构建数学模型[18],即

(3)

根据式(3)对应的风能系数和桨距角之间的关系，需要将桨距角β置于1°附近，保持最佳尖叶速比λopt，从而获得风机性能系数Cp.

1.2 含风电的AGC动态模型的构建

一般而言，含风电电力系统进行AGC研究时，对风电有2种处理方式：1) 将风机输出等效为负荷的波动，这种方式不会考虑系统的参数动态变化；2) 风机参与系统调频，这时需要考虑风机输出的动态变化对系统的影响.

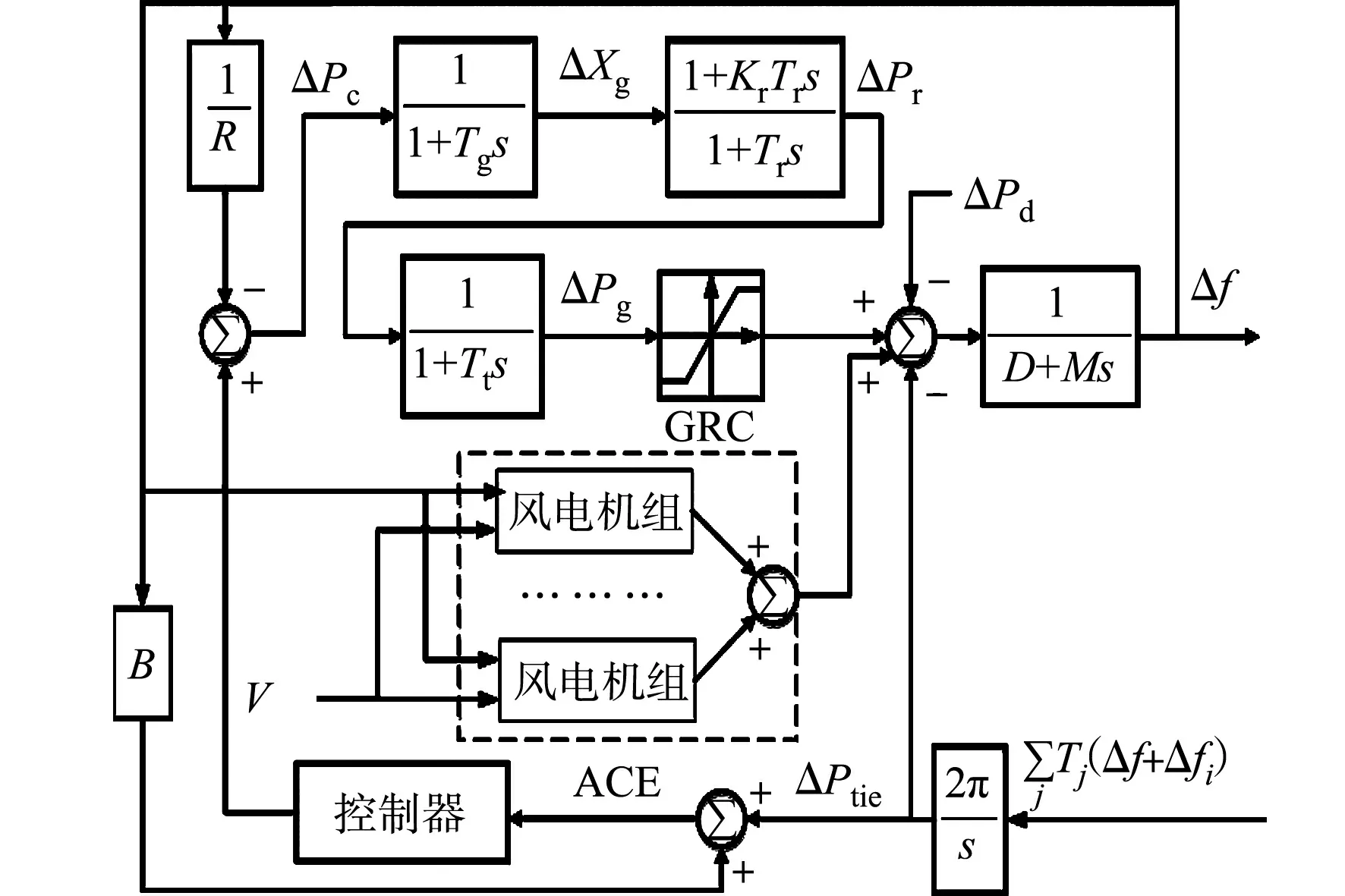
图1 单区域AGC系统结构Fig.1 Structure of single area AGC system

以两区域互联电力系统为例，对AGC方法进行研究，风机参与一次调频，各区域之间通过联络线进行功率交换.单区域AGC系统结构,如图1所示.图1中：Δf为频率偏差；ΔXg为调节阀位置偏差；ΔPtie为联络线功率偏差；M为发电机转动惯量，M=2H；D为负荷阻尼系数；Tg为调速器时间常数；ACE为区域控制偏差；ΔPg为发电机功率偏差；ΔPd为负荷扰动偏差；Kr为再热系数；Tr为再热时间常数；Tt为气容时间常数；B为频率偏差因子；R为下降速率系数;V为风速.

AGC系统的调速器单元、再热单元、汽轮机的数学描述可参见文献[15,18-19]，此处不再赘述.

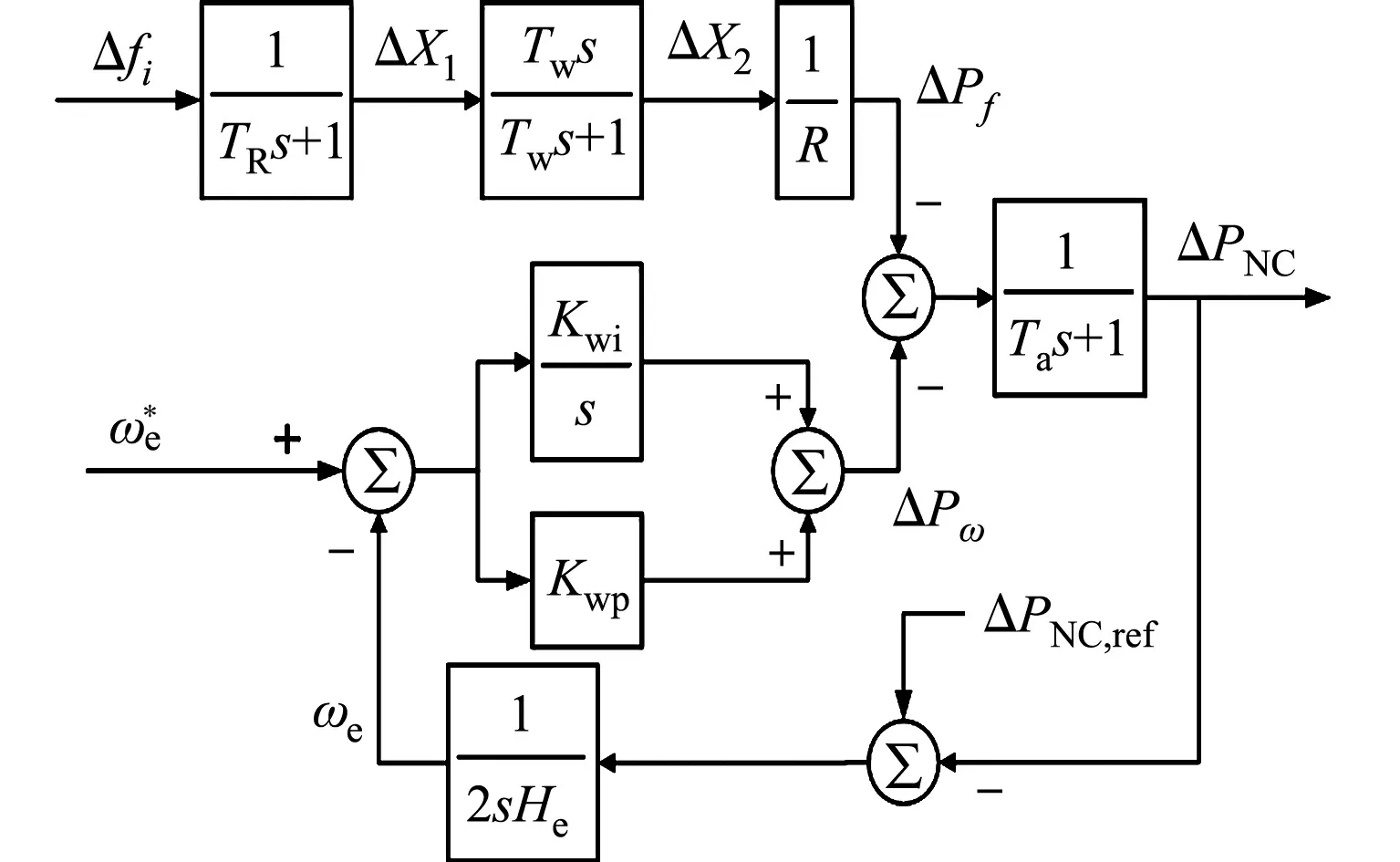
图2 双馈风机惯性控制模型Fig.2 Inertia control model of DFIG

当风电机组以虚拟惯性方式参与系统调频时，双馈风机惯性控制模型,如图2所示[19].图2中：TR为频率传感器时间常数；Tw为DFIG的Washout滤波器时间常数；He为风机等价惯性时间常数；Ta为风机时间常数；ΔX1为DFIG经传感器后的频率增量变化;ΔPf为风机功率信号;ΔPω为功率调节信号;Kwp，Kwi为PI控制器参数；ΔX2为DFIG经滤波器后的频率增量变化.

基于风速，风机控制器提供一个功率调节信号ΔPω，使发电机的转速控制在最佳转速，以产生最大功率.风机功率信号ΔPf和功率调节信号ΔPω分别表示为

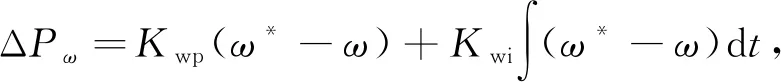
(4)

ΔPf=ΔX2/R.

(5)

2 风速变化对系统参数的影响分析

当风机以虚拟惯性方式参与系统一次调频时，风电机组通过跟踪最优转速ωref实现最大功率捕获.当惯性控制启动后，由于风电机组转速ωe改变，惯性响应过程会伴随着速度控制器进行动态调整.

考虑风速的不确定性变化，对式(2)变形，可得到转子转速与风速之间的对应关系，即

(6)

风机通过转子转速的变化吸收或释放旋转动能，以此影响风机用于参加电力系统调频的有效储能量.双馈风电机组的有效储能可以通过等效虚拟惯性时间常数反映，定义等效虚拟惯性时间常数为机组有效储能与机组额定容量的比值，并考虑风速对转子转速的影响，即

(7)

式(7)中：J为风机转动惯量；PN为风电机组额定容量.

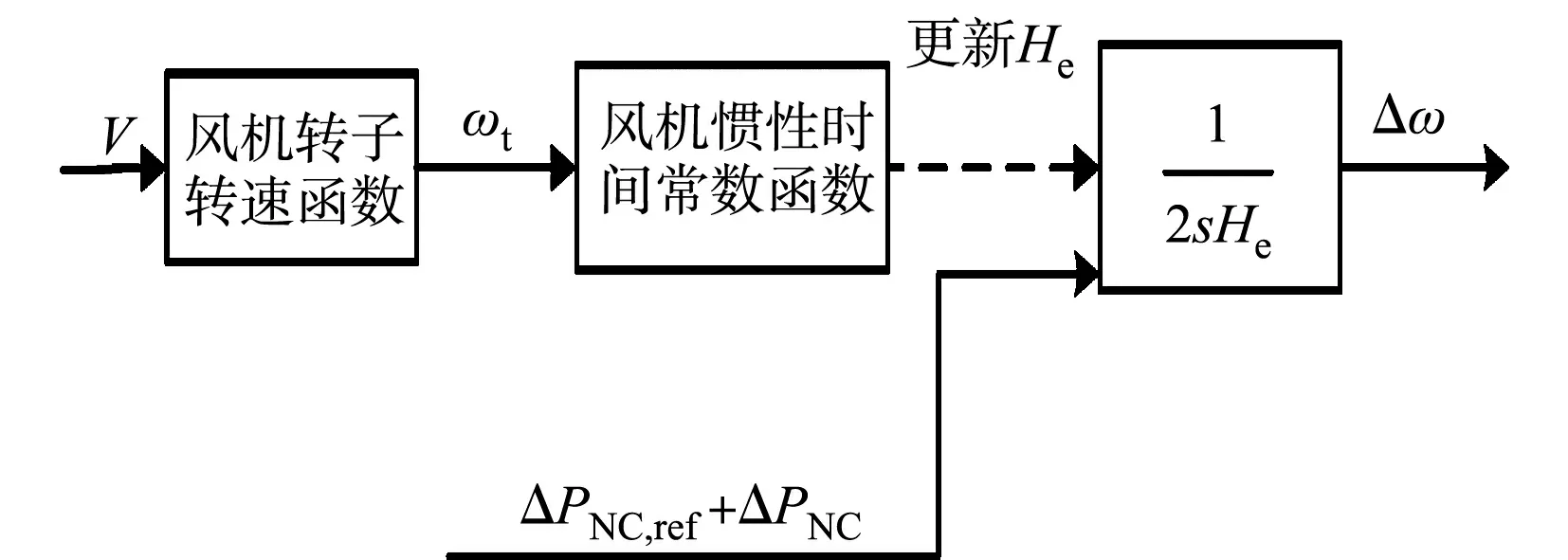
图3 双馈风机虚拟惯性时间常数的调整Fig.3 Adjustment of virtual inertia time constant of DFIG

因此，需要在此过程中对He进行调整.通过跟踪风速变化，由式(6),(7)计算出以V为变量的He函数.根据He更新风机模型中积分控制环节，使风机当前时刻的转速ωe发生变化，从而改变风机调节信号ΔPω，最终影响风机输出Pt.双馈风机虚拟惯性时间常数的调整过程,如图3所示.

根据风机虚拟惯性时间常数的定义，He的变化与风机有效吸收或释放的旋转动能有关.在考虑风机虚拟惯性时间常数He对AGC系统总惯性时间常数H的影响时，要明确风机所产生有效发电量在电力系统总发电量中的占比，风机虚拟惯性时间常数He与电力系统总惯性时间常数H之间成线性关系[5].

AGC系统惯性时间常数受到风电机组虚拟惯性时间常数影响后，有

H=m·He+Hh.

(8)

式(8)中：m为风机发电量在电力系统中所占比例;Hh为火电机组固有惯性时间常数.

由此可见，风速的不确定性变化输入会影响风电机组参数的改变，从而引起系统参数的不确定变化，给系统的输出带来动态影响.风机虚拟惯性时间常数的改变会引起系统总惯性时间常数变化，频率变化或快或慢，最终造成系统频率稳定性变差.为了解决参数变化带来的动态影响，要求系统的控制器能够适应控制对象数学模型的变化，传统MPC控制器已经不能适应这种需求.

3 自适应模型预测控制策略

3.1 预测优化原理

AGC系统中的MPC控制器由预测模型、滚动优化及校正反馈3部分构成.系统离散化方程式为

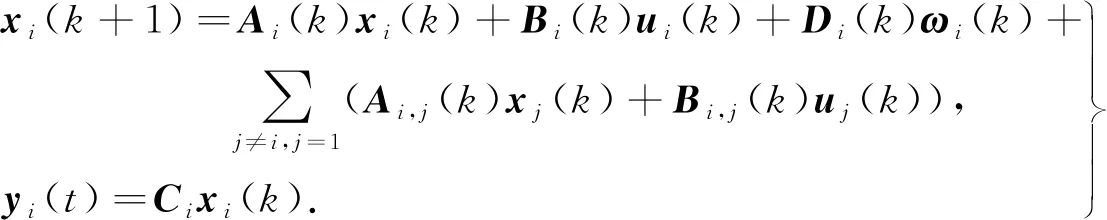
(9)

若输入序列为

(10)

可获取状态变量预测序列X和输出量的预测序列Y,即

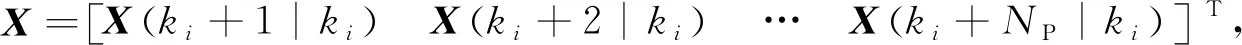
(11)

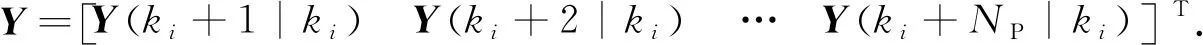
(12)

结合系统约束，设计目标函数为

J(k)=‖E(k)‖2Q+‖Δu(k)‖2R.

(13)

式(13)中：E(k)为预测输出量与未来跟踪目标参考值之间的差值形成的误差跟踪矩阵;Δu(k)为发电机功率变化率的控制序列；Q，R为对角权值系数矩阵.

按上述目标函数，可获取最优控制序列，即

(14)

将U*(k)代入式(11),可得最优输出序列，即

(15)

考虑到研究系统中风速的不确定性变化给AGC系统参数带来的影响，对模型预测控制中的误差校正提出了更高的要求.由于MPC控制器的控制对象模型不断发生变化，控制序列的不断变化使该模型已经不满足传统MPC的控制条件，这就需要对传统MPC控制器进行自适应调整.

3.2 MPC参数自整定

为了使MPC适应模型参数的变化，可以根据模型参数变化对MPC参数进行同步整定，并制定有效的选择控制策略，达到控制效果[20].在参数自整定设计过程中，经过大量仿真实验结果的统计，设计满足控制性能要求的参数自整定方式如下.

1) 控制时域Nc=(0.25～0.50)H×过程稳态时间/采样周期；

2) 预测时域Np=0.15H×过程稳态时间/采样周期；

3) 调整权值系数矩阵Q，R的变化范围为0.60～0.75；

4) 控制变量误差CVi权重=1/(CVi上限-CVi下限)；

5) 被控变量误差MVi权重=(1～3)/(MVi上限 -MVi下限)；

6) 被控变量误差增量ΔMVi权重=(1～3)/(MVi上限-MVi下限).

其中：CVi上限、CVi下限、MVi上限、MVi下限分别是MPC工具箱参数变化的上、下限范围,起到系统仿真时参数范围的限制作用.

3.3 MPC自适应控制策略

为了解决风速变化引起的参数变化对系统稳定性的影响，结合上述参数整定结果，对预测优化过程进行自适应调整.

对于新建MPC应用，一旦功能设计已经完成，就意味着对应的控制变量(MVs)、被控变量(CVs)、扰动变量(DVs)已确定.自适应控制中，一方面，对系统参数进行动态调整；另一方面，对控制域和预测域进行调整，并改变目标函数中的权值系数矩阵权重，从而消除参数变化引起的问题.

控制算法有以下6个步骤.

步骤1自动模型识别.给定初始的预测时域Np和控制时域Nc，按照模型预测控制原理，在k1时刻，根据起始时刻输入序列U(k)，从而获取预测序列X(k)和输出序列Y(k).

步骤2根据滚动优化目标函数J(k)的最小值，确定系统未来n个时刻的期望输出序列ys(k)，从而确定误差跟踪矩阵E(k).

步骤3将以上值代入目标函数，可获取最优控制序列U*(k)和输出序列Y*(k).

步骤4判断H是否发生变化，若保持不变，则重复执行步骤1～3，若发生变化，则执行步骤4.

步骤5根据获取的部分模型,控制模块执行相应子系统的参数自整定.预测过程中，到下一采样时刻，首先要检测对象的实际输出y(k+1)，并且与式(15)作对比，得到k+1时刻的输出误差，即

e(k+1)=y(k+1)-y*(k+1).

(16)

步骤6根据输入误差修正预测输出为

(17)

式(17)中:h为误差系数矩阵.因此，参数自整定后预测输出序列为

(18)

该算法可根据模型参数的变化进行参数自整定，以获取更好的控制效果.

4 仿真分析

在Matlab/Simulink环境下，对所提方法进行仿真验证.参数设置如下：仿真时间T=120 s；采样周期Ts=0.03；给定初始预测时域Np=10，Nc=3；其他参数取值，如表1所示.表1中：M为发动机转动惯量；D为负荷阻尼系数；Tr为再热时间常数；TG为调速器时间常数；Kr为再热系数;Tt为气容时间常数；B为频率偏差因子，p.u.为标幺值(下同)；R为机组调差系数；KS12为联络线区域交互增益.

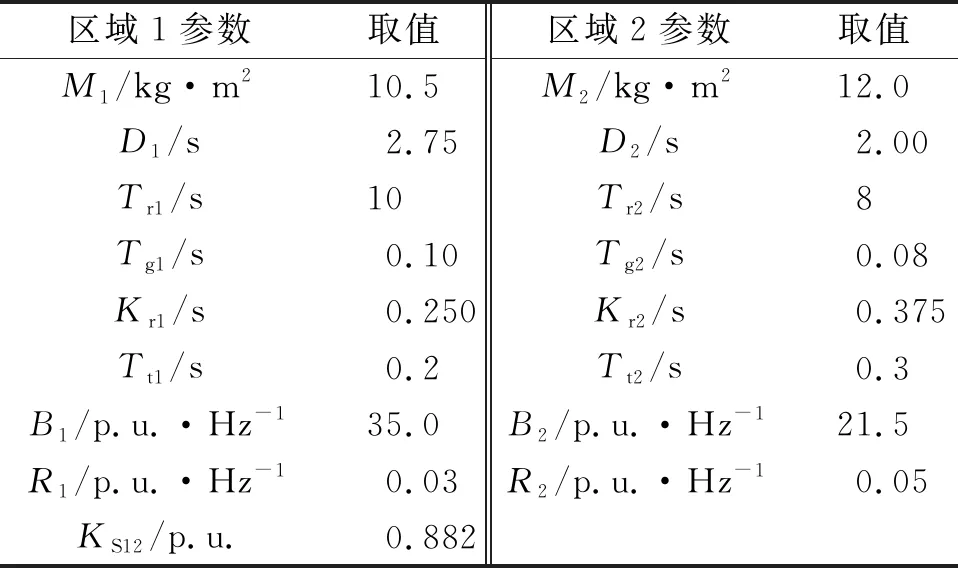
表1 两区域AGC系统参数取值Tab.1 Parameter values of AGC system in two regions

根据风电的最大功率点跟踪策略，Cp(λ,β)非常接近于0.45.考虑到预测风速V(t)，风电机叶片半径取0.05 km，空气密度ρ取1.293 kg·m-3.风电场采用80台单台5 MW机组，风电机组出力总额为400 MW，火电机组出力总额为2 600 MW，电力系统出力总额为3 000 MW.仿真中,考虑发电机变化率约束(GRC)和调速器死区(GDB)，且火电机组GRC典型值取0.001 7 MW·s-1[18].

4.1 低风速变为高风速

在t=100 s时，给区域1和区域2分别施加阶跃扰动ΔP1=0.10，ΔP2=0.06.要求区域1的风速发生变化，当t=60 s时，风速由6.0 m·s-1变为9.6 m·s-1,对应的AGC系统惯性时间常数分别为H1=5.4，H2=5.6；而区域2给定一个恒定的风速V=9.6 m·s-1.低风速变为高风速时，风机的输入及输出变化和两区域的频率偏差变化,分别如图4，5所示.图4，5中：Pt表示风机的输出功率；Δf1，Δf2分别表示区域1和区域2的频率偏差变化量.

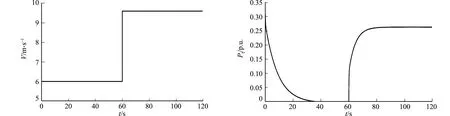
(a) 风机输入 (b) 风机输出图4 低风速变为高风速时风机的输入及输出变化Fig.4 Changes of wind turbine input and output when low wind speed changes to high wind speed

(a) 区域1 (b) 区域2图5 低风速变为高风速时两区域的频率偏差变化Fig.5 Variation of frequency deviation between two regions when low wind speed changes to high wind speed

由于两区域之间联络线的影响，使区域2恒风速条件下的控制效果受到区域1风速变化的影响，因此，在区域2中，频率偏差在60 s处也出现了波动，但其影响效果远小于区域1中风速变化的影响.

在风速由低变高的过程中，由于参数H增大，使风速波动对系统频率产生较大的影响，体现在频率偏差变化幅度的增加，超调量增大.由图5可知:加入自适应MPC控制策略后，能有效地抑制这种现象，使频率偏差的变化效果得到显著优化;对于100 s时由于负荷变化引起的频率变化，该控制策略能有效地减小频率偏差曲线的波动幅度和超调量.

定义风速波动稳定时间为TF，负荷波动稳定时间为TL.在区域频率偏差变化中，由风速变化引起的频率偏差定义为ΔfF，负荷波动引起的频率变化定义为ΔfL.低风速变为高风速时的系统仿真结果，如表2所示.

表2 低风速变为高风速时的系统仿真结果Tab.2 System simulation results when low wind speed changes to high wind speed

4.2 高风速变为低风速

在t=100 s时，给区域1和区域2分别施加阶跃扰动ΔP1=0.10，ΔP2=0.06.要求区域1的风速发生变化，当t=60 s时，风速由9.6 m·s-1变为6.0 m·s-1,对应的AGC系统总惯性时间常数分别为H1=5.6，H2=5.4；而区域2给定一个恒定的风速V=9.6 m·s-1.高风速变为低风速时，风机的输入及输出变化和两区域的频率偏差变化，分别如图6,7所示.

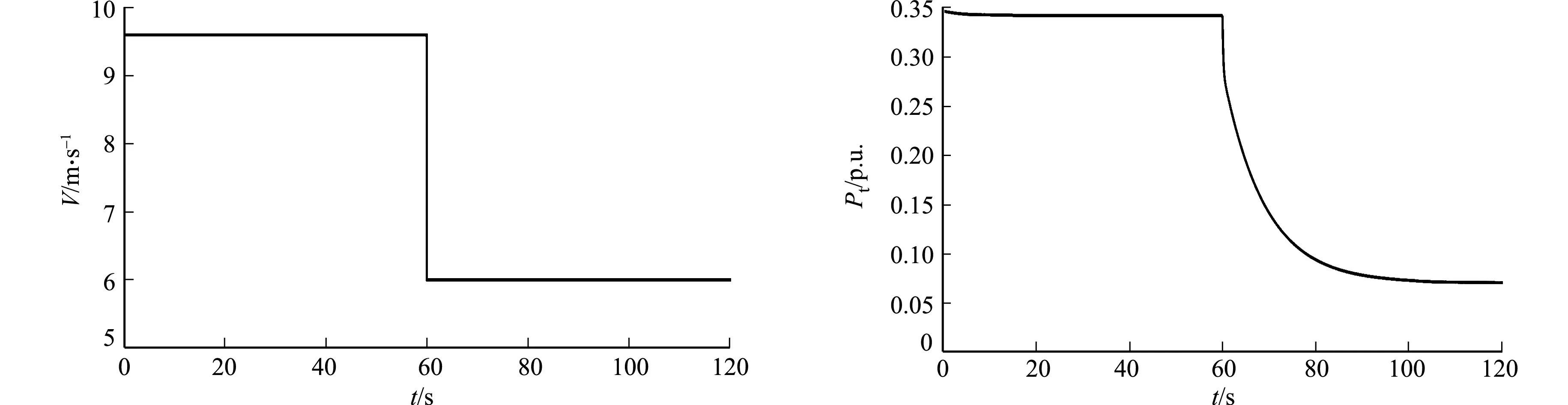
(a) 风机输入 (b) 风机输出图6 高风速变为低风速时风机的输入及输出变化Fig.6 Changes of wind turbine input and output when high wind speed changes to low wind speed

(a) 区域1 (b) 区域2图7 高风速变为低风速时两区域的频率偏差变化Fig.7 Variation of frequency deviation between two regions when high wind speed changes to low wind speed

在风速由高变低的过程中，参数H减小.根据H对系统机械性能的物理影响，与高风速下控制效果相比，H的减小会使风机输出对频率波动造成的影响有所减弱.由图7可知：该策略对风电变化所引起频率波动的调整效果并不明显.但从100 s负荷的变化情况可见，加入控制策略后，通过控制器的调整，对负荷变化造成的影响进行抑制，频率偏差控制效果得到了优化.仿真结果验证了该自适应控制策略的有效性.

高风速变为低风速时的系统仿真结果,如表3所示.