利息率理论的建构研究

李 翀，张世铮

(北京师范大学 经济与工商管理学院，北京 100875)

一、经典利息率理论的回顾

(一)魏克赛尔的利息率理论

在经济思想史发展过程的每一个历史阶段，经济学家们都对利息率展开研究。经典的利息率理论主要有魏克赛尔的利息率理论、凯恩斯的利息率理论和罗伯逊的利息率理论，笔者以这三种经典利息率理论为基础来讨论利息率决定问题。

瑞典经济学者魏克赛尔(Knut Wicksell)在1898年出版了名为《利息与价格》的著作，提出了很长一段时间在经济学界具有重要影响的利息率理论。

魏克赛尔区分了自然利率和贷款利率两个概念。他写道：“贷款中有某种利率，它对商品价格的关系是中立的，既不会使之上涨，也不会使之下跌。这与如果不使用货币、一切借贷以实物资本形态进行、在这样情况下的供求关系所决定的利率，必然相同。我们把这个称之为资本自然利率的现时价值，其含义也是一样的。”(1)〔瑞典〕魏克赛尔：《利息与价格》，蔡受百等译，北京：商务印书馆，1982年版，第63页。

按照魏克赛尔的解释，借资资金的供给是存款，借贷资金的需求是投资。假定所有企业家都没有资本，他们借入资金雇佣工人、购买原材料和租用土地进行生产，在扣除了自己才干的收入之后需要向提供资金的资本家支付的利息率就是资本自然利率。资本自然利率是由资本的需求和供给决定的。魏克赛尔指出，如果贷款利率低于自然利率，企业家将获得超额利润，他们将扩大生产，从而导致对劳动和原材料需求的增加，进而导致商品价格的上升。相反，则导致商品价格的下降。

按照魏克赛尔的理解，自然利率取决于生产的效率、固定和流动资本的数量、劳动和土地的供给。贷款利率与自然利率的准确吻合是不存在的。自然利率的变化是持续的和不间断的，贷款利率是不连续的和跳跃的。(2)〔瑞典〕魏克赛尔：《利息与价格》，蔡受百等译，第84-86页。

在这个时期，除了魏克赛尔的利息率理论以外，还有马歇尔(Alfred Marshall)在1890年出版的《经济学原理》中提出的利息率理论和费雪(Irving Fisher)在1907年出版的《利息理论》中提出的利息率理论。他们与魏克赛尔相似，都是从资本与投资的角度分析利息率的决定。

(二)凯恩斯的利息率理论

英国经济学者凯恩斯(J.M.Keynes)在1936年出版了代表作《就业、利息和货币通论》，提出了被经济学界称之为的现代货币理论。

凯恩斯认为：“利息率是放弃流动性的报酬。”(3)③ 〔英〕凯恩斯：《就业、利息和货币通论》，宋韵声译，北京：华夏出版社，2012年版，第129、151-197页。所谓流动性是指货币或者近似于货币的资产。由于货币随时可以被用于支出，它具有高度的流动性。当人们放弃流动性的时候，他们需要得到回报，这种回报就是利息。

凯恩斯指出，利息率是由货币的需求和货币的供给决定的。在凯恩斯看来，人们之所以需要货币是因为人们偏好货币的流动性，他把货币需求函数称为流动性偏好函数。他认为，人们对货币的需求有三个动机：交易动机即买卖东西的动机、谨慎动机即预防发生不测事件的动机、投机动机即买卖债券的动机。在交易和谨慎动机下对货币的需求量取决于国民收入，国民收入越高，交易量就越大，可能发生的意外支出就越多，货币需求量就越大。在投机动机下对货币的需求量取决于利息率，利息率越高，债券价格越低，人们倾向于买进债券，为了投机而持有的货币将减少。

设M1为满足交易动机和谨慎动机所持有的现金数量，M2为满足投机动机所持有的现金数量，Y是国民收入，r为利息率，那么货币需求函数是：

M=M1+M2=L1(Y)+L2(r)

(1)

另外，凯恩斯还认为，货币供给是政府的货币政策决定的。在货币需求不变的条件下，如果货币供给增加，货币供过于求，利息率将下降；如果货币供给减少，货币供不应求，利息率上升。③

(三)罗伯逊的利息率理论

英国经济学者罗伯逊(Dennis Robertson)是凯恩斯的学生，后来又同在剑桥大学任教，但是罗伯逊与凯恩斯发生了分歧，并提出了与凯恩斯不同的利息率理论。罗伯逊在1940年出版的《货币理论文集》中指出，利息率不是由货币的需求和供给决定的，而是由可贷资金的需求和供给决定的。

可贷资金的需求包括投资需求和窖藏需求。投资需求是出于投资的目的而形成的对资金的需求，窖藏需求是为了储藏价值而形成的对资金的需求。由于利率越高，投资和窖藏的成本越高，可贷资金的需求量就越少，它是利率的函数。如果用Md表示可贷资金的需求量，用I表示投资，用ΔH表示窖藏增量，用i表示利息率，那么可贷资金的需求函数可以表达为：

Md=I(i)+ΔH(i)

(2)

另外，可贷资金的供给量包括储蓄的供给量和货币供给增量。利息率越高，储蓄收益越高，储蓄数量就越大。但货币供给取决于货币政策，它不受利息率影响。因此，可贷资金储蓄数量是利息率的函数。如果用Ms表示可贷资金的供给量，用S表示储蓄数量，用ΔM表示货币供给的增量，那么可贷资金的供给函数可以表达为：

Ms=S(i)+ΔM

(3)

如图1所示，纵轴表示利息率，横轴表示可贷资金的数量。当投资需求曲线与储蓄供给曲线相交的时候，投资对可贷资金的需求量等于储蓄对可贷资金的供给量，形成了自然利率in，罗伯逊把它称为基础性利率。当可贷资金需求曲线与可贷资金供给曲线相交的时候，可贷资金需求量等于可贷资金供给量，形成了市场利率im。(4)D.Robertson，Essays in Monetary Theory，London:P.S.King & Son，1940.

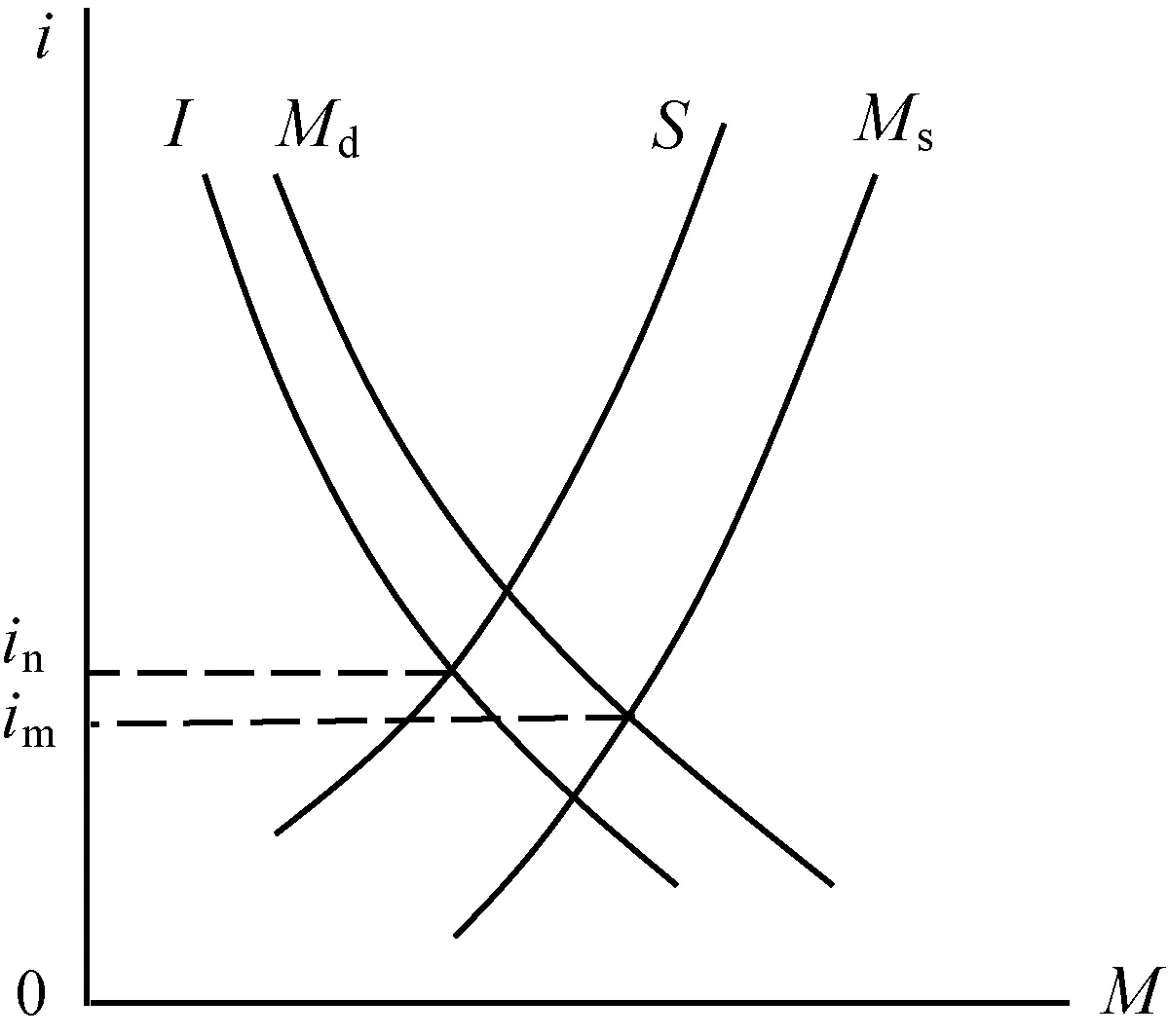
图1 利息率的决定

(四)现行的利息率理论

在罗伯逊以后，利息率理论的研究没有实质性的进展，有的经济学者深化了前述利息率理论的分析，有的经济学者则是以不同的表达方式复述前述的利息率理论。

美国经济学者法博齐(Frank J.Fabozzi)和莫迪利亚尼(Franco Modigliani)在1996年出版的被称为是金融学经典教科书的《资本市场》中指出，利息率是借方为在一定期限内使用某种资源而支付给贷方的价格，它是由投资形成的资金需求和储蓄形成的资金供给决定的。他们认为，生产者总是按照利润最大化的原则选择最优投资量来进行生产，最优的投资量与他们拥有的资金的差额形成了他们对资金的需求量。另外，消费者总是根据效用最大化的原则选择最优储蓄量进行消费，他们拥有的资金与最优储蓄量的差额形成了他们对资金的供给量。

生产者对资金的需求量是利息率的函数，利息率越高，资金需求量越小。消费者对资金的供给量是利息率的函数，利息率越高，资金供给量越大。当资金需求量大于资金供给量时，利息率上升；当资金需求量小于资金供给量时，利息率下降；当资金需求量等于资金供给量时，决定了均衡的利息率。他们把这种利息率称为基础利息率。(5)〔美〕法博齐、莫迪利亚尼：《资本市场》，唐旭等译，北京：经济科学出版社，1998年版，第361-377页。

美国经济学者斯蒂格利茨(Joseph E.Stiglitz)在1993年出版的被称为经典经济学教科书的《经济学》中指出，利息率是货币的时间价值，即货币未来价值和现在价值的差价，它是由可贷资金的需求和供给决定的。借入资金的数量随着利息率的上升而减少，贷出资金的数量随着利息率的上升而增加，当可贷资金的需求量等于供给量的时候，形成了均衡的利息率。(6)〔美〕斯蒂格利茨：《经济学》，上册，高鸿业等译，北京：中国人民大学出版社，1997年版，第117-120页。

美国经济学者萨缪尔森(Paul A.Samuelson)和诺德豪斯(William D.Nordhaus)在2010年出版的第19版《经济学》是目前最流行的经济学教科书，他们在该书中指出利息率是提供资本的收益率，然后从实物形态资本的角度分析了短期和长期利息率的决定。

萨缪尔森和诺德豪斯认为，在短期里，资本的供给是固定的，它无法由于利息率的提高而增加。资本的需求量取决于资本的边际产品，即增加一单位资本所带来的产品，它就是资本的收益率。在边际收益递减规律影响下，资本数量越大，资本收益率就越低。当资本的需求量等于资本供给量时，资本的收益率等于利息率，资本需求方得到了最大的收益，他们不再增加资本需求量，从而决定了均衡的收益率和利息率。如图2所示，纵轴表示收益率或利息率，横轴表示资本存量，DD曲线是资本需求曲线，SS曲线是资本供给曲线，两条曲线相交，形成均衡的短期利息率。

在长期里，资本可以积累，资本供给量不是固定的，利息率越高，资本的供给量越大。资本的需求量仍然取决于资本的收益率，资本越多，资本收益率越低。同样，当资本需求量等于资本供给量时，决定了均衡的收益率和利息率。如图3所示，DD曲线仍是资本需求曲线，SS曲线是资本供给曲线，两条曲线相交形成均衡的长期利息率。(7)〔美〕萨缪尔森、诺德豪斯：《经济学》，上册，萧琛译，北京：商务印书馆，2012年版，第490-498页。

图2 短期利息率的决定

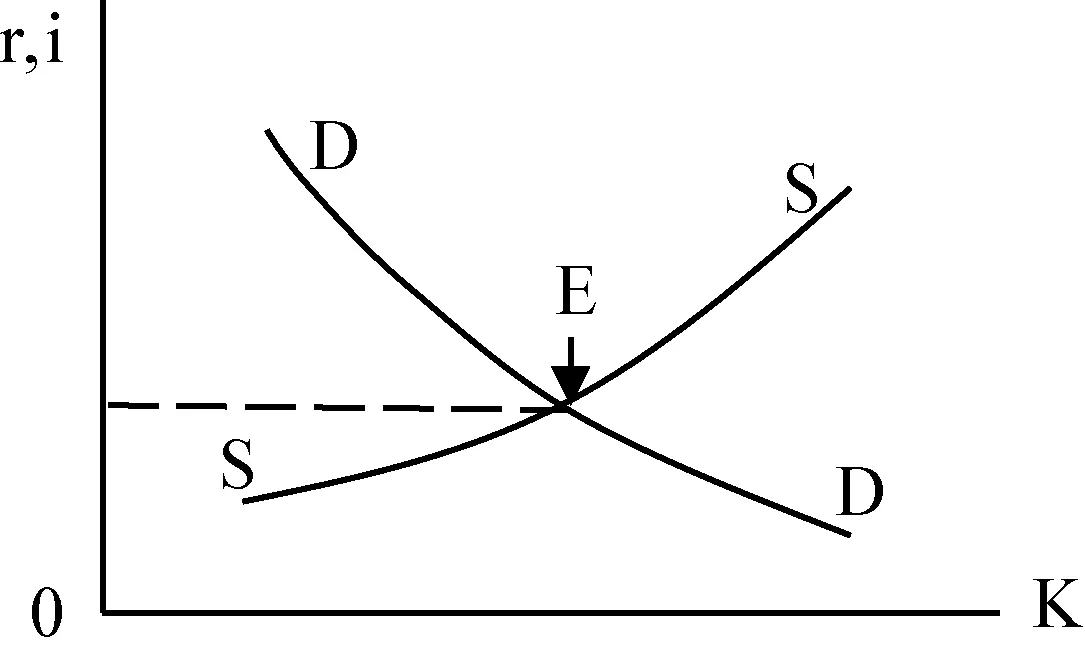
图3 长期利息率的决定

二、对经典利息率理论的逻辑分析和实践检验

(一)对经典利息率理论的逻辑分析

1.对魏克赛尔利息率理论的评论

魏克赛尔利息率理论的贡献是提出了自然利息率的概念，从而抽象出存款和投资两个基本因素来分析基础利息率的决定，摆脱了借贷市场上各种错综复杂现象的困扰，以探讨利息率决定的核心问题。他注重投资需求的作用，指出自然利息率是由在没有资本的条件下投资的利润率决定的，这种分析至今仍然具有价值。

魏克赛尔以及后来的马歇尔和费雪等经济学者处于金本位制时代，他们都没有提及货币供给因素。在金本位制条件下，货币的数量是由黄金的数量决定，因而货币供给是相对稳定的，它没有对利息率产生明显的影响。另外，当时政府奉行预算平衡的原则，政府对借贷资金的需求也不大。因此，魏克赛尔的利息率理论与他所处的时代是相适应的。但是，现在信用货币制度已经取代金本位制，借贷资金的供给和需求因素都发生了很大的变化，因而需要在新的历史条件下补充魏克赛尔的利息率理论。

2.对凯恩斯利息率理论的评论

凯恩斯与魏克赛尔不同，他处在金本位制解体的时期。英国于1931年废除了金本位制，实行信用货币制度。在信用货币制度下，货币当局拥有发行货币的权利，货币供给对利息率产生明显的影响。凯恩斯利息率理论进步的地方在于引入货币供给因素,反映货币供给对利息率的影响。但是，他认为利息率由货币的需求和供给决定的观点并不准确。在这个问题上，凯恩斯以前以及以后的经济学者都是对的。利息率是在借贷市场产生的一种现象，货币本身不是借贷资金，它只有进入借贷市场才成为借贷资金，从而才有可能对利息率产生影响。在一般情况下，货币供给变化会导致借贷资金供给变化，但借贷资金供给的变化并不是全部来自货币供给变化。这就是说，由于货币供给是货币当局决定的，借贷资金供给有外生性的一面，但是也有内生性的一面。实际上，货币当局以前发行的货币在社会上流通和借贷，即使货币当局不改变货币供给量，人们也会根据经济的变化调整借贷资金的供给量。

3.对罗伯逊利息率理论的评论

罗伯逊利息率理论比凯恩斯利息率理论准确的地方，在于他坚持认为利息率取决于借贷资金的需求和供给。但是，他也吸收了凯恩斯利息率理论中货币供给的分析，从而反映了信用货币制度下的新现象。罗伯逊指出可贷资金的供给量取决于储蓄和货币供给，指出影响利息率的供给因素既有内生性的一面，也有外生性的一面，因而是一种比较全面的利息率理论。

但是，罗伯逊利息理论存在下述不足：其一，他认为窖藏需求量是可贷资金需求量的一个组成部分，而所谓窖藏需求是保留货币的需求，居民和厂商借进资金然后把它保留下来不是普遍的现象，这说明罗伯逊受到凯恩斯提出的谨慎动机的影响，但是凯恩斯分析的是货币的需求，罗伯逊分析的是借贷资金的需求。其二，在现代经济条件下，借贷资金的需求不仅来自投资需求，而且来自消费需求和政府需求。在罗伯逊所处的时代，如果说政府的借贷需求还不明显，那么消费对借贷资金的需求应该是比较明显的了。

4.对现行利息率理论的评论

战后，利息率理论的研究没有实质性的进展。法博齐和莫迪利亚尼在利息率理论方面的贡献主要是方法上的贡献，他们从即期消费和未来消费的最优选择推导出最优储蓄，建立了储蓄函数；然后用生产函数推导出最优投资，建立了投资函数；最后用储蓄函数和投资函数分析利息率的决定。因此，法博齐和莫迪利亚尼在论证方法上比魏克赛尔要更加精确和完美，但是他们在借贷资金供给的分析中忽略了凯恩斯利息率理论进步的地方，也就是罗伯逊利息率理论坚持的地方——货币供给对利息率的影响。另外，他们在借贷资金需求的分析中只强调了投资需求，同样忽略了在现代经济中已经变得十分明显的消费需求和政府需求。

斯蒂格利茨在《经济学》中有关利息率的分析是教科书式的表述，他的分析没有罗伯逊的分析深入和全面。萨缪尔森和诺德豪斯对利息率的分析则基本停留在费雪在1907年出版的《利息率》的表述上，他们的缺陷在于只从资本存量的角度分析利息率的决定，重点分析了影响借贷资金需求和供给的资本因素，与凯恩斯和罗伯逊的利息率理论相比都后退了。

(二)对经典利息率理论的实践检验

1.对借贷资金需求因素的检验

考虑到不同国家有不同的国情，笔者选取了东西方两个典型的发达国家美国和日本的统计数据来考察借贷资金的需求情况。借贷资金主要有两种形态：一种是银行信贷，另一种是债务工具。

美国借贷资金的需求来自居民、企业、政府、金融机构和境外，居民对借贷资金的需求主要包括消费信贷和不动产抵押贷款，企业对借贷资金的需求主要出于经营和投资的目的，政府对借贷资金的需求主要出于弥补财政赤字的需要。由于金融机构存在相互借贷的行为，笔者又主要考察发达国家境内的借贷情况，因而把金融机构和境外对借贷资金的需求排除在外。

考虑到年与年之间对借贷资金的需求有可能发生较大的变化，笔者选取了数据可比的1981—1985年以及2011—2015年两段时期美国的年平均借贷资金需求量来观察借贷资金需求情况的变化，如表1所示。表中的借贷资金包括银行信贷和债务工具，债务工具包括政府债务凭证和企业债务凭证，政府债务凭证包括国库券和政府债券，企业债务凭证只包括公司债券。表中的数据是年末余额，年与年之间余额的变化表示新增加的贷款额减去该年偿还的贷款额之差。

从表1可以看到，美国对借贷资金的需求来自居民需求、企业需求和政府需求。2011—2015年与1981—1985年相比，居民对借贷资金需求的比例保持稳定，企业对借贷资金需求的比例出现较大幅度下降，政府对借贷资金需求的比例发生较大幅度上升。

按照同样的方法，笔者选取了数据可比的1978—1982年和2011—2015年两段时期日本年平均借贷资金需求量来观察借贷资金需求情况的变化，如表2所示。表中的借贷资金仍然包括银行信贷和债务工具。

从表2可以看到，日本对借贷资金的需求同样来自居民需求、企业需求和政府需求。2011—2015年与1978—1982年相比，居民对借贷资金需求的比例有所上升，企业对借贷资金需求的比例大幅度下降，政府对借贷资金需求的比例大幅度上升。总体来看，日本居民借债意愿远弱于美国。

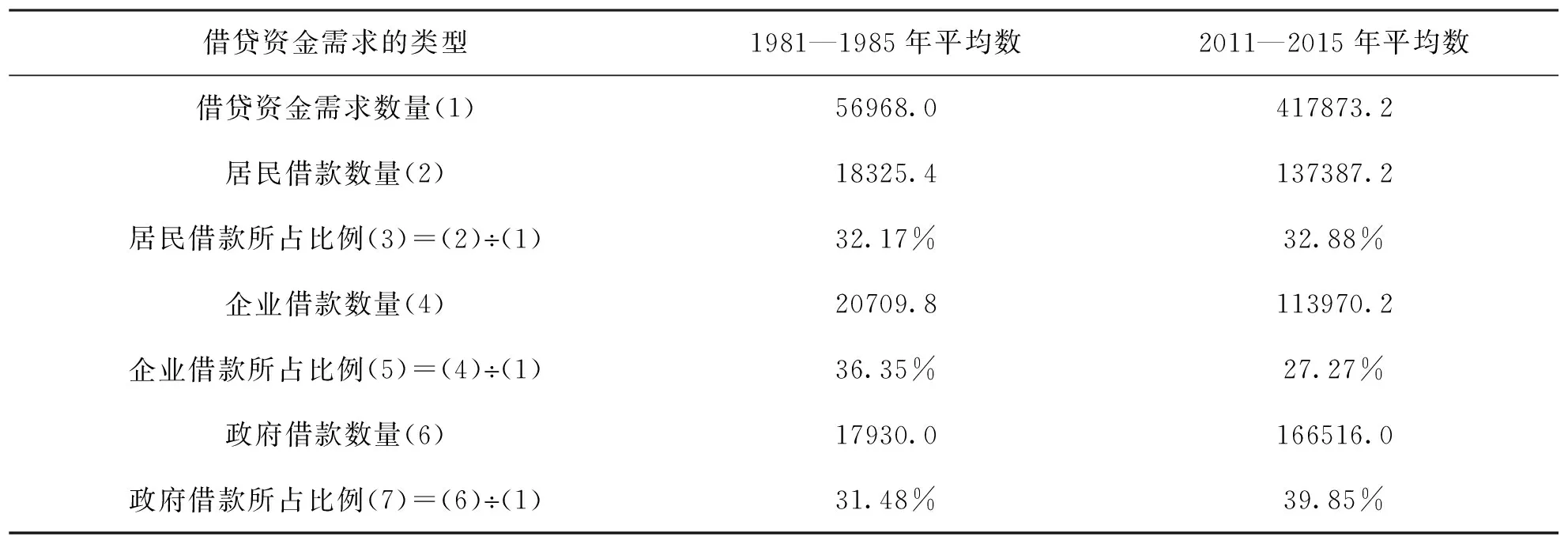
表1 美国借贷资金的需求情况 单位：亿美元

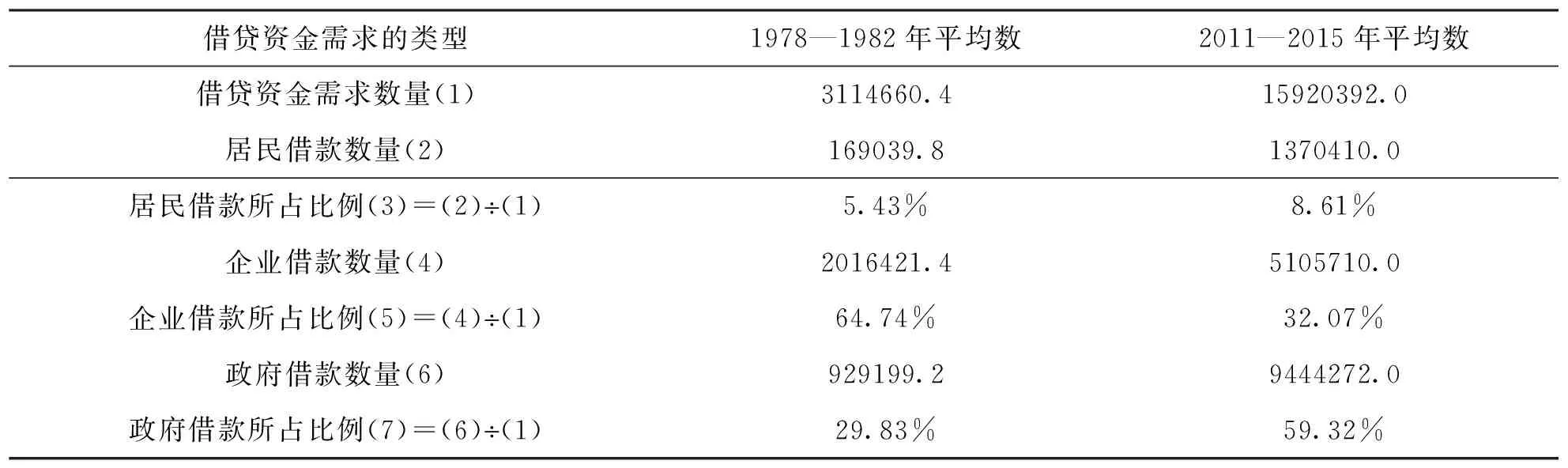
表2 日本借贷资金的需求情况 单位：亿日元

综合美国和日本两国的实际情况可以证实，经济学者们强调借贷资金的投资需求是正确的。生产是第一性的，如果一个社会不创造出新的财富，借贷市场很难健康发展。在美国，居民借款主要组成部分是住房抵押贷款，在2015年住房抵押贷款占居民借款的66.78%，占整个社会债务的21.10%。在经济学中住房属于投资品，对住房抵押贷款的需求属于投资需求。这样，即使在美国工业化后期的2011—2015年，投资需求占整个借贷资金需求的48.37%(=21.10%+27.27%)。在日本，即使不算住房抵押贷款，在工业化如火如荼的1978—1982年，投资需求占整个借贷资金需求的64.74%。在工业化后期的2011—2015年，如果加上住房抵押贷款的需求，投资需求占整个借贷资金需求的40.47%(=8.40%+32.07%)。借贷资金的投资需求具有重要地位。

但是，从美国和日本的实际情况也可以看到，经典的利息率理论在分析利息率的时候，都忽略了居民对借贷资金的消费需求和政府对借贷资金的需求。消费借款需求在西方发达国家占据重要的地位，政府借款需求在所有的发达国家中发挥越来越大的作用，忽略了这两种需求显然不能解释利息率的变化情况。在2011—2015年，美国和日本居民借款对全部债务的比例分别为32.88%和8.61%，美国和日本政府借款对全部债务的比例分别为39.85%和59.32%。借贷资金的消费需求和政府需求已经成为决定利息率的基本因素。

2.对借贷资金供给因素的检验

借贷资金的供给来自居民、企业，政府、金融机构和境外。美国和日本只有银行存款来源的统计数据而没有债务工具买方的统计数据，所以这里只考察银行贷款的资金来源。如果不考虑境外资金供给，2016年美国和日本银行贷款的资金来源如表3和表4所示。

正如表3和表4所示的，从银行贷款资金来源来看，美国和日本惊人相似，居民和企业是银行贷款资金供给的主要来源，居民和企业的存款构成社会储蓄供给。货币当局的货币供给也会通过各种渠道转化为银行贷款的资金来源。经典利息率理论对借贷资金供给函数的分析是符合实际情况的。

表3 美国银行贷款的资金来源 单位：亿美元

表4 日本银行贷款的资金来源 单位：亿日元

三、新利息率理论的建构

(一)借贷资金的需求函数

在对经典的利息率理论进行逻辑分析和实践检验以后，笔者认为有必要对经典利息率理论进行补充，构建更加符合现代现实经济情况的利息率理论。应该指出，利息率是一个庞大的体系，利息率有政策性利息率和非政策性利息率之分，有实际利息率和名义利息率之分，有不同期限的利息率之分，有不同风险程度的利息率之分，如此等等。但是，在理论上分析的利息率是由基本供求因素决定的利息率，是一种基础利息率。

首先来考察借贷资金的需求函数。借贷资金需求量的第一个组成部分是消费需求量。笔者在前面曾经指出，在经济学中住房属于投资品。但是，这只是经济学者们的一个定义。从消费者的角度来看，借款购买住宅与借款购买其他耐用消费品没有什么区别。另外，住房抵押贷款的决策过程与居民消费信贷的决策过程是相似的，都取决于利息率的高低和对未来收入的预期。因此，笔者把住房抵押贷款看作是对借贷资金的消费需求。这样，借贷资金的消费需求量包括对一般消费信贷的需求量和对住房抵押贷款的需求量。借贷资金的消费需求量取决于利息率和预期的收入，利息率越高，居民借入资金的成本越高，借贷资金的消费需求量就越小。另外，预期收入越高，居民未来偿还贷款的能力越强，借贷资金的消费需求量就越大。考虑到居民的总收入与产值接近于成比例变化，在建立借贷资金需求函数的时候可以用预期产值取代预期收入。

借贷资金需求量的第二个组成部分是投资需求量，即各个产业出于经营的需要而形成的对借贷资金的需求量。借贷资金的投资需求量取决于利息率和预期的利润率。利息率越高，投资的成本越高，对借贷资金的投资需求量就越小。另外，预期利润率越高，投资的预期收益越高，对借贷资金的投资需求量就越大。

借贷资金需求量的第三个组成部分是政府需求量，即政府为了弥补财政赤字而形成的对借贷资金的需求量。借贷资金的政府需求量取决于政府的财政赤字状况，财政赤字越大，借贷资金的政府需求量就越大。但是，借贷资金的政府需求量对利率的反应不敏感。

因此，如果用CD_D表示借贷资金的需求量，用I表示投资需求量，用C表示消费需求量，用G表示政府需求量，用i表示利率，用ye表示预期产值，用re表示预期利润率，用d表示财政赤字，那么借贷资金需求函数可以表达为：

CD_D=I(i,re)+C(i,ye)+G(d)

(4)

假定预期产值、预期利润率、财政赤字不变，借贷资金的需求量与利息率存在着反方向变化的关系：利息率越低，借贷资金的需求量越大。在以纵轴表示利息率、横轴表示借贷资金需求量的坐标系里，借贷资金需求曲线表现为一条向右下方倾斜的曲线，如图4中的曲线CD_D所示。

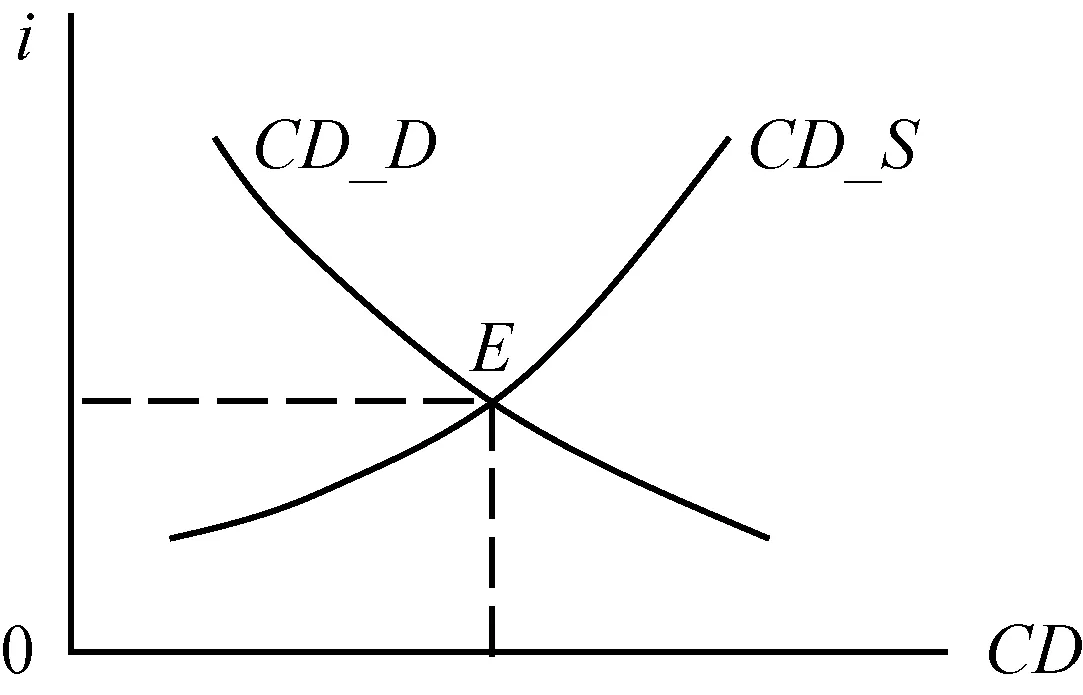
图4 利息率的决定

(二)借贷资金的供给函数

借贷资金的供给来自居民的储蓄、企业的储蓄和货币供给量。如果把居民和企业的储蓄称为社会储蓄，那么社会储蓄的供给量受利息率影响，利息率越高，社会储蓄就越高，社会储蓄供给量就越大。另外，社会储蓄供给量还受现期产值影响，现期产值越大，居民和企业总收入越高，社会储蓄供给量就越大。

货币供给量取决于货币当局的货币政策，它不受利息率影响。货币当局会通过调整法定准备金比率、调整贴现率、公开市场操作，调整对银行的政策性利率的方法影响货币供给量。但是，正如笔者在前面指出的，货币供给的增量并不必然构成借贷资金供给的增量。在货币当局通过最常用的买进政府证券的方式投放货币的情况下，由于交易一般通过银行转账的方式进行，卖出政府证券的个人或机构在商业银行的存款将增加。如果商业银行保留超额准备金，这部分货币没有转变为借贷资金。只有在商业银行相应增加贷款的情况下，才会导致借贷资金供给的增加。因此，货币供给量只有一部分进入到借贷市场而成为借贷资金的供给量。在正常的经济情况下，货币供给转变为借贷资金的比例较大。在经济衰退特别是陷入流动性陷阱的情况下，货币供给转变为借贷资金的比例较小。另外，居民和企业持有的现金都属于货币供给，但不属于借贷资金的供给。

这样，如果用CD_S表示借贷资金的供给量，用S表示社会储蓄供给，用M表示货币供给量，用i表示利率，用y表示现期产值，用p表示货币政策，那么借贷资金供给函数可以表达为：

CD_S=S(i,y)+M(p)

(5)

假定产值和货币政策不变，借贷资金的供给量与利息率成正方向变化：利息率越高，借贷资金供给量越大。在以纵轴表示利息率、横轴表示借贷资金供给量的坐标系里，借贷资金供给曲线表现为一条向右上方倾斜的曲线，如图4中的曲线CD_S所示。

(三)利息率的决定和变化

如图4所示，在借贷资金需求曲线与供给曲线相交的时候，借贷资金的需求量等于供给量，形成了均衡的利息率。这样决定的利息率是基础利息率，即不考虑风险、期限、内嵌权利等市场因素条件下的利息率。

前面的分析是在产值、财政赤字、货币政策为一定的条件下进行的。如图5所示，如果预期产值增加了，或者预期利润率提高了，或者财政赤字增加了，借贷资金的需求将会增加，需求曲线CD_D向右移动到CD_D1，从而导致均衡利息率的上升；相反，则导致均衡利息率的下降。同样，如果现期产值增加了，或者货币供给增加了，借贷资金的供给将会增加，供给曲线CD_S向右移动到CD_S1，均衡利息率将会下降；相反，均衡利息率将会上升。如果借贷资金的需求和供给同方向变化，它们对利息率的影响取决于它们相互抵消以后的净影响。

图5 利息率的变化

四、新利息率理论的计量分析

(一)计量方法与模型构建

1.计量方法

应该指出，利息率理论分析的是一般意义上的利息率，而实证检验使用的是不同期限、不同风险程度的名义利息率数据，所以实证检验主要是对利息率理论的主要特征进行检验。由于时间序列数据可能是非平稳的，使用简单的OLS方法容易产生伪回归现象，因此需要采用协整方法来分析非平稳经济变量之间是否存在长期稳定的均衡关系。传统的协整方法有EG两步法和JJ检验法等。但上述方法只适用于具有同阶单整的非平稳变量，而且在小样本情况下会出现估计偏误。针对以上不足，佩沙兰(M.H.Pesaran)等人提出了一种基于自回归分布滞后模型(ARDL Model)的边限协整检验方法(bounds testing)(8)M.H.Pesaran，Y.Shin and R.J.Smith，“Bounds Testing Approaches to the Analysis of Level Relationships”，Journal of Applied Econometrics,2001，16(3),pp.289-326.。该方法具有以下优势：第一，只要变量单整阶数小于2，ARDL边限协整检验法既适用于同阶I(0)或I(1)变量，也适用于单整阶数不同的变量。第二，ARDL边限协整检验法能减轻多重共线性及序列相关问题，统计性质更优。第三，相比于EG两步法和JJ协整检验法，ARDL边限协整检验法对于小样本数据的估计更有效。因此，笔者采用ARDL边限协整检验法对借贷资金需求函数和供给函数进行实证分析。

2.模型构建

为了估计借贷资金需求量与各影响因素之间的关系，笔者将新利息率理论中的借贷资金需求函数表示为如下线性静态形式：

(6)

其中ε为残差项，α为常数项，下标t表示时间。

与此类似，对借贷资金供给函数也建立如下线性实证模型：

lnCD_St=β+β1it+β2lnyt+β3lnMt+μt

(7)

其中μ为残差项，β为常数项。

根据佩沙兰等人提出的方法，为了对借贷资金需求量与其影响变量之间的关系进行边限协整分析，可在模型(6)的基础上构建相应的ARDL模型：

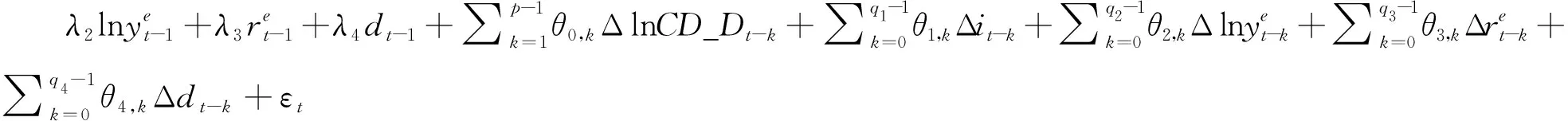
(8)

其中，Δ表示变量的一阶差分，p和qj分别为被解释变量和解释变量的水平变量滞后阶数，j=1，2，3，4。首先根据AIC或SC信息准则确定最优的ARDL(p，q1，q2，q3，q4)模型，然后采用F统计量来检验借贷资金需求与其影响变量之间是否存在长期协整关系，其中原假设为λ0=λ1=λ2=λ3=λ4=0，备择假设为λ0、λ1、λ2、λ3、λ4不全为0。如果F统计量大于临界值上限，则可拒绝原假设，说明变量之间存在协整关系；如果F统计量小于临界值下限，则不能拒绝原假设，说明变量之间不存在协整关系；若F值处于临界值上限与下限之间，则无法判断变量间是否存在协整关系。

变量间的协整关系确定后，下一步是估计借贷资金需求量与其影响变量之间的长期关系。借贷资金需求的ARDL长期模型可由下式表示：

(9)

然后可从(9)式得到变量之间的长期关系为：

(10)

在得到长期协整关系的基础上，笔者进一步建立误差修正模型，估计变量间的短期动态关系：

(11)

其中，η是调整系数，反映短期偏离向长期均衡的修正速度，若为负值，表示偏离均衡的误差得以修正；反之，则表示变量间不存在长期的动态调整关系。

类似的，可将借贷资金供给函数对应的实证模型(7)式转化为如下ARDL模型：

(12)

若边限检验表明变量间存在协整关系，则可建立借贷资金供给的ARDL长期模型：

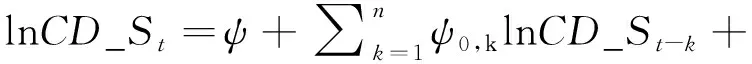
(13)

进而可从(13)式得到借贷资金供给的长期协整方程：

lnCD_St=ρ+ρ1it+ρ2lnyt+ρ3lnMt+ECt

(14)

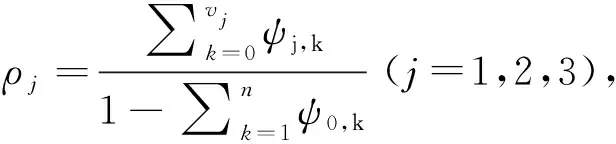
借贷资金供给函数的短期动态可由以下误差修正模型得出：

(15)

(二)指标选取与数据来源

考虑到数据的可得性，笔者选取1960—2017年的美国年度时间序列数据为样本进行实证分析。

对于借贷资金需求函数，被解释变量借贷资金需求量(CD_D)以境内非金融机构的借贷资金量代表。解释变量包括：第一，利率(i)，用优惠利率(Bank Prime Loan Rate)度量。优惠利率是美国银行向企业发放贷款的优惠利息率，它是一种基础性的贷款利息率。第二，预期产值(ye)，计算公式为预期产值=上期产值*(1+本期产值增长率预期值)，其中本期产值增长率预期值用前两期产值增长率的平均值来衡量。这种方法的理论基础在于：当人们无法得到更好的预测数据情况下，通常以过去产值的变动趋势预测未来产值变动。第三，预期利润率(re)，笔者用前两期利润率的平均值表示当期利润率的预期值。利润率用美国企业利润与国内总收入的比率表示。第四，财政收支(d)，采用财政收入与财政支出之差占GDP的百分比来衡量。财政收支变量为正值时表明存在财政盈余，财政收支变量为负值时表明存在财政赤字。

对于借贷资金供给函数，被解释变量借贷资金供给量(CD_S)用银行贷款作为代理变量。解释变量包括：第一，利息率(i)，与借贷资金需求函数中利息率变量的指标相同。第二，现期产值(y)，用现期国内生产总值表示。第三，货币供给(M)，用狭义货币供给量M1表示。

借贷资金需求量、借贷资金供给量、利息率和货币供给的数据来自美国联邦储备银行，产值和利润率的数据来自美国经济分析局，财政收支的数据来源于美国管理预算办公室。为了剔除物价水平变动的影响，笔者用CPI指数把借贷资金需求与供给、产值、货币供给量等名义变量缩减成实际值。

在下面的实证分析过程中，笔者主要采用EViews9软件，运用边限检验法来考察变量之间是否存在长期的协整关系。如果存在协整关系，则建立误差修正模型，进一步分析变量之间的短期动态调整情况。

(三)边限协整实证检验结果

1.单位根检验

ARDL边限检验要求变量为I(0)或I(1)或I(0)和I(1)的交叉型，而非I(2)或者更高阶单整。因此，在进行ARDL边限检验前，首先需要对各个变量进行单位根检验，以判断其平稳性。笔者采用ADF方法检验各变量的平稳性，检验过程中根据SIC准则确定各变量的滞后阶数，结果如表5所示。变量i、lny、lnye、lnM的水平序列在5%的显著水平上非平稳，一阶差分序列在5%的显著水平上平稳，所以这些变量是I(1)变量。变量lnCD_D、lnCD_S、re、d的水平序列在5%的显著水平上平稳，所以这些变量是I(0)变量。可看出各变量均为I(0)或I(1)变量，符合ARDL边限协整检验的要求。

2.边限协整检验

对设定的模型(8)和模型(12)进行边限协整检验，并根据AIC或SC准则选取最优的ARDL模型形式，结果可见表6。

ARDL边限检验结果表明，模型(8)的F统计量大于1%显著性水平的临界值上限，可认为借贷资金需求模型存在协整关系，即借贷资金需求与利率、预期产值、预期利润率和政府财政收支之间存在长期协整关系。而且确定模型形式为ARDL(4，1，3，0，4)，模型中含截距项。模型(12)的F统计量大于5%显著性水平的临界值上限，可判定借贷资金供给模型存在协整关系，即借贷资金供给与利率、现期产值、货币供给之间存在长期协整关系，而且确定模型形式为ARDL(2，0，1，0)，模型中含截距项。

3.借贷资金需求函数的估计结果

借贷资金需求量与各影响变量之间长期关系的估计结果如表7所示：第一，利息率的系数估计值显著为负，表明利率提高将抑制借贷资金需求量，这与前文构建的新利息率理论的分析一致。利息率提高一方面增加了居民借入资金的成本，从而抑制借贷资金的消费需求；另一方面增加了企业的投资成本，从而抑制借贷资金的投资需求，两方面的影响共同导致借贷资金需求量减少。第二，预期产值的回归系数值显著为正，表明预期产值在长期对借贷资金需求量有显著正向影响，这个结果符合新利息率理论的预期。当人们预期未来收入增加时，会增加消费支出，而且未来偿还贷款的能力增强，人们更愿意以消费信贷方式满足消费需求，两方面的影响将导致居民对借贷资金的消费需求量增加。第三，预期利润率的回归系数值显著为正，说明预期利润率提高将增加借贷资金需求量，与新利息率理论的分析一致。预期利润率越高，投资的收益越高，对借贷资金的投资需求量就越大。第四，财政收支的系数估计值显著为负，表明财政收支变量越小，财政赤字越大，借贷资金的政府需求就越大；反之财政收支变量越大，财政盈余越大，借贷资金的政府需求就越小，同样与新利息率理论的分析一致。

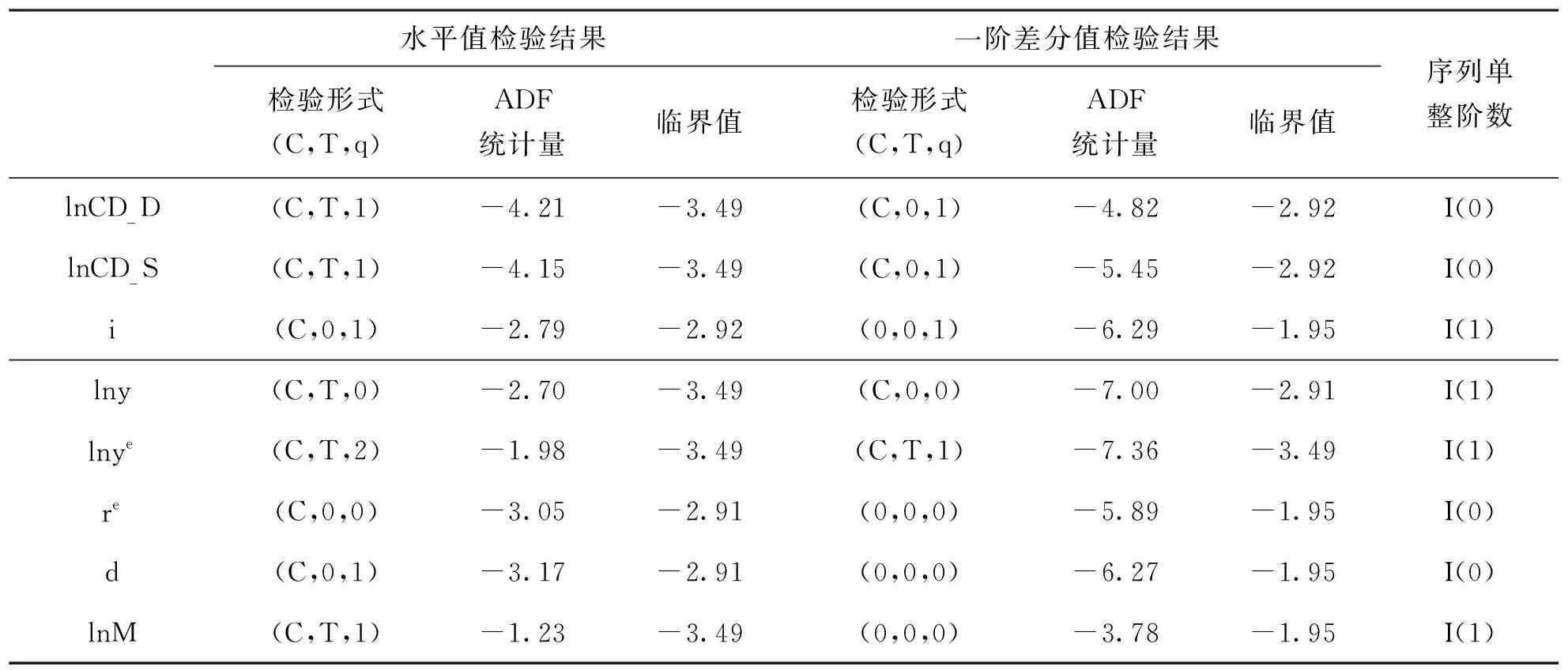
表5 各时间序列变量的单位根检验结果

表6 ARDL边限检验结果

表7 借贷资金需求函数的长期估计结果

根据表7，可以得到如下借贷资金需求函数：

(16)

笔者进一步采用误差修正模型对借贷资金需求量与各影响变量之间的短期动态关系进行分析，各变量系数估计结果如表8所示。借贷资金需求滞后项的系数显著为正，说明前三期借贷资金需求变动对本期借贷资金需求变化有正向影响。对于各影响因素变量，利息率在短期对借贷资金需求量会产生负向冲击。预期产值的当期系数和滞后一期系数显著为正，滞后二期的估计系数显著为负，但前者系数之和的绝对值大于后者系数的绝对值，因而预期产值对借贷资金需求量的净冲击为正。预期利润率在短期会正向冲击借贷资金需求量。财政收支当期和滞后一期的负向影响大于滞后二期和滞后三期的正向影响，而且滞后三期的正向影响不显著，所以财政收支对借贷资金需求的净效应仍为负。这些变量的影响方向都符合新利息率理论的预期，可见新利息率理论对现实经济具有相当的解释力。

误差修正项ECt-1的估计系数显著为负，符合反向修正机制，这也进一步证实了借贷资金需求与各影响变量之间存在协整关系。误差修正项的系数约为-0.3379。这表明，当各变量在短期偏离长期均衡时，那么33.79%的偏差能在下一期内消除。

为了确保上述估计的可靠性，需要对借贷资金需求函数对应的ARDL模型进行诊断检验，结果见表9。对于自相关的LM检验显示残差项不存在自相关，对于异方差的ARCH检验表明残差序列不存在异方差，对于模型形式设定的Ramsey RESET检验表明回归方程不存在设定误差，对于正态性的Bera-Jarque检验显示残差项服从正态分布。综上所述，借贷资金需求模型通过了诊断检验。

借贷资金需求函数的稳定性需要进一步通过稳定性检验加以确定。笔者利用CUSUM检验和CUSUMSQ检验来确认各影响变量长期系数和短期系数的稳定性。(9)软件Eviews9不能对ARDL模型进行CUSUM检验和CUSUMSQ检验，本文使用软件Eviews10进行了相关检验。图6显示借贷资金需求模型的CUSUM统计量和CUSUMSQ统计量都落在了5%显著性水平的置信边界之内，无法在5%的显著性水平下拒绝模型稳定的原假设，因而借贷资金需求模型表现出了良好的稳定性。

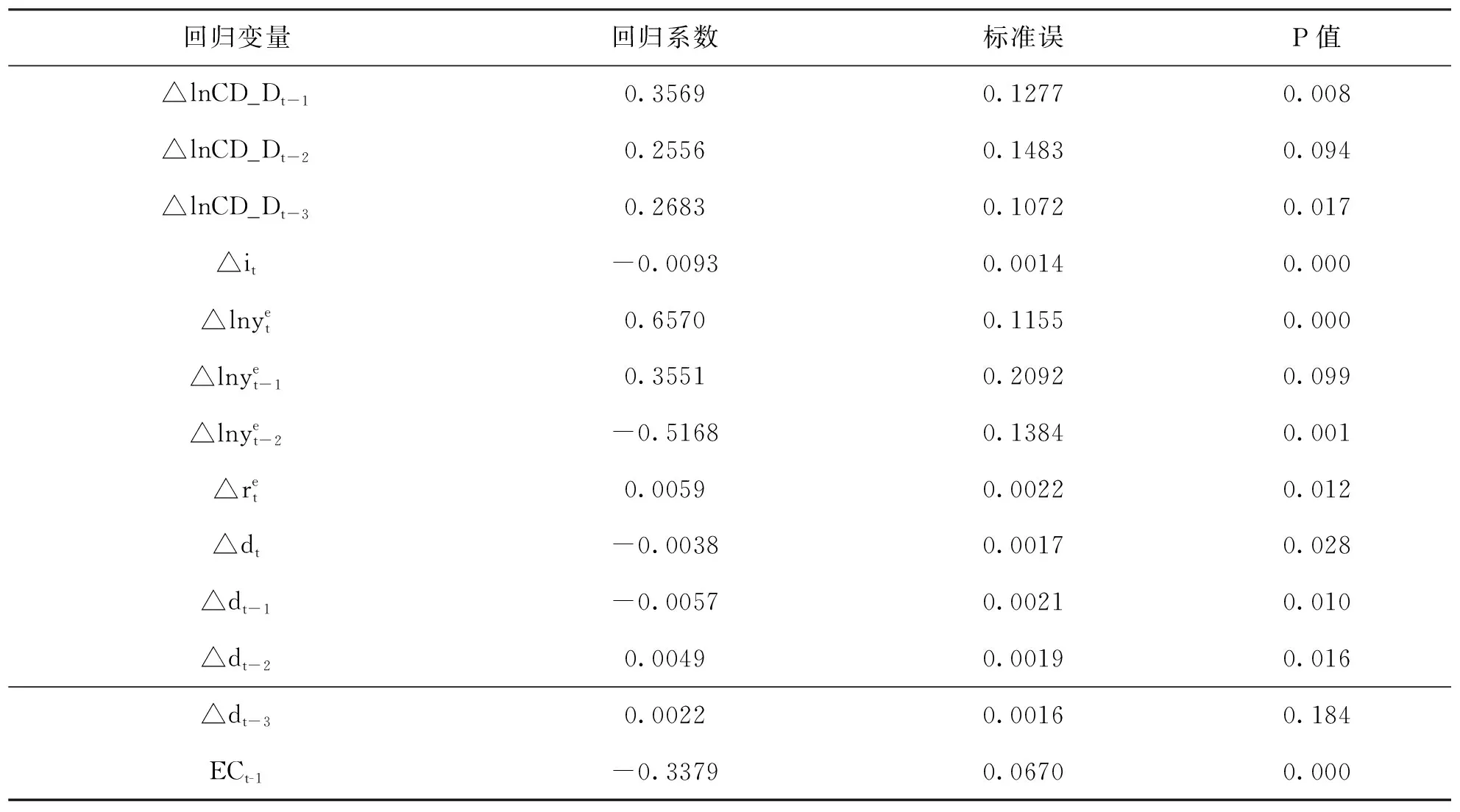
表8 借贷资金需求函数的短期估计结果

表9 借贷资金需求模型的诊断检验结果

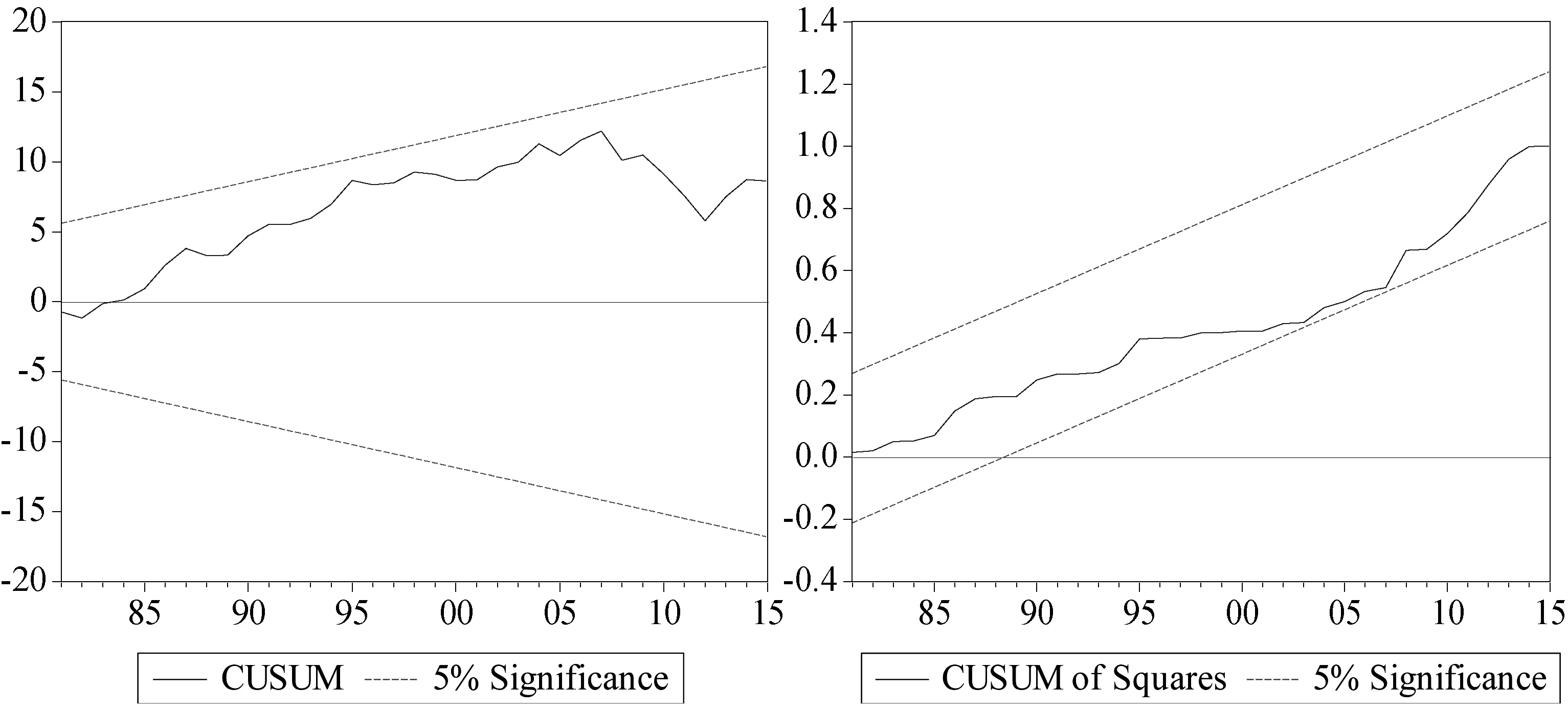
图6 借贷资金需求模型的稳定性检验

4.借贷资金供给函数的估计结果

借贷资金供给量与各影响变量之间长期关系的估计结果见表10。利率的系数估计值显著为正，表明利率提高将增加借贷资金供给，符合新利息理论的预期。利率提高增加了居民和企业的储蓄收益，居民和企业会增加储蓄，进而使得借贷资金供给量增加。现期产值的系数估计值显著为正，表明现期产值越大，借贷资金供给量就越大，与前文的理论分析一致。这是由于边际消费倾向小于1，现期产值越大，社会储蓄供给量就越大，借贷资金供给量也就越大。货币供给量的回归系数值显著为正，而且货币供给量增加1%，借贷资金供给量将增加0.71%。这不仅验证了货币供给与借贷资金供给之间的正相关关系，而且说明了货币供给增量并不完全构成借贷资金供给增量，只有一部分货币供给增量进入到借贷市场成为借贷资金的供给量。

根据表10，可以得到如下借贷资金供给函数：

lnCD_St=0.0452it+0.6009lnyt+0.7141lnMt-4.2623+ECt

(17)

表11给出了相应误差修正模型的估计结果。除了借贷资金供给本身滞后项的较大正向影响外，利率、现期产值和货币供给量在短期内都对借贷资金供给产生了正面冲击，各个影响因素变量的短期动态系数符号与长期协整方程系数符号一致，符合理论预期。误差修正项ECt-1的估计系数显著为负，意味着短期借贷资金供给量相对长期均衡的偏离将得到修正，也进一步确认了借贷资金供给量与各影响变量之间的协整关系。误差修正项的系数约为-0.2580，意味着上一期实际值和长期均衡值的偏离将有25.8%在下一期得到修正。

为了确保上述估计的可靠性，还需要对描述借贷资金供给量与其影响变量关系的ARDL模型进行诊断检验。表12显示，自相关检验、异方差检验、模型设定检验及正态性检验均不能拒绝原假设，表明模型不存在自相关和异方差，模型设定正确，残差服从正态分布，借贷资金供给模型通过了诊断检验。此外，还利用CUSUM检验和CUSUMSQ检验对借贷资金供给函数参数的稳定性进行分析。从图7可以看出，借贷资金供给模型的CUSUM、CUSUMSQ统计量均落在5%显著性水平下的临界区间内，说明借贷资金供给模型估计的参数是稳定的。

表10 借贷资金供给函数的长期估计结果

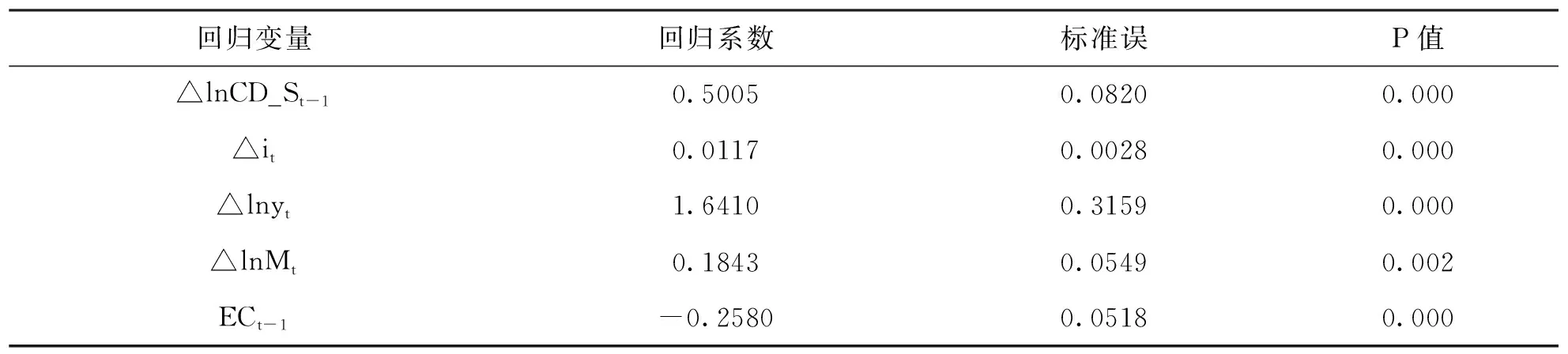
表11 借贷资金供给函数的短期估计结果

表12 借贷资金供给模型的诊断检验结果

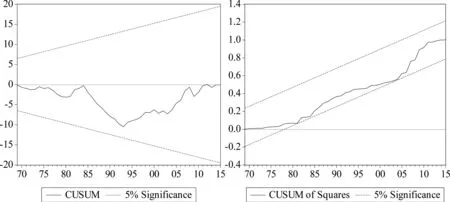
图7 借贷资金供给模型的稳定性检验

五、简短的结论

本文经过对魏克赛尔、凯恩斯、罗伯逊等的经典利息率理论的比较和分析，指出罗伯逊的利息率理论是比较完整的利息率理论。然而对美国和日本统计数据的分析表明，罗伯逊在对借贷资金需求的分析中强调了不重要的窖藏需求，忽略了在现实经济中对借贷资金具有重要影响的消费需求和政府需求。因此，本文在借贷资金需求的分析中删除了窖藏需求，增加了消费需求的因素并指出它是利息率和预期收入的函数，增加了政府需求的因素并指出它是财政赤字的函数，重新建构了新的利息率理论。对美国时间序列数据的计量分析表明，新建构的利息率理论符合现实经济情况，对现实经济借贷资金需求和供给的变化具有解释力。