寿阳区块高阶煤煤体结构及破裂压力测井解释方法

李松林，李忠城，王利娜，段 静，向 念

寿阳区块高阶煤煤体结构及破裂压力测井解释方法

李松林1，李忠城2，王利娜2，段 静2，向 念1

(1. 中海油能源发展股份有限公司工程技术分公司，天津 300452；2. 中联煤层气有限责任公司，北京 100022)

煤体结构及破裂压力直接影响煤层气开发的工程设计和产气效果，其中煤体结构评价方法较多，但针对寿阳区块高阶煤，地质强度因子(GSI)法效果最好，但其具有很强的地域适用性；煤层的非均质性极强，破裂压力预测效果并不理想。针对上述问题，通过引入取心率、连续心长等参数优化地质强度因子法，进而建立适用于本区的煤体结构定量评价方法，结果表明，其测井解释结果准确性达到86.3%。同时，在煤体结构评价的基础上，引入煤体破碎指数并建立煤层破裂压力预测公式，利用公式计算的破裂压力与实际相对误差2.5%~16.1%，平均误差8%。提出的煤体结构及破裂压力预测方法对沁水盆地高阶煤适用性较好，能够为煤层气勘探开发及压裂改造提供有力支撑。

测井曲线；煤体结构；地质强度因子；煤层破碎指数；破裂压力

随着煤层气勘探和开发进程日益加深，煤体结构及破裂压力因其直接影响煤层气的开发效果，其评价越来越受到重视，很多学者进行了相关研究，形成了多种理论及方法。煤体结构评价方法主要有采样标本描述法、钻井取心法、常规测井方法。常规测井方法具有连续性强、成本低、可靠性强的特点，广泛应用于煤体结构识别[1-3]。逐渐形成了聚类分析法、BP神经网络方法、主成分分析法、对应分析技术等定性评价方法[4-6]。近年来，部分学者通过引入地质强度因子GSI来探讨煤体结构精细描述的定量表达[7-9]，表现出较好的应用效果。煤层气开发需要储层改造，而破裂压力是煤层改造中的重要参数，很多学者进行了相关研究。杜国峰等[10]应用黄氏(黄荣樽)模型对地应力和破裂压力进行计算；李剑等[11]、倪小明等[12]开展了煤体结构在射孔优化及岩石力学方面的研究。一方面，不同地区受沉积、构造环境影响，煤储层非均质性强，煤体结构差异大，前人在他区开展的煤体结构评价很难直接套用到本区。另一方面，前人利用纵横波、密度等参数基于压实理论、摩尔库伦法则计算煤层破裂压力，但由于煤层超高的声波时差，其效果并不理想。

针对上述问题，有必要开展寿阳区块煤体结构评价及破裂压力预测方法研究。沁水盆地寿阳区块属于高煤阶煤层，基于已有研究基础，结合本区储层条件，笔者通过引入取心率、连续心长、破碎程度、煤体强度表征煤心煤体结构，优化地质强度因子GSI法后建立了适合本区的评价方法；而后在煤体结构评价的基础上，引入煤层破碎指数，建立煤层破碎指数与破裂压力关系，预测破裂压力，以期为煤层气开发过程中工程设计提供依据。

1 煤体结构评价

根据煤的碎裂程度、成因类型及结构特征，不同学者提出了不同的煤体结构划分方法[8,13-14]。目前，应用最广泛的煤体结构划分办法为GB/T 30050—2013《煤体结构分类》，将煤体结构划分为4类：原生结构、碎裂结构、碎粒结构和糜棱结构。寿阳区块属于沁水盆地高煤阶煤层，适用上述4类划分方法。

近年来，部分学者通过引入地质强度因子GSI来探讨煤体结构精细描述的定量表达[7-9]，表现出较好的应用效果。地质强度因子GSI(Geological Strength Index)是由E. Hoek等[15-17]在1995年建立的岩体分类方法中一种量化指标，可有效表征煤体结构。GSI值的确定主要取决于岩体结构的完整度、岩体结构面裂隙、节理的质量状况等(表1)。

表1 不同煤体结构的GSI估测值(李广生等[4]，2015)

在此基础上，本文结合煤层钻井及取心情况研究发现，煤体结构与取心率及连续心长存在一定相关性。一方面，由于煤体机械强度低，导致随着煤层破碎程度增加取心率降低；另一方面，连续心长越大煤层强度越高，煤体结构越好。因此，取心率及连续心长也可以作为煤体结构表征参数。

综合以上分析研究，确定寿阳区块煤体结构及GSI表征参数为取心率、连续心长、破碎程度和煤岩强度。表现为：原生结构为完整层状，取心率高，连续心长大，煤岩成块状；碎裂结构受到一定程度的破坏，取心率较高，煤样呈厘米级，团块、碎块状，可见外生裂隙；碎粒结构煤取心率较低，煤样呈粒级，煤体破碎较严重，煤体强度低；糜棱结构煤体受到严重破坏，取心率特低甚至取不到煤心，煤体呈粉末状、细小碎粒状或煤浆状。研究区取样结果如图1所示，煤样地质强度因子见表2。

图1 寿阳区块不同煤体结构煤心

煤体结构一般与伽马、密度、中子、声波、井径、电阻率等测井数据相关[18]。本文对上述参数研究发现，寿阳区块煤体结构仅与井径、伽马、密度以及电阻率关系较好(图2)，其测井曲线响应特征为：煤体破碎程度越高，钻井扩径越大，孔隙率越大，电阻率越低，煤体疏松，密度越小；煤体孔隙和裂隙越发育，单位体积内放射性物质含量降低，伽马越低。不同煤体结构测井响应参数值见表3。

通过上述测井曲线响应关系，应用Excel数据分析模块，借助多元线性回归建立GSI计算方法：

GSI=92.399 7–0.162 05×GR–1.458 88×(CALX+

CALY)/2+0.002 938×RD+7.888 8×DEN

2=0.648 5 (1)

式中：GSI为地质强度因子；GR为伽马，API；RD为电阻率，Ω·m；DEN为密度，g/cm3；CALX、CALY为双井径，cm。

通过上述方法对研究区煤层进行评价，如图3所示。从图中可以看出，利用测井参数计算得到的GSI值与煤心GSI值数据(绿色点)吻合度较高。对研究区16口取心井(共183个样本点)进行吻合度分析，煤体结构解释结果与煤心样品吻合率71.4%~93.2%，平均86.3%，结果见表4。

表2 寿阳区块煤样地质强度因子表征

图2 不同测井数据与地质强度因子交会图

表3 不同煤体结构测井参数响应值

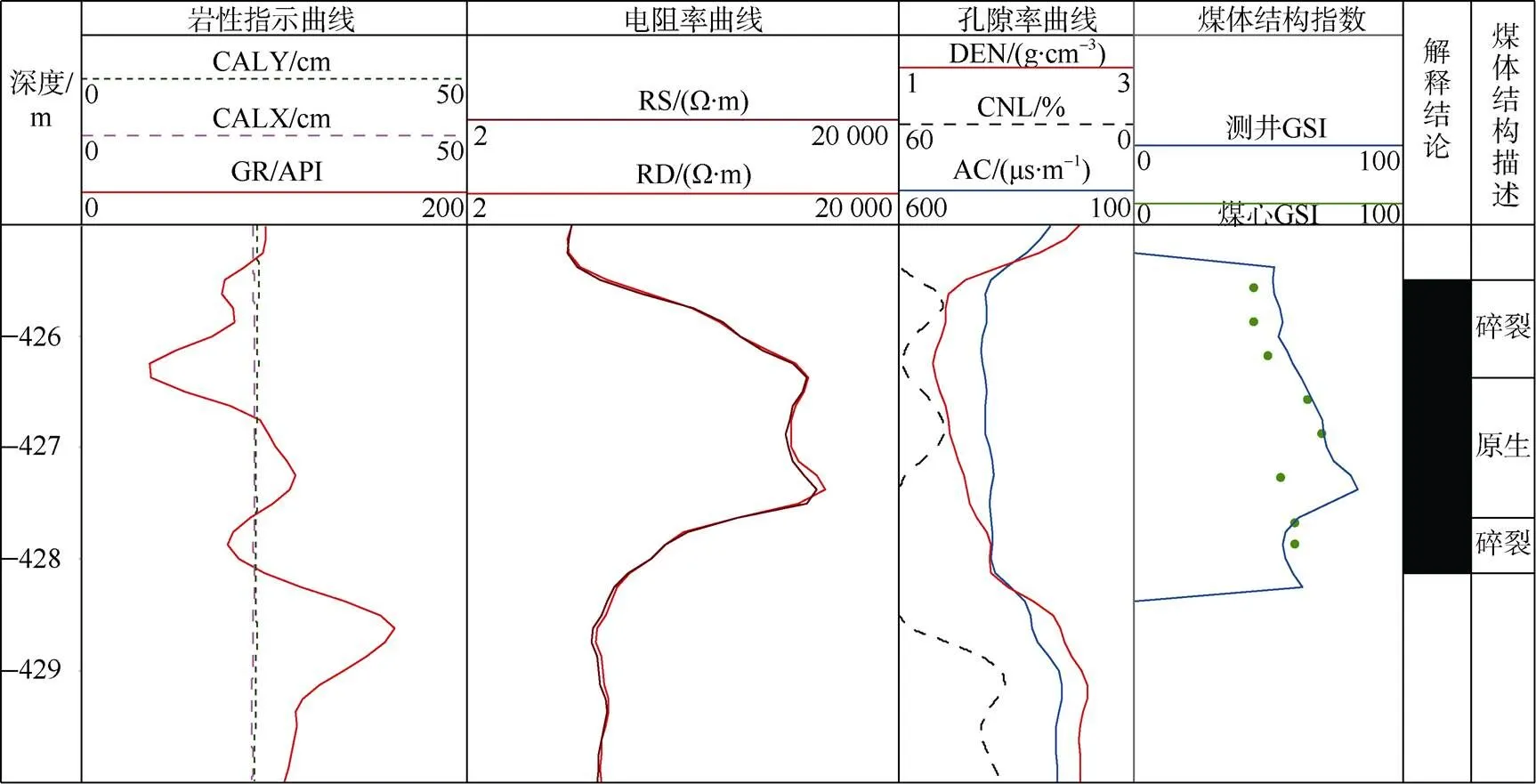
图3 测井曲线煤体结构解释与煤心结果对比

表4 测井资料煤体结构评价结果

2 煤体结构与破裂压力关系

根据测井曲线中纵波、横波及密度曲线，利用压实理论、摩尔库伦法则计算常规储层(砂泥岩、碳酸盐岩等)岩石力学参数效果较好。部分学者将该方法引入到煤层地应力、破裂压力计算中来[19-20]，但效果并不理想。其方法是先计算地层压力，垂向应力、最大最小水平主应力等岩石力学参数后，进而计算地层破裂压力[15-16]：

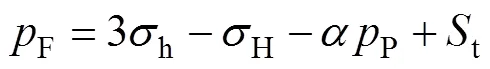
通常情况下，H=3h、将式(3)、式(4)代入式(2)，整理得到：

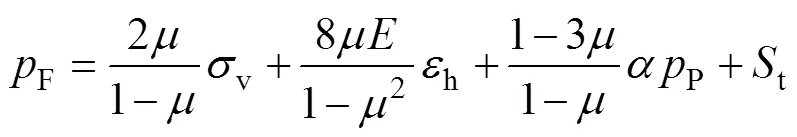
式中：F为破裂压力，MPa；v为垂向应力，MPa；H、h、w分别为最大、最小和水平主应力，MPa；为弹性模量，GPa；为泊松比；P为地层压力，MPa；H、h为构造应力系数；Δ、Δn分别为压实线声波时差和实测声波时差，μs/304.8 mm；t为抗张强度，MPa。

由式(5)可知，地层压力是声波时差函数，煤层本身超高声波时差(并非由孔隙和孔隙流体引起)导致煤层地层压力计算值过高。由式(3)、式(4)、式(6)可知，破裂压力与地层压力正相关，过高的地层压力会直接影响地应力和破裂压力的计算。因此，对于煤层这种特殊储层，测井岩石力学计算方法需要进一步改进。

本文通过研究分析现场压裂施工情况，结合前人研究[21-22]发现，煤体结构直接影响煤层破裂压力的大小，这为煤层破裂压力预测提供了一种新的途径。

A1井煤体结构为碎裂结构–糜棱结构，其破裂压力较高(32 MPa)，A2井煤体结构为原生结构–碎裂结构，其破裂压力较低(13 MPa)(破裂压力由图4中套压曲线读取。为统一不同深度、不同井的可对比性，将破裂压力转化为破裂压力梯度，进而可以系统地分析其与煤体结构之间的关系。

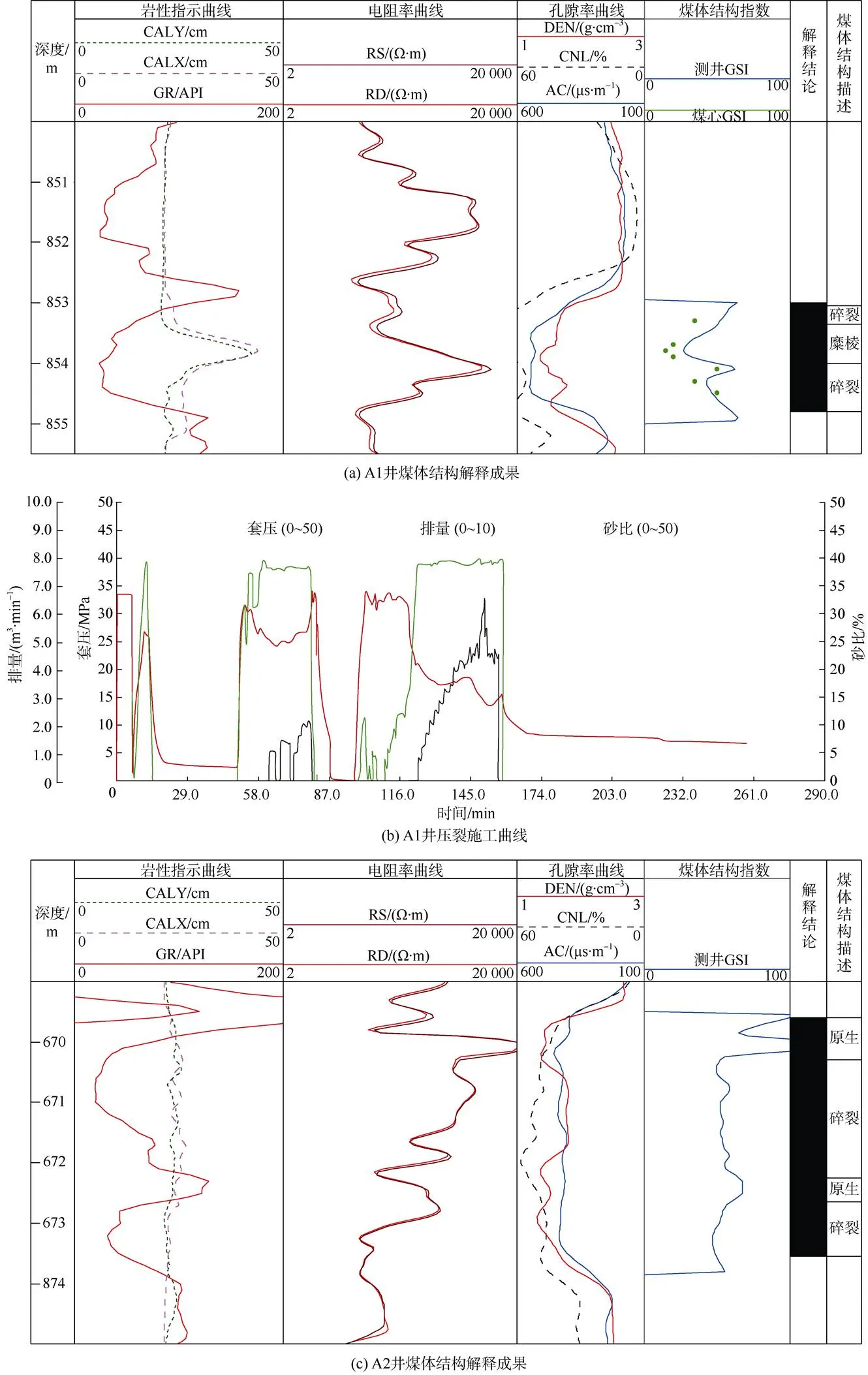
由图4发现，煤层含有糜棱及碎粒结构煤时(图4b)，对应的破裂压力均会升高。针对这一现象，建立煤层破碎指数：即糜棱结构及碎粒结构煤层厚度占煤层总厚度比，由于所有煤层本身均存在裂隙，所以煤层均存在一定破碎，故全≥5%。

=(m+b)/(7)

c=g×/100 (8)

式中：c为破裂压力，MPa；g为破裂压力梯度，MPa/hm；m、b分别为煤层中糜棱煤厚度和碎粒煤厚度，m；为煤层总厚度，m。

通过对该区已压裂井的破裂压力梯度与煤层破碎指数(表5，图5)进行分析研究，并利用图5中的拟合公式计算了13口参数井的破裂压力，计算结果与真实施工破裂压力的相对误差2.5%~16.1%，平均误差8%(表5)。由表中可以看出，基于煤体结构的煤层破裂压力预测方法效果较好。这种方法可有效解决同一地区、同一煤层不同井间、不同深度煤层的破裂压力梯度差异较大问题。

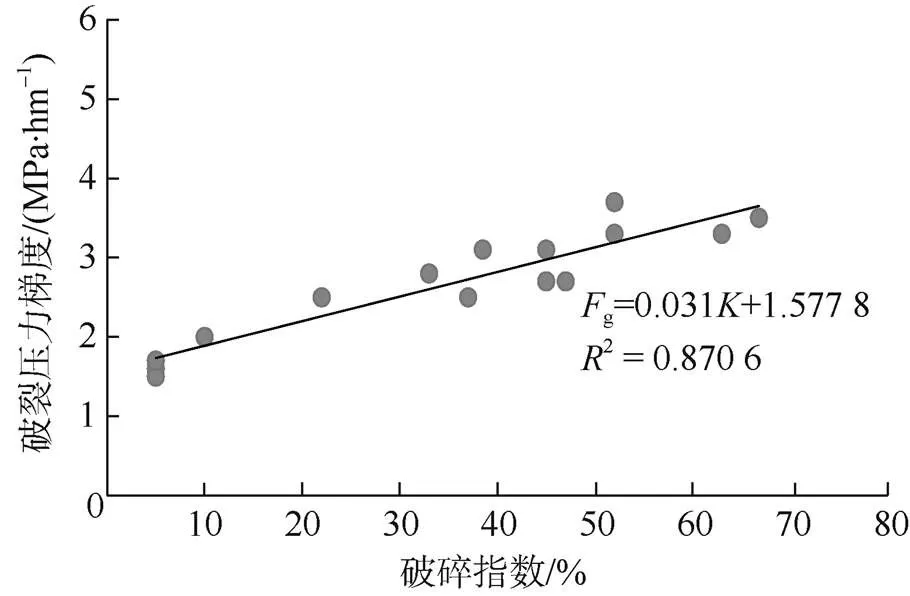
图5 破碎指数与破裂压力梯度关系

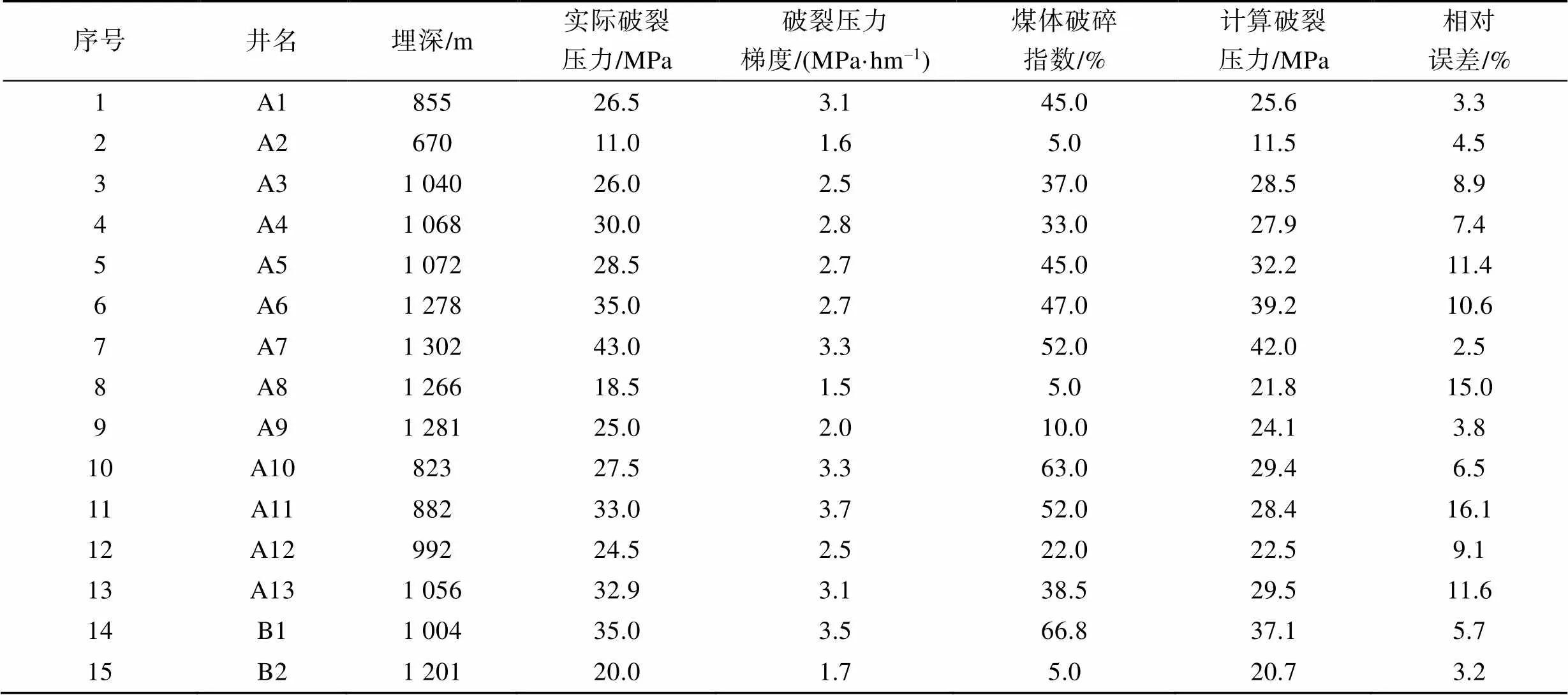
表5 煤体破碎指数与煤层破裂压力关系

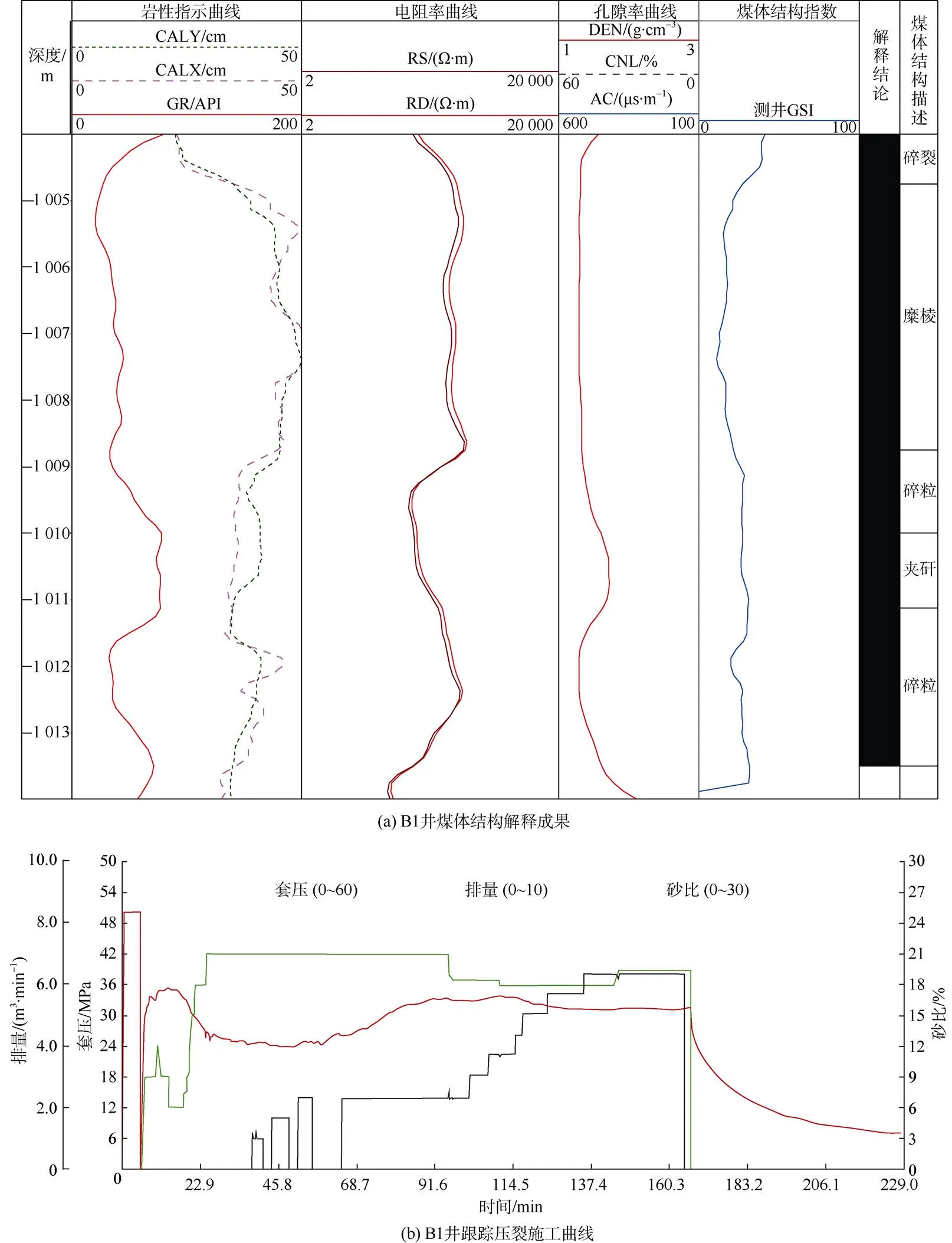
为进一步验证该方法的准确性，对研究区内2口待压裂井的煤层破裂压力进行预测。B1井：煤层埋深1 004 m，煤体结构差，煤层破碎指数=66.8%，预测破裂压力37.1 MPa；B2井：煤层埋深1 202 m，煤体结构好，破碎指数=5%，预测破裂压力20.7 MPa。跟踪2口井压裂施工情况，其真实施工破裂压力分别为35 MPa和20 MPa，与预测破裂压力误差较小(图6)。

利用煤体结构评价、煤层破裂压力预测结果，可有效为压裂射孔优选、压裂规模、造缝模拟、加砂规模等储层改造优化提供有力支撑[23-24]。

3 结论

a. 引入取心率、连续心长等参数用于表征煤体结构，并对地质强度因子GSI法进行优化，进而利用多元线性回归方法建立了适用于寿阳区块的煤体结构定量评价方法，测井解释符合率86.3%。

b. 在煤体结构评价的基础上，建立煤层破碎指数与破裂压力梯度关系法，预测破裂压力相对误差2.5%~16.1%，平均相对误差8%，为煤层破裂压力预测提供了新的途径。

c. 煤体结构评价及破裂压力预测方法可以为煤层气勘探开发及压裂施工优化提供有力支持。研究成果对沁水盆地高煤阶煤层适用性较好，其他区块及类似煤层有待进一步研究。

[1] 陈健杰，江林华，张玉贵，等. 不同煤体结构类型煤的导电性质研究[J]. 煤炭科学技术，2011，39(7)：90–93. CHEN Jianjie，JIANG Linhua，ZHANG Yugui，et al. Study on coal conductive properties of different coal structure[J]. Coal Science and Technology，2011，39(7)：90–93.

[2] 陈跃，汤达祯，许浩，等. 应用测井资料识别煤体结构及分层[J]. 煤田地质与勘探，2014，42(1)：19–23. CHEN Yue，TANG Dazhen，XU Hao，et al. Application of logging data in recognition of coal structure and stratification[J]. Coal Geology & Exploration，2014，42(1)：19–23.

[3] 倪小明，陈鹏，李广生，等. 恩村井田煤体结构与煤层气垂直井产能关系[J]. 天然气地球科学，2010，21(3)：508–215. NI Xiaoming，CHEN Peng，LI Guangsheng，et al. Relations between productivity of CBM vertical wells and coal structure in Encun mine field[J]. Natural Gas Geoscience，2010，21(3)：508–215.

[4] 李广生，孙明闯，史小卫，等. 基于地质强度因子的煤体结构精细描述[J]. 中州煤炭，2015(7)：121–124. LI Guangsheng，SUN Mingchuang，SHI Xiaowei，et al. Fine description of coal structure based on geological strength index[J]. Zhongzhou Coal，2015(7)：121–124.

[5] 马国栋，陈同俊，崔若飞. 测井曲线识别构造煤实例研究[J]. 地球物理学进展，2017，32(3)：1208–1216. MA Guodong，CHEN Tongjun，CUI Ruofei. Identification of tectonically deformed coal using well logs：A case study[J]. Progress in Geophysics，2017，32(3)：1208–1216.

[6] 侯月华，姚艳斌，杨延辉，等. 基于对应分析技术的煤体结构判别：以沁水盆地安泽区块为例[J]. 煤炭学报，2016，41(8)：2041–2049. HOU Yuehua，YAO Yanbin，YANG Yanhui，et al. Discriminate method of coal structure based on correspondence analysis technology：Acase study in the Anze area，Qinshui basin[J]. Journal of China Coal Society，2016，41(8)：2041–2049.

[7] 李广生，孙明闯，史小卫，等. 基于地质强度因子的煤体结构精细描述[J]. 中州煤炭，2015(7)：121–124. LI Guangsheng，SUN Mingchuang，SHI Xiaowei，et al. Fine description of coal structure based on geological strength index[J]. Zhongzhou Coal，2015(7)：121–124.

[8] 谢学恒，樊明珠. 基于测井响应的煤体结构定量判识方法[J]. 中国煤层气，2013，10(5)：27–29. XIE Xueheng，FAN Mingzhu. Quantitative identification of deformed coals based on logging response[J]. China Coalbed Methane，2013，10(5)：27–29.

[9] 陶传奇，王延斌，倪小明，等. 基于测井参数的煤体结构预测模型及空间展布规律[J]. 煤炭科学技术，2017，45(2)：173–177. TAO Chuanqi，WANG Yanbin，NI Xiaoming，et al. Prediction model of coalbody structure and spatial distribution law based on logging parameters[J]. Coal Science and Technology，2017，45(2)：173–177.

[10] 杜国峰，郭大立，薛玲，等. 煤层地应力及破裂压力解释技术[J]. 大庆石油地质与开发，2014，33(6)：171–174. DU Guofeng，GUO Dali，XUE Ling，et al. Interpreting techniques of the terrestrial stress and fracture pressure for coal beds[J]. Petroleum Geology and Oilfield Development in Daqing，2014，33(6)：171–174.

[11] 李剑，刘琦，熊先钺，等. 渭北区块煤体结构测井评价及其在射孔段优化中的应用[J]. 煤田地质与勘探，2017，45(6)：54–59. LI Jian，LIU Qi，XIONG Xianyue，et al. Evaluation of coal structure by logging and its application in optimization of perforation section of coal reservoir in Weibei block[J]. Coal Geology & Exploration，2017，45(6)：54–59.

[12] 倪小明，苏现波，张小冬. 煤层气开发地质学[M]. 北京：化学工业出版社，2009NI Xiaoming，SU Xianbo，ZHANG Xiaodong. Coal bed methane development geology[M]. Beijing：Chemical Industry press，2009.

[13] 张许良，单菊萍，彭苏萍. 地质测井技术划分煤体结构探析[J]. 煤炭科学技术，2009，37(12)：88–92.ZHANG Xuliang，SHAN Juping，PENG Suping . Discussion and analysis on geological logging technology applied to divide coal mass structure[J]. Coal Science and Technology，2009，37(12)：88–92.

[14] 姜波，秦勇，叶诗忠，等. 用测井曲线划分煤体结构和预测煤储层渗透率[J]. 测井技术，2003(2)：140–143. JIANG Bo，QIN Yong，YE Shizhong，et al. Classification of coal structure and prediction of coal reservoir permeability by logging curve[J]. Logging Technology，2003(2)：140–143.

[15] HOEK E，BROWN E T. Practical estimates of rock mass strength[J]. Int. J. Rock Mech. Min. Sci.，1997，34(8)：1165–1186.

[16] BIENIAWSKI VON PREINL Z T，TAMAMES B C，FERNÁNDEZ J M G，et al. Rock mass excavability indicator：New way to selecting the optimum tunnel construction method[J]. Tunnelling and Underground Space Technology，2006，21：237.

[17] HOEK E. KAISER P. K. Support of underground excavation in hard rock[M]. Rotterdam：Balkema，1995：99–105.

[18] 魏迎春，闵洛平，常东亮，等. 基于测井资料的临汾区块煤体结构识别及其分布规律[J]. 中国煤炭，2017，44(4)：35–40. WEI Yingchun，MIN Luoping，CHANG Dongliang，et al. Structure identification and distribution regularities of coal in Linfen block based on well logging data[J]. China Coal，2017，44(4)：35–40.

[19] 邢力仁，柳迎红，王存武，等. 基于测井信息的煤层气地区地应力预测与综合评价[J]. 煤炭科学技术，2018，46(10)：216–221.XING Liren，LIU Yinghong，WANG Cunwu，et al. Geostress prediction and comprehensive evaluation based on logging information in coalbed methane block[J]. Coal Science and Technology，2018，46(10)：216–221.

[20] 陈勉. 页岩气储层水力裂缝转向扩展机制[J]. 中国石油大学学报(自然科学版)，2013，37(5)：88–94. CHEN Mian. Re-orientation and propagation of hydraulic fractures in shale gas reservoir[J]. Journal of China University of Petroleum(Edition of Natural Science)，2013，37(5)：88–94.

[21] 赵立强，刘飞，王佩珊，等. 复杂水力裂缝网络延伸规律研究进展[J]. 石油与天然气地质，2014，35(4)：562–569. ZHAO Liqiang，LIU Fei，WANG Peishan，et al. A review of creation and propagation of complex hydraulic fracture network[J]. Oil & Gas Geology，2014，35(4)：562–569.

[22] 贾奇峰，倪小明，赵永超，等. 不同煤体结构煤的水力压裂裂缝延伸规律[J]. 煤田地质与勘探，2019，47(2)：51–57. JIA Qifeng，NI Xiaoming，ZHAO Yongchao，et al. Fracture extension law of hydraulic fracture in coal with different structure[J]. Coal Geology & Exploration，2019，47(2)：51–57.

[23] 严成增，郑宏，孙冠华，等. 基于FDEM–Flow研究地应力对水力压裂的影响[J]. 岩土力学，2016，37(1)：237–246. YAN Chengzeng，ZHENG Hong，SUN Guanhua，et al. Effect of in-situ stress on hydraulic fracturing based on FDEM-Flow[J]. Rock and Soil Mechanics，2016，37(1)：237–246.

[24] 郭红玉，苏现波，夏大平，等. 煤储层渗透率与地质强度指标的关系研究及意义[J]. 煤炭学报，2010，35(8)：1319–1322. GUO Hongyu，SU Xianbo，XIA Daping，et al. Relationship of the permeability and geological strength index(GSI) of coal reservoir and its significance[J]. Journal of China Coal Society，2010，35(8)：1319–1322.

High rank coal structure and log interpretation method of fracture pressure in Shouyang block

LI Songlin1, LI Zhongcheng2, WANG Lina2, DUAN Jing2, XIANG Nian1

(1. CNOOC Energy Technology-Drilling & Production Co., Tianjin 300452, China; 2. China United Coalbed Methane Corporation, Beijing 100022, China)

Coal structure and fracture pressure directly affect the engineering design and gas production effect of coalbed methane development. There are many evaluation methods of coal body structure, for the high rank coal in Shouyang block, the geological intensity factor(GSI) method has the best effect, but it has strong regional applicability; The heterogeneity of coal seam is very strong, and the prediction effect of fracture pressure is not ideal. In view of the above problems, the geological intensity factor method is optimized by introducing parameters such as coring rate and continuous coring length, and then a quantitative evaluation method for coal structure in this area is established. The results show that the accuracy of logging interpretation is 86.3%. At the same time, based on the evaluation of coal structure, the coal fragmentation index is introduced and the prediction formula of coal seam fracture pressure is established. The relative error between the calculated fracture pressure and the actual value is 2.5%-16.1%, and the average error is 8%. The prediction method of coal structure and fracture pressure is suitable for high rank coal in Qinshui basin, and it can provide strong support for CBM exploration, development and fracturing.

logging curve; coal structure; geological intensity factor; coalbed crushing index; fracture pressure

请听作者语音介绍创新技术成果等信息，欢迎与作者进行交流

P618.11；TE377

A

10.3969/j.issn.1001-1986.2020.06.020

1001-1986(2020)06-0146-09

2020-07-15；

2020-10-15

国家科技重大专项项目(2017ZX05064)

National Science and Technology Major Project(2017ZX05064)

李松林，1986年生，男，天津市人，硕士，工程师，从事测井处理解释及研究工作. E-mail：lisl4@cnooc.com.cn

李松林，李忠城，王利娜，等. 寿阳区块高阶煤煤体结构及破裂压力测井解释方法[J]. 煤田地质与勘探，2020，48(6)：146–154.

LI Songlin，LI Zhongcheng，WANG Lina，et al. High rank coal structure and log interpretation method of fracture pressure in Shouyang block[J]. Coal Geology & Exploration，2020，48(6)：146–154.

(责任编辑 范章群)