矿山边坡地表变形的PSO-ELM预测模型

2021-01-30宁永香崔希民

煤田地质与勘探 2020年6期

宁永香，崔希民

宁永香1，崔希民2

(1. 山西工程技术学院地质与环境工程系，山西阳泉 045000；2. 中国矿业大学(北京) 地球科学与测绘工程学院，北京 100083)

为提高矿山边坡地表变形预测模型的精度，从矿山边坡地表变形影响因素角度考虑，建立了基于粒子群优化(PSO)极限学习机(ELM)的矿山边坡地表变形预测模型。结合经典的粒子群优化算法和极限学习机方法，提出矿山边坡地表变形影响因素同地表变形数值之间的耦合关系；采用中煤平朔安家岭露天矿区矿山边坡地表变形及影响变形因素的采集数据，应用ELM建立预测模型，并应用PSO对ELM预测模型的输入层与隐含层的连接权值、隐含层阈值进行优化，以提高其预测精度。研究表明，经过PSO的优化，将预测模型的最大相对误差(4.705×10–8)、均方误差(6.243×10–5)及均方根误差(0.008)等预测误差参数分别降低到1.516×10–8，1.158×10–5和0.003，说明PSO-ELM预测模型具有更高的预测精度，该预测模型可在后续研究中进一步应用于矿山边坡地表变形预测中，以期提升矿山生产安全。

矿山边坡；变形监测；粒子群算法；极限学习机；预测模型

近年来，随着露天矿山开采技术和开采装备的不断发展进步，开采深度不断加大，随之在露天矿区边坡区域也形成了很多高陡边坡，对矿区安全生产及人员安全造成了严重的安全隐患[1]。虽然地表变形监测技术发展迅速，监测精度和效率越来越高，但由于灾害具有突发性和随机性，导致无法对变形以及灾害进行有效预测和预警[2]。因此，考虑矿区多种变形影响因素数据的地表变形预测建模就显得尤为关键和重要，也逐渐成为矿山安全生产的重要保障[3]。

目前，变形预测模型主要有：时间序列模型[4]、BP神经网络[5]、灰色预测模型[6-7]、支持向量机[8-9]以及极限学习机[10-11]等方法。然而，如果采用时间序列模型，其误差相对较大，难以达到准确预测的目标。BP神经网络利用误差反向传播算法训练网络，通过选择适当的网络模型结构以及神经元个数来逼近非线性函数，能够良好的应用于矿山边坡形变预测问题，但其受网络结构和样本的影响较大，且易于陷入局部最小值，随着样本量的增加，训练时间成本也随之大幅度增加，限制了其性能的发挥[12]。灰色模型应用少量已知信息样本来预测未知样本，具有运算方便，原理简单等优势[13]。支持向量机应用核函数的小样本统计理论，有效避免了陷入局部最优值的问题，具有结构简单、稳定性强、泛化能力强等优势，但该算法对大规模训练样本难以实施，且其对参数和核函数选择较敏感，致使预测模型的稳定性较差[14]。极限学习机(Extreme Learning Machine, ELM)，随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，且在训练过程中无需过多设置初始参数，只需设置隐含层神经元的个数，与传统算法相比，ELM方法具有学习速度快、泛化性能好等优势[15]。但ELM方法依然存在输入层与隐含层的连接权值、隐含层阈值的优化问题，需选取适合的算法对其网络结构进行优化。

目前，用于优化变形预测模型网络结构的优化算法主要有：遗传算法[16]，差分进化算法[17]，粒子群算法[18]等。它们都属于进化算法的分支，很多学者对这些算法进行了研究，其中，差分进化算法性能最优，且算法比较稳定，反复运算均能收敛到同一个解；粒子群算法收敛速度次之，但算法不稳定，最终收敛结果容易受参数大小和初始种群的影响；遗传算法收敛速度相对较慢，但在处理噪声问题方面有很大优势。另外，在参数设置方面，差分进化算法主要有2个参数需调整，而遗传算法和粒子群算法仅需调整一个参数。因此，综合考虑其优化性能，最终选择粒子群优化(Particle Swarm Optimization, PSO)对预测模型的参数进行优化调整。

因此，笔者结合经典的粒子群优化算法和极限学习机方法，从矿山边坡地表变形影响因素和地表变形数值角度对预测模型进行实验设计，提出应用粒子群算法优化矿山边坡地表变形预测模型，分析了各类边坡地表变形的影响因素与机理，并将模型应用于中煤平朔安家岭露天矿区的边坡地表变形验证和预测，以期为矿山边坡地表变形预测提供一种新思路和新模型。

1 预测原理与方法

1.1 极限学习机基本原理

极限学习机是由南洋理工大学的Huang Guangbin等[19]在2006年提出的一种进化神经网络方法，该方法可以避免BP神经网络等传统人工智能方法存在的训练速度慢、易陷入局部极小值等缺陷。ELM输入层和隐含层的连接权值、隐含层的阈值可随机设定，且设定完成后无需再调整；隐含层和输出层之间的连接权值不需迭代调整，而是通过解方程组方式一次性确定，以上2个特点极大地提高了其预测性能。ELM的数学模型[20]为：

=(1)

式中：为网络隐含层节点的输出矩阵；为网络连接隐含层神经元和输出节点的权重矩阵；为网络目标期望输出矩阵。

ELM的训练目标是寻找模型的最优权值组合=(,,)[21]，使得下式成立：

min()=min║–║ (2)

式中：和分别为隐含层节点的输入权值和隐含层的偏置。在ELM算法中，一旦输入和，隐含层的输出矩阵就会被唯一确定。训练单隐层神经网络可转化为求解线性系统式(1)，且输出权重矩阵可以被确定。

ELM的训练过程即为求解式(1)的过程，其最小二乘解[22]为：

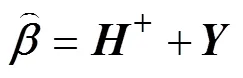
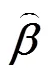
=(4)

1.2 基于PSO改进的ELM

传统的ELM存在权值、阈值随机性和网络参数不确定等问题，在处理大数据时效率较低，且存在过拟合现象，影响预测模型的效能。为此，引入PSO对ELM的权重和阈值等参数进行优化[20]，从而最大限度地发挥预测模型的预测效能。该模型优化流程主要包含以下几个重要步骤[21]：

①初始化粒子群体，设置PSO 相关参数，种群中粒子由输入权值和隐含层阈值构成，粒子长度计算公式为=(+1), 其中，为隐含层节点个数；为输入层神经元个数。

②将每个粒子对应的随机输入权值和阈值代入ELM算法中，得到输出权值矩阵的预测值，将训练样本计算出初始化种群每个粒子的均方根误差作为粒子适应度数值，比较当前粒子适应度数值与个体最优适应度数值，根据适应度较大值更新个体极值及全局极值。

③在迭代过程中更新粒子的速度和位置，当达到最大迭代次数或最佳适应度值时，停止寻优迭代过程。

④执行以上步骤得到最优输入权值和隐含层阈值，计算输出权值矩阵，得到最终预测结果。

1.3 边坡地表变形的影响因素与机理分析

1.3.1 降雨

在气象因素中，降雨能够显著影响矿山边坡形变程度。一方面，地表径流是冲刷矿山边坡的主要外力因素，地表雨水冲刷侵蚀着边坡坡面和坡脚，并且形成地表径流；另一方面，雨水渗透将会增加孔隙水压力，使土壤的黏结力和阻尼力降低[23]。因此，降雨是诱发矿山边坡滑坡发生的主要因素之一。图1为降雨对边坡变形的影响机理。

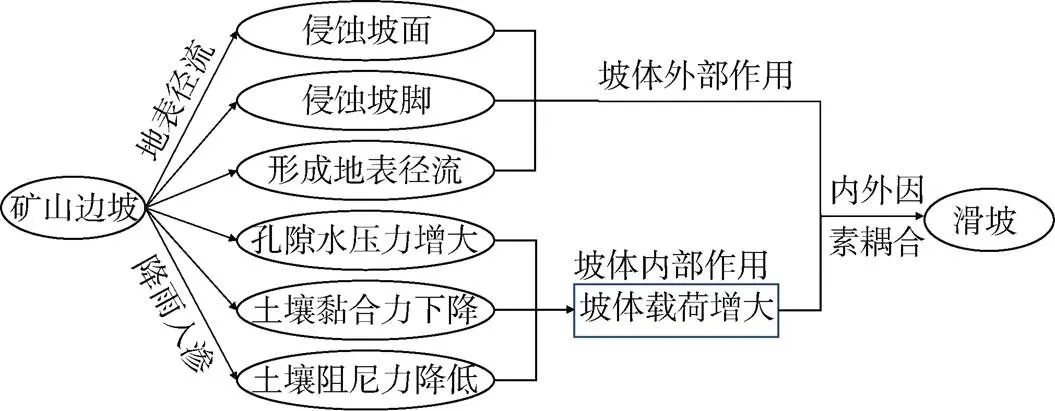
图1 降雨对边坡滑坡影响机理

1.3.2 温度

矿山边坡岩体外界的温度变化，会导致岩体发生膨胀或收缩现象，但由于岩体内外层温度的不同，其膨胀量和收缩量也会不同，因此，会导致岩体在孔隙率和黏结强度两方面发生变化。当大气温度高于边坡岩体温度时, 岩体吸热膨胀，孔隙率增加，最明显的特征是岩石破碎强度和弹性模量降低，导致抗压强度和抗变形强度的降低；当大气温度低于岩体温度时, 岩体放热收缩，黏结强度降低，最明显的特征是断裂伸长率下降和剥离强度降低，导致抗弯强度和抗张力的降低，从而加速地表变形乃至滑坡灾害的发生[23]。图2为温度对边坡滑坡的影响机理。

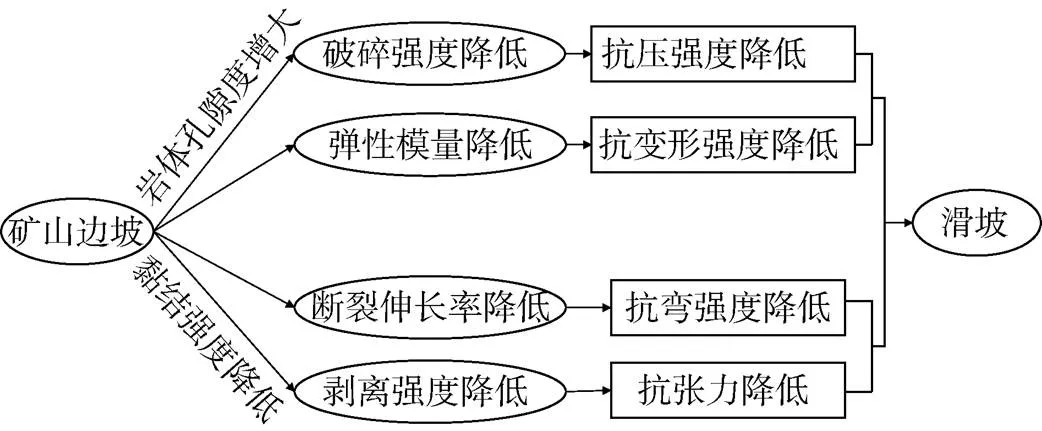
图2 温度对边坡滑坡的影响机理

1.3.3 开采活动

开采活动对边坡稳定性的影响主要包括以下3方面：增大边坡岩体本身的应力变化量；导致上覆平衡体滑移力增大，并作用在边坡体上，加大边坡岩体的变形与破坏程度；导致部分岩体抗载荷能力下降，加速边坡体破坏过程，从而影响边坡稳定性[24]。

除以上3个影响因素外，大气压强和相对湿度等同样对矿山边坡地表形变有着重要的影响，在本文中，以上信息均被用于矿山边坡地表形变预测研究中。

1.4 PSO-ELM形变预测方法

基于上述各形变影响因素数据，利用所建PSO-ELM预测模型来预测矿山边坡的地表形变。预测模型的输入为：矿山监测区域温度、大气压强、降雨量、相对湿度和开采记录。由于风速和风向的强随机扰动性，它们没有被选择作为输入变量。预测模型的输出是形变监测数据中某监测点的东坐标数据，北坐标数据和高程坐标数据。图3为PSO-ELM预测模型的变形预测过程。

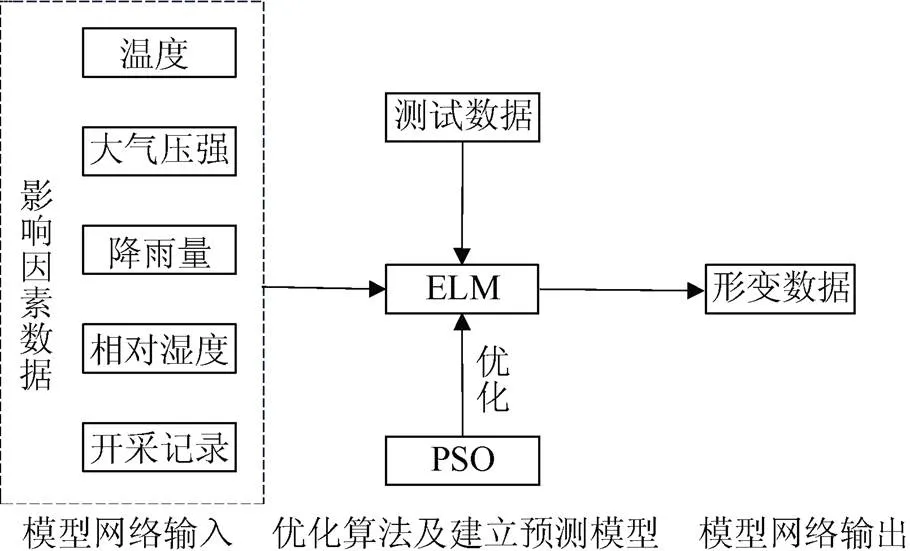
图3 PSO-ELM形变预测模型流程

2 矿区概况及实验数据采集

2.1 矿区概况

安家岭露天煤矿位于山西省朔州市平鲁区，总面积约28 km2，隶属于平朔矿区，是中煤平朔煤业有限责任公司下属的三大露天煤矿之一(图4)。该矿区属于温带半干旱大陆性季风气候区，春季冬季干旱少雨、寒冷、多风，夏季秋季降水集中、温凉少风，是矿山边坡变形灾害及地质灾害高发时期。平朔矿区年均降水量为428.2~449.0 mm，全年75%的降水量主要集中在7—9月。平朔矿区年平均气温为4.8~7.8℃，日温差较大，为18~25℃。

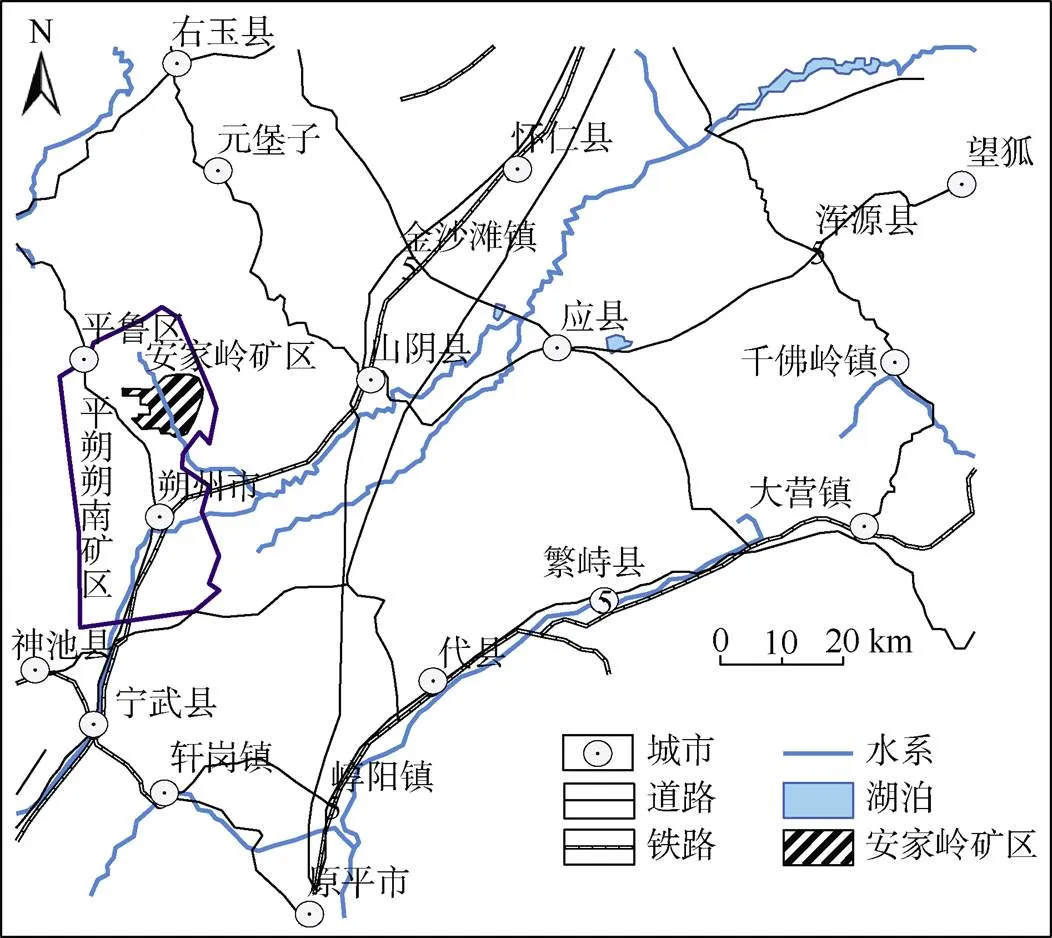
图4 安家岭矿区交通位置

安家岭北帮边坡地表部分的粉土层因具有大孔隙特征，部分降雨渗入后形成相对含水层，其渗透系数为(1.2~2.0)×10–5m/s，边坡坡面未见出水点。北端帮基岩节理裂隙发育，有若干出水点，其中4号煤层较为严重，表明基岩中仍含水，但从钻孔的静止水位来看，其水位在4号煤层底板，水位较低，说明岩体中含水量很少。

研究区域属于山西黄土高原朔平台地的低山丘陵，全区多为黄土覆盖，区内黄土台地曾受强烈的侵蚀切割作用，形成梁、垣、峁等黄土高原地貌景观。沟谷发育，呈“V”字形，切割深度40~70 m。区内地形基本呈北高南低趋势，中部高，两边低。

矿区内主要揭露地层为古生界石炭系、二叠系和新生界新近系和第四系。安家岭露天矿受控于区域构造影响，整体表现为倾向NE的平缓单斜构造，地层倾角为2°~10°，局部发育小型褶曲。矿区南部陷落柱较发育，陷落柱整体倾向SE，倾角变化大，最大可达52°。

鉴于煤矿内芦子沟背斜和安家岭逆断层主要影响煤矿南帮的采煤活动及边坡变形，对北帮影响较小，因此，在后续短期预测分析中主要考虑气象诱发因素的影响作用，未考虑地层岩性、地质构造及工程地质特征等因素。

2.2 实验数据采集

数据采集实验于2019年6月5日到2019年9月5日在中煤平朔安家岭露天矿展开，在此期间，该矿区北帮边坡监测区域由于降雨因素发生一起较明显的变形坍塌事故。该露天煤矿位于山西省北部，为掌握矿区边坡地表变形现状及趋势，应用SSR型地基干涉雷达对该研究区域边坡地表开展持续变形监测实验，变形影响因素监测数据和形变监测数据分别由Vantage Pro2型全自动气象站和SSR地基干涉雷达采集获取。

变形影响因素数据包括：矿山边坡监测区域温度，大气压强，相对湿度，累计降雨量，相对湿度和折射率。

形变监测数据包括：监测区域某点的东坐标、北坐标及高程坐标。

共计收集连续监测数据集150组，利用以上采集获取的监测数据，建立预测模型，从而预测矿山边坡地表变形数值，可初步掌握获取露天矿边坡地表变形和影响因素的非线性关系。

3 变形预测分析

3.1 模型学习参数

150组连续监测数据集的100组用于训练预测模型网络，50组用于测试和验证已训练好的预测模型网络。

经过经验公式及多次实验测试，最终确定该预测模型的学习参数设置见表1。

表1 预测模型学习参数设置

3.2 变形预测效果分析

为验证所建模型的预测精度，采用未经优化的ELM和PSO-ELM预测数值与实测数据进行对比分析。

图5为预测曲线与ELM输出曲线及PSO-ELM输出曲线的对比图。由图5可以看出，ELM及PSO-ELM输出曲线与预测输出曲线的总体趋势较为相似，且相较于ELM预测曲线，PSO-ELM预测曲线与实测数据曲线更加吻合，说明PSO对ELM起到较好的优化作用，使输出结果能够更好地对矿区边坡的三维变形进行预测。

图5 各种预测模型预测数值对比曲线

图6为ELM模型和PSO-ELM模型的输出误差对比曲线，可以直观地看出ELM预测模型误差变化区间较大，PSO-ELM预测模型的误差集中于“0”附近变化，结果反映出PSO-ELM模型的预测精度普遍优于ELM模型，能够体现出PSO对ELM模型的优化作用和效果。

图6 预测模型输出误差对比曲线

对ELM预测模型和PSO-ELM预测模型的预测精度从最大相对误差、均方误差以及均方根误差等预测精度评价参数角度进行了对比和分析(表2)，从表2可以看出，PSO-ELM预测模型的预测精度高于ELM预测模型，表明PSO-ELM预测模型具有更好的预测性能。

适应度值是预测模型目标函数值质量评价指标之一。用适应度值来评判目标函数值的质量，即判断模型预测结果是否达到预期设定的预测精度等既定预测目标。从图7可以看出，适应度数值随着进化代数的增加呈现明显的递减。在进化的前半段，适应度数值下降较快；在进化的后半段，适应度数值下降较慢，最终适应度数值为0.955 38，其数值接近于“0”，说明PSO-ELM预测模型是有效的。

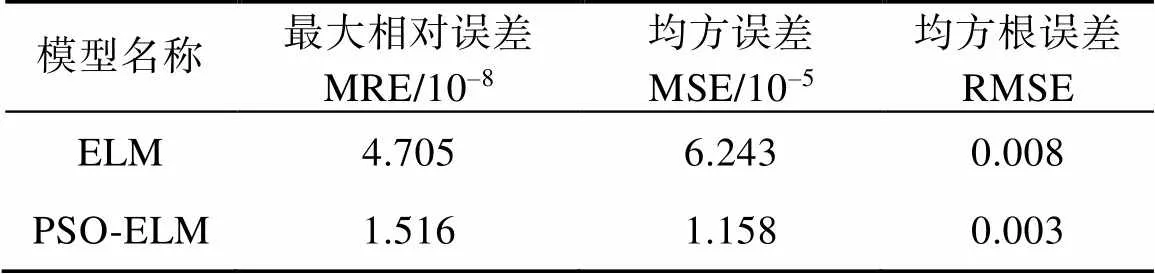
表2 ELM模型和PSO-ELM模型的预测精度对比

图7 PSO-ELM预测模型适应度值曲线

4 结论

a. ELM预测模型和PSO-ELM预测模型在露天矿边坡地表变形预测中可行，均可以采用变形影响因素数据较好地完成预测工作，实现露天矿边坡的变形灾害监测预警。

b. 应用PSO对ELM预测模型的输入层与隐含层的连接权值、隐含层阈值进行优化，可显著提高ELM预测模型的预测精度。

c. 根据实际情况，本文重点分析气象等外界诱发因素对边坡地表变形的影响；未考虑地层岩性、构造及岩土工程地质特征等因素对边坡地表变形的作用，今后需对此进行深入研究。

[1] ZHANG Fei，YANG Tianhong，LI Lianchong，et al. Cooperative monitoring and numerical investigation on the stability of the south slope of the Fushun west open-pit mine[J]. Bulletin of Engineering Geology and the Environment，2019，78(4)：2409–2429.

[2] DU Sunwen，FENG Guorui，WANG Jianmin，et al. A new machine-learning prediction model for slope deformation of an open-pit mine：An evaluation of field data[J]. Energies，2019，12(7)：1–15.

[3] 胡波，谭涵. 基于ARIMA模型的边坡变形分析与预测[J]. 测绘通报，2019(6)：112–116. HU Bo，TAN Han. Slope deformation analysis and forecast based on ARIMA model[J]. Bulletin of Surveying and Mapping，2019(6)：112–116.

[4] 罗亦泳，姚宜斌，王亚. 基于MRVM的多输出边坡变形预测模型[J]. 大地测量与地球动力学，2017，37(12)：1239–1242. LUO Yiyong，YAO Yibin，WANG Ya. Multi output slope deformation model based on multi-output relevance vector machine[J]. Journal of Geodesy and Geodynamics，2017，37(12)：1239–1242.

[5] 张磊，刘小明，来兴平，等. 基于 BP 神经网络的急倾斜煤层耦合致裂方案优化[J]. 西安科技大学学报，2018，38(3)：367–374. ZHANG Lei，LIU Xiaoming，LAI Xingping，et al. Optimization of coupled fracturing scheme for steeply inclined coal seam based on BP neural network[J]. Journal of Xi’an University of Science and Technology，2018，38(3)：367–374.

[6] XU Huafeng，LIU Bin，FANG Zhigeng. New grey prediction model and its application in forecasting land subsidence in coal mine[J]. Natural Hazards，2014，71：1181–1194.

[7] 芦家欣，汤伏全，赵军仪，等．黄土矿区开采沉陷与地表损害研究述评[J]. 西安科技大学学报，2019，39(5)：859–866. LU Jiaxin，TANG Fuquan，ZHAO Junyi，et al． Review of study on mining subsidence and ground surface damage in loess mining area[J]. Journal of Xi’an University of Science and Technology，2019，39(5)：859–866.

[8] LI Jinchao，GAO Fei，LU Jiaguo，et al. Deformation monitoring and prediction for residential areas in the Panji mining area based on an InSAR time series analysis and the GM-SVR model[J]. Open Geosciences，2019，11(1)：738–749.

[9] 姜刚，康艳霞，杨志强，等. 灰色理论模型在矿区滑坡变形预测中的应用[J]. 煤田地质与勘探，2011，39(3)：49–51. JIANG Gang，KANG Yanxia，YANG Zhiqiang，et al. Application of gray model to landslide deformation forecast in mining areas[J]. Coal Geology & Exploration，2011，39(3)：49–51.

[10] SUI Lichun，MA Fei，CHEN Nan. Mining subsidence prediction by combining support vector machine regression and interferometric synthetic aperture radar data[J]. ISPRS International Journal of Geo-Information，2020，9：390.

[11] WANG Xin，CHEN Tongjun，XU Hui. Thickness distribution prediction for tectonically deformed coal with a deep belief network：A case study[J]. Energies，2020，13：1169.

[12] DU Sunwen，LI Yao. A novel deformation forecasting method utilizing comprehensive observation data[J]. Advances in Mechanical Engineering，2018，10(9)：1687814018796330.

[13] Nwachukwu A，JEONG H，PYRCZ M. Fast evaluation of well placements in heterogeneous reservoir models using machine learning[J]. Journal of Petroleum Science and Engineering，2018，163：463–475.

[14] Martins F F，VASCONCELOS G，MIRANDA T. Prediction of the mechanical properties of granites under tension using DM techniques[J]. Geomechanics and Engineering，2018，15(1)：631–643.

[15] 孙世国，苏振华，王杰，等. 滑坡变形组合预测方法的研究[J].工程地质学报，2016，24(6)：1041–1047. SUN Shiguo，SU Zhenhua，WANG Jie，et al. Research on the synthetical prediction method of landslip deformation[J]. Journal of Engineering Geology，2016，24(6)：1041–1047.

[16] 唐睿旋，晏鄂川，唐薇. 基于粗糙集和BP神经网络的滑坡易发性评价[J]. 煤田地质与勘探，2017，45(6)：129–138. TANG Ruixuan，YAN Echuan，TANG Wei. Landslide susceptibility evaluation based on rough set and back-propagation neural network[J]. Coal Geology & Exploration，2017，45(6)：129–138.

[17] 王云宏，王保利，段建华. 基于差分进化算法的微震定位[J].煤田地质与勘探，2019，47(1)：168–173. WANG Yunhong，WANG Baoli，DUAN Jianhua. Microseismic positioning method based on differential evolution algorithm[J]. Coal Geology & Exploration，2019，47(1)：168–173.

[18] 梅杰，李光伟，夏成城，等. 基于仿生原理的粒子群算法求解江安校区水动力弥散系数[J]. 煤田地质与勘探，2019，47(6)：98–102. MEI Jie，LI Guangwei，XIA Chengcheng，et al. Particle swarm optimization-based bionic principle for solving hydrodynamic dispersion coefficient in Jiang’an Campus[J]. Coal Geology & Exploration，2019，47(6)：98–102.

[19] HUANG Guangbin，ZHU Qinyu，SIEW C. Extreme learning machine：Theory and applications[J]. Neurocomputing，2006，70(1/2/3)：489–501.

[20] MA Junwei，LIU Xiao，NIU Xiaoxu，et al. Forecasting of landslide displacement using a probability-scheme combination ensemble prediction technique[J]. International Journal of Environmental Research and Public Health，2020，17(13)：4788.

[21] YU J，LEE M，MOON Y，et al. Prediction of electropulse-induced nonlinear temperature variation of Mg Alloy based on machine learning[J]. International Journal of Environmental Research and Public Health，2020，58(6)：413–422.

[22] CHEN Renpeng，ZHANG Pin，WU Huaina，et al. Prediction of shield tunneling-induced ground settlement using machine learning techniques[J]. Frontiers of Structural and Civil Engineering，2019，13(6)：1363–1378.

[23] TAO Zhigang，ZHU Chun，ZHENG Xiaohui，et al. Slope stability evaluation and monitoring of Tonglushan ancient copper mine relics[J]. Advances in Mechanical Engineering，2018，10(8)：1–16.

[24] LI Zhiqiang，XUE Yiguo，LI Shucai，et al. Deformation features and failure mechanism of steep rock slope under the mining activities and rainfall[J]. Journal of Mountain Science，2017，14(1)：31–45.

PSO-ELM prediction model for surface deformation of mine slope

NING Yongxiang1, CUI Ximin2

(1. Department of Geology and Environment, Shanxi Institute of Technology, Yangquan 045000, China; 2. College of Geoscience and Surveying Engineering, China University of Mining and Technology(Beijing), Beijing 100083, China)

In order to improve the model accuracy of slope surface deformation prediction data, the influence factors of surface deformation of mine slope was considered and the prediction model of the limit learning machine was established based on particle swarm optimization. Firstly, the mine slope surface deformation monitoring data and influencing factors data were used to establish the prediction model utilizing the classical particle swarm optimization algorithm and the limit learning machine method. Secondly, the surface deformation of the mine slope and its influencing factors were collected in Anjialing open-pit mining area. Particle swarm optimization(PSO) was applied to optimize the connection weight and threshold of the input layer and the hidden layer to improve the prediction accuracy of the model. Finally, through the optimization application of PSO, the maximum relative error(4.705×10–8), mean square error(6.243×10–5) and root-mean-square error(0.008) of the prediction model were reduced to 1.516×10–8, 1.158×10–5and 0.003 respectively. The experimental results showed that the proposed prediction model had higher prediction accuracy than other models, and it could be applied to the prediction of surface deformation of mine slope in the follow-up study, so as to improve the safety level of mine.

mine slope; deformation monitoring; particle swarm optimization; extreme learning machine; prediction model