船舶桨-轴系统双向流固耦合动力学建模方法研究
2021-01-29邹冬林焦春晓徐江海饶柱石
邹冬林,焦春晓,徐江海,塔 娜,饶柱石
(上海交通大学a.振动、冲击、噪声研究所;b.机械系统与振动国家重点实验室,上海200240)
0 引 言
船舶螺旋桨在水中工作时,由于船体艉部绕流、轴系或船体振动、海洋湍流等因素导致螺旋桨伴流场的不均匀性,从而不可避免地在桨叶上产生激励力。螺旋桨激励力通过轴系各轴承传递至船体进而引起船体振动并辐射低频噪声,从而降低船舶的舒适性。众所周知,低频噪声衰减慢,传播距离远,且难以控制。而由螺旋桨激励力激起的桨-轴系-艇体耦合振动产生的低频噪声除具备通常低频噪声的特点外,还具有其独特性——线谱和窄带谱结构特征极其明显(主要由轴频、叶频及其倍频激励桨叶、轴系及船体等结构共振频率激励导致)。针对这类低频噪声,降噪的关键是掌握其频谱结构特征(即线谱和窄带谱结构特征)的成因[1],从而有针对性地对不同的频谱特征采用不同的降噪方法。因为桨-轴系-船体系统与艉部不均匀伴流场构成一个复杂的流-固-声耦合系统,致使目前很难认识这类低频噪声的产生机理,使得当前的振动噪声治理技术难以有效应用,减振降噪的效果不明显。因此,掌握螺旋桨激励导致的桨-轴系-船体耦合系统产生的低频振动噪声机理进而加以控制,已经成为当前我国船舶减振降噪急需解决的关键问题之一。
从螺旋桨激励力引起的低频噪声的产生原因(前面已阐述)可以知道,这类低频噪声的频谱结构特征与螺旋桨激励力特性以及桨-轴系统动态特性均密切相关。因而对螺旋桨激励力特性以及桨-轴系统振动特性的研究有助于我们掌握这类低频噪声频谱结构特征的成因。尽管螺旋桨激励力特性以及桨-轴系统耦合振动特性是两个不同的研究内容,但是他们之间又是一个不可分割的整体。一方面,掌握螺旋桨激励力特性可为桨-轴系统振动响应计算提供准确的输入条件;另一方面,桨-轴系统耦合振动又将对螺旋桨激励力产生反馈影响。因此不应将螺旋桨激励力特性以及桨-轴系统动态特性割裂开来单独研究,而是需要从流体、螺旋桨及轴系三者间的耦合关系入手,从中阐明这些复杂耦合因素对桨-轴系统振动特性及螺旋桨激励力特性的影响规律,并最终揭示这类低频噪声中线谱和窄带谱结构特征的成因。总之,最关键的问题是要建立一个流体-桨-轴系统双向流固耦合动力学模型。
流体-桨-轴系统流固耦合动力学涉及流体动力学、螺旋桨动力学及轴系动力学等三方面的理论知识,研究过程非常复杂,因此,国内外直接对流体-桨-轴系统流固耦合振动研究的文献非常少。已有研究中,大多数把这一问题割裂为两个问题单独研究:流体-螺旋桨流固耦合动力学分析及桨-轴系统振动分析。对于第一个问题,通常将螺旋桨从桨毂处断开,忽略轴系的影响。国内外对这个问题作了大量研究:Jang 等[2]利用升力面理论结合有限元方法提出了考虑流固耦合效应的螺旋桨设计方法;Lee等[3]利用边界元理论(BEM)耦合有限元法(FEM)分析了复合材料螺旋桨在非均匀来流下的流固耦合特性,并将结果与基于商业软件的CFD-FEM(Star-CCM+/Abaqus)方法进行比较[4];类似地,Li等[5]也利用边界元耦合有限元方法计算了螺旋桨在非均匀来流下的流固耦合性能,重点讨论了螺旋桨湿模态的影响因素;Ghassemi 等[6]基于商业软件的CFD-FEM(ANSYS/CFX)方法计算了复合材料螺旋桨在均匀来流下的流固耦合力学性能;同样,Hong 等[7]也基于商业软件的CFD-FEM(ANSYS/CFX)方法计算了复合材料螺旋桨在均匀来流下的流固耦合力学性能;He 等[8]利用ANSYS/CFX 软件对比研究了复合材料螺旋桨与金属螺旋桨的流固耦合动力学特性;曾志波等[9]基于边界元理论与有限元法开展了复合材料螺旋桨流固耦合数值方法研究,重点探讨了流固耦合中载荷及几何变形量的传递问题,并与已有文献比较,验证了算法的可行性;熊鹰等[10]采用瞬态计算方法研究了非均匀流场下螺旋桨的流固耦合性能,随后他们又在ANSYS Workbench 平台下,利用ACP 模块和CFX 模块研究了均匀流场下复合材料螺旋桨的流固耦合力学性能,并与实验结果比较,验证了ANSYS ACP 模块分析复合材料螺旋桨流固耦合性能的可行性[11];安邦等[12]基于ANSYS/CFX 软件,利用单向流固耦合方法研究了螺旋桨在水动载荷作用下的结构强度。
对于第二个问题,通常忽略了流体与桨之间的流固耦合效应。同样,国内外对这个问题也做了大量研究:Murawski[13]介绍了使用简单的集总参数模型快速评估船舶推进轴系纵向振动与扭转振动固有频率的方法;Polic 等[14]研究了在冰雪中工作的推进轴系扭转振动响应;Zhang 等[15]利用传递矩阵法研究了推进轴系的纵向振动,探讨了推力轴承刚度及位置对纵向固有频率的影响。在上述研究中,螺旋桨均被简化为一个集中质量单元附加在轴系末端,从而忽略了桨的弹性效应。同时该假设也忽略了桨与轴系间的弹性耦合效应。该处理方法在螺旋桨刚度很大时,有很高的工程精度,这也正是国内外学者广泛采用的原因。目前随着螺旋桨大型化,以及复合材料螺旋桨的出现,螺旋桨变得越来越“柔软”,因此该处理方法将会引入较大的误差。比如李小军等[16]研究了弹性桨-轴耦合系统的固有频率特性,其研究表明桨、轴间的弹性耦合效应对系统固有频率有较大影响;同样,楼京俊等[17]将螺旋桨桨叶简化为梁-弹簧振子模型附在轴系末端,专门研究了桨叶弹性效应对桨-轴系统纵振动力学特性的影响;熊晨熙等[18]研究了螺旋桨在宽带激励下引起的桨-轴-船体耦合振动问题。他们采用质量桨-轴系和弹性桨-轴系两种模型对桨-轴系的纵向振动特性做了细致的对比研究。其研究结果表明,桨、轴系间的弹性耦合效应使得桨-轴系统间出现耦合固有频率。因此,将螺旋桨作为质量单元考虑时,会产生较大误差。
综上所述,目前国内外直接针对流体-弹性桨-轴系统流固耦合振动特性的研究很少,大部分是将其割裂为流体-螺旋桨流固耦合动力学分析以及螺旋桨-轴系统振动特性分析两个问题单独研究。将这一复杂问题割裂开来处理时,将会直接忽略桨-轴系统振动与螺旋桨激励力间的耦合效应。这是因为一方面由于螺旋桨或转轴不可避免地存在偏心,使得船舶推进轴系在绕自身中心线旋转的同时,又发生空间涡动(又称为进动),导致附在其上的螺旋桨也做复杂的空间运动,从而使螺旋桨的进流速度每时每刻都在变化,从而进一步导致流场的不均匀性;另一方面,即使螺旋桨工作在均匀来流中,由于轴系振动带动的螺旋桨运动,同样会诱发螺旋桨和伴流场耦合面间的流体振荡,使螺旋桨进一步产生激励力。
通常来说,当轴系振动幅值非常小且频率很低时,由轴系振动导致的螺旋桨水动力学性能变化可以忽略,此时这种分开处理的方法满足工程要求。而对于大型柔性船舶轴系,由于其细长比通常比较小,轴系振动幅值不能忽略;同时由于大型船舶载重增加,通常选用大尺寸螺旋桨,由此导致的螺旋桨微小偏心都会产生很大的不平衡载荷,从而引起轴系剧烈振动。因此,把流体、螺旋桨和轴系作为一个统一的整体去研究其动力学特性及其演化规律很有必要。
本文的研究目的正是在已有研究的基础上,从流体、螺旋桨及轴系三者间的耦合关系入手,将两个被割裂的问题统一起来,建立一个完整的流体-桨-轴系统双向流固耦合动力学模型。另外,目前已有的针对流体-螺旋桨流固耦合动力学分析的研究文献中,很多是基于商业软件的方法。采用商业软件(比如ANSYS+CFX)计算双向流固耦合问题时,需要大量的计算时间,对计算机性能要求(包括CPU、内存以及存储空间等)非常高。特别是如果在已有的螺旋桨流固耦合模型中更进一步考虑轴系振动影响后,用商业软件的计算时间将进一步急剧增加。因此,本文所建立的流体-桨-轴系统双向流固耦合动力学模型需要具备计算速度快,求解精度高等优点。
1 动力学建模
一个完整的流体-桨-轴系统流固耦合动力学模型涉及螺旋桨流体动力学、螺旋桨结构动力学及转子动力学等多方面理论知识,异常复杂。而对这一复杂耦合系统的动力学建模首先要解决三个子问题:(1)流体-螺旋桨双向流固耦合动力学建模;(2)螺旋桨-轴系动力学建模;(3)轴系振动对螺旋桨激励力反馈作用建模,如图1所示。只有解决了这三个关键子问题,才能在此基础上建立一个完整的流体-桨-轴系统双向流固耦合动力学模型。下面简单介绍这三个子问题,更详细的描述参考文献[19]。
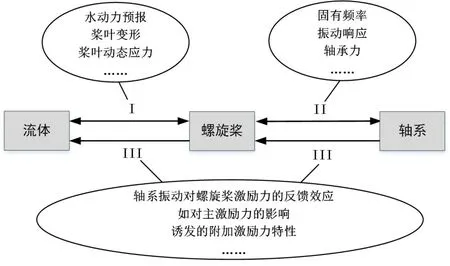
图1 流体-螺旋桨-轴系双向流固耦合建模的三个子问题Fig.1 Three key problems for fluid structure interaction of propeller-shaft system
1.1 桨-轴系统动力学模型
图2 为某船舶推进轴系示意图,其通常由螺旋桨、转轴、后艉轴承、前艉轴承、中间轴承及推力轴承等组成。本文利用有限元方法(FEM)对推进轴系进行动力学建模。其中叶片使用20节点六面体单元;转轴使用Timoshenko 梁单元;轴承简化为弹簧阻尼单元。由于桨毂与转轴属于过盈配合,因此建模时将其当成转轴的一部分,也用梁单元模拟(大量算例表明这种处理带来的误差很小[19])。
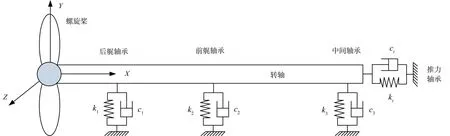
图2 典型的船舶推进轴系示意图Fig.2 Diagram of a typical marine propeller-shafting-bearings system
由于梁单元有六个自由度,实体单元只有三个自由度,因此有限元模型中,叶片与桨毂间的连接需特殊处理,本文采用约束方程实现。对于平面问题,最简单的约束方程如图3所示。
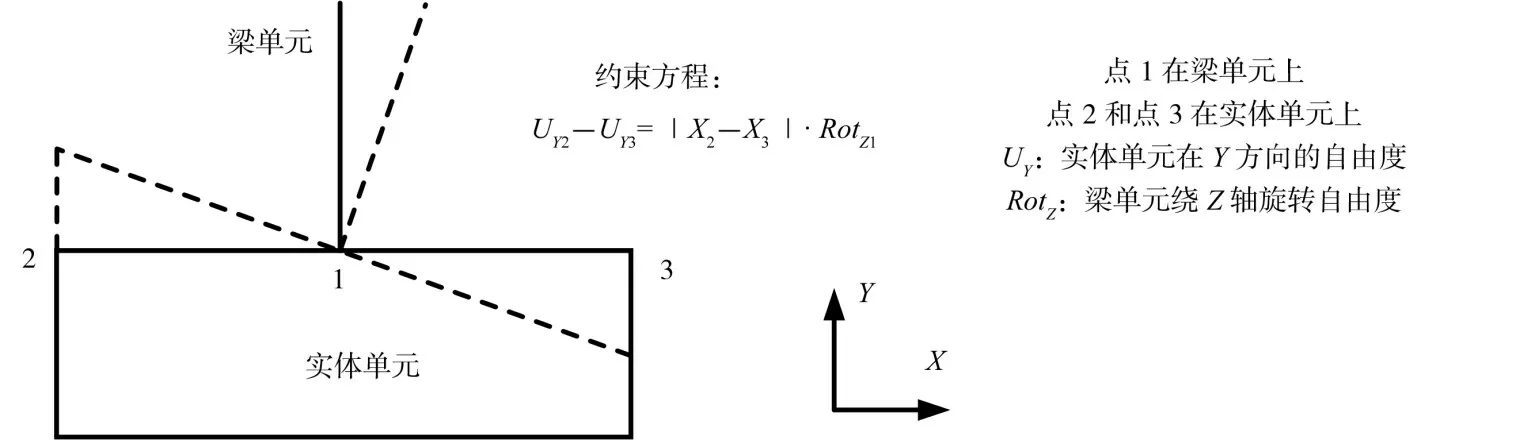
图3 平面梁与实体间的约束方程Fig.3 Link of the beam element and solid element
建好后的桨-轴系统有限元模型如图4所示。其动力学方程可表示为
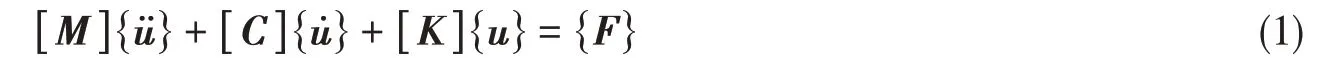
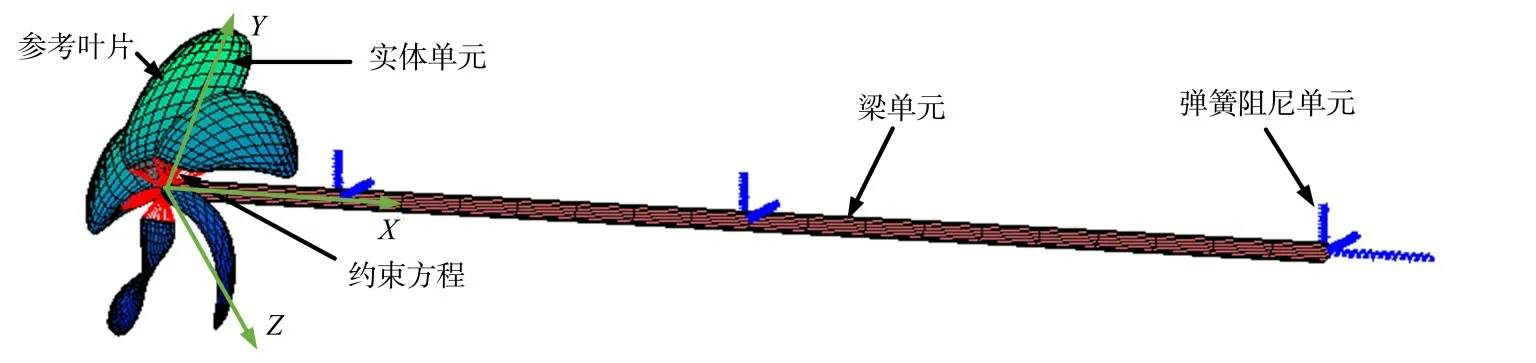
图4 桨-轴-轴承系统有限元模型Fig.4 FEM model of propeller-shaft-bearings system
1.2 流体-螺旋桨流固耦合模型
流场模型用边界元法(BEM,又称为面元法,是基于势流理论的方法)描述。尽管势流理论忽略了流体的粘度与可压缩性,但是大量算例均表明其能取得很好的工程精度,目前已被工程师们广泛应用[20]。假设螺旋桨处于不均匀流场中,如图5 所示。OXYZ 为静止惯性坐标系,其中OX 指向船舶下游。oxyz 坐标系固定在螺旋桨叶片上,随叶片一起旋转。为了避免使用动网格技术,流场求解均在该坐标系中进行。
假设螺旋桨旋转速度为ω,V0表示来流速度。螺旋桨引起的扰动速度势Φ(t)满足Laplace方程:

在螺旋桨表面上满足法向速度为零的运动边界条件,即
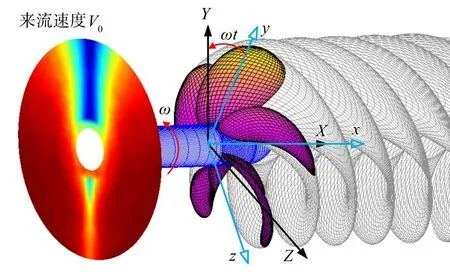
图5 不均匀流场中的螺旋桨及坐标系示意图Fig.5 Fixed and rotating coordinate system and an inflow wake of propellers

式中,Vin= V0+ ω × r 表示螺旋桨进流速度,Vb为螺旋桨叶片的变形速度,其反映了叶片弹性效应的影响。
当Vb≪Vin时,由非定常Bernoulli方程可知,叶片表面压力分布可表示为
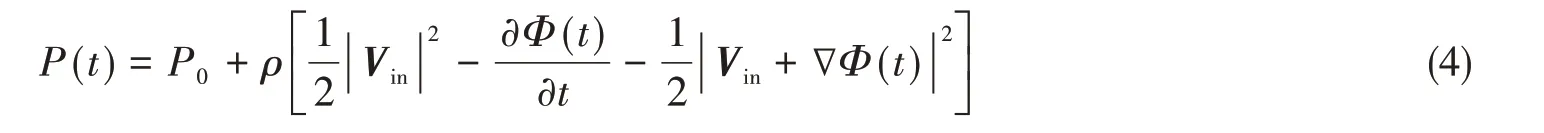
在物体变形不大时,物体与流场间的作用力可以线性分解为刚性物体与流场间作用力(流固耦合界面上不考虑物体的变形)和弹性物体与流场间作用力(流固耦合界面上不考虑物体的复杂运动)的叠加[19],即

式中,φ由进流速度Vin产生;φ由叶片弹性变形速度Vb产生。因此相应的扰动速度势可以分解成两个问题:

忽略高阶小量,则式(4)可分解为


在划分螺旋桨叶片边界元网格时(采用双曲四边形面元,因此一个面元有四个节点),节点布置有限元节点完全一致,如图6 所示,从而使得数据在流场和固体场间传递时更快速、更准确。同时有限元节点与边界元节点均采用余弦方式划分[19]。这样可以保证叶片根部、顶部、导边及随边处的网格更密,从而提高计算精度。
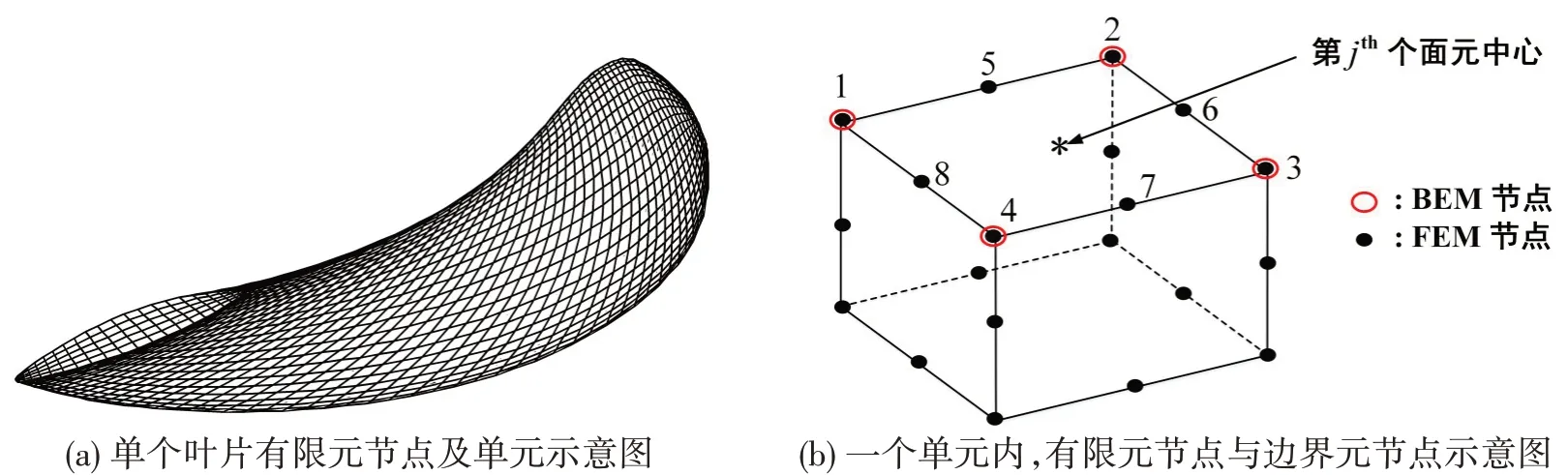
图6 有限元节点与边界元节点示意图Fig.6 Schematic diagram of finite element nodes and boundary element nodes
1.3 轴系振动对流场反馈模型
由于存在外激励(流体激励、不平衡激励、轴承摩擦激励等),船舶推进轴系同时发生弯曲振动、扭转振动及纵向振动等,从而带动螺旋桨一起做复杂的空间运动,使螺旋桨进一步产生激励力。如图7(a)所示,轴系弯曲振动(回旋振动)在转子动力学中又称之为涡动或进动。本文使用转子动力学的理论来描述轴系的空间运动形式,引入三个坐标系,如图7(b)所示。OXYZ为惯性静止坐标系;ox1y1z1为随体坐标系附在叶片上,且始终与OXYZ保持平行;oxyz为随体坐标系,跟着叶片一起旋转,其坐标轴oy与叶片参考线始终重合。由此可知,ox1y1z1由OXYZ平移得到,设平移向量为R=(δx,δy,δz)T。oxyz由ox1y1z1转动得到,设转动向量为Θ=(θx,θy,θz)T。因此轴系末端振动位移可表示为{ }X =[δx,δy,δz,θx,θy,θz]T,其振动速度可表示为{ }X˙ =[δ˙x,δ˙y,δ˙z,θ˙x,θ˙y,θ˙z]T。由转子动力学理论可知:θy=∂δy/∂x,θz=∂δz/∂x。
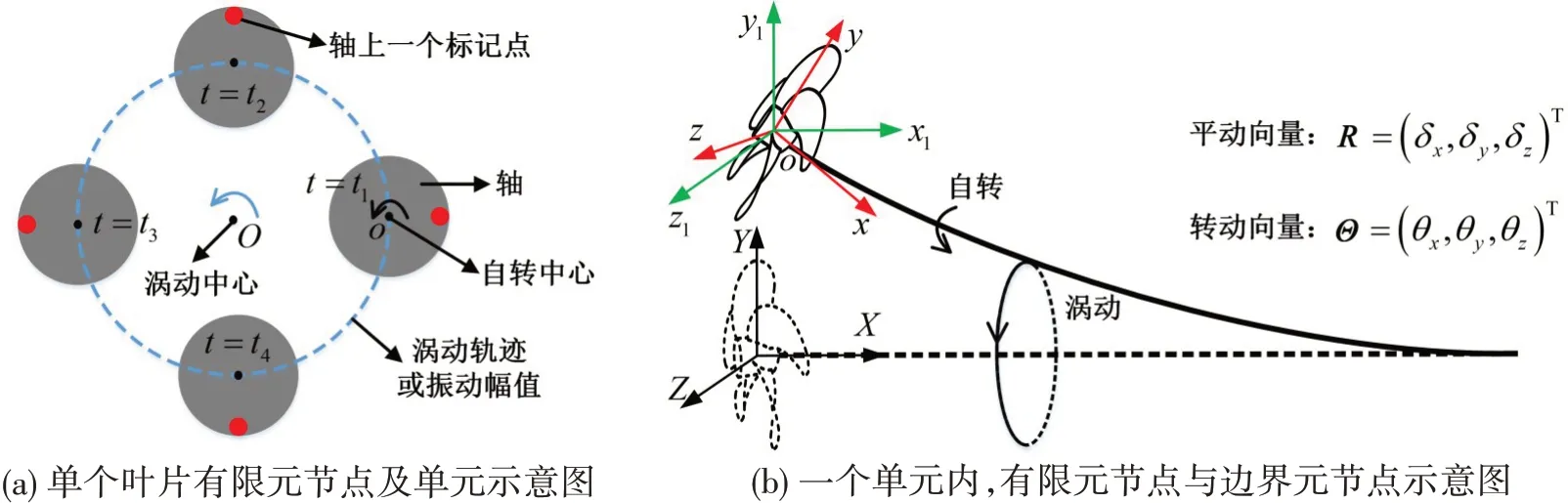
图7 轴系振动与三个坐标系示意图Fig.7 Schematic of shaft vibration and three coordinate systems
坐标系oxyz 与坐标系ox1y1z1的关系可以用投影角法表示[21],如图8 所示。设螺旋桨的自旋轴ox 在x1y1和x1z1平面上的投影线与ox1轴的夹角为θy和θz。θy和θz称之为投影角。坐标系oxyz与坐标系OXYZ的关系可表示为
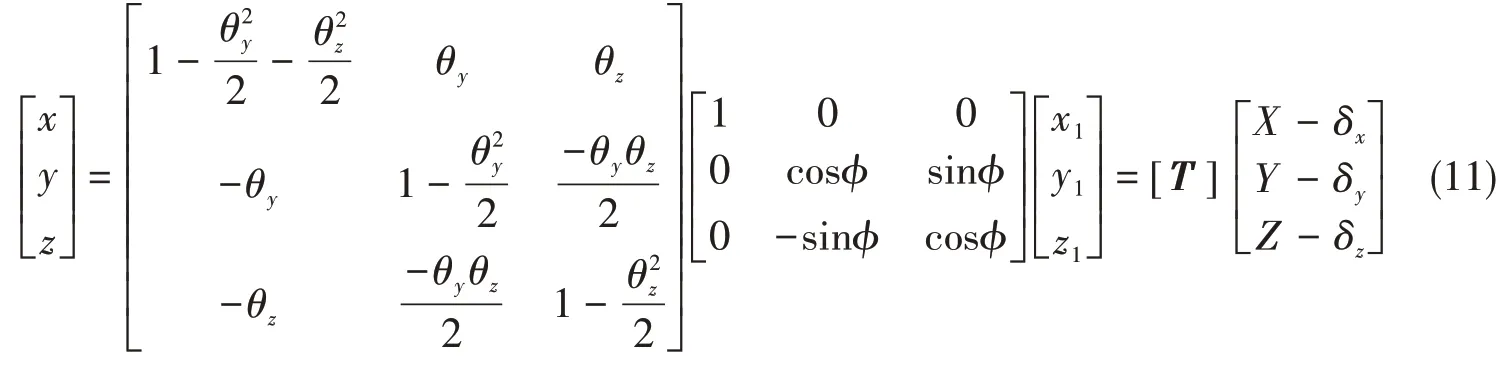
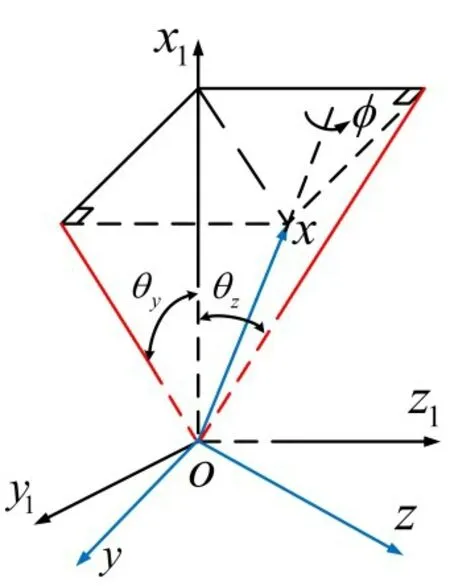
图8 投影角示意图Fig.8 Schematic of projected angle
式中:φ = ωt + θx,ω为螺旋桨的自转角速度;[T ]为旋转矩阵。
由此可见,只要轴系末端位移向量{ }X =[δx,δy,δz,θx,θy,θz]T完全确定,则惯性坐标系OXYZ 与随叶片转动的坐标系oxyz的关系亦完全确定。而轴系的位移只要外激励确定,可以通过1.1节中的有限元方法计算得到。
由式(11)可知,在坐标系oxyz中,螺旋桨叶片表面的速度可以表示为

将式(12)代入式(6),即可考虑轴系振动对螺旋桨进流速度的影响。
对于螺旋桨叶片这种升力体,从叶片随边泄露出的尾涡会影响叶片表面的环量,因此需要考虑尾涡的影响。对尾涡的建模主要考虑尾涡的强度和尾涡的形状。对于传统的根部固定不随轴系运动的螺旋桨,尾涡的形状通常假定为螺旋桨面,泄露的强度通常按Morino 库塔条件或压力库塔条件处理[20]。而对于随轴系做复杂空间运动的螺旋桨,由于其运动轨迹复杂,使得不同时刻随边的位置也不一样,从而从随边泄露的第一个尾涡位置也不断变化。因此需要对尾涡进行合理建模,以便能考虑不同时刻螺旋桨位置及速度变化对尾涡几何形状的影响。
在本文中,假设尾涡的泄露是一个按时间变化的过程,如图9 所示。在初始时刻,假设螺旋桨静止,此时没有尾涡泄露。在Δt时刻,螺旋桨往前移动一个距离,此时泄出第一个尾涡,其强度用简单的Morino 库塔条件表示,即

式中,Δφ(rT)表示叶片半径为rT的随边处泄露的尾涡速度势,φ+(rT)为叶背(吸力面)随边处的速度势,φ-(rT)为叶面(压力面)随边处的速度势。
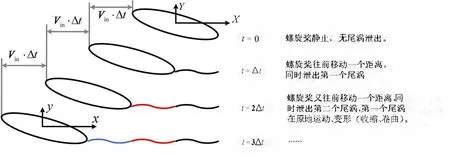
图9 尾涡泄露过程Fig.9 Process of vortex-shedding
在2Δt 时刻,螺旋桨继续往前移动一个距离,此时泄出第二个尾涡,强度仍然按式(13)确定。而Δt 时刻泄露的尾涡其强度保存不变,在原地运动并发生收缩、卷曲等变形。以此时间类推,尾涡的泄露是一个连续的过程。
泄露的尾涡是不受力的,由库塔-茹科夫斯基定理可知,泄露尾涡的速度必定与当地的流场速度平行。也就是说泄露的尾涡片必定按当地的流线运动。在OXYZ 坐标系中,尾涡的运动速度为VW=∇φ。因此泄露的尾涡每个时间步运动的距离为
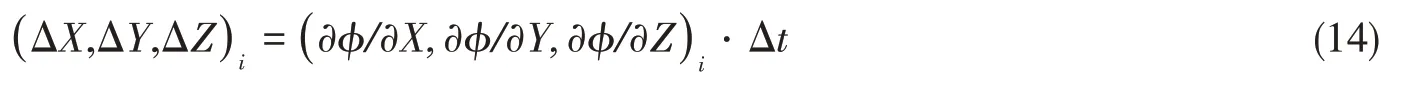
假设螺旋桨共有Z 个叶片,将一个叶片及相应轮毂划分成Np个四边形面元(沿弦向面元数为ns,沿展向面元数为nr,轮毂面元数为Nh,则Np= ns⋅nr+ Nh)。泄露尾涡面元的展向数目为nr,弦向数目由时间总步数nt决定。比如在it个时间步,弦向泄露共it个尾涡面元,其中只有紧靠叶片随边的第一列面元强度未知,其它尾涡面元强度均已知,如图10所示。
因此在第it个时间步,式(6)可离散成
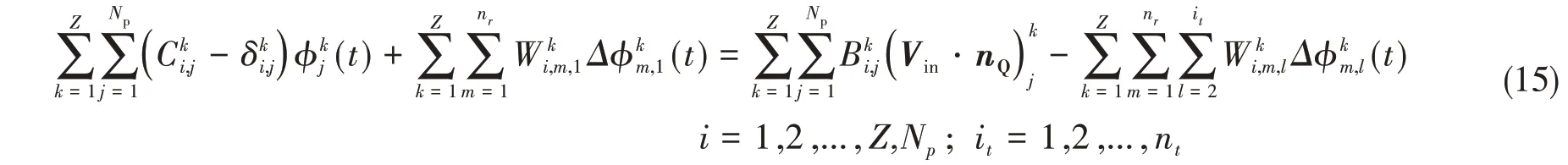
式中:Δφm,1为各叶片上刚泄露出的尾涡强度,Δφm,l为各叶片上之前时间步泄露出的尾涡强度;δi,j为Kronecker 函数,l和为影响系数,定义如下:

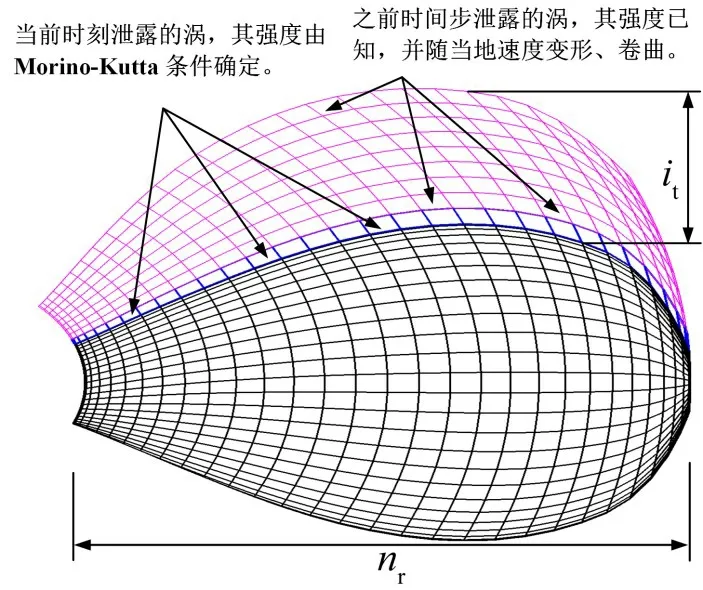
图10 螺旋桨及泄露尾涡面元分布Fig.10 Panel arrangement of propeller and wake
一旦求得φ,即可通过式(8)与式(9)求得水动力载荷{Fφ} 。
1.4 求解流程
至此,图1 中的三个子问题全部解决,将其有机整合在一起,即可建立流体-桨-轴系统双向流固耦合动力学模型。完整的流体-桨-轴系统双向流固耦合动力学方程可写为

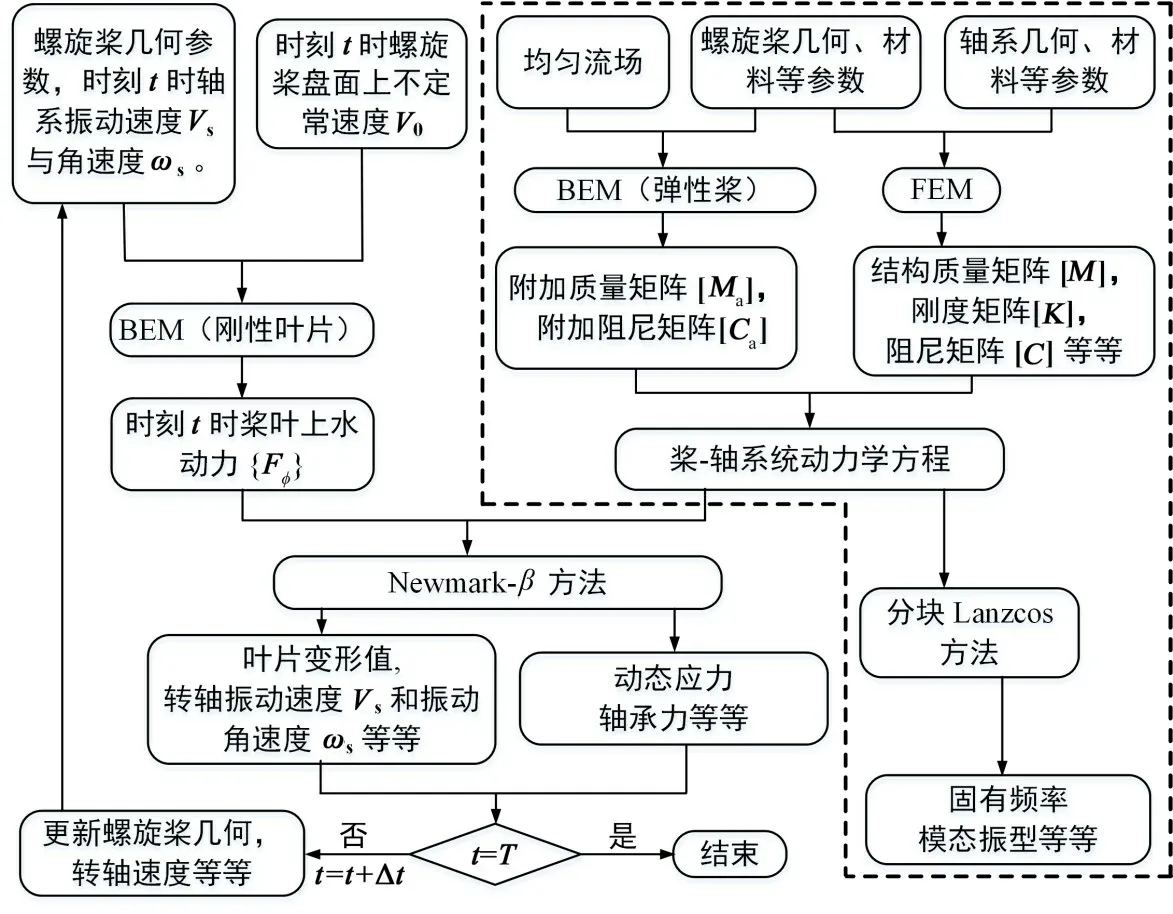
图11 双向流固耦合求解流程图Fig.11 Flowchart of bidirectional fluid structure interaction
虚线框图中螺旋桨有限元动力学模型只需在初始时刻计算一次,这是因为尽管在流固耦合计算过程中,每个时间步的叶片几何形状均不一样,理论上结构质量矩阵及结构刚度矩阵均会变化,但在工程实际中,由于结构变形很小,通常都只需计算初始几何形状的结构质量与刚度矩阵,忽略几何形状导致的几何附加刚度矩阵。只有在变形很大时,才考虑这种几何非线性效应的影响。同样地,本文将这种处理方式也应用于附加质量矩阵[ Ma]和附加阻尼矩阵[ Ca]。当螺旋桨叶片变形不大时,忽略由叶片变形导致的流体附加质量矩阵及附加阻尼矩阵的变化,因此本文按螺旋桨叶片的初始几何(没有变形)形状计算桨叶的附加质量矩阵及附加阻尼矩阵,且只需计算一次。
刚性叶片及轴系振动在非均匀流场中产生的水动力{Fφ} 的求解流程在虚线框图外。由于本文考虑了轴系振动对螺旋桨激励力的影响,因此在每个时间步计算{Fφ} 时,都重新更新了轴系末端振动速度Vs和ωs。同时,本文也考虑了叶片变形对{Fφ} 的影响,并实时更新了叶片的几何数据。
在每个时间步下得到水动力载荷向量{Fφ} 后,通过流固耦合动力学方程就可以求解叶片及轴系的动态响应,本文采用Newmark-β方法求解。得到轴系动态响应后,可以进一步求解叶片的动态应力及轴承支反力等。
2 数值仿真验证
本章只介绍有限几个数值仿真例子,验证本文所建模型及编制程序的正确性(更多算例详见文献[19])。首先通过两个算例验证BEM 模型及程序的正确性;计算时,假设螺旋桨从桨毂处断开,且桨叶为刚性,目的是验证模型中{ }Fφ的求解精度;然后通过两个算例验证FEM 模型及程序的正确性。在此计算时,不考虑水动载荷{ }Fφ的影响。最后通过一个算例,验证了耦合的FEM-BEM程序的正确性。
2.1 BEM程序验证
本小节首先计算P4119螺旋桨在均匀流场中叶片压力分布及敞水性能,并与文献[22]的实验结果比较。计算中,虽然来流是均匀的,但是由于考虑尾涡的时变过程,因此仍然按不均匀来流的方式处理,即按时间步求解。图12 为桨叶各半径处的压力系数计算结果与实验结果比较。从图中可以看出,在叶片导边和随边附近误差较大,这是因为流体在叶片边缘处的流动非常复杂,比如导边分离等,而这些现象在目前的模型中均不考虑。另外在随边处,叶面上下压力差并不相等,这是由于本文采用Morrino库塔条件,而不是压力库塔条件导致的。
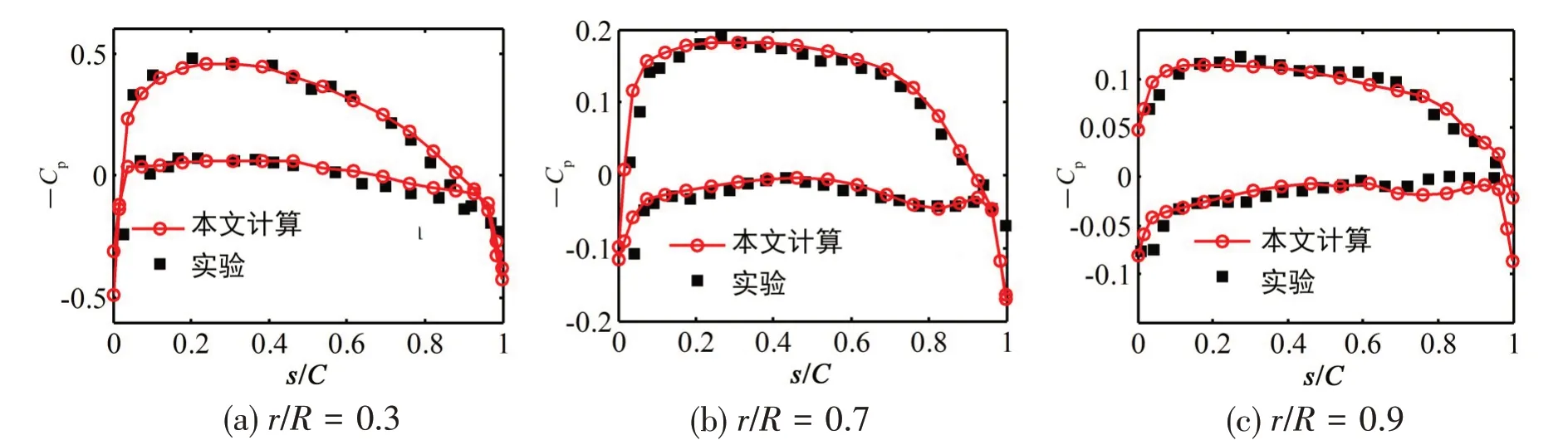
图12 P4119螺旋桨压力系数比较Fig.12 Pressure distribution comparison of P4119(J=0.833)
第二个算例是螺旋桨做纵向振动,振动速度为δ˙x= 0.2V0sin(ωt)。文献[23]中分别用升力面(VLM)和面元法(BEM)对其推力系数与扭矩系数进行了预报。将本文的计算结果与文献[23]的预报结果做比较,以验证本文算法的正确性。将一个叶片弦向划分50 个面元,展向划分30 个面元。其余计算参数(比如计算步长,旋转角速度等)均按文献[23]处理。图13 是计算的脉动推力系数与扭矩系数与文献[23]的结果比较。从图中可以看出,本文的计算结果与其吻合良好,求解精度在工程许可范围以内,从而验证了本文算法的正确性。
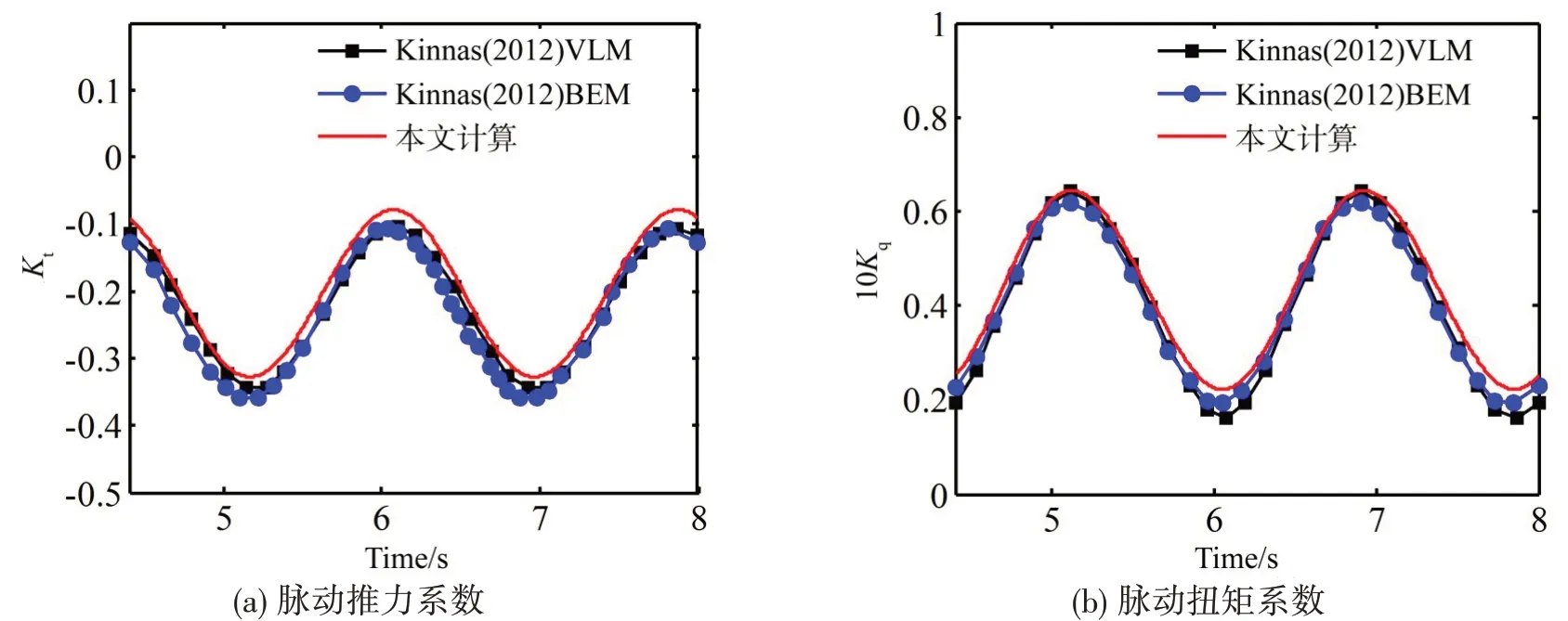
图13 脉动推力系数与扭矩系数比较Fig.13 Comparison of thrust and torque coefficients
2.2 FEM程序验证
第一个算例是计算桨-轴系统在叶片均布载荷下的变形及轴承支反力。均布压力只施加在第一个叶片的叶背(吸力面)上,这种不对称的载荷分布使得各径向轴承上存在支反力。均布压力大小为500 Nm-2。将本文结果与ANSYS计算结果比较。
图14 为5 个桨叶的变形云图,从该图可以看出ANSYS 计算结果与本文计算结果很吻合,最大变形约为2.8 mm。表1为所有轴承上的支反力比较,从表中可以看出相对误差很小。因此,该算例证明了本文的桨-轴系统有限元模型及所编写程序的正确性。
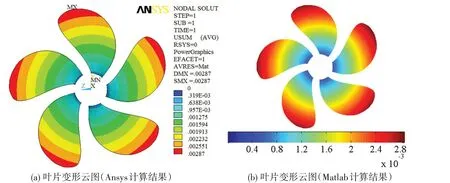
图14 桨叶变形云图比较(单位为m)Fig.14 Comparison of deformation contours for blades(the unit is‘m’)

表1 轴承支反力比较Tab.1 Comparison of bearing reaction forces
第二个算例是比较桨-轴系统在空气中的固有频率及模态振型。表2为轴系各阶固有频率比较。对于弯曲振动,由于横向与垂向的各阶固有频率相同,因此表格中只给出一个方向的值。从该表可以看出,本文模型计算结果与ANSYS 结果间相对误差均很小。更进一步地,图15~17 为各阶振型比较。从中可以看出,按模归一化后的振型不论是最大值还是最大值发生的位置均高度一致。从该算例可以进一步证明本文桨-轴系统有限元模型及所编程序的正确性。

表2 空气中轴系固有频率比较Tab.2 Comparison of natural frequencies of shaft system in air
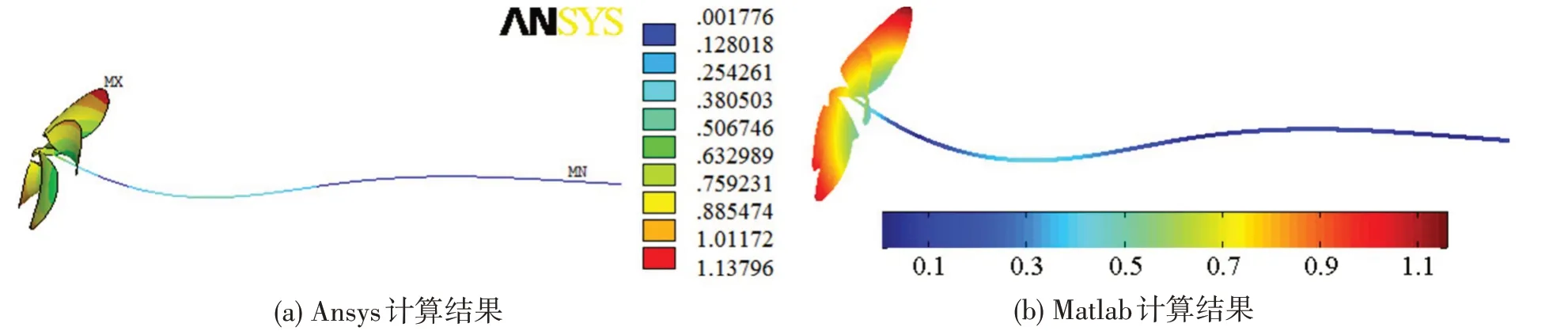
图15 第一阶弯曲振型比较Fig.15 Comparison of the bend modal shape(the first)in air

图16 第二阶纵向振型比较Fig.16 Comparison of the longitudinal modal shape(the second)in air
图17 第二阶扭转振型比较Fig.17 Comparison of the torsional modal shape(the second)in air
2.3 耦合的FEM-BEM 程序验证
流固耦合最典型的特征是流体会引起结构附加质量,从而降低结构的固有频率。因此计算结构湿模态时,需要将BEM(求解流体引起的结构附加质量)与FEM(求结构固有频率)耦合在一起。本小节为了验证耦合的FEM-BEM 程序,计算了螺旋桨的湿模态,并与ANSYS 计算结果比较。选取P438X系列螺旋桨为研究对象,其几何尺寸及材料属性见文献[19]。ANSYS 中,在螺旋桨周围建立一个半径非常大的流体域并用fluid30单元模拟流体产生的附加质量效应。由于本文计算附连水质量时采用的势流理论,即认为水是不可压缩的,因此为了能跟ANSYS 结果比较,在ANSYS 中将声速设为无穷大,以模拟水的不可压缩特性。
计算结果如表3 所示。从该表可以看出,本文模型计算的湿模态结果与ANSYS 湿模态结果差别很小,表明了本文模型以及编制程序的正确性。
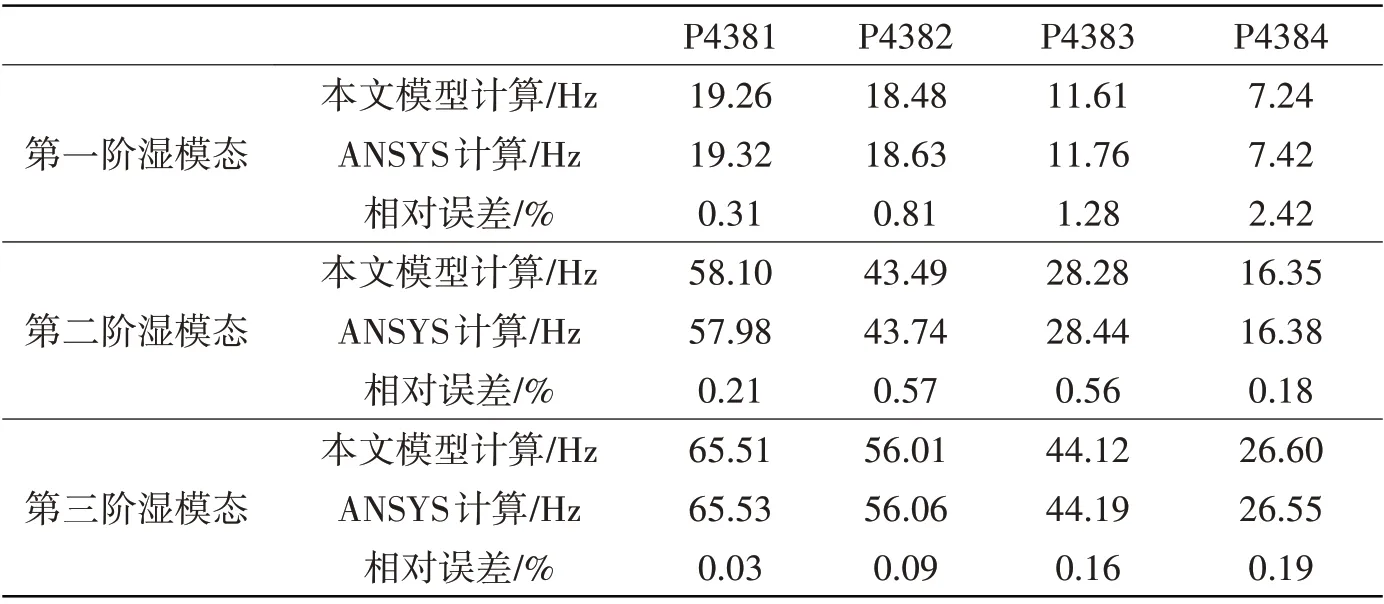
表3 螺旋桨湿模态比较Tab.3 Comparison of natural frequencies of propeller in water
3 实验验证

图18 重力式水洞Fig.18 Gravity tunnel
本章实验测量了桨-轴系统在空气中及水中的固有频率,并与本文模型计算结果比较,从而实验验证本文模型的正确性。本实验在重力式水洞桨-轴振动实验平台上进行,如图18所示。
实验螺旋桨使用P4381桨,该桨用ABS塑料制造,具体尺寸及材料属性见文献[19]。加工的螺旋桨以及传感器布置如图19所示。
采用力锤敲击法测试系统固有频率,测试结果如表4所示。从该表可以看出,总体上两者的相对误差很小(尽管轴系第一阶纵向固有频率相对误差很大,但是其绝对误差很小),从而表明了本文所建立的桨-轴系统动力学模型及所编写程序的正确性。可能的误差来源有以下几个方面:(1)实验测试中的误差;(2)理论计算时,对于轴系而言,由于推力轴承刚度值厂家并没有给定,因此本文的刚度值依据实验结果推测而得,理论计算时本身也会产生误差。

图19 加工的螺旋桨及传感器安装图Fig.19 Machined propeller and sensor installation
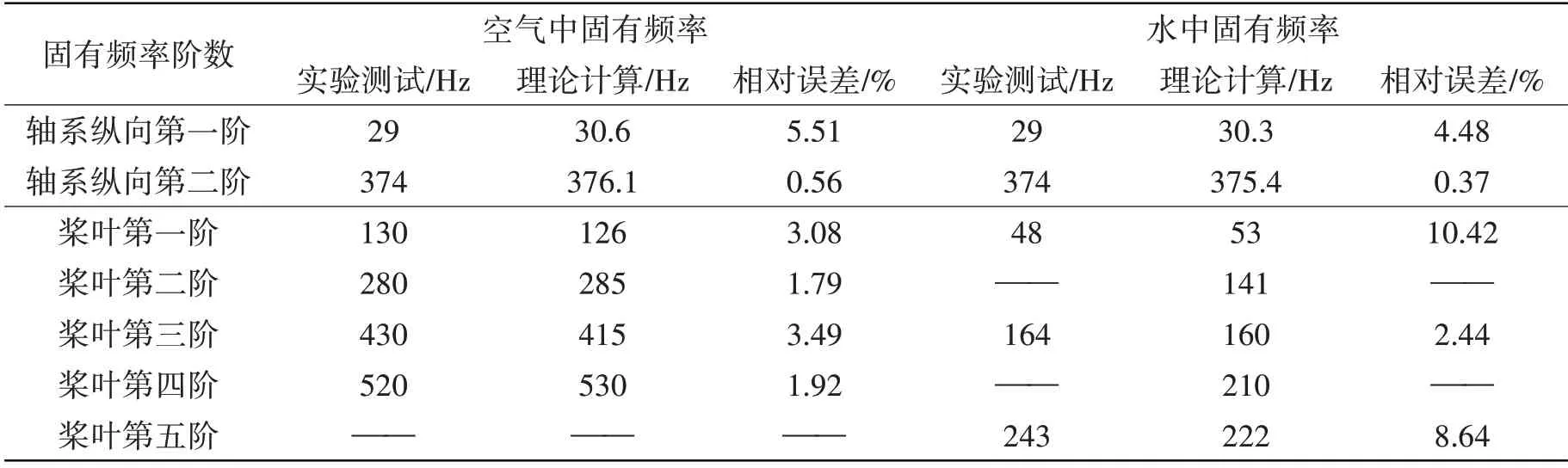
表4 桨-轴系统空气中固有频率理论计算与实验结果比较Tab.4 Comparison of natural frequencies between the experiment and calculation
图20 为塑料桨各叶片在空气中的加速度频响函数实测及拟合结果(仅给出三个叶片的结果)。其中敲击部位为桨叶1的中部,方向为纵向。可以看出受传感器安装位置及敲击部位等因素的影响,各叶片被激起的模态数目也略有差异。同时,不同叶片同一阶固有频率在数值上有差异,实验中发现这是受传感器附加质量的影响。因此表4中的理论计算结果考虑了传感器的附加质量影响。
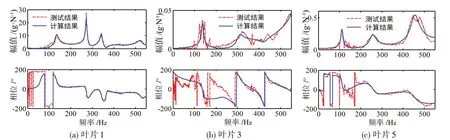
图20 桨-轴系统空气中加速度频响曲线结果(桨叶上)Fig.20 Results of acceleration FRF for propeller-shaft system in air(on the blade)
图21为纵向敲击桨三个不同叶片中部时,被敲击叶片在水中的加速度频响函数实验测试及拟合结果。实验测试时,桨叶第二阶及第四阶模态并没有被测到,这是受传感器安装位置的限制(仿真分析时发现这两阶模态均是叶片边缘的局部共振)。
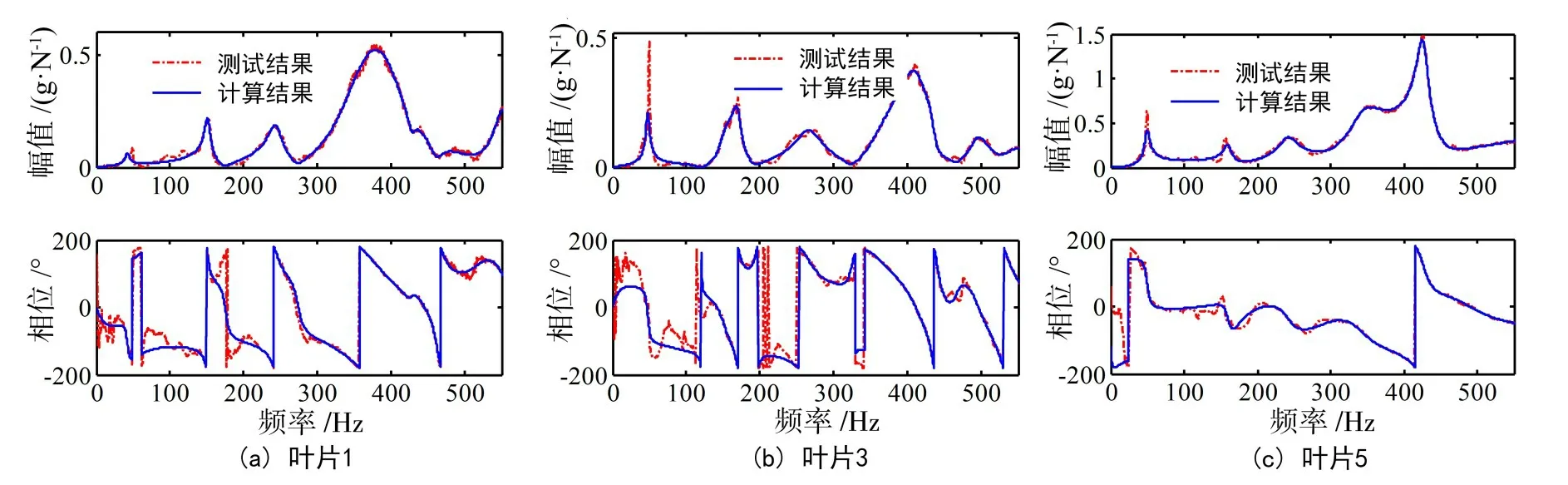
图21 桨-轴系统水中加速度频响曲线结果(桨叶上)Fig.21 Results of acceleration FRF for propeller-shaft system in water (on the blade)
4 结 语
本文考虑流体、桨、轴系间的复杂耦合关系,利用有限元法(FEM)耦合边界元法(BEM)建立了桨-轴系统双向流固耦合动力学模型。通过数值仿真分析与实验研究,验证了所建模型的正确性。本文所建立的模型可以为揭示螺旋桨激励力产生、传递机理及桨-轴系统流固耦合振动演化规律提供理论计算模型,从而能更进一步掌握螺旋桨激励力引起的低频噪声成因。
同时研究发现本文建立的双向流固耦合动力学模型相比于目前广泛采用的商业软件方法具有计算速度快、对计算机性能要求低等优点,且计算精度满足工程要求。这是因为:(1)本文的模型中,流场采用BEM 建模,只需对物体的边界划分面网格,因而可大量节省数据存储空间,减少了计算量;(2)BEM 网格是基于FEM 网格最外层“剥离”生成,因此可保证边界元网格与有限元网格节点一一对应,从而使两种场之间的数据传递无需插值处理,使得数据传递更快、更准确;(3)整个流场求解均在旋转坐标系中进行,最后将结果转换到全局坐标系,可避免使用滑移网格或者动网格技术。总之,本文建立的桨-轴系统双向流固耦合动力学模型是一个快速的、适合工程应用的计算模型。
