波流联合作用下深海垂直杆件三维振动响应分析

刘浩宇，唐友刚，李 焱，曲晓奇

（天津大学a.建筑工程学院；b.水利工程仿真与安全国家重点实验室，天津300072）

0 引 言

垂直杆状结构被广泛地应用于海洋工程领域，如深海立管、张力腱等，该结构安装在水深1 000 m以上深水中，遭受波流和顶部浮体（平台本体）的升沉作用。随着水深的增加，该类结构的安全性和稳定性问题越来越突出。其中，杆件的参激-涡激联合振动问题尤其吸引了人们的关注。本文将此类结构抽象为统一的力学模型，即遭受波流和顶部浮体升沉作用的深海杆件来进行研究。

杆状结构在流场中会与尾流产生相互作用，产生涡激振动，涡泄频率满足斯特罗哈尔关系。当涡激振动频率接近杆件振动固有频率时，斯特罗哈尔关系不再适用，涡泄频率会被“锁定”（lock-in）在杆件固有频率附近，并伴随大幅谐振，即“锁定（lock-in）效应”，这类问题已经被广泛关注[1-3]。

近年来国内外学者针对深水杆件的涡激振动问题进行了实验研究和理论分析。Lie[4]在挪威深水码头进行了大尺度立管涡激实验，对立管顺流和横流两个方向振动进行了观测研究。Dong等[5-6]研究了波流联合作用下张力腿的涡激非线性振动，并分析了涡激频率接近张力腿固有频率时，杆件振动的稳定性问题，研究表明，随着阻尼减小和升力系数增大，系统趋于不稳定，结果中出现多解区域，并伴随有跳跃现象。

当杆件顶端的平台浮体发生升沉运动时，杆件会受到轴向动力激励，这种激励被称为参数激励。由于参数激励引起的运动边界的非线性[7]，杆件的涡激振动会变得更加复杂[8-9]。Chatjigeorgiou 等[10]研究了简谐参数激励对垂直杆件横向振动的影响，研究表明，参数激励激发新的不稳定区，非线性阻尼无法有效地抑制横向振动失稳的发生；Lei 等[11]采用频域方法，求解了变张力和波浪力联合作用下立管的横向振动方程，发现了参数激励的存在会对立管的波浪激励响应产生影响；唐友刚等[12]考虑了立管顶端的动边界条件，建立了顶张力立管模型，研究了其参激-涡激耦合振动的动力特性，发现横向振动响应频率中，存在1/2 倍参激亚谐成分；张杰等[13-15]针对深海立管受到参激作用时，深海立管的固有振动特性、稳定性以及多模态耦合特性展开一系列的研究，结果表明，在参数激励作用下，立管固有振动特性发生改变，不稳定区域增加。

目前的研究工作，一般是考虑涡激振动或者涡激振动及参激振动，即研究杆件的二维振动。本文综合考虑波流向、涡激方向及参数激励方向，建立深海杆件的三维振动方程，针对杆件不同的顶端边界条件和环境条件，分别对立管波激-涡激振动和波激-参激-涡激联合振动进行数值模拟。采用数值解法对方程进行求解，分析了深海杆件在波流和参激作用下的振动特性。

1 深水杆件三维振动方程的建立

本文基于Han等[16]提出的柔性梁非线性振动模型，如图1所示，将杆件等效为柔性等截面梁，长度为L。杆件顶端受到x 方向张力NT= N0+ N，N0为预张力，相应的预应变用ε0表示，N 为动张力，NT表示参激作用力，杆件底端与海底铰接。

图1中，OM = s，M点的位移向量在x、y和z方向的投影分别为u、v和w，满足：

图1 垂直杆件理论模型Fig.1 Theoretical model of vertical flexible beam

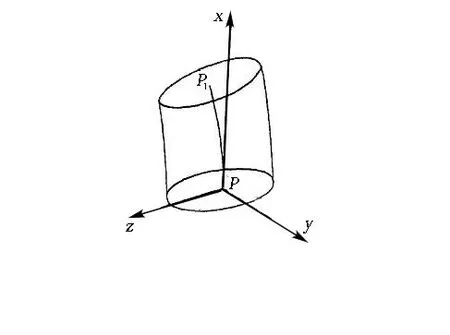
图2 杆件局部变形示意图Fig.2 Local deformation of vertical flexible beam

假定轴向变形与弯曲变形均不可忽略，且满足：

忽略杆件的剪切应变，将式（2）代入格林应变公式，有

根据Hamilton原理，有

式中的拉格朗日函数Lan表达式如下：

即

杆件的应变能EP为

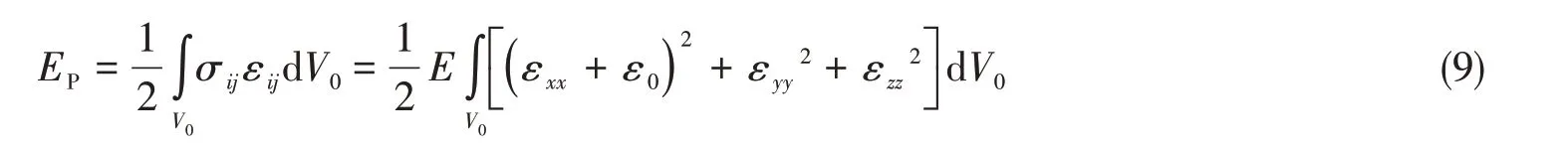
杆件的动能Eκ为

式中，IZ和IY为截面惯性矩，IYZ为截面惯性积。

外力虚功δW为

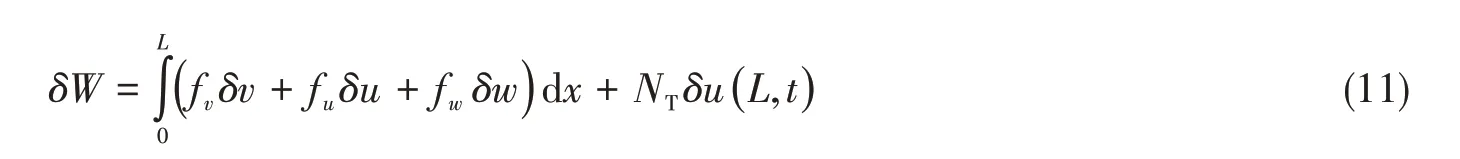
式中，fu为杆件在水中轴向单位长度的重量，fv和fw分别为作用在杆件单位长度上的波流力和涡激升力。

将式（9）～（11）代入式（6）化简后，得到

式中：ρ为杆件密度；A 为横截面面积；EA 为轴向刚度；EI为弯曲刚度；u'、u″和u″″为u对杆长s的一次、二次和四次导数¨和分别为u、v和w对时间t的二次导数。

考虑杆件下端为简支，得到杆件下端的边界条件如下：

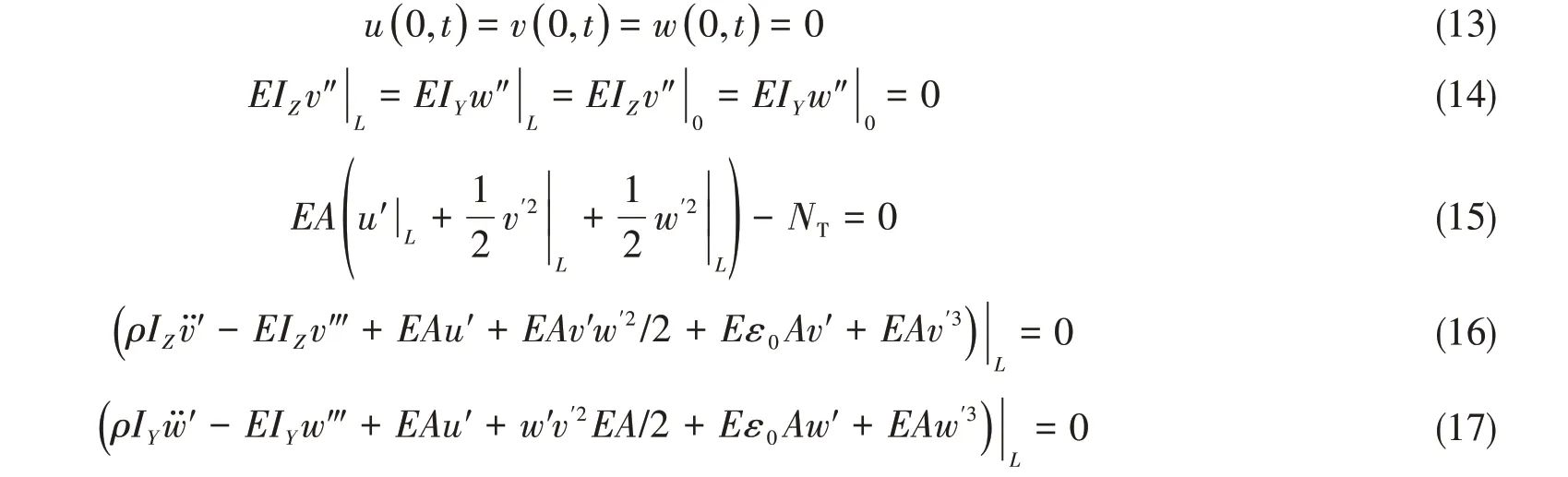
2 环境载荷

杆件受环境载荷示意图如图3 所示。波浪和流场沿y 轴负方向，波浪为Airy 波，波幅Aw，波频ω；海流采用剪切流模拟，表面流速为U0，不同水深处的流速为U - U0( )1 - x/L ；涡激力沿z 轴方向；重力G 沿x轴负方向，顶端参激力NT沿垂向作用。

根据Airy 线性波理论，波浪场中水质点速度满足：

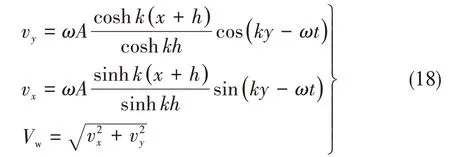
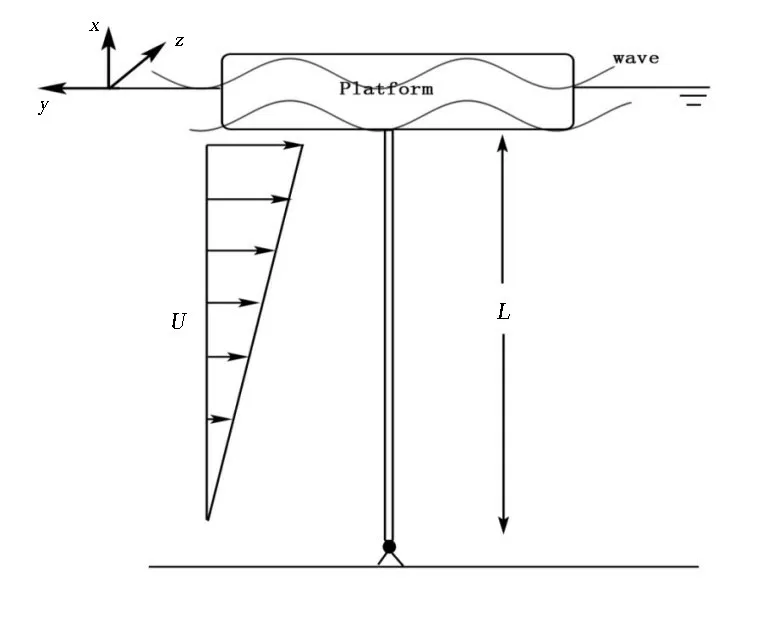
图3 杆件环境载荷示意图Fig.3 Environment load on the beam

式中，h为水深，k为波数，ω为波频，满足色散关系：

采用Morison 方程来表示海流和波浪在y 方向产生的非线性力：

式中，AI= πρD2/4，AD= πD/2，D 为杆件外径。CD为拖曳力系数，CA为附加质量系数，CM为质量系数；V˙w为波浪加速度在垂直于杆件轴向方向的分量，r¨为杆件振动加速度在垂直于杆件轴向方向的分量。杆件z向的涡激升力按照下式计算：

式中：CL为涡激升力系数，这里取0.3；ωvor为涡泄频率，满足ωvor= St ⋅V/D，St为斯特罗哈尔数，取0.2；φ取180°。

假定杆件全部浸没在水中，单位长度杆件的湿重为m，则杆件在x向受到的单位长度重力为

将式（18）代入式（19）～（20），可以求得杆件的激振力，考虑边界条件式（13）～（17），求解式（12），可以得到杆件任意时刻波流和涡激力共同作用下的三维振动响应。

3 算例分析

本文选取深水垂直杆件的参数如表1所示。

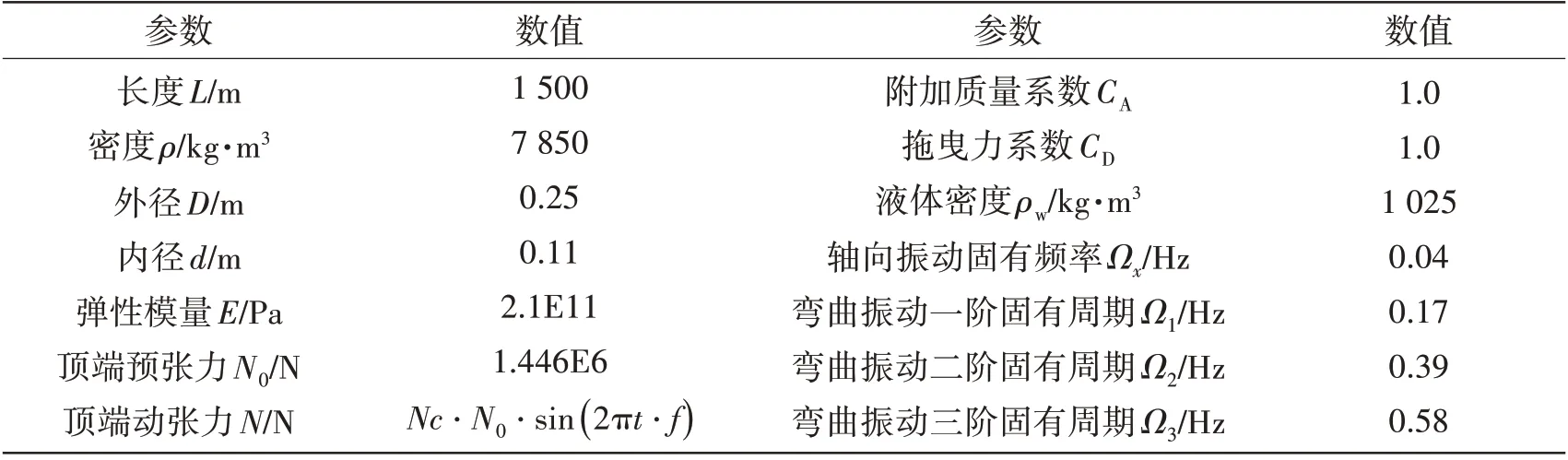
表1 杆件参数Tab.1 Main parameters of the beam

3.1 流速对杆件振动的影响

不考虑参激作用，取式（15）中动张力N=0，NT=N0。规则波波浪周期为5.88 s，波高为5 m，表面流速从0.1 m/s 到1.0 m/s 变化，计算杆件在波、流和涡激作用下的振动响应。杆件中点振动响应幅值统计结果如表2 所示，从表中可以看到，随着流速的增加，流力增大，杆件在波流作用下，拖曳力方向的振幅和平衡位移逐渐增大。其中，平衡位移主要受流力作用，所以增幅较大，而振幅受波激力幅值影响，所以增幅不大。在轴向和涡激振动方向，表面流速为0.4 m/s 和0.9 m/s 时，振幅较大，根据斯特罗哈尔关系可以计算出，在该表面流速下，中点涡激频率分别为0.16 Hz和0.36 Hz，接近立管振动的前两阶固有频率。

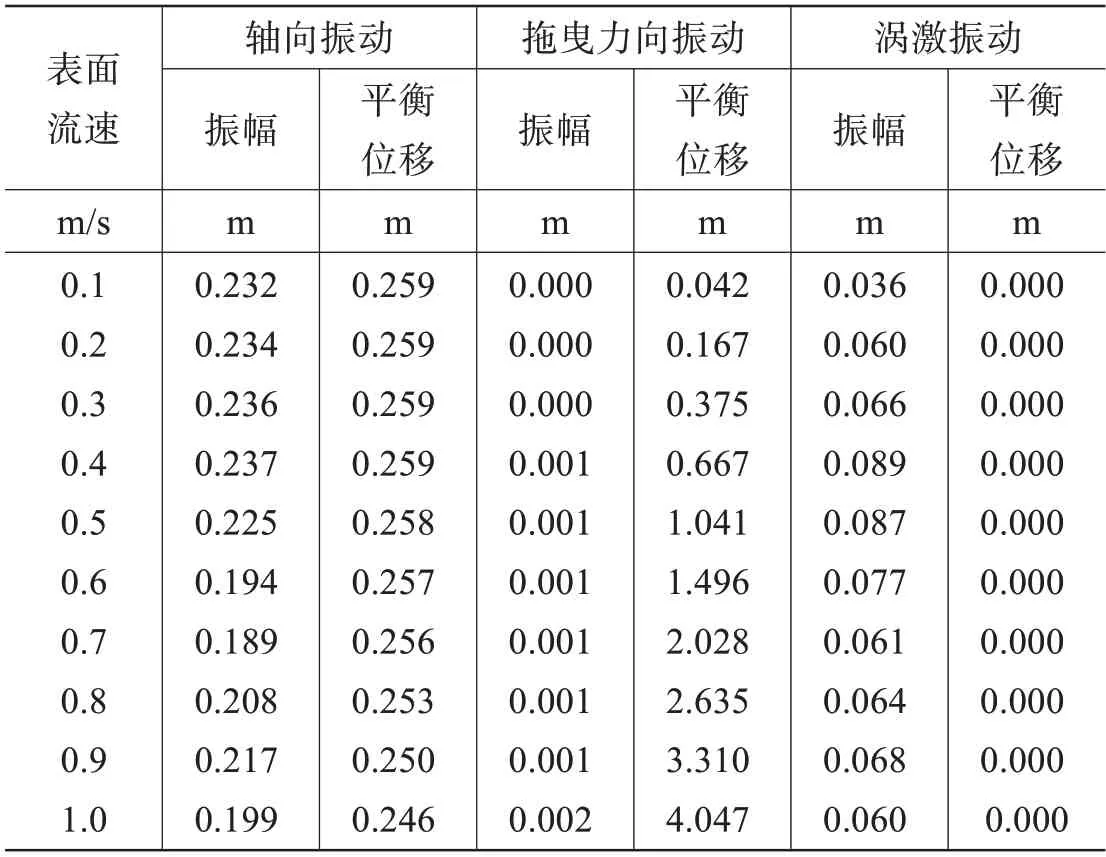
表2 各流速下杆件中点振幅统计Tab.2 Maximum middle point amplitudes under vortex-induced excitation

流速为0.4 m/s 时，杆件中点轴向振动时历曲线和能量谱如图4 所示，该方向振动含有多个频率成分，其中，Ω =0.043 6 Hz，为轴向固有振动频率，图中，ω1=0.010 67 Hz=1/4Ω，ω2=0.0213 Hz=1/2Ω，说明由于结构的非线性特性，中点处轴向振动存在1/2和1/4亚频谐振。

流速为0.4 m/s 时，杆件中点在拖曳力方向的振动时历曲线以及能量谱如图5 所示，从图5（a）可以看出，该方向振动含有多个周期成分，能量频谱图5（b）中存在两个峰值，ω1=0.17 Hz，对应波浪频率，ω2=0.34 Hz=2ω1，即中点处拖曳力方向振动存在2 倍波激频率振动成分，说明波浪激励在拖曳力方向激起了杆件的2/1超频谐振，杆件做类周期振动。

图4 杆件中点轴向振动曲线（无参数激励）Fig.4 Axial vibration of the middle point

图5 杆件中点拖曳力方向振动曲线（无参数激励） Fig.5 Middle point vibration along drag direction

图6 杆件中点涡激振动曲线（无参数激励）Fig.6 Vortex vibration of the middle point

流速为0.4 m/s 时，杆件中点的涡激振动时历曲线和能量谱如图6 所示。从图6（a）可以看出，振动不存在明显的周期性，图6（b）中点振动功率谱存在多个峰值，说明了涡激振动极不规则，存在强非线性。通过斯特罗哈尔关系可以计算出该点涡激频率为0.16 Hz，但由于杆件在剪切流中，各点所受涡激载荷的幅值和频率均不相同，且相互影响，使得杆件中点振动存在多个频率成分。

3.2 参数激励对杆件振动的影响

考虑参激作用，取式（15）中动张力NT= N0+ Nc⋅N0⋅sin( )2πt ⋅f ，参激频率f 取0.17 Hz，张力比Nc取0.2，波流参数与3.1 节相同，计算杆件在波、流、涡激和参激作用下的耦合振动响应。杆件振动响应幅值统计结果如表3 所示，从表中可以看到，存在参数激励时，杆件拖曳力方向振幅和平衡位移均随流速增大而增加；轴向振动和涡激振动的平衡位移受流速影响不大，而振幅在流速为0.4 m/s和0.9 m/s时达到最大，说明发生涡激谐振时，轴向振动和涡激振动的振幅均大幅增加。

表3 参激作用下杆件中点最大振幅统计Tab.3 Maximum middle point amplitudes under parametric excitation

对比表2～3中三个方向的振幅可以看到（图7），同流速下，存在参数激励时，杆件的振幅更大。

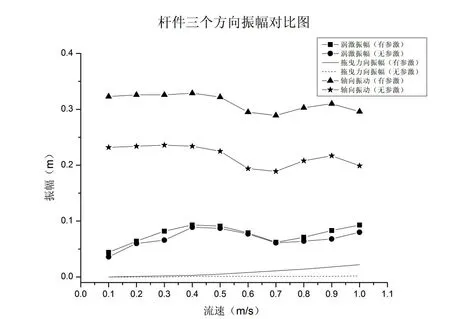
图7 杆件振幅对比图 Fig.7 Comparison of the amplitudes

图8 杆件中点轴向振动曲线（参激频率0.17 Hz）Fig.8 Axial vibration of the middle point

流速为0.4 m/s时，杆件中点轴向振动时历曲线以及能量谱如图8所示，该方向振动含有多个周期成分，能量频谱图8（b）中存在四个峰值，其中，最大谱峰值ω3=0.17 Hz 对应轴向参数激励频率。这表明，由于轴向激励作用，轴向振动大幅增加。

流速为0.4 m/s时，杆件中点在拖曳力方向和涡激振动方向的振动时历曲线以及能量谱如图9和图10所示。从图9可以看到，在参数激励影响下，拖曳力方向振动仍表现出类周期性，能量谱中包含波激频率振动和2倍波激频率振动。参激频率和波激频率叠加，导致能量谱中振动成分不变，谱峰增加。

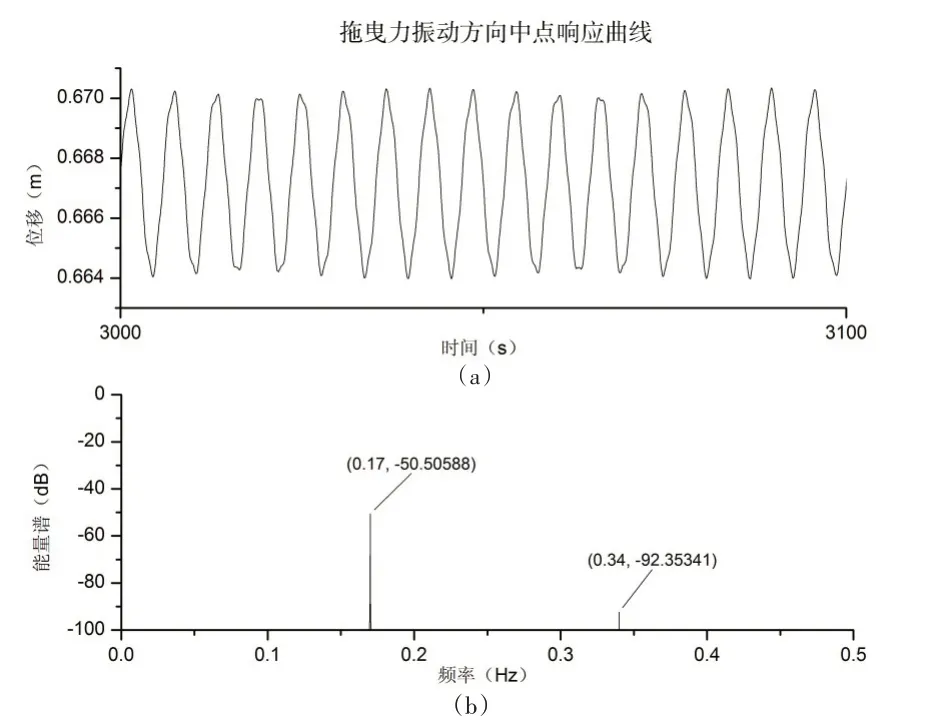
图9 杆件中点拖曳力方向振动曲线（参激频率0.17 Hz） Fig.9 Middle point vibration along drag direction

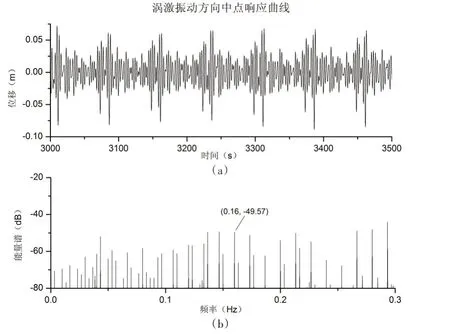
图10 杆件中点涡激振动曲线（参激频率0.17 Hz）Fig.10 Vortex-induced middle point vibration

3.3 参激频率对涡激振动影响

流速为0.4 m/s时，取式（15）中动张力NT= N0+ Nc⋅N0⋅sin( )2πt ⋅f ，改变参激频率f，张力比Nc取0.2，波流参数与3.1 节相同，计算杆件在波、流、涡激和参激作用下的耦合振动响应，杆件振动响应统计结果如表4 所示。从表中可以看到：杆件轴向振动和拖曳力方向振动的幅值和平衡位移受参激频率影响不大；涡激振动方向的振幅在参激频率接近立管固有频率时显著增加。

表4 不同参激频率作用下杆件中点最大振幅统计Tab.4 Maximum middle point amplitudes under parametric excitation

流速为0.4 m/s 时，参激频率f 取0.1 Hz，从图11（b）中可以看到参激振动成分，杆件中点拖曳力方向和涡激振动方向的振动时历曲线以及能量谱如图12～13 所示，从图12 能量谱中可以看到，拖曳力方向的振动中含有参激振动成分。

3.4 参激幅值对杆件振动影响

取 式（15）中 动 张 力NT= N0+ Nc⋅N0⋅sin( 2πt ⋅f )，参激频率f 取0.17 Hz，改变张力比Nc，波流参数与3.1节相同，计算杆件在波、流、涡激和参激作用下的耦合振动响应。结果如表5 所示，从表中可以看到，杆件平衡位置不受参激幅值的影响，而振幅均随参激幅值的升高而增大。

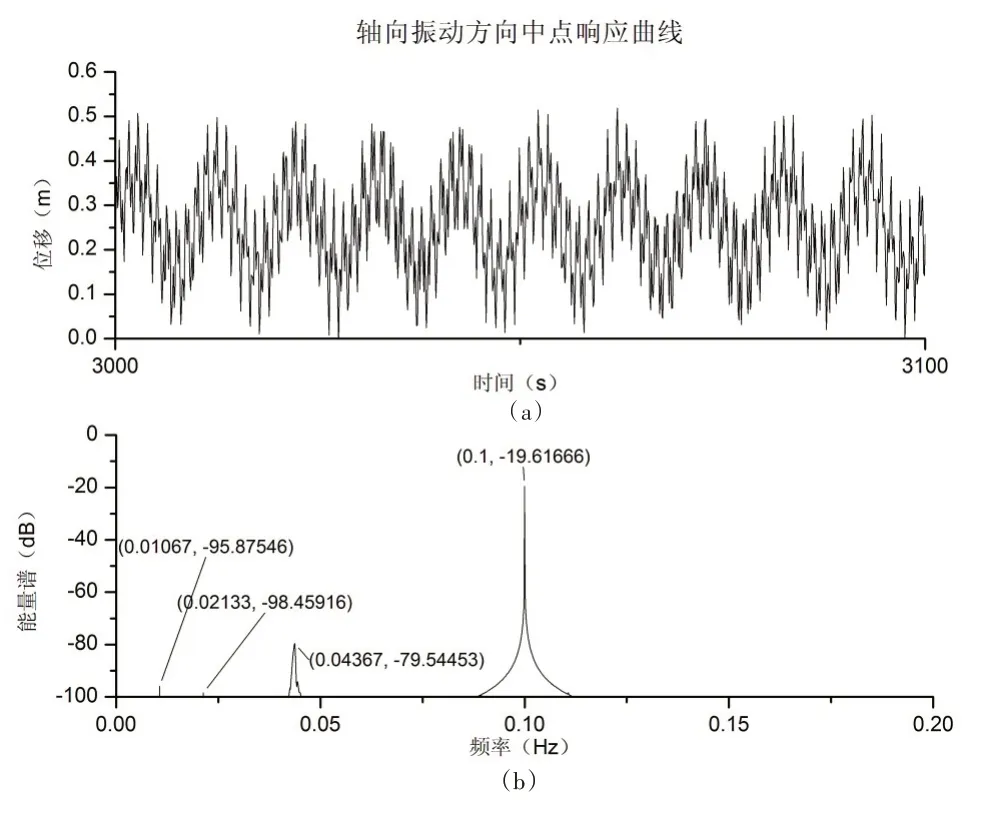
图11 杆件中点轴向振动曲线（参激频率0.1 Hz）Fig.11 Axial middle point vibration

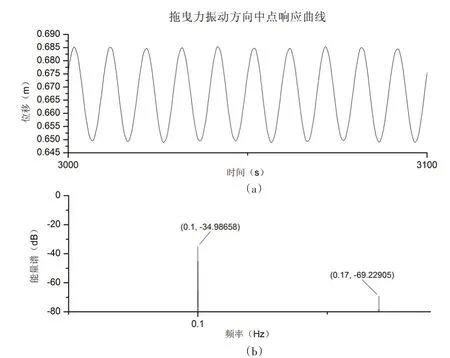
图12 杆件中点拖曳力方向振动曲线（参激频率0.1 Hz） Fig.12 Middle point vibration along drag direction

图13 杆件中点涡激振动曲线（参激频率0.1 Hz）Fig.13 Vortex-induced middle point vibration

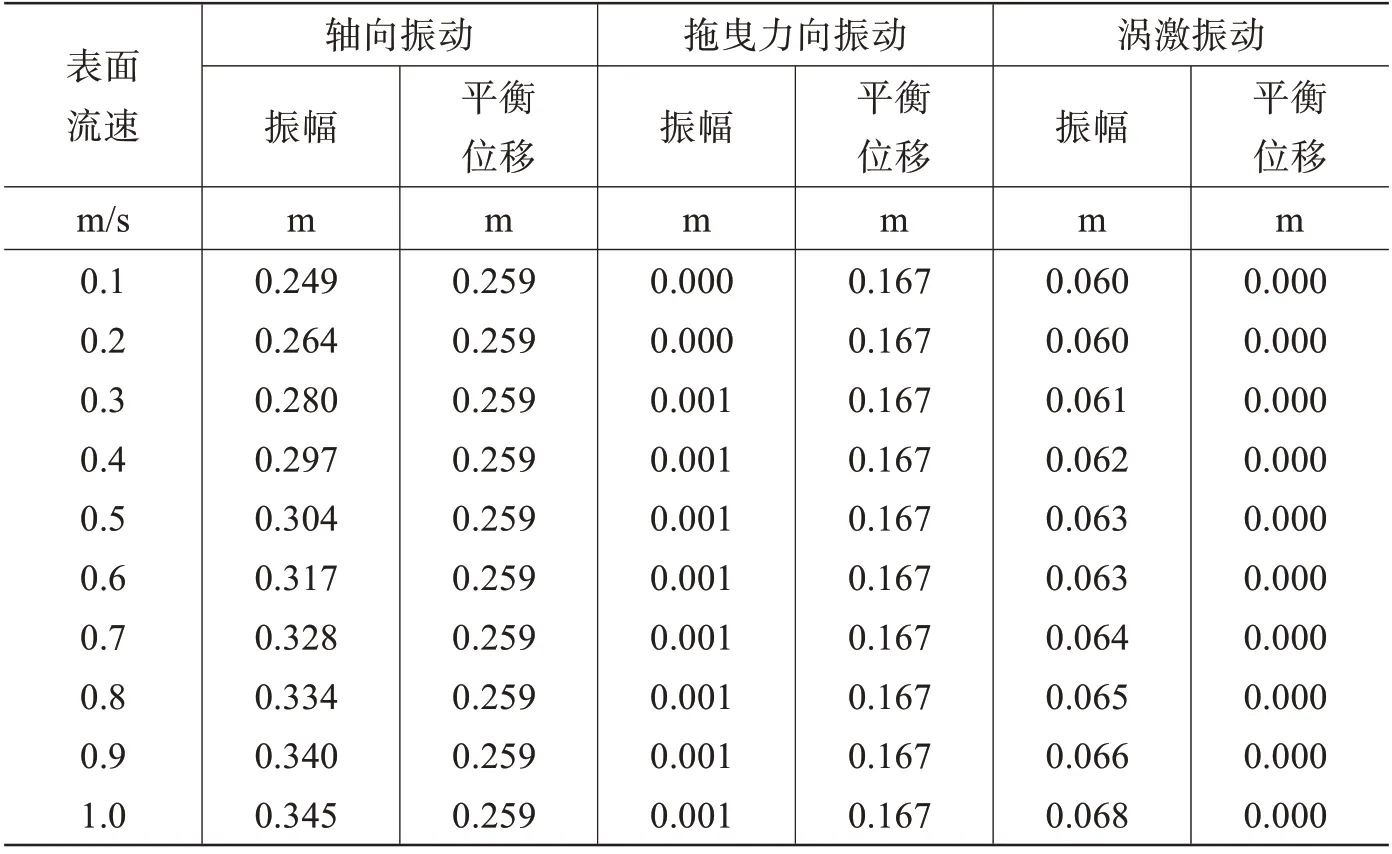
表5 各流速下杆件振幅最大值统计Tab.5 Maximum middle point amplitudes under parametric excitation

4 结 论

本文分析了深海垂直杆件在波流作用下的波激-涡激-参激耦合振动特性，通过对比不同环境条件下杆件的振动响应，研究了流速、参激频率和参激强度对杆件振动幅值和振动特性的影响，得到如下主要结论：

（1）无参激作用时，杆件在波流联合作用下，拖曳力方向的振幅和平衡位移随流速增加而增大，轴向振动和涡激振动的振幅与涡泄频率相关，在发生涡激谐振时，振幅增加。

（2）杆件中点振动表现出强非线性，在轴向振动方向除了固有振动频率外，还存在1/2和1/4亚频成分；拖曳力方向振动为类周期振动，杆件在该方向振动包含波激振动和2 倍波激频率振动，而涡激振动极不规则，振动含多个频率成分。

（3）存在参数激励时，杆件三个方向的振幅均有所增加，其中拖曳力方向振幅增加明显。杆件振动特性不发生改变，时历曲线上的振幅以及能量频谱峰值增加。

（4）杆件在参数激励作用下，拖曳力方向振动中会含有参数激励振动成分；当参激频率发生变化时，拖曳力方向的振幅和平衡位移改变较小；当参激频率接近杆件z向振动的固有频率时，涡激振动和轴向振动的振幅大幅增加。

（5）三个方向的振幅均随参激强度的增大而增加，平衡位移不受参激振幅的影响。