电磁-气囊主被动混合隔振系统抗冲击设计研究

马建国，帅长庚，李 彦

（1.海军工程大学振动与噪声研究所，武汉430033；2.船舶振动噪声重点实验室，武汉430033）

0 引 言

舰船动力装置的抗冲击性能是评判舰船生命力的标准之一。从19 世纪开始国外就对舰船的抗冲击性能展开了研究，并陆续制定了严格的冲击设计规范和标准[1]。各国对舰船抗冲击的研究分为两类：试验法和理论分析方法。在试验法中，美国、英国、德国、荷兰和法国属于全面实战模拟考核体系，而瑞典的海军舰船冲击考核属于典型试验考核体系，目前两个考核体系有相互交融的趋势。理论分析方法[2]主要包括静态等效法、动力设计分析方法（Dynamic Design Analysis Method，DDAM）和实时模拟法。与其它方法相比，实时模拟法是将标准中规定的冲击载荷或实测的冲击时域数据作为输入，分析设备的瞬态响应，从而得到冲击位移、最大加速度等参数。比如在1994年Shaw[3]通过实时模拟法分析了船舶在遭受冲击时，其雷达天线的响应，并依据计算结果给出了整改的措施。主被动混合隔振系统在研制阶段，很难得到冲击的实测数据，所以一般采用国军标的相关要求或总体设计单位提出的要求进行计算。时域分析法能够较全面准确地模拟冲击过程。

抗冲击设计一般通过隔振器自身的抗冲击设计或在隔振系统中加装限位器来实现。如何在主被动混合隔振系统中进行抗冲击设计一直以来是主动控制领域的难题。英国的智能弹簧技术[4]为了实现抗冲击性能将电磁作动器的气隙设定很大，使其功耗增加。除此之外，隔振系统限位器的参数如果选取不合理，可能会使隔振系统的最大加速度过大，造成二次冲击。文献[5-7]通过理论和有限元的方法对隔振系统中的限位器进行了分析研究，并提出了限位器参数设计的原则。

本文针对提高电磁-气囊主被动混合隔振系统的抗冲击特性，首先对电磁-气囊主被动混合隔振器抗冲击设计进行理论推导，建立其动力学模型进行了仿真，并通过试验进行验证。然后推导混合隔振系统中限位器的理论模型，研究主被动混合隔振系统在冲击载荷下，限位器对冲击响应的影响。研究成果可为主被动混合隔振系统的抗冲击设计提供参考。

1 混合隔振器抗冲击设计

1.1 抗冲击悬挂结构设计

电磁-气囊主被动混合隔振器是将电磁作动器集成至气囊隔振器中，由气囊承载被隔振设备重量的同时进行宽频隔振，电磁作动器输出主动控制力进行线谱控制[8]，其结构如图1 所示。作动器为单边永磁偏置型，主要由铁芯、衔铁、线圈、永磁体和填充在气隙中的导磁橡胶组成。若混合隔振器不进行抗冲击设计，在遭遇恶劣工况时容易使电磁作动器损坏，影响其可靠性。为了增强混合隔振器的抗冲击性能，本文设计了混合隔振器的抗冲击悬挂结构，该结构主要由与气囊上盖板固定的上座和与衔铁连接的下座组成。其中下座与上座通过抗冲击弹簧的预紧力接触，其中预紧力主要包括上下座之间的摩擦力和作动器偏置力对下座的吸引力。当正常工作时，悬挂结构不工作，下座与上座接触；当受到冲击载荷时，上座与下座脱开，抗冲击弹簧工作，在避免气囊隔振器刚性短路的同时，也保护了电磁作动器免受损坏。设气囊的刚度为ks，电磁作动器的负刚度为ka，导磁橡胶刚度为km，抗冲击弹簧的刚度为kb，当正常工况时，隔振器的刚度可表示为

在冲击工况下，当悬挂结构脱开时，隔振器的刚度可表示为

由于抗冲击弹簧的刚度较小，隔振器的刚度又可近似表示为

由式（3）可得，在混合隔振器遭受冲击载荷时，悬挂结构脱开后，混合隔振器的刚度变化不大，在避免混合隔振器丧失隔振性能的同时也保护了电磁作动器免受损坏，当冲击载荷消失后，悬挂结构又可复位，增强了混合隔振器的稳定性和适应性。

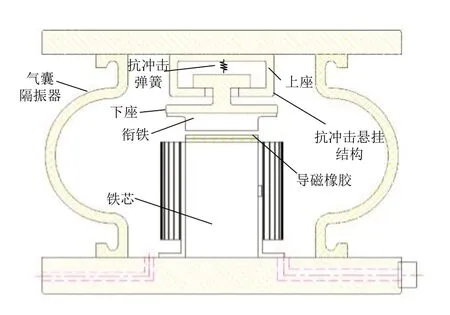
图1 电磁-气囊主被动混合隔振器结构图 Fig.1 Active-passive hybrid vibration isolation of electromagnetic actuator and air spring

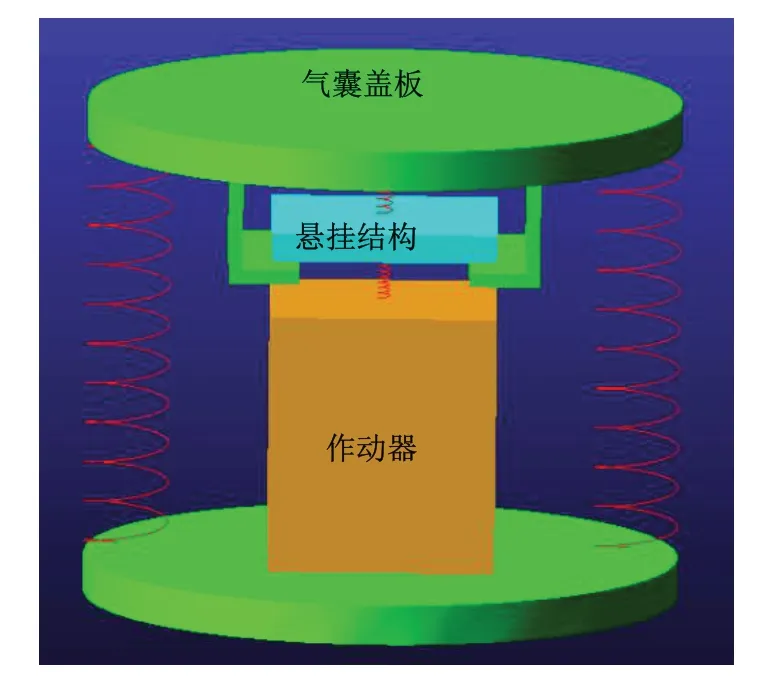
图2 混合隔振器抗冲击悬挂结构多刚体动力学模型Fig.2 The multi-rigid-body dynamic model of anti-shocksuspended structure of hybrid isolator

1.2 抗冲击结构静态特性计算

悬挂结构的设计由抗冲击弹簧的刚度kb、导磁橡胶刚度km和预紧力的大小等参数决定。由于悬挂结构脱开阶段涉及电磁力和摩擦力的变化，通过理论计算很难准确获得其特性。本文建立了悬挂结构的多刚体动力学模型，如图2所示。通过建立悬挂结构的多刚体动力学模型，可以很好地研究抗冲击弹簧的刚度kb、导磁橡胶刚度km、预紧力的大小等性能参数对悬挂结构的影响，进而对悬挂结构进行优化设计。

设隔振器的刚度ka为250 N/mm，导磁橡胶的刚度km为5 000 N/mm，将衔铁与导磁橡胶之间的空气间隙设为1 mm，保持抗冲击弹簧的刚度kb为200 N/mm 不变，通过位移控制实现气囊上盖板以0.1 mm/s的速度缓慢向下移动，计算预紧力分别为100 N、200 N和300 N时的力-位移曲线，采集气囊上盖板所受的总力，仿真结果如图3 所示。保持预紧力为200 N 不变，计算当抗冲击弹簧的刚度分别为100 N/mm、200 N/mm和300 N/mm时的力-位移曲线，结果如图4所示。由图3和图4的计算结果可得，当衔铁与导磁橡胶未接触时，此时曲线的刚度为250 N/mm；当衔铁与导磁橡胶接触时，此时刚度迅速增大，随着预紧力的增大，隔振器脱开所需要的位移也越大，此时隔振器的刚度约为2 500 N/mm；当悬挂结构脱开后，由图3 可得此时的隔振器刚度约为436 N/mm，且刚度不随着预紧力的变化而变化，约为抗冲击弹簧与隔振器的刚度之和。由图4可得隔振器的刚度随着抗冲击弹簧刚度的增加而增加，当抗冲击弹簧的刚度分别为100 N/mm、200 N/mm 和300 N/mm 时，悬挂结构脱开后隔振器的刚度分别为346 N/mm、436 N/mm、522 N/mm，与理论分析相符。保持抗冲击弹簧的刚度为200 N/mm，预紧力为200 N，将导磁橡胶的刚度设为2 500 N/mm、5 000 N/mm，、7 500 N/mm 和趋近于无穷大，计算结果如图5所示。由图可得，随着导磁橡胶刚度的增大，在脱开阶段隔振器的刚度也越大，这是由于导磁橡胶与衔铁接触时，首先需要克服预紧力之后，抗冲击弹簧才会发挥作用，导磁橡胶的刚度越大，在此阶段隔振器的刚度也越大。因此为了避免隔振器在脱开过程中刚度过大，在考虑导磁橡胶本身的导磁性能外，应选用刚度较小的材料进行设计加工。

对所研制的承载力为1 t，主动输出力为80 N的混合隔振器进行抗冲击设计时，选用刚度为200 N/mm的抗冲击弹簧。通过MTS试验机调整混合隔振器的高度，使衔铁与导磁橡胶的距离为1 mm，然后向气囊内充气，使其承载力大约为8.8 kN。在试验过程中采用位移方式控制，以0.05 mm/s的加载速度缓慢下压，试验结果如图6所示。由图中拟合曲线方程可得，在衔铁与导磁橡胶接触之前，刚度为250 N/mm，此时为气囊隔振器的刚度值；当衔铁与导磁橡胶接触后，悬挂结构未脱开前，刚度为3 500 N/mm；当悬挂结构脱开后，隔振器刚度迅速减小为690 N/mm，这时的刚度与气囊的刚度与抗冲击弹簧的刚度之和偏大，可能是由于隔振器内部悬挂结构装配之间的摩擦力等因素造成的。试验中刚度曲线的趋势与仿真结果相仿，悬挂结构的设计避免了混合隔振器在大位移工况下的隔振失效，满足舰船对冲击摇摆性能的要求。

图3 不同预紧力下混合隔振器的位移-力曲线 Fig.3 The displacement-load curve under different pretightening forces

图4 不同刚度下混合隔振器的位移-力曲线Fig.4 The displacement-load curve under different stiffnesses of hybrid isolator

图5 不同的导磁橡胶刚度下混合隔振器的位移-力曲线 Fig.5 The displacement-load curve of hybrid isolator under different stiffnesses of magnetic conductive rubber

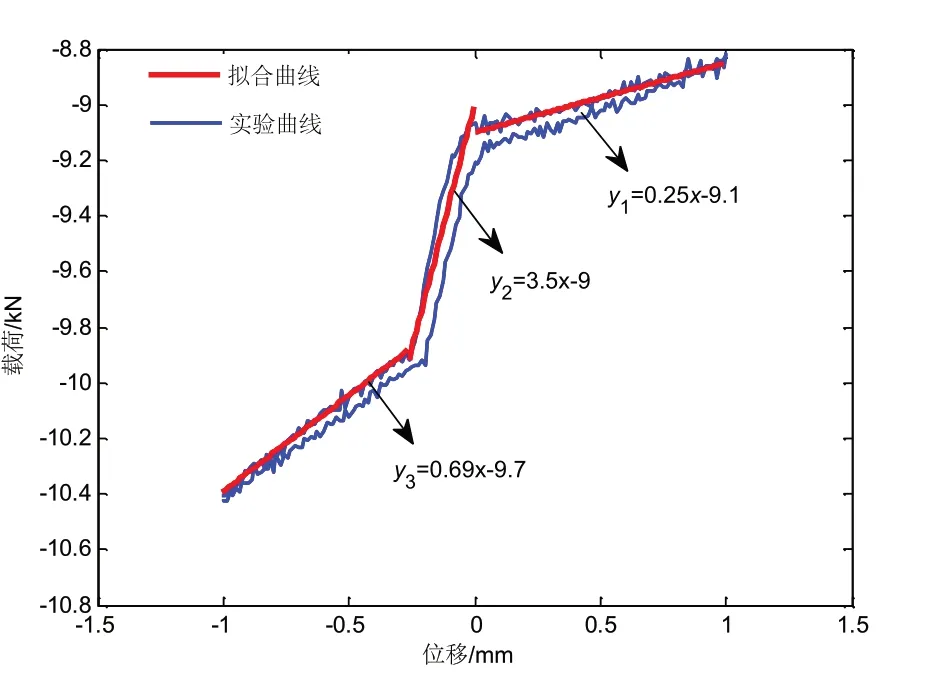
图6 混合隔振器位移载荷曲线Fig.6 The load-displacement curve of active-passive hybrid vibration isolator

2 混合隔振系统限位器设计

2.1 限位器设计理论

在主被动混合隔振系统中，除了隔振器本身的抗冲击性能外，还需要安装限位装置来防止设备的最大位移过大。设限位器的刚度为kr，其结构原理图如图7所示。当隔振器变形x ＜Δx 时，限位器不起作用，此时隔振系统的刚度为混合隔振器的刚度k；当隔振器变形x ＞Δx 时，限位器发生接触，此时隔振系统的刚度为k + kr。

设冲击的初始速度为v0，当限位器不工作时可得设备的最大响应位移和最大加速度为[4]：

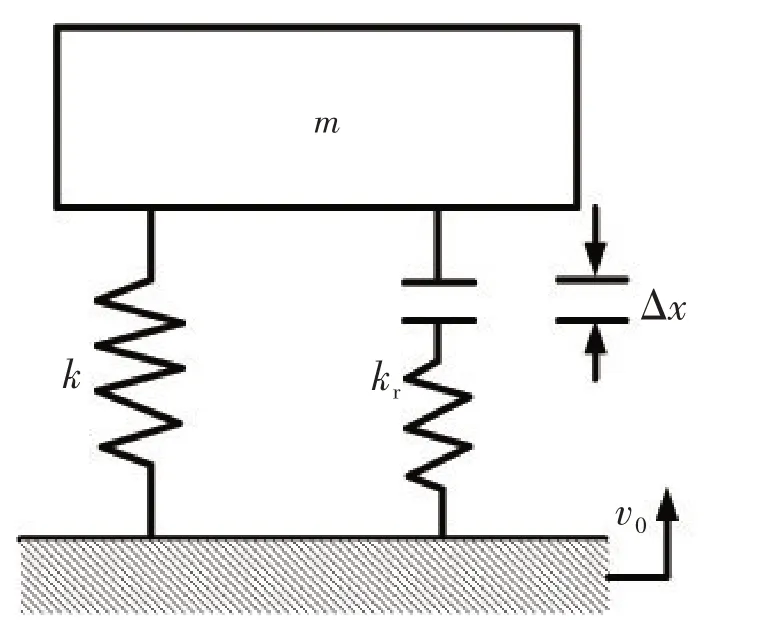
图7 主被动混合隔振系统中限位器结构原理Fig.7 The theoretical model of restrictors in active-passive isolation system

当系统遭受冲击载荷时，由于冲击载荷作用时间短而忽略阻尼和冲击过程中的能量损耗，由能量守恒定律可得

解得

由式（6）与式（7）可得，限位器作用下隔振系统冲击响应与隔振器的刚度k、限位器的刚度kr和限位器的间隙Δx 有关。通过文献[5]可得，隔振系统的冲击响应最大位移与限位器的刚度成反比，最大加速度与限位器的刚度成正比；当限位器的间隙增大时，最大加速度会减小，但同时最大位移会增大。在主被动混合隔振系统中，当隔振器与电磁作动器选型后，根据整个隔振系统的需要确定其最大允许位移、最大允许加速度，这时限位器的设计对提升系统的抗冲击能力至关重要。通过搭建主被动混合隔振系统的多刚体动力学模型，可以对限位器进行研究，为限位器的设计与选型提供指导。

2.2 多刚体动力学建模

利用计算机软件在隔振系统的设计阶段进行计算和测试，能够使隔振系统最大可能地满足设计目标。本文通过ADAMS 软件建立了主被动混合隔振系统多刚体动力学模型，在冲击载荷下，分别研究了限位器性能参数和隔振器性能参数对系统响应的影响。图8 为柴发机组主被动混合隔振系统三维模型。该系统主要由柴油发电机组、筏架、6 个主被动混合隔振器、基座组成。柴发机组用等效质量来代替。筏架、基座模型由SolidWorks 建模后导入至ADAMS软件中，进行质量等参数的设置。模型中用弹簧代替电磁-气囊主被动混合隔振器。通过ADAMS 中的运行过程函数可以对隔振系统的加速度、位移和传递力等参数进行提取。主被动混合隔振系统的具体参数为：上层质量块的质量为3.4 t，筏架的质量约为1.65 t，基座的质量约为1.56 t。筏架与基座之间弹簧的静刚度为250 N/mm，动刚度为350 N/mm。

限位器在正常工况下不会起作用，在冲击摇摆工况下，当设备位移达到一定值时，限位器会发生接触、碰撞，起到限位的作用。在ADAMS中定义两个物体发生接触时，单边接触可以用单边冲击函数Impact 来实现，双边接触可以用双边冲击函数Bistop 来实现[9]。在本节分析中，主要考虑上下限位，不考虑左右限位，故选用双边冲击函数Bistop。

图8 主被动混合隔振系统多刚体动力学模型Fig.8 Virtual prototype of passive-active hybrid isolation system

2.3 冲击载荷确定

对所搭建的主被动混合隔振系统模型进行抗冲击计算能够更好地了解系统的抗冲击能力，在计算时，将激励垂向施加在基座上，并计算隔振器和设备的位移量。根据GJB 1060.1-91相关规定[10]，设计加速度a0与设计速度V0可由式（8）和式（9）计算得出。

图9 基座横向与垂向冲击加速度时域图Fig.9 Time domain diagram of vertical and transverse shock acceleration on base

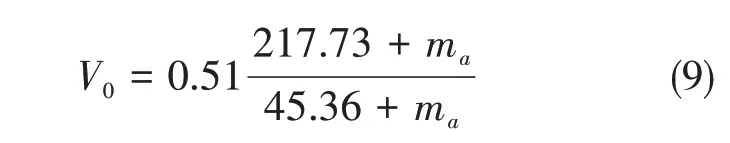
式中，垂向和横向的设计加速度与设计速度分别为a0与V0，纵向的设计加速度与设计速度分别为0.4a0与0.4V0。本节以计算垂向冲击为例，对所建模型进行垂向冲击的校核与计算。

通过德国BV043-85 标准[11]可将冲击谱简化为三角形变化历程或正弦变化历程进行验证计算。本文采用三角形变化历程。设冲击过程中的位移谱为10 mm，输入三角形冲击时域谱如图9 所示。其中正半三角波加速度大小为63.01 m/s2，半正三角波脉宽为0.012 4 s，负半三角波加速度大小为20.79 m/s2，负半三角波脉宽为0.037 7 s。

2.4 限位器参数对冲击响应的影响

（1）限位器间隙对抗冲击性能的影响

为了研究限位器间隙对隔振系统的最大相对位移和最大绝对加速度的影响，设限位器的刚度为1.6×104N/mm，阻尼为50 N⋅s/mm，分别计算限位器间隙为4 mm、5 mm、6 mm和无限位器时，在冲击载荷下的响应。计算结果如图10-13 所示。由图10 和图12 可得，随着限位器位移间隙的增大，隔振系统最大相对位移会随之增大，当不安装限位器时的响应位移最大，当限位器间隙为4 mm时，隔振系统的最大位移为7.242 mm，当不安装限位器时，隔振系统的最大位移为9.25 mm。同时由图可得，随着限位器间隙的变大，相对位移达到最大幅值所用的时间也越久。图11所示为隔振系统绝对加速度随限位器间隙变化的时域图，图13 为最大绝对加速度随限位器位移间隙变化的曲线。由图可得，随着限位器间隙变小，隔振系统的绝对加速度不断变大。所以在限位器选型过程中，在考虑限制隔振系统的最大位移的同时，还应该避免限位器在冲击工况下产生过大的冲击力。

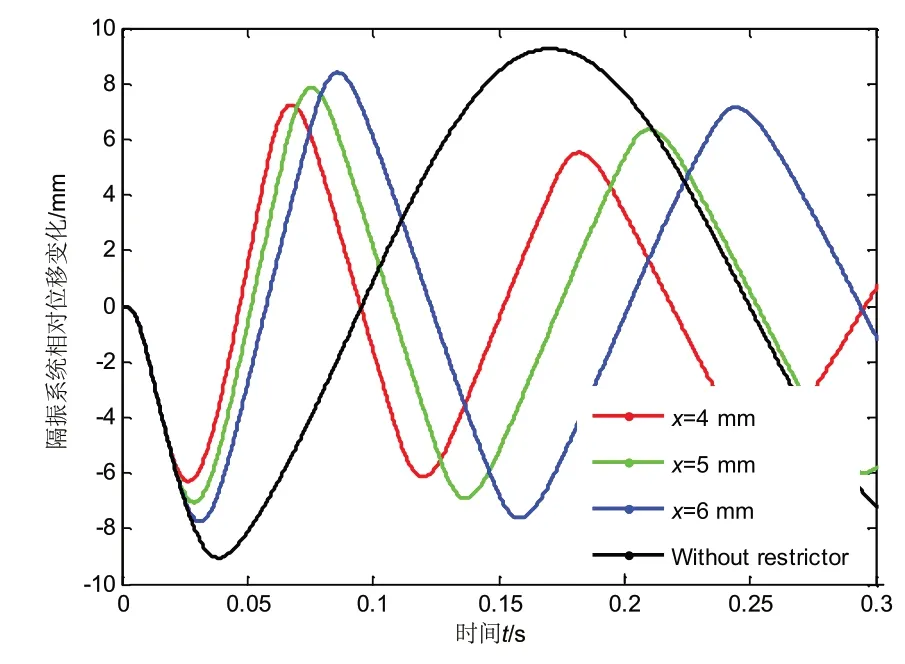
图10 隔振系统相对位移时域图 Fig.10 The time series of relative displacement of isolation system

图11 隔振系统绝对加速度时域图Fig.11 The time series of absolute acceleration of isolation system

（2）限位器刚度对抗冲击性能的影响

由上面分析可知，限位器的间隙对隔振系统的绝对加速度与相对位移影响很大，且当限位器间隙较小时，隔振系统的绝对加速度会急剧增大，因此选用弹性限位器就至关重要。在搭建的混合隔振器多刚体动力学模型中，可以通过改变限位器的刚度，方便地得到系统的绝对加速度与相对位移的变化情况。将限位器间隙设定为5 mm，分别计算限位器刚度为1.3×104N/mm、1.6×104N/mm、1.9×104N/mm、2.1×104N/mm、2.4×104N/mm 和2.7×104N/mm 时隔振系统的冲击响应。计算结果如图14和图15所示。由图14 可得，当限位器位移间隙设定不变时，隔振系统在冲击载荷下最大相对位移随着隔振器刚度的增加而减小。与此同时，由图15 可得，隔振系统的最大绝对加速度会随之增大。所以在对限位器选型时，应综合考虑主被动混合隔振系统能够承受的最大位移与最大加速度，提高系统的抗冲击能力。

图12 隔振系统最大相对位移 Fig.12 The maximum relative displacement of isolation system

图13 隔振系统最大绝对加速度Fig.13 The maximum absolute acceleration of isolation system

图14 隔振系统最大相对位移 Fig.14 The maximum relative displacement of isolation system

图15 隔振系统最大绝对加速度Fig.15 The maximum absolute acceleration of isolation system

3 结 语

本文探讨了电磁-气囊主被动混合隔振器的抗冲击设计，首先提出了抗冲击悬挂结构的设计，并对其进行了理论建模、仿真，得出了各结构参数对隔振器力-位移曲线的影响，设计过程中应选用刚度较小的抗冲击弹簧和导磁橡胶，同时为了避免悬挂结构脱开所需位移过大，也应使预紧力尽量小。本文所设计的抗冲击悬挂结构测试结果表明，可以避免混合隔振器在大位移工况下的隔振失效，满足舰船对冲击摇摆性能的要求。在此基础上建立了隔振系统中限位器的理论模型，通过建立隔振系统的多刚体动力学模型，分析了限位器的参数对系统最大相对位移和最大绝对加速度的影响规律。由理论和仿真结果可知，限位器减小混合隔振系统最大相对位移是建立在增大其最大绝对加速度的基础上的。所得的规律可以应用于主被动混合隔振系统限位器的理论设计，主要用来确定限位器工作间隙和刚度，使混合隔振系统在冲击响应下最大相对位移和最大绝对加速度都在设计要求范围内。