简化双层底结构振动传递及抑制特性分析

陈美霞，陈 琦

（华中科技大学船舶与海洋工程学院，武汉430074）

0 引 言

我国正在建设“蓝水海军”，走向深蓝，舰船结构振动所引起的一系列问题越来越受到关注。双层底是舰船上常见的一种结构，内外底之间通过底纵桁等构件连接。内底上由动力设备激起的振动会通过底纵桁传递至外底，由此向水中产生的声辐射会显著降低舰船的隐身性和战斗力。近几十年来，美、俄等国都已实现舰船低噪声化，舱室振动环境也得到了极大的改善。我国舰船结构声学优化设计与当前国际先进水平还存在着相当大的差距。

船体结构由一系列金属构件焊接而成，在进行理论研究时，这些结构可以简化成“L”、“T”、“十”字型等。当振动波经过这些不连续转角结构时，不仅波形会发生转换，振动能量也会发生透射和反射[1-2]。为阐明振动传递机理，研究人员通常将这些结构简化成半无限长。车驰东[3]研究了半无限长单转角结构的振动能量透射及反射率并分析了转角角度和板厚比对不同波形振动能量传递的影响。姚熊亮等[4]运用波分析法研究了半无限长不同形式转角结构中的弯曲波能量衰减，并给出隔声量工程预报公式。对于舰船的双层结构，根据姚熊亮等[5]的研究，水层的耦合作用随频率的增高而降低，托板的耦合作用随着频率的增高而增加，托板在内、外壳的振动传递中起较大作用，阻尼托板结构在中高频能有效地抑制结构声能量的传递。Cremer等[6]在其关于结构声的经典著作中提出了阻振质量的概念，阻振质量可以将部分振动能量反射回振源，其作为阻波手段也得到了广泛的关注。车驰东等[7]运用波分析法研究了附加在单转角处的阻振质量对振动能量传递的阻挡作用，发现阻振质量对平面弯曲波透射所起的作用类似于一个“低通滤波器”。梁德利等[8]在双层壳舷间结构声传递途径试验分析基础上，提出了阻振质量复合托板结构，结果表明阻振质量复合托板显著降低了舱段中高频的振动及声辐射。作为刚性阻波手段的阻振质量对振动能起到很好的隔离作用，但其本身并不能消耗振动能量，且单独使用阻振质量会大大增加结构重量，采用复合阻波手段便成了一种选择。孙谦等[9]结合阻振质量与阻尼材料抑振降噪机理，基于数值方法给出了高传递损失托板的结构形式，有效地抑制了外壳的振动及声辐射。

为进一步分析双层结构振动传递及抑制特性，本文在上述研究的基础上，运用波分析法研究了阻振质量和阻尼层对弯曲波入射下简化双层底结构振动能量传递的抑制作用，以探索阻振质量结合阻尼层在复杂结构中应用的可能性。

1 理论分析

1.1 透射系数及反射系数

简化双层底结构由内外底板和底纵桁构成，其中内外底板1、2、4、5 为半无限长，底纵桁板3 为有限长，如图1～2所示，取z方向与各板宽度方向一致，建立原点分别在两个转角上的局部坐标系。

图1 波形转换 Fig.1 Conversion of wave type

图2 局部坐标系及受力示意图Fig.2 Local coordinate system and force analysis

考虑沿x1正方向传递的平面弯曲波由无穷远处向第一转角法向入射的情况。满足薄板弯曲方程的入射波横向振动速度可以表示为

式中，vIB为入射弯曲波幅值。为简化计算，接下来与时间变化相关的简谐因子ejωt均略去，只保留空间变化项。行波在传递过程中会发生透射及反射，在转角处还会产生近场波。

1.1.1 各板的振动方程

（1）板1的横向及纵向质点振速（x1＜0）

（2）板2的横向及纵向质点振速（x1＞0）

（3）板3的横向及纵向质点振速（x2＞0）

（4）板4的横向及纵向质点振速（x3＜0）

（5）板5的横向及纵向质点振速（x3＞0）

1.1.2 第一转角处耦合方程

（1）速度及角速度连续性

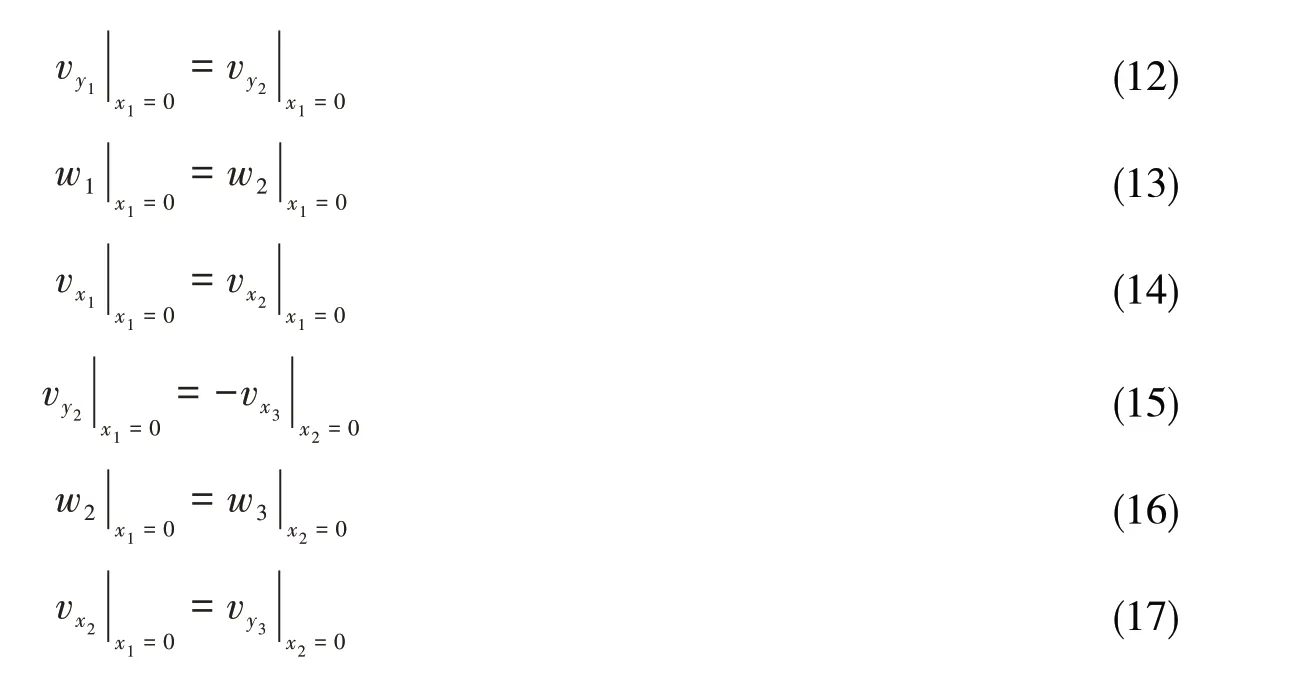
（2）力与力矩平衡

1.1.3 第二转角处耦合方程

（1）速度及角速度连续性

（2）力与力矩平衡

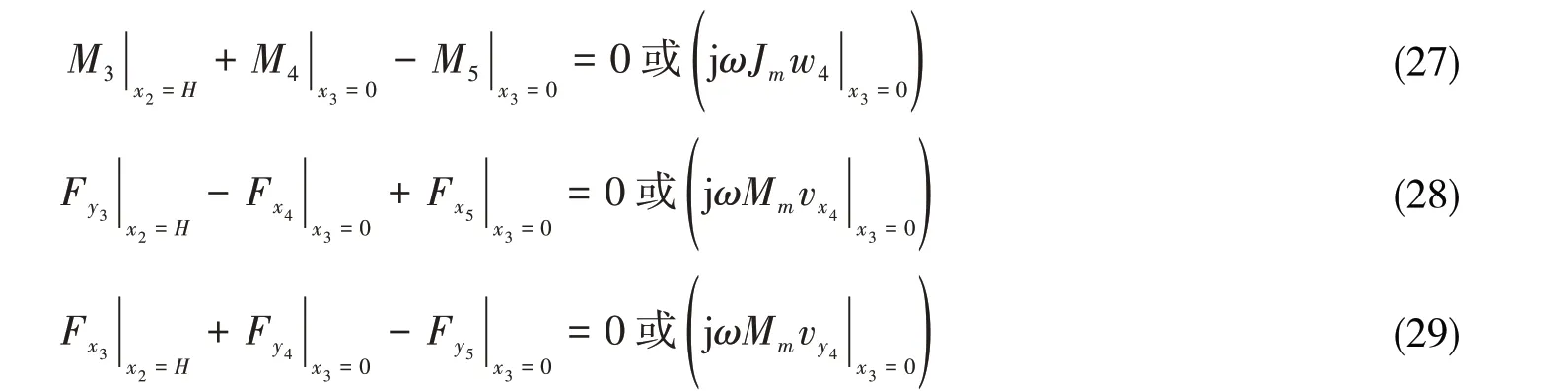
上式中，kBi和kLi分别为弯曲波和纵波波数，Fxi为正应力，Fyi为剪应力，Mi为弯矩，wi是角速度（i =1，2，3，4，5）。转角处附加阻振质量时，力与力矩平衡式右边写成括号内形式，其中Mm为阻振质量单位长度质量，Jm为其转动惯量。

内力与振速存在以下关系：

式中，B = EI/( )1 - μ2为平板的弯曲刚度，E 为弹性模量，μ 为泊松比，I = h3/12 为板单位宽度的截面惯性矩，cL是平面纵波波速，m'= ρh为板单位面积的质量。将转角处18个耦合方程写成矩阵形式得

式中，X =( rBB1rBj1rBL1tBB2tBj2tBL2,…,tBB5tBj5tBL5)T是待求解振速透射及反射系数向量，A 是系数矩阵，F是入射弯曲波引起的非齐次项。

若考虑结构的阻尼，则相应板中的弯曲波和纵波波数应该写成

式中，η为结构损耗因子，采用考虑基底层阻尼的自由阻尼结构损耗因子[10]：

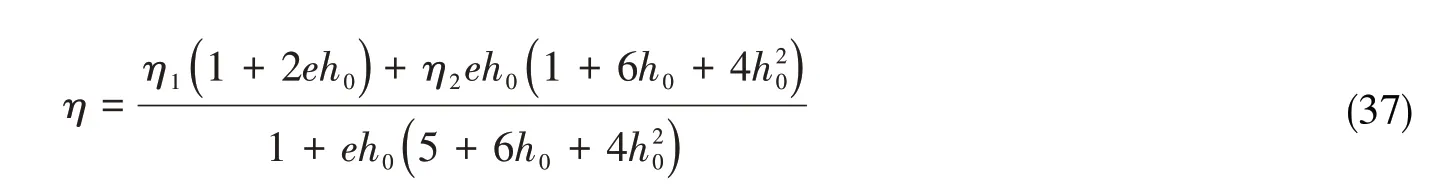
其中，η1、η2分别为基底层和阻尼层材料的损耗因子，e = E2/E1、h0= h2/h1分别为阻尼层和基底层材料的杨氏模量与板厚比。

以上推导基于Poisson-Kirchhoff 薄板假设，即弯曲波波长和板厚之间必须满足λB＞6h，这就为分析设定了频率上限[6]：

对于频率高于式（38）的情况，必须考虑板内剪切，采用Mindlin 厚板理论对公式进行修正。船用钢板在绝大部分情况下都能满足薄板假设，例如对于20 mm 厚的钢板（大约为船体外板厚度），可得fmax= 13.5 kHz，这个频率上限足以满足一般情况下对结构振动分析的要求。

1.2 能量传递效率

在某一固定频率下，平面弯曲波及纵波的能量流与振速的关系为

式中，cB和cL分别为平面弯曲波和纵波波速，则入射波能流密度为

为了研究各类透射及反射波所携带的振动能量占入射波能量的比例，提出了以下能量透射及反射效率：

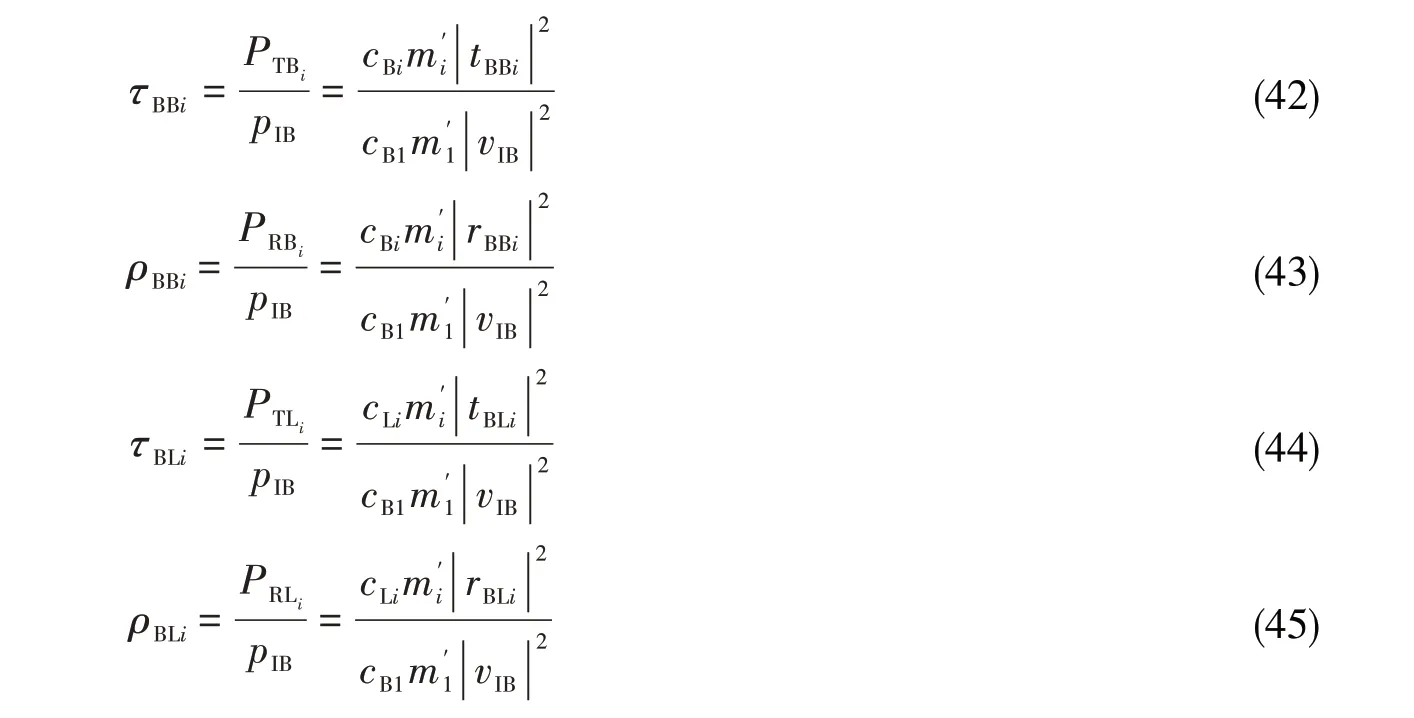
式中，P 表示能流密度，下标B、L 分别表示弯曲波和纵波，I、R、T 分别表示入射、反射和透射。由于转角处不能储存或耗散振动能量，在不考虑阻尼的情况下，根据能量守恒原理，以上能量透射及反射效率应当满足

各板对弯曲波的传递损失定义为

2 数值分析

2.1 双层底结构振动传递特性

取板厚均为h1= 20 mm 的钢板组构成简化双层底结构,钢板材料密度ρ1= 7.8×103kg/m3，杨氏模量E1= 2.1×1011N/m2，泊松比μ1= 0.3，损耗因子η1= 0.01，底纵桁高H=1 m，计算能量透射及反射效率如图3-4所示。

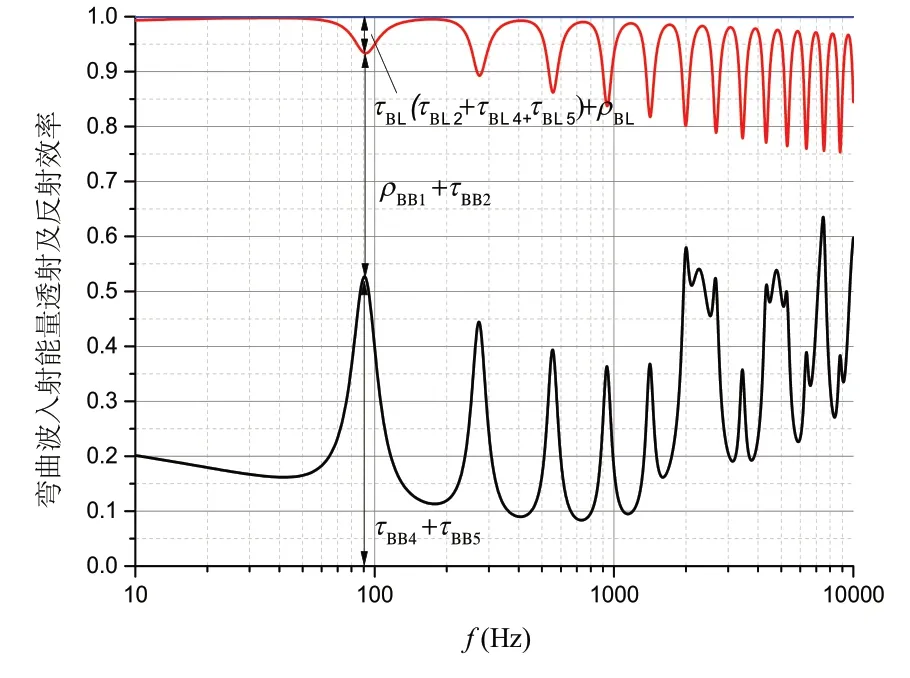
图3 透射及反射效率 Fig.3 Transmission and reflection efficiency

图4 板3净透射效率Fig.4 Net transmission efficiency of Plate 3

由图3-4分析可知：

（1）在计算频率范围内，全部透射及反射效率之和等于1，说明根据理论分析计算的结果满足能量守恒关系。波动形式发生转变的振动波能量ρBL+ τBL占入射波能量比例虽然随着频率的增加呈增大趋势，但总体所占比例较小，内外底板依然以弯曲振动为主。

（2）忽略外底板纵向振动，外底板弯曲波能量流τBB4+ τBB5和板3 沿着x2正方向净能量流τBB3+τBL3曲线变化趋势一致，大小也几乎相同，呈现出一定的波动特性。这是因为板3 正方向净能量流由τBB3和τBL3叠加而成，它们的峰值分别出现在板3各阶弯曲和纵向振动固有频率处，这也正是外板能量流极大值对应的频率附近；当板3 发生弯曲或者纵向反向共振时，外板能流出现极小值，对应于图中的波谷频率处。

2.2 双层底结构振动抑制特性

如图5所示，在转角处附加100 mm×100 mm的阻振质量，板3上附加厚h2=6 mm，材料损耗因子η2=0.8，密度ρ2=3×103kg/m3，杨氏模量E2=7.8×1010N/m2，泊松比μ2=0.5的阻尼层，考察以下几种阻振方案。

图5 附加阻振措施模型 Fig.5 Model with blocking mass and damping layer

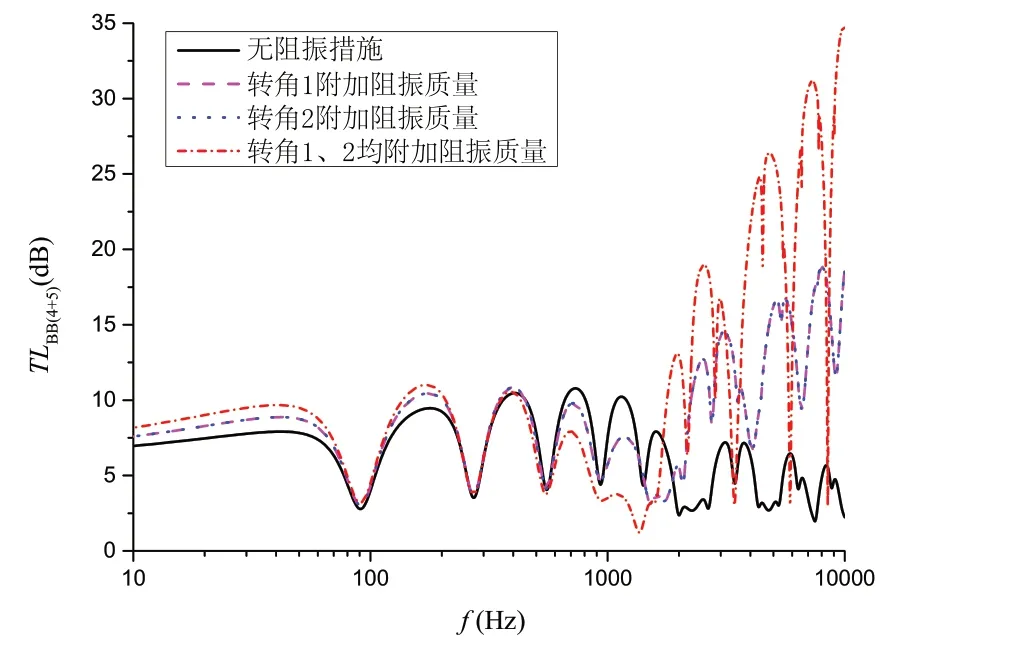
图6 不同阻振质量布置下传递损失F ig.6 Transmission loss of different blocking mass arrangements

从图6可以看出：

（1）无论是否附加阻振质量，传递损失随频率均在一系列极大值与极小值之间波动。在不附加阻振质量下的某些频率，板3 发生反向共振，从而使得传递损失在该频率附近达到极大值；但在附加阻振质量后，反向共振的相位平衡被打破，使得传递损失有所减小，这种情况下应避免使用阻振质量；

（2）从总体上看，在中低频，阻振质量对传递损失几乎没有影响；但在高频，附加阻振质量后的传递损失要明显高于无附加阻振质量的情况；单阻振质量附加在第一转角与附加在第二转角的传递损失几乎相同。双阻振质量对双层底结构中高频振动传递的抑制作用，以及其在板3 的共振及反向共振频率附近对振动传递的影响均要大于附加单阻振质量情况。

从以上分析可知，在中低频，在多转角附加多级阻振质量并不能明显起到阻振效果，甚至在中高频的某些频率下显著减小传递损失。考虑阻振质量结合阻尼层的复合阻振方式，不同工况下的传递损失如图7所示。

由图7中各曲线比较可得：

（1）在中低频，复合阻振方式和单独使用阻尼层对振动传递的抑制几乎相同，但在高频能够取得更好的减振效果；

（2）在中低频，复合阻振方式和单阻振质量传递损失曲线变化趋势一致，但在峰值处，前者能显著地提高传递损失；在高频，复合阻振方式则完全优于单阻振质量。这是因为附加在转角2 的阻振质量能够将原本传到外底板的振动能量反射回板3，让阻尼层更有效地吸收；

（3）复合阻振方式对振动传递的抑制有比多转角附加多级阻振质量更好的效果，不仅可以有效地拓宽隔振频带，而且可以在板3固有频率（尤其是高频）附近避免共振带来的较低传递损失情况。

图7 阻振质量结合阻尼层传递损失Fig.7 Transmission loss by combining blocking mass and damping layer

3 数值验证

为使用FEM 验证以上理论分析的正确性，在ANSYS 中建模时须对理论模型进行截断，采用阻抗边界模拟理论模型中的无反射边界。截断边界处阻尼器y 向阻尼系数为平面弯曲波特征剪力阻抗cBm'，x向阻尼系数为平面纵波特征力阻抗cLm'，绕z轴扭转阻尼系数为平面弯曲波特征弯矩阻抗B/cB。

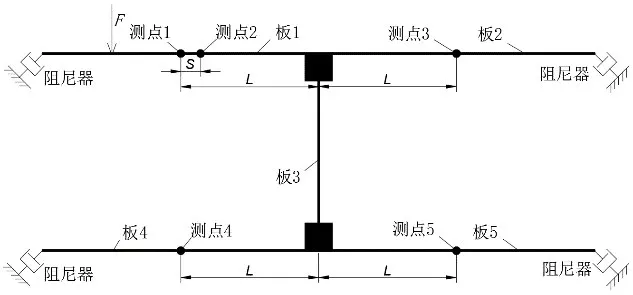
图8 无反射边界和测点 Fig.8 Non-reflection boundary and measuring points

图9 双层底有限元模型Fig.9 FEM model of double bottom

有限元模型中激励力、测点、以及阻抗边界如图8-9所示。距离L大于2倍近场波波长时，可忽略近场波的影响，此时测点1、2 附近区域只需考虑入射波与反射波，测点3 附近只有透射波。设到达第一转角处的入射波为wIe-jkx，反射波为wRejkx，测点1、2的距离为S，则测点1、2、3的横向位移分别为

根据测点位移求解反射系数、透射系数和相应的传递损失为

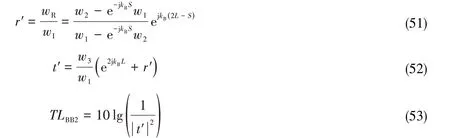
同理，根据测点4和5的数据，可求出弯曲波传递损失TLBB4与TLBB5。

图10 传递损失比较（无阻振质量）Fig.10 Comparison of transmission loss(without blocking mass)

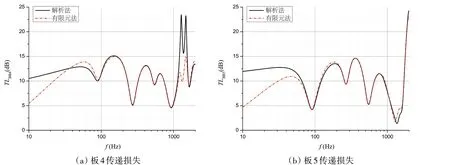
图11 传递损失比较（双阻振质量）Fig.11 Comparison of transmission loss(with blocking mass)

由图10～11中曲线对比可见：

（1）无论是否附加阻振质量，两种方法计算所得的传递损失基本吻合，验证了本文解析法与有限元法的正确性；

（2）由于低频弯曲波波长较长，有限元计算时所取L没有大于两倍弯曲波波长，受近场波影响，两条曲线在低频误差较大；此外受有限元网格大小的局限，在1 000 Hz 以上两条曲线也会出现一定误差，但变化趋势还是保持一致。

4 结 论

本文运用波分析法对弯曲波入射下简化双层底结构的振动能量传递与抑制问题进行了理论分析，并进行了数值实验，得出以下结论：

（1）理论计算和数值实验所得结果基本吻合，这证明了理论分析的正确性，同时说明阻抗边界能有效模拟平面波法向入射时的无反射边界情况；

（2）当弯曲波从内底板入射时,内外底板的振动均以弯曲振动为主。当激励频率在底纵桁弯曲或纵向振动固有频率附近时，振动能量传递效率最大，外底板的弯曲振动最剧烈；

（3）在中低频，附加在转角处的阻振质量几乎起不到任何阻振作用，在高频则能起到明显的阻振作用，且布置数量越多阻振效果越好；但在某些频率下，阻振质量也会明显降低传递损失，起相反作用，此时应避免使用；

（4）阻振质量结合阻尼层的复合阻振方式能够显著提高抑制效果，有效拓宽隔振频带，不仅能避免某些频率下单独使用阻振质量过低传递损失情况出现，还能提高阻尼层的吸收效果，减轻结构重量，这对船体双层结构声学设计具有一定的指导意义。

本文通过对建立的简化模型理论分析初步得出一些结论，考虑到实船双层底结构的复杂性，仍需建立更复杂的模型进行深入研究。