旋转翼对海洋立管涡激振动抑振的数值研究

王 伟，宋保维，毛昭勇，田文龙，张婷颖

（1.西北工业大学航海学院,西安710072；2.无人水下运载技术工业和信息化部重点实验室,西安710072）

0 引 言

涡激振动是一种在海洋工程领域较为常见的流固耦合现象。当海洋立管受到海流作用时，在立管结构后方会产生脱落的漩涡，周期性脱落的旋涡使结构产生横向的脉动力，从而使结构发生周期性振动。尤其当涡脱落的频率处于结构振动的固有频率附近时，会发生频率锁定的现象，此时结构处于高振幅运动状态，易造成结构的疲劳损伤或直接破坏[1-2]。海洋立管结构易发生涡激振动，如何减小立管结构因涡激振动产生的疲劳损伤或破坏具有重要的工程意义[3]。

目前，常见的涡激振动控制方法分为主动控制和被动控制两大类[4]。文献[5]通过实验研究了粗糙带对结构涡激振动的抑制作用，振幅最优可以降低30%左右；文献[6]通过数值模拟研究了不同形状的整流罩对立管结构涡激振动的控制作用；文献[7]通过数值模拟研究了控制杆对立管涡激振动的抑振效果；文献[8]通过数值模拟研究了尾流分隔板对立管结构涡激振动的抑振作用，发现C型尾流板可以有效抑振。上述方式均为常见的被动控制方法，此类方法较为简单，但控制效果有限。不同于被动控制方法，主动控制方法需要额外的能量输入，但主动控制方法更为有效，且受外界因素的影响小。文献[9]通过实验研究了一种电制动器对立管结构涡激振动的控制作用；文献[10]通过实验研究了一种主动反馈控制方法对立管结构涡激振动的控制作用；文献[11]通过实验研究了表面吹吸对立管结构涡激振动的控制作用；文献[12]通过实验研究了壁面加热的方法。

旋转翼属于主动控制方法的一种，通过在立管结构上安装旋转的NASA 翼来达到抑振的目的。文献[13]和文献[14]分别通过数值模拟和实验方法研究了立管自身旋转的抑振效果，发现抑振效果较好。立管自身旋转在工程应用中存在较多的困难，而通过安装旋转翼来控制海洋立管的涡激振动存在很多优势：（1）NASA 翼是一种在航空领域应用广泛的低阻外形结构，旋转时阻力小，输入的能量也相对较小；（2）相较于其它主动控制方法，装置安装较为简单；（3）相较于被动控制方法，控制效果不受外界环境的影响，控制具有全向性。

本文提出了一种安装旋转翼来达到控制海洋立管涡激振动的方案，采用非定常数值计算方法对二维海洋立管涡激振动特性进行数值模拟。数值模型采用k-ω/SST 湍流模型，建立单自由度涡激振动模型，并采用Newmark-β法求解单自由度涡激振动方程。最后，详细讨论了旋转翼对海洋立管涡激振动的控制影响。

1 物理模型

1.1 旋转翼设计

旋转翼的翼型采用NASA0015 翼型，翼型的特征长度（h）为50 mm，NASA 翼具有低阻特性。立管的直径（D）为250 mm，旋转翼质心距离圆柱表面距离（G）为125 mm，旋转翼的数量为4，图1所示为模型示意图[15]。旋转角速度的计算参数设置如表1所示。

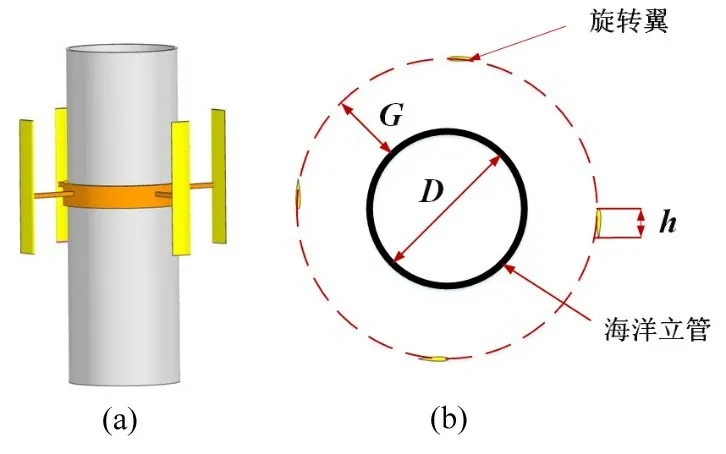
图1 安装旋转翼圆柱的示意图Fig.1 Diagram of marine riser with rotating wings

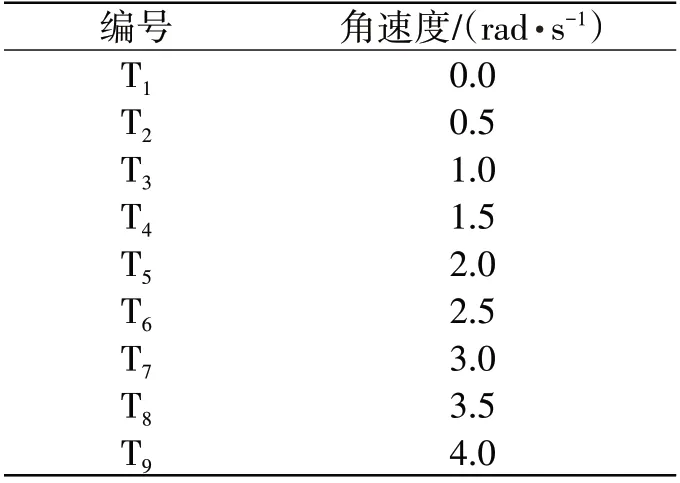
表1 计算参数的设置Tab.1 The setup of calculating parameters

1.2 涡激振动的表征参数

为便于分析和描述，定义与涡激振动相关的无量纲化表征参数如下：

雷诺数Re

阻力系数Cd

升力系数Cl

振幅比A*

频率比f*

约化速度Ur

式中：ρ为海水密度；U 为来流速度；μ 为动力粘性系数；Fx为立管所受阻力；Fy为立管所受升力；D 为立管的直径；S为立管迎来流方向的特征表面积，对于二维数值计算来说，S=D；A为立管的振幅；fs为立管涡脱落的频率；fn为立管的固有频率；ω为旋转翼旋转的角速度。

2 数值模型

2.1 单自由度涡激振动方程

立管结构单自由度涡激振动的物理模型可以简化为质量-弹簧-阻尼振动系统（如图2所示）。考虑竖向振动方程：

图2 涡激振动系统简化示意图Fig.2 Diagram of a simple VIV system

2.2 控制方程和湍流模型

不可压缩流动问题的求解控制方程主要为连续方程和Navier-Stokes方程，即

求解选用的湍流模型为k-ω SST 模型，该模型能够很好地处理近壁处低雷诺数的数值计算。该模型假设湍流黏度与湍流频率的关系为

湍流强度k满足

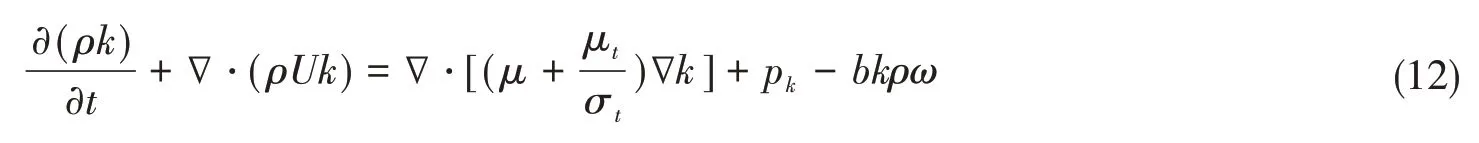
湍流频率ω满足

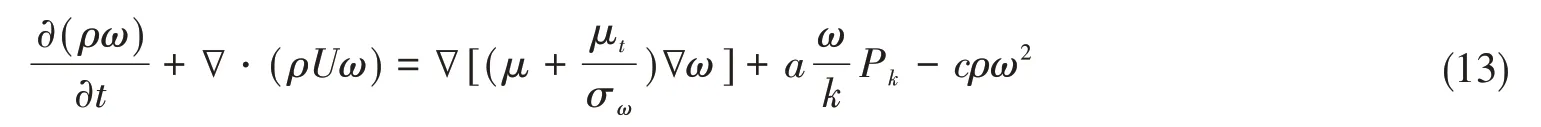
式中，a=5/9，b=0.09，c=0.075，σk=σω=2。

2.3 计算域和边界条件

在实际流体数值计算过程中，为了避免计算域过小或过窄导致的计算误差，将计算域设为40D×60D 的矩形区域，立管对计算域的阻塞度等于2.5%。海洋立管位于水平对称轴上，且距离入口边界为20D。计算域分为随体域、旋转域、振动域和外流场域。随体域为6D×6D 的正方形区域，其用于包裹立管和旋转域；旋转域用于包裹旋转翼；随体域和振动域之外的计算域均为外流场域（计算域示意图如图3所示）。

边界条件设置如下：（1）入口边界（inlet）为速度入口；（2）出口边界（outlet）为压力出口；（3）上下远场为对称边界（symmetry）；（4）海洋立管壁面（wall）为普通壁面；（5）随体域、旋转域、振动域和外流场域之间的交界边均设为interface。随体域、旋转域与立管壁面具有相同的振动运动规律；振动域为网格变形区域，网格变形采用铺层方法。

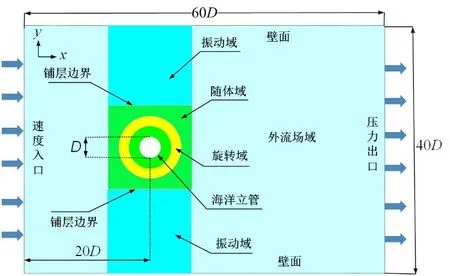
图3 计算域示意图Fig.3 Diagram of computational domain

2.4 网格划分

利用ANSYS ICEM CFD15.0对模型进行网格划分，为提高计算的精度，随体域和旋转域网格加密，且采用适应性较好的非结构化网格；振动域和外流场域采用结构化网格，网格较为稀疏，网格划分如图4所示。

图4 网格处理Fig.4 Mesh generation

数值计算的压力-速度耦合采用Couple 算法；模拟求解的格式均为精度较高的二阶迎风格式；控制方程的离散格式为Standard方法。残差收敛标准均设为1×10-5；计算步数为15 000步。立管结构和流场的耦合作用通过Fluent中的动网格技术来实现，立管结构所受流体力由Fluent中的流体数值算法求解；振动微分方程采用Newmark-β法求解；网格运动的速度和位移由Fluent 提供的宏访问更新。

3 数值模型验证

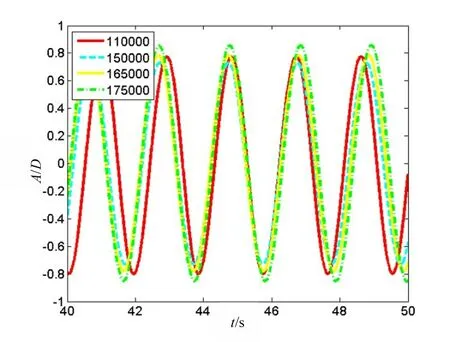
图5 网格无关性验证Fig.5 Results of the grid verification

网格会影响数值计算结果，因此有必要进行网格无关性验证。改变圆柱体结构表面的网格节点数和第一层网格的高度使得网格数分别为110 000、150 000、165 000 和175 000。图5 所示为不同网格数量下立管结构涡激振动的振幅比曲线，计算条件为Re=100 000（Ur=4.0）。由图可知：网格数为165 000 和175 000 的圆柱体在振幅稳定后，结果相差不大。因此可以认为当网格数大于175 000 时，网格尺寸基本不会对计算结果产生影响。

为确保数值模型的精确性，有必要进行实验验证。计算条件与文献[17]中的实验条件相同，计算的约化速度范围为2～14。计算结果同文献[17]中的实验结果以及文献[18]中的数值结果进行比对，对比结果如图6 所示。由图可知，本文数值模型计算结果的变化趋势与实验结果的变化趋势基本相同，建立的数值模型可以较准确地预测立管结构涡激振动的振幅特性和频率特性。

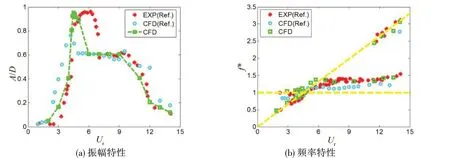
图6 数据对比Fig.6 Comparison of the characteristic results

4 计算结果与分析

4.1 旋转角速度对立管结构涡激振动抑振的影响

由图6 可知，当约化速度Ur=4.5 左右时，立管结构处于高振幅响应状态，以该约化速度为计算条件，对比分析T1～T9 立管的涡激振动响应。图7 所示为海洋立管涡激振动响应与旋转翼旋转角速度的关系（Ur=4.5），由图可知：（1）随着旋转翼旋转角速度的增加，立管的振幅比逐渐减小，最后基本不变；当ω=3.0 rad/s 时，振幅比接近于0，抑制振动效果十分明显；（2）随着旋转翼旋转角速度的增加，立管涡脱落的频率比先减小，后趋于不变；当旋转角速度大于2.0 rad/s 时，频率比开始迅速下降；当ω=3.0 rad/s时，频率比接近于0，抑制涡脱落的效果十分显著；（3）当ω=3.0 rad/s时，海洋立管涡激振动的抑振效果已经十分明显，振幅比从0.98 下降到0.008，振幅比降低99.2%；当旋转翼旋转角速度继续增加后，会导致输入能量的增加，造成该主动控制方法成本的增加，因此可以认为ω=3.0 rad/s（T7）为最优的控制效果参数。

4.2 约化速度对立管结构涡激振动抑振的影响

由图6可知，随着约化速度（雷诺数）的增加，海洋立管本身的振幅会发生先增加后减小的变化趋势，因此必须考虑约化速度对立管涡激振动控制效果的影响。同时，根据上节可知，T7（ω=3.0 rad/s）的控制效果最优，此节对比T1 和T7 立管的涡激振动响应随约化速度的变化。图8 所示为T1 和T7 的振幅比随约化速度增加而发生变化的趋势。由图8可知：随着约化速度的增加，旋转翼始终具有较好的控制效果，振幅比降低明显，振幅比控制在0.01以内。

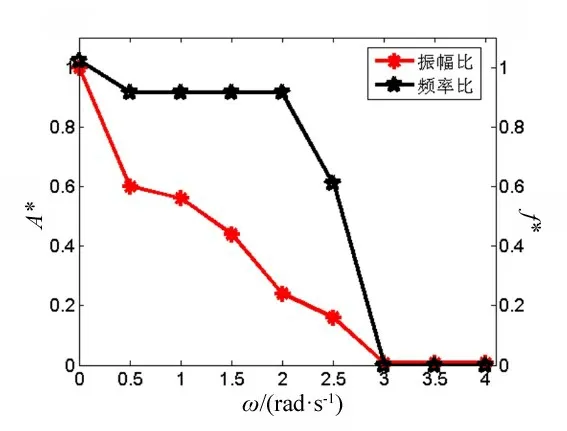
图7 海洋立管涡激振动响应与旋转翼旋转角速度的关系（Ur=4.5）Fig.7 The relationship between VIV responses of marine riser and rotating velocity of rotating wings

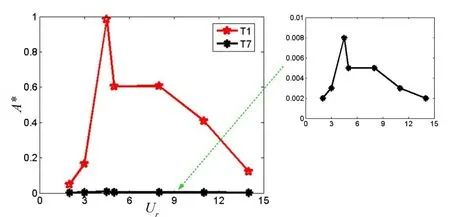
图8 海洋立管涡激振动响应与约化速度的关系Fig.8 The relationship between VIV responses of marine riser and reduced velocity

4.3 尾流场分析

图9所示为海洋立管T1的振幅比、升力变化曲线以及涡量云图变化（Ur=4.5）。以T1、T3、T6和T7为例进行分析,图10所示为振幅比曲线对比，图11所示为涡量云图对比（Ur=4.5）。

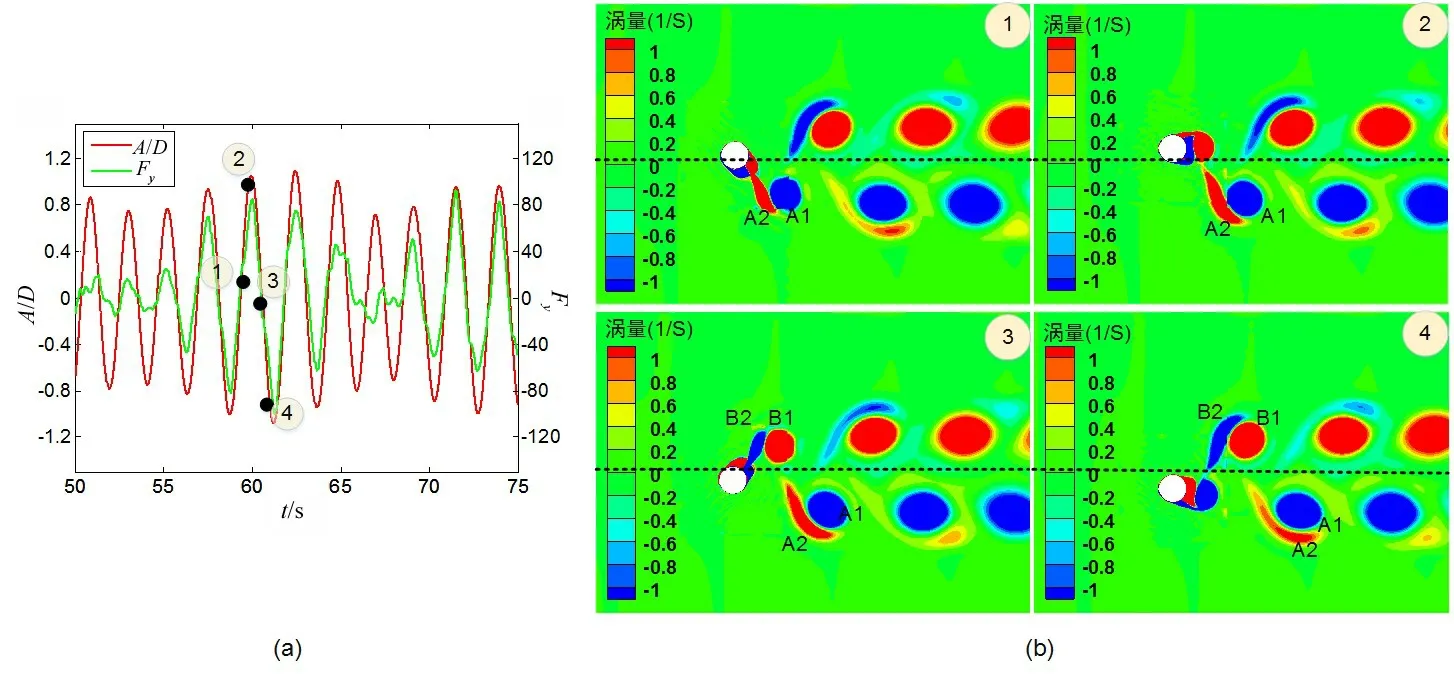
图9 T1的振幅比、升力变化曲线以及涡量云图变化（Ur=4.5）Fig.9 Amplitude ratio,lift curve and vortex nephograms of T1(Ur=4.5)

由图9 可知，海洋立管涡激振动响应的振幅比变化与升力变化是同步的，升力驱动立管结构运动；当海流作用于海洋立管时，结构后方会有周期性脱落的漩涡产生，周期性脱落的漩涡会造成作用在结构上流体力发生周期性波动，周期性的脉动升力驱动立管结构周期性运动。

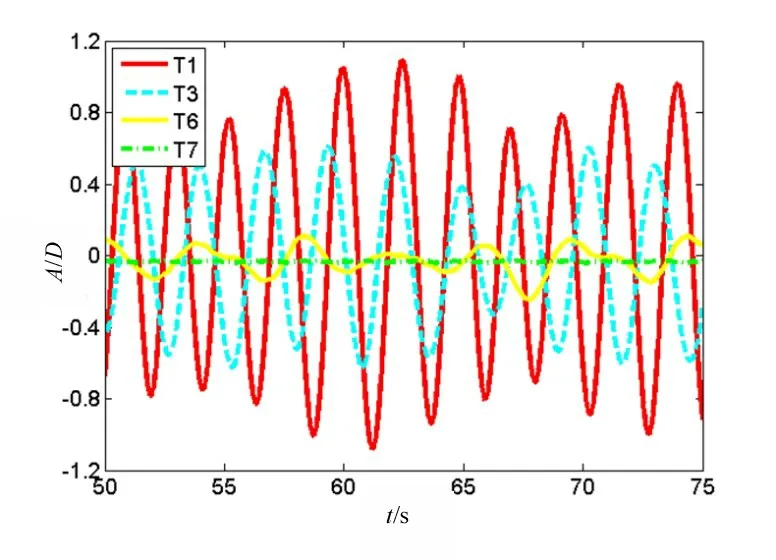
图10 T1、T3、T6和T7的振幅比曲线对比（Ur=4.5）Fig.10 Comparison of amplitude ratios curves of T1,T3,T6 and T7(Ur=4.5)

由图10可知，旋转翼的旋转运动会造成海洋立管涡激振动响应振幅比的降低；当ω=3.0 rad/s（T7）时，振幅的周期性波动几乎趋于0，振动得到明显的抑制，振幅比降低99.2%。

图11 T1、T3、T6和T7的涡量云图对比（Ur=4.5）Fig.11 Comparison of vortex nephograms of T1,T3,T6 and T7(Ur=4.5)

由图11 可知，旋转翼的旋转运动会破坏海洋立管脱落的尾流漩涡，从而破坏海洋立管的周期性振动；当ω=3.0 rad/s（T7）时，尾流漩涡基本不再发生周期性脱落，涡激振动得到有效控制。

5 结 论

本文通过非定常流体数值计算方法求解分析了旋转翼对海洋立管涡激振动的抑振作用，研究发现：

（1）随着旋转翼旋转角速度的增加，立管的振幅比逐渐减小，最后基本不变，处于较低的振幅比状态；当ω=3.0 rad/s 时，振幅比为0.008（Ur=4.5），抑制振动效果十分明显；随着旋转翼旋转角速度的增加，立管涡脱落的频率比先减小，后趋于不变；当旋转角速度大于2.0 rad/s时，频率比开始迅速下降；当ω=3.0 rad/s时，频率比接近于0，抑制涡脱落的效果十分显著；

（2）当ω=3.0 rad/s 时，海洋立管涡激振动的抑振效果已经十分明显，振幅比从0.98 下降到0.008，振幅比降低99.2%；当旋转翼旋转角速度继续增加后，会导致输入能量的增加，造成该主动控制方法成本的增加，因此可以认为ω=3.0 rad/s（T7）为最优的控制效果参数；

（3）随着约化速度的增加，旋转翼始终具有较好的控制效果（ω=3.0 rad/s），振幅比降低明显，振幅比控制在0.01以内；

（4）海洋立管涡激振动响应的振幅比变化与升力变化是同步的，升力驱动立管结构运动；当海流作用于海洋立管时，结构后方会有周期性脱落的漩涡产生，周期性脱落的漩涡会造成作用在结构上流体力发生周期性波动，周期性的脉动升力驱动立管结构周期性运动。旋转翼的旋转运动会破坏海洋立管脱落的尾流漩涡，从而破坏海洋立管的周期性振动；当ω=3.0 rad/s（T7）时，尾流漩涡基本不再发生周期性脱落，涡激振动得到有效控制。