突破立体几何中的探索性问题

◇ 新疆 傅祖勇

探索性试题能够培养学生发现问题、解决问题的能力,对学生空间想象和数学能力的提升也起着不可或缺的作用．探索性问题是相对于封闭问题而言的,立体几何探索性问题的条件或结论不完备,需要学生自己去思考、挖掘．

1 空间平行关系的探索性问题

例1如图1所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC＝PD＝2,E为PC的中点,CB＝3CG．

(1)求证：PC⊥BC；

(2)AD边上是否存在一点M,使得PA∥平面MEG?若存在,求出AM的长；若不存在,请说明理由．

图1

解析

(1)证明：因为PD⊥平面ABCD,BC⊂平面ABCD,所以PD⊥BC．因为四边形ABCD是正方形,所以BC⊥CD．

又PD∩CD＝D,PD⊂平面PCD,CD⊂平面PCD,所以BC⊥平面PCD．因为PC⊂平面PCD,所以PC⊥BC．

(2)如图2所示,连接AC,BD交于点O,连接EO,GO,延长GO交AD于点M,连接EM,则PA∥平面MEG．因为E为PC的中点,O是AC的中点,所以EO∥PA．

图2

因为EO⊂平面MEG,PA⊄平面MEG,所以PA∥平面MEG．因为△OCG≌△OAM,所以AM＝,所以AM的长为

点评

对于空间平行关系的探索性问题,需要对命题条件和命题结论有个深刻的认知,只有知道条件和结论分别是什么,才能更好地完成猜想与证明过程．解题时要能够灵活将代数问题与几何问题进行相互转化．

2 空间垂直关系的探索性问题

例2如图3,已知三棱柱ABC-A′B′C′的侧棱垂直于底面,AB＝AC,∠BAC＝90°,点M,N分别为A′B和B′C′的中点．

(1)求证：MN∥平面AA′C′C；

(2)若AB＝λ AA′,当λ取何值时,CN⊥平面A′MN,请尝试证明你的结论．

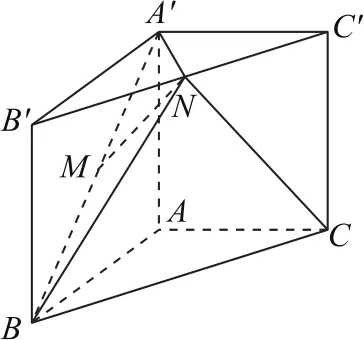
图3

解析

(1)证明：如图4,取A′B′的中点E,连接ME,NE．

因为M,N分别为A′B和B′C′的中点,所以NE∥A′C′,ME∥AA′．又因为A′C′⊂平面AA′C′C,A′A⊂平面AA′C′C,所以ME∥ 平面AA′C′C,NE∥平面AA′C′C,所以平面MNE∥平面AA′C′C,因为MN⊂平面MNE,所以MN∥平面AA′C′C．

(2)连接BN,设AA′＝a,则AB＝λ AA′＝λ a,由题意可知,,因为三棱柱ABC-A′B′C′的侧棱垂直于底面,故平面A′B′C′⊥平面BB′C′C,因为AB＝AC,点N是B′C′的中点,所以A′B′＝A′C′,A′N⊥B′C′,所以A′N⊥平面BB′C′C,所以CN⊥A′N,要使CN⊥平面A′MN,只需CN⊥BN即可,所以CN2＋BN2＝BC2,即,解得,故当时,CN⊥平面A′MN．

图4

点评

这类问题的结论已经给定,探求此结论成立的条件,常规的解决方法是执果索因、逆向求索或合理猜想,最后加以证明,即多采用分析或猜想证明．

3 空间距离的探索性问题

例3如图5所示,已知AB⊥平面BCE,CD∥AB,△BCE是等腰直角三角形,其中,且AB＝BC＝2CD＝2．

(1)在线段BE上是否存在一点F,使CF∥平面ADE?

(2)求线段AB上是否存在点M,使点B到平面CEM的距离等于1?如存在,试判断点M的个数；如不存在,请说明理由．

图5

解析

(1)当F为BE的中点时,CF∥平面ADE．取BE的中点F,AE的中点G,连接FG,GD,CF,所以AB．因为,所以CDGF,所以CDGF是平行四边形,所以CF∥平面ADE．

(2)如图6所示,设MB＝x,2＝2,又因为MB⊥平面BEC,所以,则在Rt△MBE中,

图6

取EC的中点H,因为ME＝MC,所以MH⊥EC,而

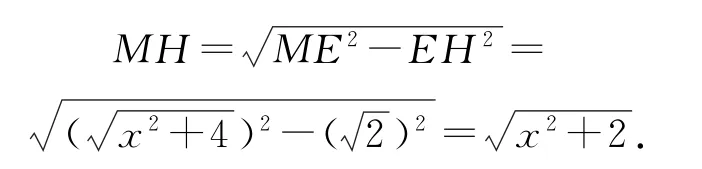
故

因为点B到平面CEM的距离等于1,所以

而VB-MEC＝VM-BEC,所以,解得因此,在线段AB上只存在一点M,当且仅当BM＝时,点B到平面C EM的距离等于1．

点评

求点到平面的距离的探索性问题主要有直接法(直接由点作垂线,求垂线段的长)、转移法(转化成求另一点到该平面的距离)、等体积法等．另外,解答该题时容易忽视点P在线段AB上的限制条件,误以为方程的解就是结果而忽视λ的取值范围导致出现错误．