面向“智慧政务”文本挖掘的研究＊

张 影，刘红美

（三峡大学理学院，湖北 宜昌 443000）

在大数据和信息化的时代特征下，网络平台无疑为收集海量的文本数据提供了便捷，如何快速、有效、精确地筛选出主要信息并对其分类、答复，是一个需要不断精化、持续进步的课题。为了不断改进智能文本挖掘模型及算法，对计算机读取的研究引起了人们的广泛关注。

计算机读取技术的发展对信息检索、自动文摘、答复系统等自然语言处理研究任务有积极作用，同时也能够直接改善搜索引擎、智能APP 等产品的用户体验。因此，以读取筛选、文本挖掘为契机研究机器自然语言的技术，在有限的信息范围内要做到准确全面处理，具有重要的研究与应用价值。

网络问政平台作为一种新兴模式，以其快捷、不受时空限制等优点而受到政府机构的青睐。借助网政平台收集群众反馈的海量信息数据，是实时了解民意、汇聚民智、凝聚民气的重要渠道。如果能从群众留下的信息中敏锐地捕捉信号，不仅能够提升政府的管理水平，同时也能更好地为群众百姓提供服务，进行互赢模式间的双向信息传递。本文针对智慧政务的文本挖掘问题，采用潜在语义分析、聚类分析、主成分分析方法，基于留言的一级标签分类，实现了对热点问题的挖掘和排名。

1 预处理工作

数据来源为“智慧政务”互联网公开渠道，对其留言的一级标签分类简述的处理过程如下。

基于Python，采用sklearn 提供的函数划分数据集，实现分层抽样，以保证60%训练集、20%验证集、20%测试集3 部分数据的一级标签分布均匀性。

数据清洗：清除附件“留言详情”栏附有HTML 标签、URL 地址等文本标记的无效分类信息以及标点符号，去除噪声，为后续分类奠定基础。分词采用Python 开发的一个中文分词模块——jieba 分词器，分词效果如图1 所示。

建立停用词字典：维护一个停用词表，在分词后将停用词去除。

基于TF-IDF 对文本特征进行提取[1]，以向量空间模型（VSM）[2]表示文本留言。

Word2vec 是一个Estimator，它采用一系列代表文档的词语来训练Word2vec model。该模型将每个词语映射到一个固定大小的词向量，将文本结构化。

2 模型的建立

2.1 热点问题的挖掘

2.1.1 语义空间降维

通常情况下，当得出文本向量后，直接比较两向量的夹角的余弦值，并进行相似度计算。但是，针对智慧政务平台上的留言所构造的词汇-文本矩阵是一个巨大矩阵，计算起来比较困难。另外，留言文本信息中存在同义词和近义词等词语，即使通过特征抽取转化得到的文本向量，可能仍然达不到自然语言属性本质的要求。

因此，这里需要借用潜在语义分析（Latent Semantic Semantic Analysis，LSA）理论[3]将留言信息中文本向量空间中非完全正交的多维特征投影到维数较少的潜在语义空间上。而LSA 对特征空间进行处理时用的关键技术是奇异值分解（Singular Value Decomposition，SVD），在统计学上，它是针对矩阵中的特征向量进行分解和压缩的技术。

图1 过滤后分词结果

2.1.1.1 一般的奇异值分解

奇异值分解可以将网页文本通过向量转换后的非完全正交的多维特征投影到较小的一个潜在语义空间中，同时保持原空间的语义特征，从而可以实现对特征空间的降噪和降维处理。奇异值分解是一类矩阵分解，是正规矩阵酉对角化的一种推广。对于任意的矩阵A，其奇异值分解表达式为A=U∑VT，其中A∈Rm×n，且Rank（A）≤min（m，n），正交矩阵（即A的左右奇异向量），U∈Rm×m和V∈Rn×n，半正定对角矩阵…≥σr≥0，UUT=Im，VVT=In。

在奇异值分解A=U∑VT中，有A的k阶截距阵即：

由上述可知，在F-范数中，Ak是和A相似度最高的k秩矩阵，这将用于矩阵降维。

2.1.1.2 词汇-文本矩阵的奇异值分解

对于矩阵词汇-文档矩阵Am×n的奇异值分解可表示为：

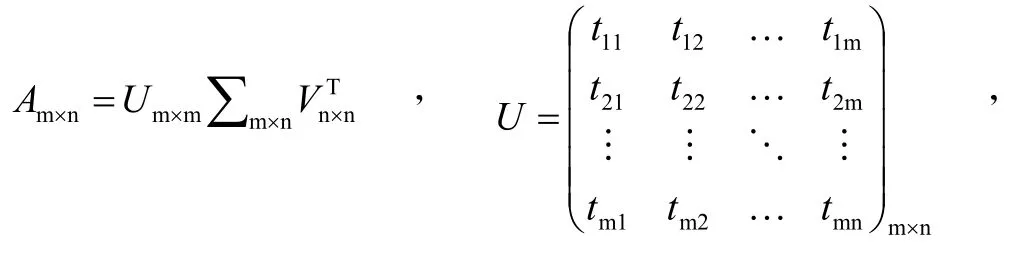
∑矩阵表示某类词与留言文本之间的相关性。在生成的“语义空间”中，大的奇异值对应的维度更具有词的共性，而小的奇异值所对应的维度更具有词的个性。

在A矩阵中，Ui和∑决定每一行i的信息，和∑决定每一列j的信息。对角矩阵∑的信息主要由奇异值大小决定，奇异值越大，对∑的影响也越大，对整个矩阵的影响也越大。因此，可以通过保留较大的奇异值，删去较小的奇异值，从而对矩阵进行行与列的降维处理。

另一方面，∑矩阵的奇异值σ1≥σ2≥…≥σr中，如果σi（1，2，…，r）的值比较小，则它对整个词汇-文本矩阵A的影响也小，所以可以删除对矩阵A影响较小的σ以及对应的U和VT的信息，保留影响较大主要信息，得到Am×n的近似矩阵Ak。

在不影响留言文本分析结果的同时对矩阵进行降维处理，简化了运算的复杂度。

通常情况下，前10%的奇异值的和占总奇异值和的99%。k值的选取决定着近似矩阵的相似性，k值的大小与主要信息的承载量成正比，k值越大，所包含的主要信息越多，相应地对次要信息的删除就会减少，且会减弱降维的效果，而取值越小，则会删除更多信息，以至于剩下的信息没有很好的区分度。

由于在∑矩阵中只取非零的奇异值，只要满足m×n≥m×k+n×k+k×k（近似矩阵中的三个矩阵的元素个数），即可以去掉次要的信息，保留主要信息，达到降维的目的，降低计算机对存储的要求，从而保证聚类的准确性。

2.1.2 向量语义化

对某一特征项为n的文本向量t进行奇异值分解以及t在进行k维映射后得到的向量t´为：进行语义压缩后的向量被认为投影在同一空间里，然后方可进行文本聚类。

2.1.3 文本聚类

2.1.3.1 留言文本相似度计算

为表示不同留言间的差异，先计算基于距离度量的欧几里得距离，再转化为余弦相似度[4]。

令i=（x1，x2，…，xp）和j=（y1，y2，…，yp）是两个被p个数值属性标记的对象，则对象i和j之间的欧氏距离，以及根据余弦相似度和欧氏距离的关系，留言文本间的余弦相似度可表示为：

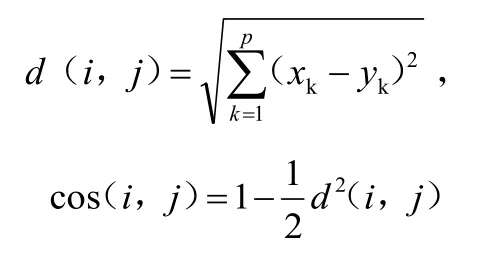
2.1.3.2 基于K-means 聚类[5]的文本聚类

该算法要求在计算之前给定k值。本文通过初步估计留言数据中的热点问题数，并以此给定k的值，这里令k=7 为初值，根据后续的热度值大小，进行适当增减k的值，也就是对热点问题的数量进行调控。原理流程如图2 所示。主成分基本步骤如图3 所示。

图2 K-means 聚类流程图

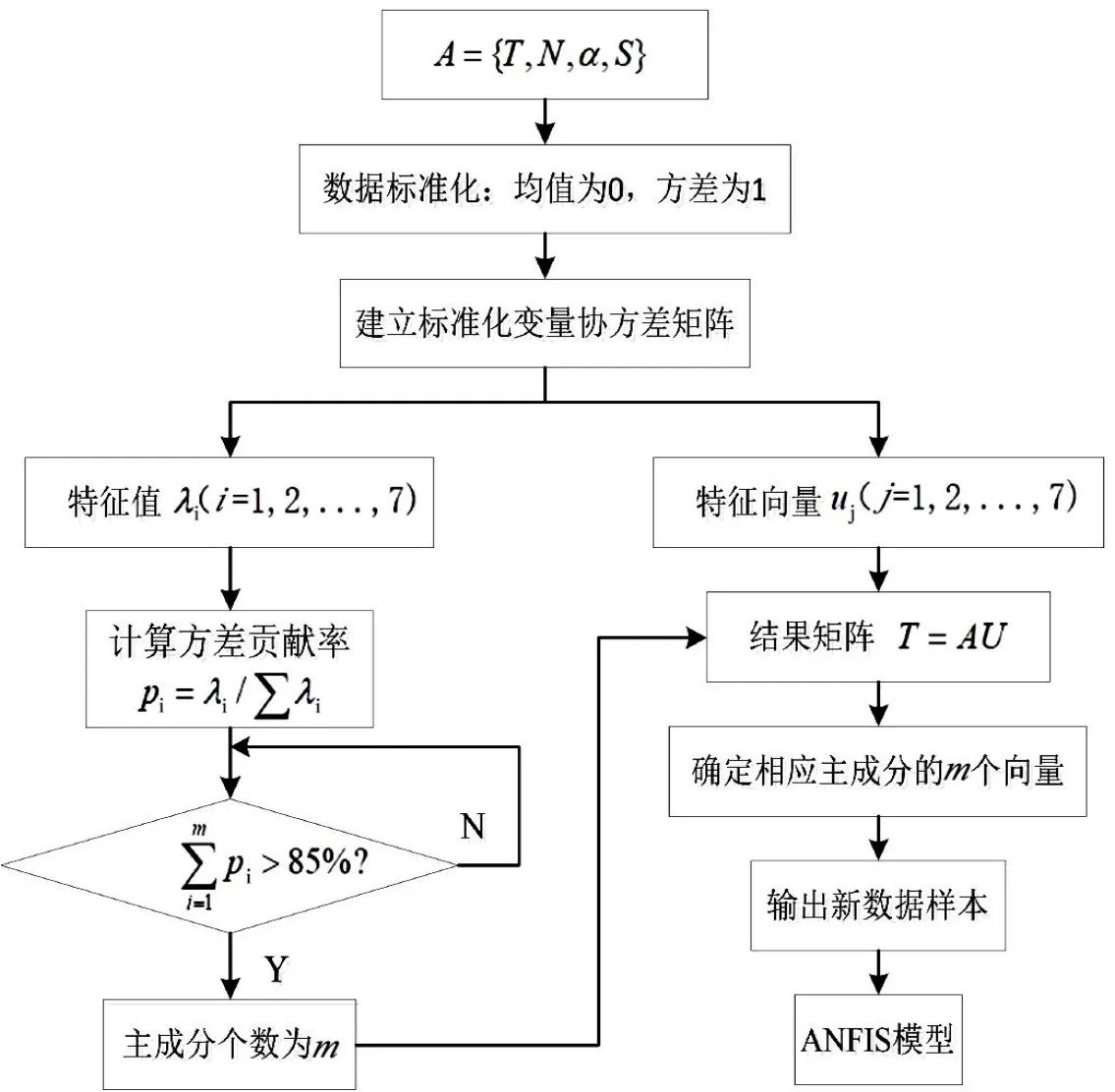
图3 主成分基本步骤

2.2 热点问题的排名

2.2.1 矩阵和特征量的计算

考虑到影响热点问题间的差异性，将每个热点问题所包含的留言数、留言时间密集度、点赞数、反对数等作为评价指标。

希望用较少的综合变量来代替原来较多的变量，而这几个综合变量又能尽可能多地反映原来变量的信息，并且彼此之间互不相关。

标准化指标变量：选取m1个指标，

计算相关系数矩阵R的特征值λ1≥λ2≥…≥λm1≥0，及对应的特征向量a1，a2，…，am1，其中aj=[a1j，a2j，…，am1j]T，由特征向量组成m1个新的指标变量：

2.2.2 主成分的选择

为达到降维，选取部分更具代表性的主成分，计算各主成分Fj的信息贡献率bj及F1，F2，…，Fp的累计贡献率αp：

当αp接近于1（取αp＞0.95）时，则选择前p个指标变量F1，F2，…，Fp作为p个主成分，代替原来m1个指标变量，从而可对p个主成分进行综合分析。

2.2.3 主成分分析的综合评价

筛选出p个主成分；通过标准化指标前特征向量数值的相对大小，分析各主成分主要反映的对应指标。

以p个主成分的信息贡献率为权重，构建综合评价模型求出综合分

3 实证分析求解

在纯文字文本下，调用Python 的库函数，根据语义分析LSA 的奇异值分解SVD 技术和K-means 算法，实现留言语义空间降维，将相似问题聚类并实现热点挖掘。

经统计，数据来源共有4 326 条留言，经Python 处理得每个热点的留言信息，首先分层筛选出留言文本在前175 条的热点占总留言内容的98.86%，因此其余留言可以忽略不计，进而构造上述指标，利用SPSS 对其进行综合排名。

对筛选得到的数据导入SPSS 进行标准化处理，得到各标准化指标的解释方差，如表1 所示。

由表1 可知，成分1～6 的因子比较重要，其方差累计贡献率达到了92.6%（＞90%）符合主成分分析方差提取原则。考虑到因子较多时，剔除主成分的第一行特征值小于1的因子，因此成分1～4 的因子是主导作用的。

表1 解释方差

对筛选出的4 个主成分，经计算得如下各标准化指标前的特征向量表，如表2 所示。

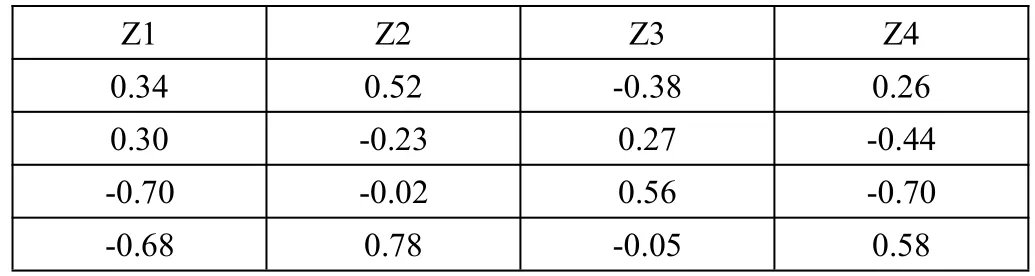
表2 特征向量矩阵

将得到的特征向量与标准化后的数据相乘，可以得出各个主成分得分值。以每个主成分所对应的特征值占总特征值的比例作为权重计算主成分综合得分F，其中λi表示第i主成分因子的特征值。

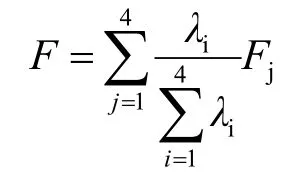
得到综合排名分F以及排名前5 的热点问题，如表3所示。

表3 热点问题表

4 结语

本文的研究是针对智慧政务平台的留言信息，结合所建模型以及算法对留言进行了充分挖掘，原理可解释性极强，实验也表明其结果具有可靠性和有效性，非常适用于此类大量文本数据的情况。对热点问题的排名采用主成分分析法，很好消除了评价指标之间的相关影响，减少了指标选择的工作量，且便于实现。

为了更好地对类似政务平台单位进行政务文本挖掘，解决文本热点留言的挖掘问题，推进简化平台的发展，对智慧政务留言信息文本进行了详细分析研究，具有一定的理论研究意义和广泛的实际应用价值。

对留言文本采用降维方式匹配筛选的综合模型，如何精简所建模型及算法，同时对留言的情感语义进行分析，是笔者们下一步的工作。