图片模糊聚合算子及其在多属性决策中的应用
2021-01-28龙慧丰罗敏霞
龙慧丰,罗敏霞
(中国计量大学 理学院,浙江 杭州 310018)
直觉模糊集是模糊集的一般化,由隶属度和非隶属度表示,且隶属度与非隶属度之和不超过1,直觉模糊集与区间值模糊集是等价的。许多学者对直觉模糊集及区间值模糊集做了大量研究。文献[1]研究了基于左连续区间值t-可表示三角范数的模糊推理五蕴涵算法。文献[2-8]研究了多属性决策的方法。然而,直觉模糊集不能表示具有非一致性的信息。投票就是一个很好的例子:投票结果按选民人数分为四组,分别是赞成、反对、弃权和拒绝投票。为了处理这一类型的问题,文献[9]提出了图片模糊集,作为直觉模糊集的直接扩展,以正隶属度、中立隶属度和负隶属度表示,且这些隶属度之和不超过1。一些基于图片模糊集的多属性决策的方法已经被许多学者提出[10-14]。
在多属性决策过程中,聚合算子是重要的工具。文献[11]提出了图片模糊算术聚合算子。文献[15]提出了一些图片模糊聚合算子,并将其应用于多属性决策。文献[16]从概率的角度提出了一些图片模糊几何聚合算子,并将其应用于多属性决策。文献[17]提出了基于度量、Shapley模糊度量和幂聚合算子的加权几何聚合算子。
显然,上述聚合算子是基于一般三角范数及其对偶的三角余范的代数运算法则。在多属性决策过程中,上述聚合算子不能为决策者提供更多的选择。因此,学者们基于三角范数簇及其对偶的三角余范簇提出了一些聚合算子。文献[18]提出了图片模糊爱因斯坦聚合算子;文献[12]提出了图片模糊Hamacher聚合算子;文献[19]提出了图片模糊Dombi聚合算子,并应用到多属性决策问题。但是,文献[12]的图片模糊Hamacher聚合算子的计算过程比较复杂。文献[19]的图片模糊Dombi聚合算子聚合的结果不稳定,因为取不同的参数时,得到了不同的结果(见例3.1的表5)。
此外,目前基于图片模糊集的聚合算子没有公理化定义,现有的聚合算子没有严格的逻辑基础[11,12,18,19],例如:α⊗β=
1 预备知识
定义1.1[9]在论域X上的图片模糊集A形式如下:A={
则(D*,≤D*)是一个完备格。D*上的最大元和最小元分别是1D*=<1,0,0>和0D*=<0,0,1>。
定义1.2[21]Frank三角范数簇TF:[0,1]2→[0,1],及Frank三角余范簇SF:[0,1]2→[0,1]如下:对于所有的x,y∈[0,1],
定义1.3[20]一个图片模糊三角范数T称为可表示的,如果存在两个三角范数T1,T2和一个三角余范S3在[0,1],对于所有的x=
x=
S(A,B)=
定义1.4[11,22]令α=<μα,ηα,να>是一个图片模糊数,图片模糊数的分数函数和精确函数定义为:
g(α)=μα-να,g(α)∈[-1,1],
h(α)=μα+ηα+να,h(α)∈[0,1]。
定义1.5[11]令α=<μα,ηα,να>和β=<μβ,ηβ,νβ>∈D*,如果g(α)>g(β),则α>β;如果g(α)=g(β),则
1)h(α)>h(β),则α>β;
2)h(α)=h(β),则α=β。

图片模糊加权平均(PFWA)聚合算子和图片模糊加权几何(PFWG)聚合算子[11]:


(2)
图片模糊Hamacher加权平均(PFHWA)聚合算子和图片模糊Hamacher加权几何(PFHWG)算子[12]:

(3)
(4)
图片模糊Dombi加权平均(PFDWA)聚合算子和图片模糊Dombi加权几何(PFDWG)聚合算子[19]:
PFDWA(α1,α2,…,αn)=

PFDWG(α1,α2,…,αn)=

2 新的图片模糊聚合算子
定义2.1A称为D*上一个聚合算子,如果A满足如下条件:(P1)A(α)=α(∀α∈D*);(P2)令αj,βj∈D*如果αj≤βj(j=1,2,…,n),则A(α1,α2,…,αn)≤A(β1,β2,…,βn);
定义2.2令α=<μα,ηα,να>和β=<μβ,ηβ,νβ>是两个图片模糊数,T是Frank三角范数,S是对偶的Frank三角余范,并且λ∈[0,+∞),则Frank乘法、Frank加法、Frank数乘和Frank幂运算定义如下:
α⊗Fβ=
α⊕Fβ=
kα=
ak=

2.1 图片模糊Frank加权平均聚合算子
定理2.1令
αj=<μαj,ηαj,ναj>∈D*(j=1,2,…,n),λ∈[0,+∞),映射PFFWA:(D*)n→D*定义如下:

(7)

证明:(P1)如果α=<μ,η,ν>,ω=1,则有
PFFWA(<μ,η,ν>)=<1-logλ(1+(λ1-μ-1)ω),
logλ(1+(λη-1)ω),logλ(1+(λν-1)ω)>=<1-
logλ(1+(λ1-μ-1)),logλ(1+(λη-1)),logλ(1+(λν-1))>=<1-logλ(λ1-μ),logλ(λη),logλ(λν)>=<1-(1-μ),η,ν>=<μ,η,ν>。
(P2)令
αj=<μαj,ηαj,ναj>,βj=<μβj,ηβj,νβj>∈D*,αj≤D*βj⟺(μαj<μβj,ναj≥νβj)
∨(μαj=μβj,ναj>νβj)
∨(μαj=μβj,ναj=νβj,ηαj≤ηβj)。
1)如果αj≤D*βj(μαj<μβj,ναj≥νβj),则:

因此,我们可以得到
PFFWA(α1,α2,…,αn)≤
PFFWA(β1,β2,…,βn)。
2)如果αj≤D*βj(μαj=μβj,ναj>νβj),则:

因此,我们可以得到
PFFWA(α1,α2,…,αn)≤
PFFWA(β1,β2,…,βn)。
3)如果
αj≤D*βj(μαj=μβj,ναj=νβj,ηαj≤ηβj),
则:

因此,我们可以得到
PFFWA(α1,α2,…,αn)≤
PFFWA(β1,β2,…,βn)。
综上所述,我们可以得到,如果αj≤D*βj,则:
PFFWA(α1,α2,…,αn)≤
PFFWA(β1,β2,…,βn)。
(P3) 如果αj=0D*(j=1,2,…,n),则:

(λ1-0)ω1(λ1-0)ω2…(λ1-0)ωn),logλ(1+(λ0-1)ω1
(λ0-1)ω2…(λ0-1)ωn),logλ(1+(λ1-1)ω1
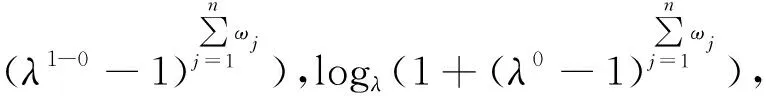
(λ1-0-1)),logλ(1+(λ0-1)),logλ(1+
(λ1-1))>=<1-logλλ,logλ1,logλλ>
=<0,0,1>=0D*。
(P4) 如果αj=1D*(j=1,2,…,n),则:
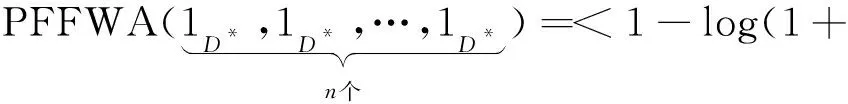
(λ1-1-1)ω1(λ1-1-1)ω2…(λ1-1-1)ωn),logλ(1+
(λ0-1)ω1(λ0-1)ω2…(λ0-1)ωn),logλ(1+

因此,PFFWA是一个聚合算子。
2.2 图片模糊Frank加权几何聚合算子
定理2.2令
αj=<μαj,ηαj,ναj>∈D*(j=1,2,…,n),一个映射PFFWG:(D*)n→D*定义如下:

(8)
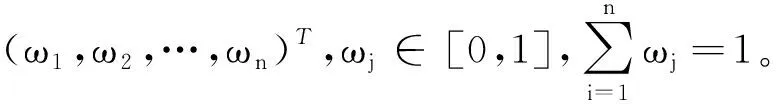
3 算法与应用
3.1 算 法

第一步:使用PFFWA或PFFWG聚合算子,计算每个方案Ai(i=1,2,…,m)聚合的值。
第二步:使用定义1.4,计算聚合值的分数函数值g(Ai)。
第三步:使用定义1.5,按照递减顺序对可选方案进行排序,分数函数最大的方案则是最好的方案。
本文以上算法具有三个特色。1)此算法有严格的逻辑基础,满足聚合算子的公理化定义。2)利用此算法聚合保证了聚合的结果是图片模糊数,克服了存在的算法的缺陷,例如:α⊗β=
3.2 应 用
3.2.1 应用到多属性决策
例3.1[19]为了确定最有利的技术商业化,有一个委员会选择了5个可行的新兴技术企业Ai(i=1,2,3,4,5),他们选择了四个属性对5个可能的新兴技术企业进行了评估,分别为C1:技术进步;C2:潜在市场和市场风险;C3:工业化框架,人力资源和融投资;C4:就业的形成和科学技术的进步。属性的加权向量ω=(0.2,0.1,0.3,0.4)T,决策矩阵以图片模糊数的形式给出,见表1。

表1 决策矩阵
第一步:取λ=2,使用PFFWA和PFFWG分别去计算可选方案聚合的值,聚合结果见表2。

表2 新兴技术企业的聚合值
第二步:使用定义1.4,计算聚合值的分数函数,计算结果见表3。

表3 分数函数的值
第三步:将新兴技术企业按照分数函数值降序排列,分数函数值最大的方案为最佳方案,排序结果见表4。

表4 新兴技术企业的排序
由表4可知,使用PFFWA和PFFWG聚合算子计算的结果是一致的,最好的方案是A3。
3.2.2 与一些聚合算子的比较
通过与一些聚合算子的对比:文献[11]的图片模糊加权平均(PFWA)聚合算子和图片模糊加权几何(PFWG)聚合算子;文献[12]的图片模糊Hamacher加权平均(PFHWA)聚合算子和图片模糊Hamacher加权几何(PFHWG)聚合算子;文献[19]的图片模糊Dombi加权平均(PFDWA)聚合算子和图片模糊Dombi加权几何(PFDWG)聚合算子。结果的比较见表5。

表5 与一些聚合算子的比较结果
从表5可看出,利用本文提出的聚合算子聚合的结果与大部分聚合算子聚合的结果是相同的,最好的方案都是A3。但是,文献[11]的聚合算子不具有灵活性,因为它不含参数。虽然文献[12]和文献[19]的聚合算子都含有参数,但是文献[12]的图片模糊Hamacher聚合算子的计算过程比较复杂。文献[19]的Dombi聚合算子的聚合结果不稳定。因此,本文提出的图片模糊Frank聚合算子更灵活、更有效、更实用。
4 结 论
在本文中,我们给出了图片模糊聚合算子的公理化定义,为聚合算子研究提供了理论基础。基于图片模糊可表示三角范数和Frank三角范数,提出了一些图片模糊运算,克服一些已有运算的缺陷。在此基础上,我们提出图片模糊Frank加权平均(PFFWA)聚合算子和图片模糊Frank加权几何(PFFWG)聚合算子,并证明它们满足公理化定义。此外,我们将所提出的聚合算子应用于多属性决策问题。实例结果表明,与一些聚合算子相比,新的聚合算子比一些聚合算子更可靠、更灵活。进一步研究中,我们考虑将PFFWA和PFFWG聚合算子应用到模式识别、医疗诊断和风险分析等领域。
