线性六边形链图的半全控制数

2021-01-28宋曦,陈琴

中国计量大学学报 2020年4期

宋曦,陈琴

(中国计量大学理学院,浙江杭州 310018)

图的控制理论主要研究图的各种控制参数的值。1962年Oystein正式提出“控制数”的概念并于1965年发表成果[1],之后有关图的控制数问题得到了迅速发展。控制集和控制数的重要性不仅仅体现在理论上,而且在生活中的应用也十分广泛。在许多选址问题上都需要借鉴控制数问题,比如在某个城市的小区之间建立快递物流服务站,最少需要建立多少个服务站才能保证物流运输的畅通。而在实际生活的各种要求限制下,又延伸出许多不同类别的控制数问题,如全控制数[2]、罗马控制数[3]等。赵敏和陈琴[4]将图的控制理论与电力网相结合,研究了几类电力控制数为1的平方图。Goddard等[5]在2014年提出并研究了图的半全控制集,此后许多学者对该问题进行了研究,并取得丰硕的成果。朱恩强等研究了无爪三正则图[6]、线图[7]的半全控制数。2019年,Henning等[8]证明了平面图、分裂图、弦二部图的半全控制数对应的判定问题是NP-完备的。陈琴等[9]研究了图的半全控制数的剖分数。

1 准备工作设

G=(V,E)是一个无向简单图,其中V是G的顶点集,E是G的边集。对于集合D⊆V,若VD中每个顶点都至少与D中一个顶点相邻,则称D是G的一个控制集。G的控制数是G的最小控制集的顶点个数,用γ(G)表示。对于集合S⊆V,若S是G的控制集,且对于S中的每个顶点,在S中都存在另一个顶点与其距离小于等于2,则称S是G的半全控制集。G的最小半全控制集的顶点个数称为G的半全控制数,记为γt2(G)。对任意的v∈V,v的开邻域记为N(v)={u∈V|uv∈E},闭邻域记为N[v]={v}∪N(v)。用Cn=x1x2…xnx1表示n个顶点的圈。用Hm表示由m个六边形组成的线性六边形链,图1为H3。由于互为同构图的半全控制数相同,因此每个六边形可以用图2中的同构图圈C6来代替。为了方便研究,令Hm的顶点集为{xi,j|1≤i≤n,j=1,2},其中n=2m+1,如图3。对任意的i=1,2…,n,令Yi={xi,j|j=1,2}。

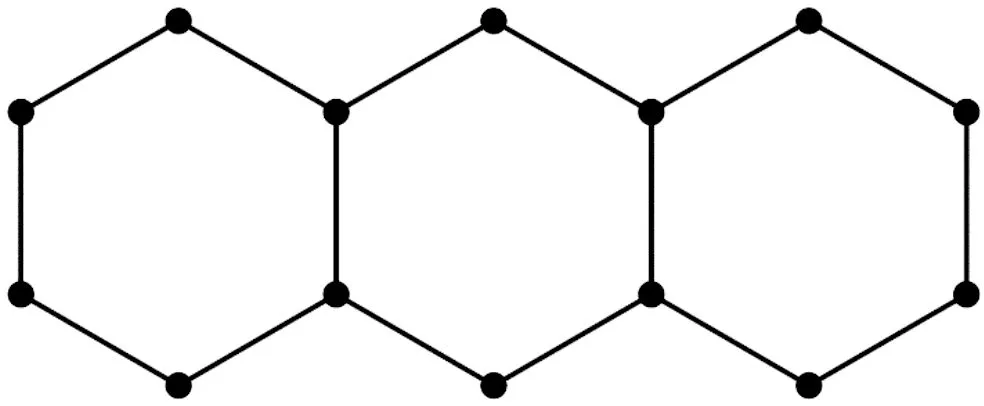
图1 图H3Figure 1 Graph H3

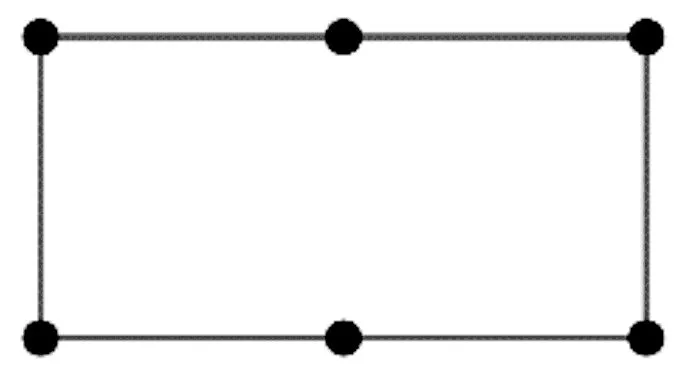
图2 六边形的同构图圈C6Figure 2 Isomorphic graph C6 of hexagon

图3 HmFigure 3 Hm

2 主要结果及其证明

引理2.1设D是Hm+3的一个最小半全控制集,令n=2m+1,Sn,2为Hm+3中由顶点{xij|1≤i≤n,j=1,2}导出的子图,即Sn,2与Hm同构,如图4,则在Hm+3中,有|D∩(Yn+1∪Yn+2∪Yn+3∪Yn+4∪Yn+5∪Yn+6)|≥4。特别地,当|D∩(Yn+1∪Yn+2∪Yn+3∪Yn+4∪Yn+5∪Yn+6)|=4时,D∩Sn,2是Sn,2的一个半全控制集。

图4 引理2.1中Sn,2与Hm+3Figure 4 Sn,2 and Hm+3 in Lemma 2.1

证明由于N[xn+5,1]∩N[xn+5,2]=∅,为了控制xn+5,1和xn+5,2,必有|D∩(Yn+6∪Yn+5∪Yn+4)|≥2。

为了控制xn+2,1,有|D∩N[xn+2,1]|≥1,即|D∩(Yn+1∪Yn+2∪Yn+3)|≥1。

情形1|D∩(Yn+6∪Yn+5∪Yn+4)|≥4

此时显然有|D∩(Yn+6∪Yn+5∪Yn+4∪Yn+3∪Yn+2∪Yn+1)|≥5,引理成立。

情形2|D∩(Yn+6∪Yn+5∪Yn+4)|=3

D∩{xn+1,1,xn+1,2,xn+2,1,xn+3,1}=∅。

因此xn,1∈D,且与xn,1距离小于等2的点在D∩Sn,2中,即D∩Sn,2是Sn,2的半全控制集,引理成立。

情形3|D∩(Yn+6∪Yn+5∪Yn+4)|=2

若|D∩Yn+4|=2,则xn+6,1和xn+6,2没有被控制;若|D∩Yn+4|=1,不妨设xn+4,1∈D,由于N[xn+6,1]∩N[xn+5,2]={xn+6,2},则xn+6,2∈D,但在D中不存在与xn+6,2距离小于等于2的点,矛盾。因此|D∩Yn+4|=0。由于

N[xn+3,1]∩N[xn+3,2]=∅,

情形3.1|D∩Yn+2|=0

此时|D∩Yn|=2。那么D∩Sn,2是Sn,2的半全控制集,引理成立。

情形3.2|D∩Yn+2|=1

由对称性,可设D∩Yn+2={xn+2,1}。此时xn,2∈D,且D中与xn,2的距离小于等于2的点在Sn,2中,即|D∩(Yn+6∪Yn+5∪Yn+4∪Yn+3∪Yn+2∪Yn+1)|=4时,D∩Sn,2是Sn,2的半全控制集,引理成立。

情形3.3|D∩Yn+2|=2

此时D∩Yn+3=∅,|D∩Yn+5|=2。但在D中不存在与xn+5,1和xn+5,2距离小于等于2的点。因此本情形不存在。

综上,引理2.1得证。

引理2.2设m≥1,则γt2(Hm)+4≤γt2(Hm+3)。

证明设D是Hm+3的一个最小半全控制集,即|D|=γt2(Hm+3)。由引理2.1知|D∩(Yn+1∪Yn+2∪Yn+3∪Yn+4∪Yn+5∪Yn+6)|≥4。

当|D∩(Yn+1∪Yn+2∪Yn+3∪Yn+4∪Yn+5∪Yn+6)|=4时,D∩Hm是Hm的一个半全控制集,此时γt2(Hm)≤γt2(Hm+3)-4。

当|D∩(Yn+1∪Yn+2∪Yn+3∪Yn+4∪Yn+5∪Yn+6)|=5时,若D∩(Yn∪Yn-1)≠∅,令D′=(D∩Hm)∪{xn,k|xn-1,3-k∈D或xn,3-k∈D,k=1,2},则D′是Hm的半全控制集,有γt2(Hm)≤|D′|≤|D|-4=γt2(Hm+3)-4,引理得证。若D∩(Yn∪Yn-1)=∅,则|D∩Yn-2|=2,令D′=(D∩Hm)∪{xn,1},易见D′是Hm的半全控制集,所以γt2(Hm)≤|D′|≤|D|-4=γt2(Hm+3)-4。

当|D∩(Yn+1∪Yn+2∪Yn+3∪Yn+4∪Yn+5∪Yn+6)|≥6时,令D′=(D∩Hm)∪{xn,1,xn,2},则D′是Hm的一个半全控制集,所以

γt2(Hm)≤|D′|≤|D|-4=γt2(Hm+3)-4。

因此,引理2.2得证。

由于H1≅C6,所以有γt2(H1)=γt2(C6)=3[1]。下面我们考虑H2和H3的半全控制数。

引理2.3γt2(H2)=4。

证明由于{x2,1,x2,2,x4,1,x4,2}是H2的一个半全控制集,所以γt2(H2)≤4。接下来证明γt2(H2)≥4。

反证法,假设D是H2的一个半全控制集且|D|≤3。由于N[x2,1]、N[x2,2]、N[x4,1]和N[x4,2]这四个闭邻域均含有D中的点,则|D∩(N[x2,1]∪N[x4,1])|=1或|D∩(N[x2,2]∪N[x4,2])|=1。不妨设|D∩(N[x2,1]∪N[x4,1])|=1,即x3,1∈D。

为了控制x1,1和x5,1,在N[x2,2]和N[x4,2]中分别有x1,2∈D、x5,2∈D。但此时在D中都没有与D中的三个点距离小于等于2的点,与D是半全控制集矛盾。从而γt2(H2)≥4。

所以γt2(H2)=4,引理2.3得证。

引理2.4γt2(H3)=6。

证明{x2,1,x2,2,x4,1,x4,2,x6,1,x6,2}是H3的一个半全控制集,所以γt2(H3)≤6。下面证明γt2(H3)≥6。

反证法,假设D是H3的一个半全控制集且|D|≤5。所以有|D∩(N[x2,1]∪N[x4,1])|=1或|D∩(N[x2,2]∪N[x4,2])|=1或|D∩(N[x4,1]∪N[x6,1])|=1或|D∩(N[x4,2]∪N[x6,2])|=1。

由对称性,不妨设|D∩(N[x2,1]∪N[x4,1])|=1,即x3,1∈D。为了控制x1,1,在N[x2,2]中有x1,2∈D,且|D∩(Y1∪Y2∪Y3)|≥3来保证D中存在与x1,2的距离小于等于2的点。由于N[x6,1]∩N[x6,2]=∅,所以|D∩(Y1∪Y2∪Y3)|=3,|D∩Y4|=0,|D∩N[x6,1]|=|D∩N[x6,2]|=1。

若x5,2∈D,为了控制x6,1、x7,1和x7,2,有x7,1∈D,但此时D中没有与x7,1距离小于等于2的点,与D是半全控制集矛盾,所以x5,2∉D。同理x5,1∉D,此时|D∩Y6|=2,但D中没有与x6,1、x6,2距离小于等于2的点,这与D是半全控制集矛盾。从而γt2(H3)≥6。

所以γt2(H3)=6,引理2.3得证。