非均匀解析函数与非均匀调和函数的刻画
2021-01-28郑允望俞荣杰陶继成
郑允望,俞荣杰,陶继成
(中国计量大学 理学院,浙江 杭州 310018)
偏微分方程理论广泛地应用于物理、生物[1]、化学等领域,特别是生物扩散模型对非均匀性研究特别重要,但是所用的底空间是均匀的,丛空间又是非均匀的,这给问题的处理带来了诸多不便[2-3]。为了解决底空间的非均匀性问题,文献[2]提出了非均匀复数域的定义,并且建立了非均匀复变函数的解析函数理论,随后又在文献[3]进一步建立了非均匀复变函数的积分理论,获得了非均匀Cauchy积分定理和非均匀Cauchy积分公式,非均匀复变函数微积分系统基本框架建立了起来。非均匀底空间的微分方程边值问题理论,积分问题等的解决是进一步把非均匀复变函数理论应用于物理、生物等领域的前提条件。调和函数在物理学中有着重要的应用,常常出现在诸如流体力学、电学、磁学等实际问题中。例如,在xy平面中,均匀薄圆盘上的温度函数H(x,y)就经常是调和函数。但是对于物体表面不等的情况,调和函数需要进一步推广到非均匀调和函数上才能更好地解决问题。
因此本文研究非均匀底空间微分算子的关系,建立非均匀调和函数与调和函数的关系,为进一步建立调和函数的积分理论提供重要的视角。
1 相关工作
在文献[2]中,作者们给出了非均匀解析函数定义以及一些微分刻画,随后在文献[3]中建立了关于非均匀解析函数的一些积分理论,并且给出了非均匀解析函数与非均匀调和函数关系的刻画。在文献[4]中,作者们利用高阶的非均匀Cauchy积分公式获得了非均匀Cauchy不等式,建立了关于非均匀解析函数的刘维尔定理。考虑到解析函数、调和函数它们之间相互联系的重要性,本论文利用一阶自变量算子之间的关系,进一步推广文献[4-10]中的解析函数相关内容,给出非均匀调和函数微分关系的刻画。最后,利用非均匀解析函数的平均值公式获得非均匀解析函数和关于非均匀调和函数的最大模原理,利用关于非均匀解析函数的刘维尔定理和非均匀解析函数与非均匀调和函数的关系,建立关于非均匀调和函数的刘维尔定理。最后将文献[11]的次调和函数推广到非均匀次调和函数,并建立非均匀次调和函数的性质。
2 预备知识
下面给出非均匀复数、非均匀复变函数的一些基本定义及性质,具体参考文献[2-3]。
2.1 非均匀复数的定义
考虑到复数在各个领域的广泛应用,我们对复数单位作进一步推广,定义非均匀复数。
定义集合Ck={z|z=x+jy},x,y∈R,j2=-k,k>0。
在Ck中引入数乘
z=x+jy,z∈Ck,m∈R,
mz=mx+jmy。
在Ck中引入加法
z1=x1+jy1,z2=x2+jy2,
(z1,z2∈Ck),
z1+z2=(x1+x2)+j(y1+y2)。
在上式数乘和加法运算下,Ck为线性空间,并且在上面的乘法运算,Ck还是一个域,我们称之为非均匀复数域。
2.2 非均匀复变函数的定义及性质
非均匀复变函数的定义,类似于复变函数的定义,形式上和数学分析中的函数定义相同,此时自变量和函数的取值均为新定义的非均匀复数。在定义函数之前,根据复平面点集的几个基本概念,我们给出非均匀复函数模的定义、三角表示和指数表示的定义。
设Ck是非均匀复数域,我们在Ck上定义非均匀模|z|k。
容易证明这样定义的模、三角不等式成立。并且有以下的三角表示和指数表示:
定义2.1由|z-z0|k<ρ所确定的非均匀平面点集(简称点集),就是以z0为圆心,以ρ为半径的非均匀圆,称为点z0的ρ-邻域。
注2.2考虑点集E,同样也有聚点(即极限点)、孤立点、外点、内点、闭集、开集、边界点、边界的概念,且与复变平面定义相同,在此不一一赘述。
定义2.3设f为从Ck到Ck的映射,则称f为Ck上的非均匀复函数。
定义2.4设函数w=f(z)在点z0的邻域内或者包含z0区域D时有定义,考虑比值

这时称非均匀复函数f(z)于点z0可导。
定义2.5若非均匀复函数w=f(z)在区域D内可微,则称f(z)为区域D内的解析函数,或称f(z)在区域D内解析。非均匀复函数在某点解析,是指在该点的某一个邻域内是解析的;函数在某个闭域解析,是指在包含该闭域的某区域内解析。
定理2.6[2]设f(z)=u(x,y)+jv(x,y)在区域D内解析,则:
1)偏微分ux、uy、vx、vy在区域D内连续;
2)u(x,y)、v(x,y)在区域D内满足非均匀C.-R.方程。
其中非均匀C.-R.方程为
这也是f(z)在区域D内可微的充要条件。
2.3 非均匀复变函数的积分
定义2.7设非均匀复数域Zk上的有向曲线C:z=z(t),(α≤t≤β)。
以a=z(α)为起点,b=z(β)为终点,f(z)沿C有定义,顺着C从a到b的方向在C上取分点a=z0,z1,…,zn-1,zn=b,这样可以将曲线C划分为n个弧段,在从zt-1到zt的每一个弧段上任取一点ξt,那么
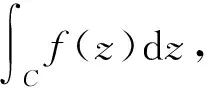
定理2.8[3]若f(z)=u(x,y)+jv(x,y)沿曲线C连续,则该函数沿曲线C可积,且
定理2.9[3]设有非均匀复数域Ck上的光滑曲线Cj:
z=z(t)=x(t)+jy(t),(α≤t≤β)。
z′(t)在[α,β]上连续且有不为零导数z′(t)=x′(t)+jy′(t),f(z)沿C连续,令f[z(t)]=u[x(t),y(t)]+jv[x(t),y(t)]=u(t)+jv(t),则
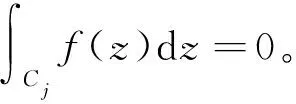
定理2.11[3]设f(z)在z平面上的单连通区域D内解析,则
定义的F(z)在D内解析,且F′(z)=f(z)。其中,z0为Ck上的固定点。
3 非均匀复解析函数的刻画

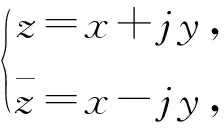
得
所以

(1)
(2)
定理3.1设f(z)=u(x,y)+jv(x,y),若u(x,y)、v(x,y)在区域D上可微,则
因此我们定义非均匀偏微分算子
证明:由二元实函数可微定义可得
由式(1)、(2),得
df=du+jdv
由
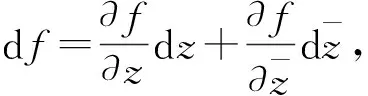
定理3.2设u(x,y)、v(x,y)在区域D上可微,则f(z)=u(x,y)+jv(x,y)在D内解析的充要条件是
证明:由定理2.6[2],我们仅需验证u(x,y)、v(x,y)满足非均匀C.-R.方程。由定义

可推出
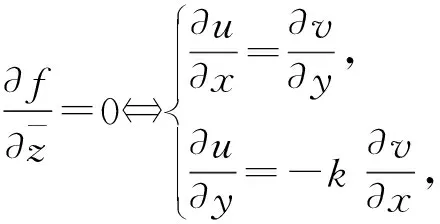

推论3.3设u(x,y)和v(x,y)在点z0=x0+jy0可微,则
f(z)=u(x,y)+jv(x,y)在z=z0可微的充要条件是
4 非均匀调和函数与非均匀共轭解析函数的关系
文献[3]已经给出了非均匀调和函数与非均匀共轭解析函数的关系,利用前面的导数关系进一步讨论它们之间的联系。
设非均匀复函数f(z)=u+jv在区域D内解析,非均匀C.-R.方程为
两等式两边分别对x、y求偏导,得
因在区域D内解析的非均匀复函数具有任意阶导数,所以在区域D内f(z)的实部u与虚部v都有二阶连续偏导数。由数学分析知识:因vxy、vyx在D内连续,他们必相等,故在区域D内有
同理:
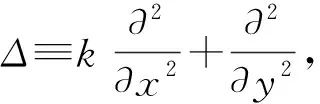
定义4.1[3]若二元实函数f(x,y)在区域D内有二阶连续偏导数,且满足非均匀Laplace方程Δf=0,则称f(x,y)为区域D内的非均匀调和函数。
定理4.2若二元实函数f(x,y)在区域D内二阶连续可微,且满足
则f(x,y)为D内的非均匀调和函数。
证明:
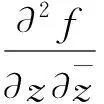

定义4.3[3]在区域D内满足非均匀C.-R.方程
的两个非均匀调和函数u、v中,v称为u在区域D的非均匀共轭调和函数。
注4.4由定理2.6[2]和上面的分析,我们发现:非均匀复函数f(z)=u+jv在区域D内解析,则u(x,y)、v(x,y)都是非均匀的调和函数,且v(x,y)是u(x,y)的非均匀共轭调和函数。易知,若u(x,y)、v(x,y)互为非均匀共轭调和函数,则它们必是常数。
定理4.5[3]设u(x,y)是单连通区域D内的非均匀调和函数,则一定存在u(x,y)的非均匀共轭调和函数v(x,y),即存在非均匀解析函数f(z)=u+jv。
5 非均匀平均值定理与非均匀极值原理
引理5.1(非均匀解析函数平均值定理) 若非均匀复函数f(z)在非均匀圆|ξ-z0|k 即f(z)在非均匀圆心z0的值等于它在非均匀圆周上的值的算术平均数。 定理5.2若非均匀复函数u(z)在非均匀圆|ξ-z0|k (3) 即u(z)在非均匀圆心z0的值等于它在非均匀圆周上的值的算术平均数。 证明:存在u(z)的非均匀共轭调和函数v(z),由定理4.5[3]:u(z)+jv(z)=f(z)在|ξ-z0|k u(z0)+jv(z0)=f(z0)= 即 比较两端的实部,并令r→R,即可得式(3)。 特别地,当z0=0时有公式 下面利用非均匀平均值定理讨论非均匀极值原理。 引理5.3(非均匀最大模定理) 若非均匀复函数f(z)在区域D内解析,且不为常数,则|f(z)|k在D内任意一点都不能达到最大值。 设M<+∞,因f(z)为非常数,所以0 G1={z∈D:|f(z)|k=M}, 显然G2是开集,现证G1是开集。设z0∈G1,则|f(z0)|k=M。因z0∈D,∃U(z0;δ)⊂D,由引理5.1知:当0 从而有 定理5.4设u(z)在单连通区域D内是非均匀调和函数,且不恒等于常数,则u(z)在D的内点处不能达到最值。 证明:用反证法证最大值的情况。设u(z)在单连通区域D内某点z0取到最大值,在单连通区域D内作与u(z)共轭的调和函数v(z),并记ef(z),则ef(z)在D内单值解析,且其模|ef(z)|k=eu(z)。此时,f(z)在点z0与u(z)一同达到最大值,与引理5.3矛盾,所以该定理最大值的情况得证。同理可证最小值的情况。 推论5.5 2)沿着边界C常有u(z)≤M,即如有u(z)非常数,则u(z)在D内不能达到最大值M,只能在边界上达到。 定理5.6若在整个平面上的非均匀调和函数u(z)有界,则u(z)恒为常数。 证明:由文献[4]的非均匀刘维尔定理知有界非均匀整函数f(z)必为常数,因为u(z)是在整个非均匀复平面上的非均匀调和函数,由文献[3],存在一个复函数f(z)=u+jv,使得它在整个平面上解析。因为Ref(z)≤M,不妨记F(z)=ef(z),则F(z)为非均匀整函数,又因为在非均匀复平面上|F(z)|k=eRef(z)≤eM,故有界。由非均匀刘维尔定理可得F(z)是常数,所以u(z)也是常数,定理5.6得证。 本节将文献[11]中的次调和函数定义及性质推广到非均匀次调和的情况,首先我们给出非均匀次调和函数的定义。 定义6.1设D是非均匀复数域Ck中的区域,若在区域D上的实值函数u(z):D→R∪{-∞}(u≢-∞)满足 1)u(z)上半连续; 由定义6.1我们可以知道每一个非均匀调和函数必定是非均匀次调和函数,所以非均匀次调和函数是比非均匀调和函数更为广泛的一类非均匀函数。 下面利用文献[11]的证明思想给出非均匀次调和函数的相关证明。 (4) 又因u和g分别是非均匀次调和函数和非均匀调和函数,所以有 于是有 u1(z0)=u(z0)-g(z0)≤ 即 这与式(4)矛盾,所以在G内有u(z)≤h(z)成立。 所以u是D上的非均匀次调和函数,得证。 下面我们利用和文献[11]类似的证明过程获得非均匀次调和函数的性质。 性质6.3设u是D上的非均匀次调和函数,θ是实数域上的增凸函数,则θ(u(z))也是D上的非均匀次调和函数。 又因θ是递增凸函数,所以 因而θ(u(z))也是非均匀次调和函数。 性质6.4设u是D上的次非均匀调和函数,对∀m≥0,m·u也是D上的非均匀次调和函数。 又因m≥0,所以 因而m·u也是非均匀次调和函数。 性质6.5设u1和u2是区域D上的非均匀次调和函数,对任意的λ1≥0,λ2≥0,λ1u1(z)+λ2u2(z)也是C上的非均匀次调和函数。 于是有 u(z0)=λ1u1(z0)+λ2u2(z0)≤ 因而λ1u1(z)+λ2u2(z)也是非均匀次调和函数。 例6.6设f(z)=u(x,y)+jv(x,y)在区域D内非均匀解析,则eλ1u+λ2v为D内的非均匀次调和函数,其中λ1,λ2≥0。 证明:由文献[3],u、v是D内的非均匀调和函数,由非均匀平均值公式可知u、v也是非均匀次调和函数,再由性质6.3和6.5,结论成立。 本文利用非均匀复数域空间微分算子的关系建立了调和方程的微分刻画,建立了非均匀调和函数与非均匀次调和函数的关系,获得了关于非均匀调和函数的刘维尔定理。本工作为进一步研究偏微分方程边值问题、积分核理论提供重要的理论基础。论文后续可以进一步研究非均匀解析函数的奇异积分理论,也可以研究Mobius群问题,例如:可以尝试将有关Mobius群交比方面的结论推广到非均匀解析函数。
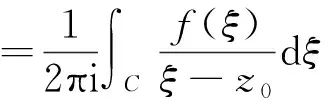
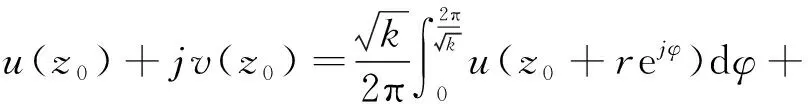
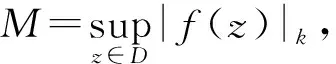
G2={z∈D:|f(z)|k

6 非均匀次调和函数定义及其性质



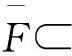


7 结 论
