巧用圆的性质 妙解解几问题

江苏省木渎高级中学 (320500) 解金雷

圆有许多几何性质，在解析几何问题求解中，常妙用圆的定义或性质，直径所对的圆周角为直角，圆幂定理，垂径定理，相交弦定理，切线长定理或切割线定理等实现解题的目的．本文列举几例予以说明.

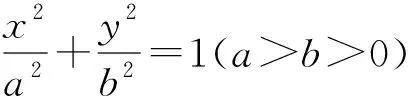
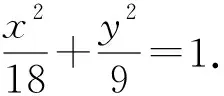
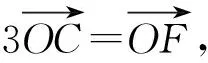
点评：解法中巧妙利用圆的切线性质及中点性质，并通过圆的定义确定对应圆方程，再利用二次方程的联立进而快捷确定相关点的坐标．

例2 已知圆x2+y2-6x=0，则过点(1，2)的直线被该圆所截得的弦的长度的最小值为( ).

A．1 B．2 C．3 D．4

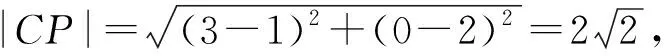
点评：本题为求解与圆的弦长有关的问题，而且是涉及与之相关的最值问题，求解的关键是利用圆的垂径定理达到将问题巧妙转化的目标．

例3 若直线y=kx+b(k>0)与圆x2+y2=1和圆(x-4)2+y2=1均相切，则k=，b=．

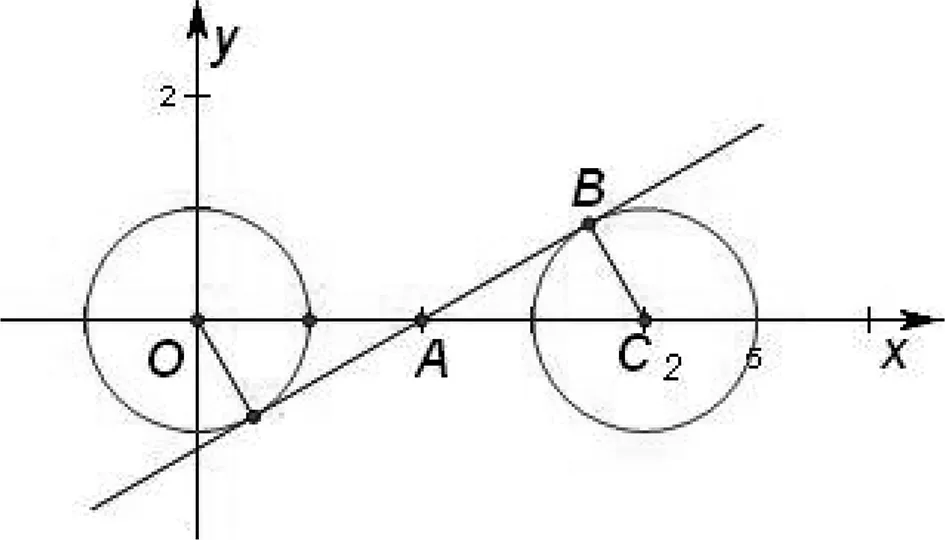
图1

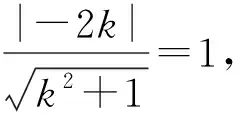
点评：本题巧用图形的几何性质，由“形”转“数”，综合推理与运算达到求解目标．

例4 已知⊙M：x2+y2-2x-2y-2=0，直线l：2x+y+2=0，P为l上的动点，过点P作⊙M的切线PA，PB，切点为A，B，当|PM|·|AB|最小时，直线AB的方程为( ).

A．2x-y-1=0 B．2x+y-1=0

C．2x-y+1=0 D．2x+y+1=0

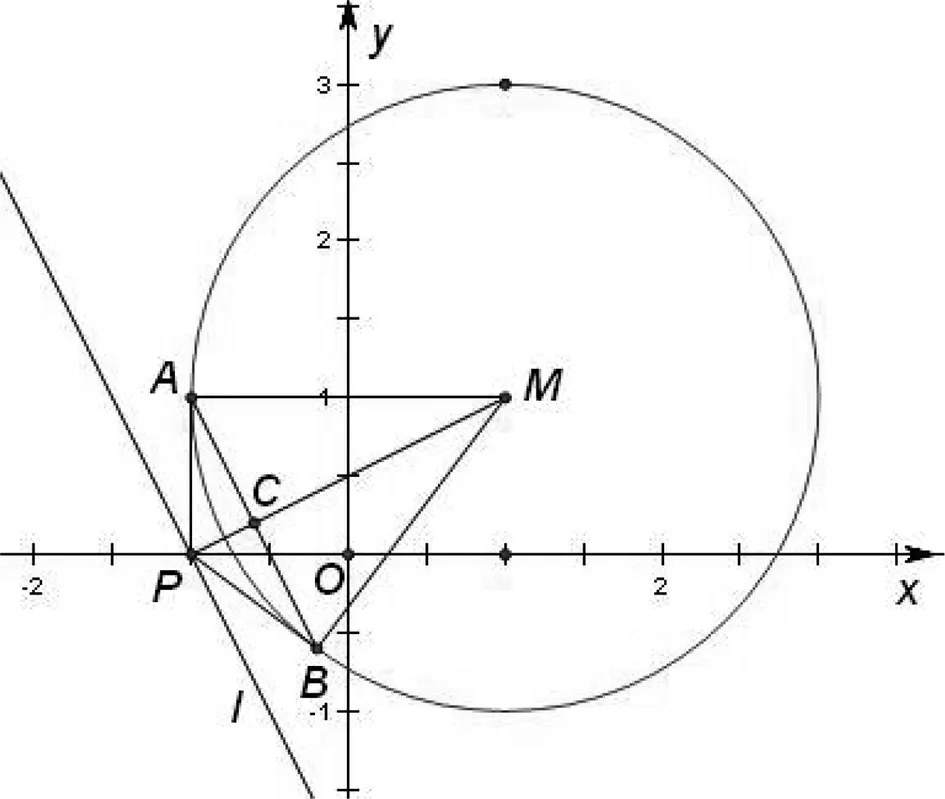
图2

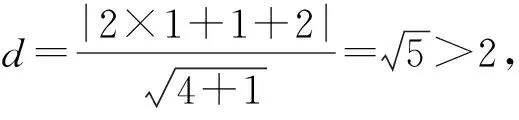
点评：本题综合利用圆的定义及几何性质，结合图形直观，化“动”为“静”，利用代数运算达到解决问题的目的．

综上可见，在解决一些与圆有关的解析几何问题时，巧用圆的平几性质，实现解几问题的直观化，达到多一些几何直观，少一些代数运算，“形”与“数”有机结合，从而有效发现解题思路，缩小思维步骤，优化解题过程，真正实现提升数学能力，培养核心素养的目标．