函数y=Asin(ωx+φ)性质的应用

江苏省泰州中学 (225300) 宋 健

关于函数y=Asin(ωx+φ)的图像和性质是三角知识的一个重要节点，从函数知识方面来说就是一个高点，关注与此有关的综合问题有助于全面理解课本知识体系，站在新的高度检验对这些知识点的掌握程度，本文通过分析几类典型题例的求解方法，展示此类问题的解题方案，务求给读者朋友有所帮助．

一、识图像 重应用

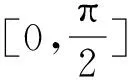
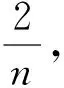
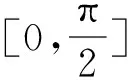
二、先转化 再化归

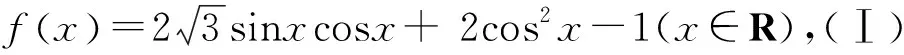
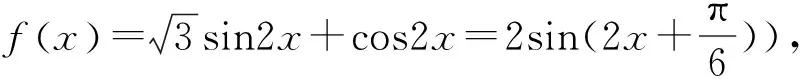
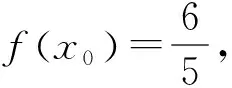
评注：这一类典型题目的解法是利用三角公式化简，将函数转化为y=Asin(ωx+φ)的形式，然后根据三角函数在特定区间上的有界性求出函数的最大值和最小值．

三、抓特点 定参数

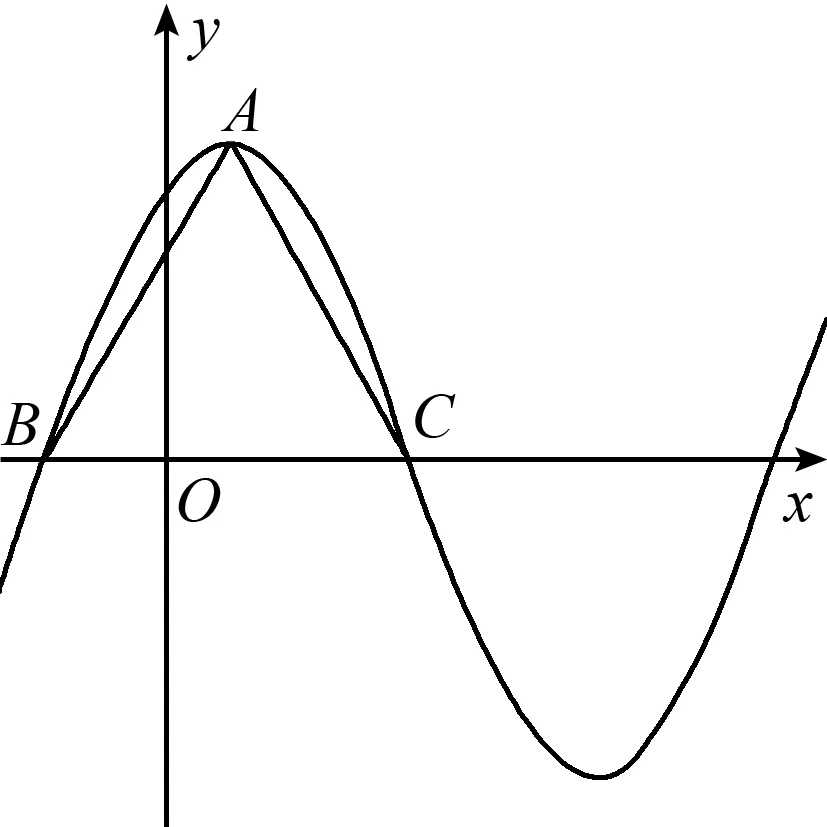
图1

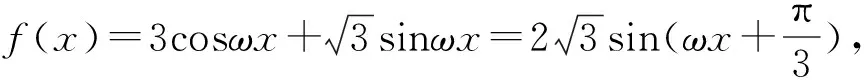
评注：在函数y=Asin(ωx+φ)中，如何根据已知条件确定其中的参数A、ω、φ，也是一类常见问题，这里必须抓住特点、精巧列式，本题中由正三角形的剖析是解题关键．

四、用性质 建方程

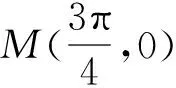
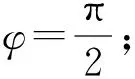
评注：本题的解决实际上是抓住两个对称性列方程、解方程的过程，由于三角函数有多值的特点，故需对参数k分类讨论，然后再逐个验证后确定，否则可能出现增解或漏解．

五、拟函数 再运用

例5 某港口水的深度y(m)是时间t(0≤t≤24，单位：h)的函数，记作y=f(t)，下表是某日的水深数据.

t03691215182124y10.013.09.97.010.013.010.17.010.0

经长期观察，这组数据比较稳定.(1)试根据以上数据，拟合函数拟合函数的近似表达式；(2)一般情况下，船舶航行时，船底离海底的距离为5 m或5 m以上被记为是安全的(船舶停靠时只需不碰海底即可)，某船吃水深度(船底离水平面的距离)为6.5 m，如果该船希望在同一天内安全进出港口，那么它至多能在港内停留多久？(忽略进出港所需时间)

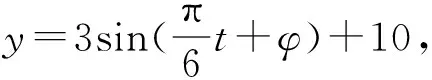
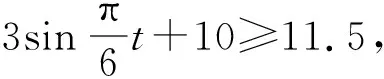
评注：本题是一个实际生活中的应用问题，由列表数据分析可得对应的函数图像是一个正弦曲线，抓住这个重要信息，拟合出函数解析式，为后面的实际问题的解决创造了条件．

六、综合题 抓主线

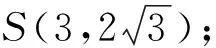
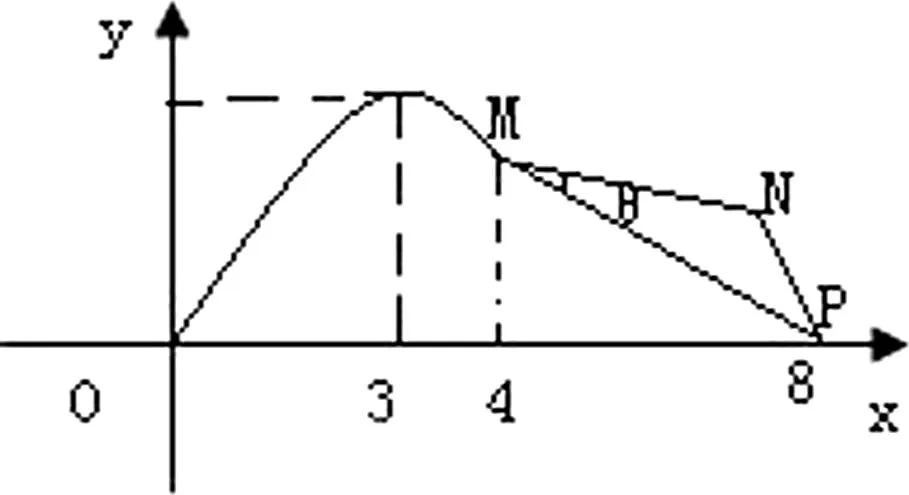
图2

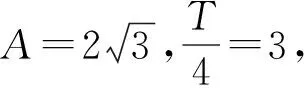
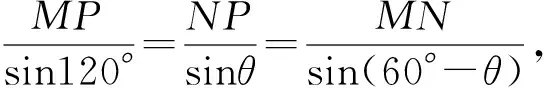
评注：本题是一道综合应用问题，先运用所给数据确定函数表达式，解决了关键的线段MP的长，然后再通过设∠PMN=θ，由正弦定理列式，建立了折线段赛道MNP的函数式，运用三角函数的有界性解决了最值问题，这就是此类题的求解主线．