破解数列问题中不定方程整数解的常用策略
2021-01-28江苏省昆山市教师发展中心215300峰江苏省昆山市柏庐高级中学215300何晓勤
江苏省昆山市教师发展中心 (215300) 戈 峰江苏省昆山市柏庐高级中学 (215300) 何晓勤
在数列综合问题中,经常会遇到不定方程的整数解问题,此类问题往往会涉及函数、方程、不等式、数列的性质及数论等知识,精彩纷呈,解法灵活多样.因此,探讨求解此类问题的常用策略很有必要.所谓不定方程的整数解问题是指方程的个数小于未知数的个数,且未知数的解为整数的问题.笔者下面通过举例,谈谈求解数列存在性问题中不定方程整数解的常用策略,供大家参考.
1.整除分析法
利用数列项数为正整数这一特性,可将不定方程中的某个变元用其他变元代数表示,并分离常数(整数),再利用整除的性质分析方程的整数解.
例1 设数列{an}是公差为2的等差数列,数列{bn}满足b1=1,b2=2,anbn+bn=(n+1)bn+1.
(1)求数列{an}和{bn}的通项公式;
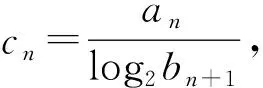
解析:(1)在anbn+bn=(n+1)bn+1中,令n=1,得a1=3,所以an=3+2(n-1)=2n+1.将an=2n+1代入anbn+bn=(n+1)bn+1,得bn+1=2bn,所以数列{bn}是以1为首项,2为公比的等比数列,即bn=2n-1.
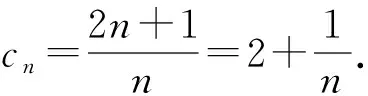
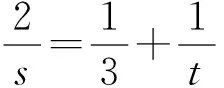
2.奇偶分析法
对于某些不定方程,可从不定方程等式两边的符号和奇偶性角度分析,寻求矛盾来否定存在性,或构造等量关系来肯定存在性.
例2 已知数列{an}的前n项和为Sn,满足Sn=2an-1(n∈N*),数列{bn}满足nbn+1-(n+1)bn=n(n+1)(n∈N*),且b1=1.
(1)求数列{an}和{bn}的通项公式;
(2)是否存在正整数m,n,使b1,am,bn(n>1)成等差数列?若存在,求出所有满足条件的m,n;若不存在,请说明理由.
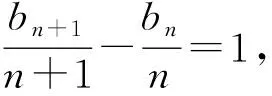
(2)假设存在正整数m,n(n>1),使b1,am,bn成等差数列,则b1+bn=2am,即1+n2=2m.若n为偶数,则1+n2为奇数,而2m为偶数,上式不成立.若n为奇数,设n=2k-1(k∈N*),则1+n2=1+(2k-1)2=4k2-4k+2=2m,于是2k2-2k+1=2m-1,即2(k2-k)+1=2m-1.当m=1时,k=1,此时n=2k-1=1与n>1矛盾;当m≥2时,上式左边为奇数,右边为偶数,显然不成立.
综上所述,满足条件的正整数m,n不存在.
总结:本题破解的关键是运用奇偶分析法研究方程1+n2=2m的正整数解的情况.在正整数中,奇数与偶数不等是基本矛盾之一,通常可以用来说明不定方程的整数解不存在.
3.因式分解法
若不定方程可化为一边是两个(或多个)因式的乘积,另一边是一个整数的形式,则可因式分解后分析不定方程的整数解的情况.

(1)求数列{an}的通项公式;
(2)是否存在大于2的正整数m、k,使得am+am+1+am+2+…+am+k=300?若存在,求出所有符合条件的m、k;若不存在,请说明理由.

(2)存在大于2的正整数m、k,使得am+am+1+am+2+…+am+k=300.
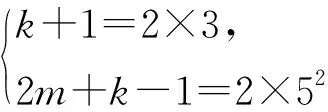
总结:本题求解的关键在于因式分解得到am+am+1+am+2+…+am+k=(2m+k-1)(k+1)及300=22×3×52,再结合奇偶性和整除性处理.处理此类问题时,往往需要对分解所得的因式的大小、奇偶、正负等进行讨论,以减小运算量.
4 不等关系转化法
若不定方程中涉及的多个变量有范围或大小关系时,可通过不等关系的转化将其中一个变量的范围缩小,从而求出这个变量的整数解,再进一步求出其他变量的整数解.
例4 已知等差数列{an}的前n项和为Sn,a2+a5=12,S4=16.
(1)求{an}的通项公式;
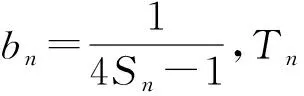
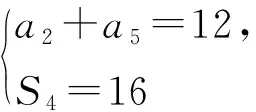
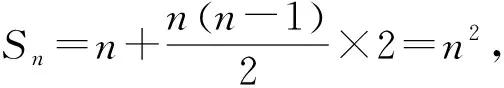
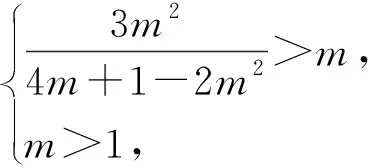
故存在m=2,k=12满足题意.
总结:在多变量中,往往需要紧扣多个变量之间的大小关系(比如本题中的k>m)以及变量自身内含的范围(比如本题中的m是大于1的正整数),其中一个变量对另一个变量的取值范围起着决定性作用.当不定方程的整数解较难确定时,可利用不等式前后夹逼的方法得到整数解.
5.单调性分析法
数列是特殊的函数,可利用其单调性来研究不定方程的正整数解问题.求解时,常将不定方程两边都看作一个以某变量为主的数列(或函数),再分别研究这两个数列(或函数)的单调性.
例5 已知数列{an}与{bn}的前n项和分别为An和Bn,且对任意n∈N*,an+1-an=2(bn+1-bn)恒成立.
(1)若An=n2,b1=2,求Bn;
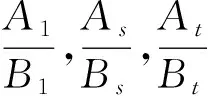
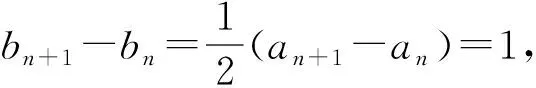
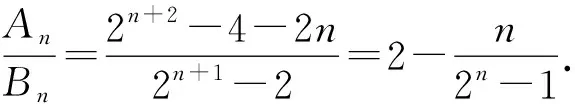
总结:研究数列的单调性主要有作差法(即利用定义)或者构造函数(注意需要将定义域扩充为连续区间),利用函数的性质或导数法处理.一般地,单调数列可确定数列的范围,进而可确定方程是否有解.
6 基本不等式法
对于某些不定方程,可借助基本不等式导出矛盾,从而说明其正整数解不存在.
例6 已知数列{an}的前n项和Sn满足2Sn=3(an-1)(n∈N*).
(1)求数列{an}的通项公式;
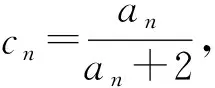
解析:(1)因为数列{an}的前n项和Sn满足2Sn=3(an-1)(n∈N*),所以当n≥2时,2Sn-1=3(an-1-1),两式相减得2an=3an-3an-1,即an=3an-1(n≥2),又n=1时,2S1=3(a1-1),解得a1=3≠0,所以数列{an}是以3为首项,3为公比的等比数列,从而an=3n.
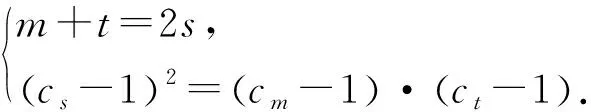
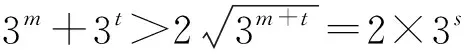
7.有(无)理数定义法
若不定方程中涉及无理数,应考虑利用无理数和有理数的定义处理.
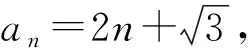
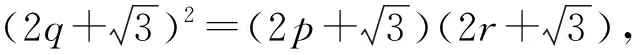
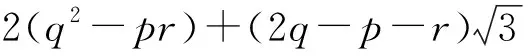
以上仅列举了求解数列问题中不定方程整数解的七种常用策略,对于具体问题还需具体分析,灵活处理,做到以不变应万变.
