一道三诊试题的多解及推广
2021-01-28四川师范大学数学科学学院610068纪定春夏逸天周思波
中学数学研究(江西) 2021年2期
四川师范大学数学科学学院 (610068) 纪定春 夏逸天 周思波
不等式是高考数学的重点考察内容.从作差法、判别式法、三元均值不等式法、基本不等式法、柯西不等式法、排序不等式法、几何法、向量法、权方和不等式法、詹森不等式法、球坐标变换法、拉格朗日乘数法等角度,对四川省泸州市三诊的一道不等式试题进行了解法探究,并将该不等式进行了推广.
1.问题与评注
(泸州市高2017级第三次教学质量诊断性考试)已知f(x)=|2x-4|+|x+1|.

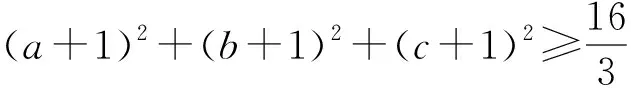
2.解法探究
视角1 作差法
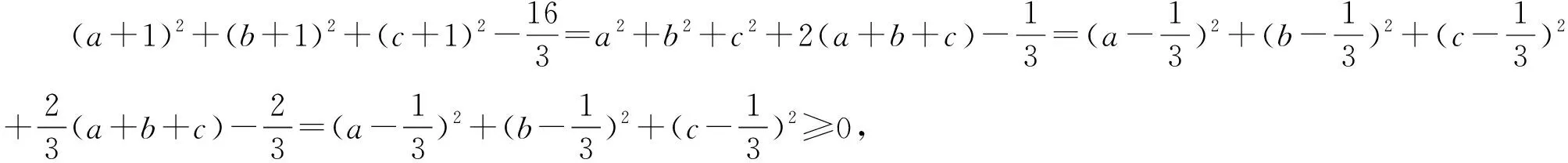
视角2 判别式法

视角3 三元均值不等式法

视角4 基本不等式法

视角5 柯西不等式法
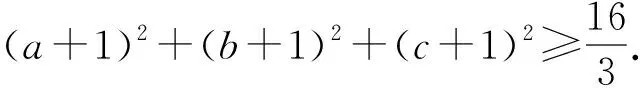
视角6 排序不等式法
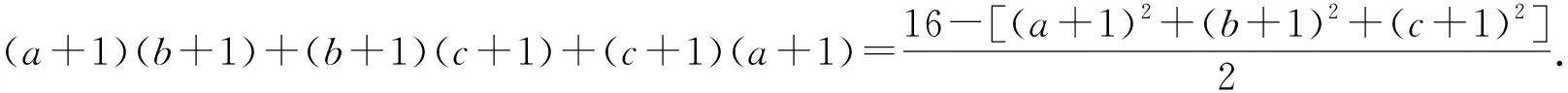
所以(a+1)2+(b+1)2+(c+1)2≥
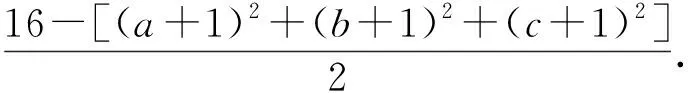
视角7 几何法
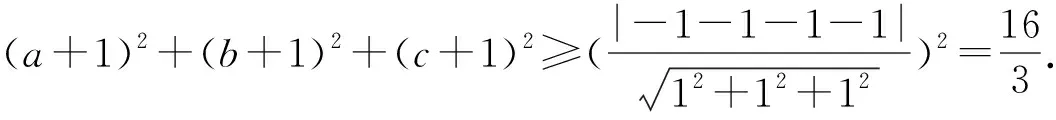
视角8 向量法
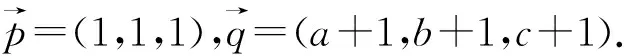
视角9 权方和不等式法
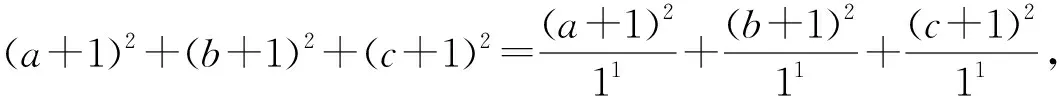
视角10 詹森不等式法
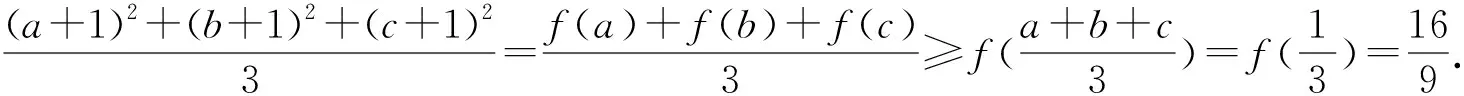
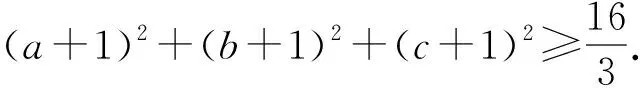
视角11 球坐标变换法
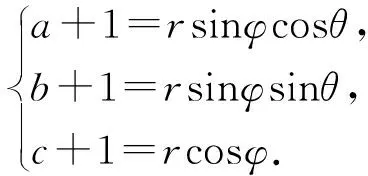
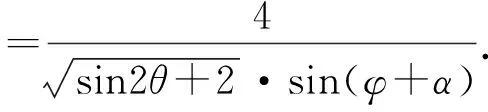
视角12 拉格朗日乘数法

3.问题推广
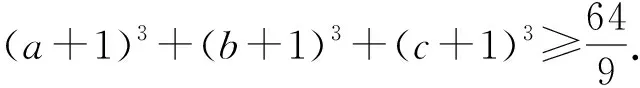
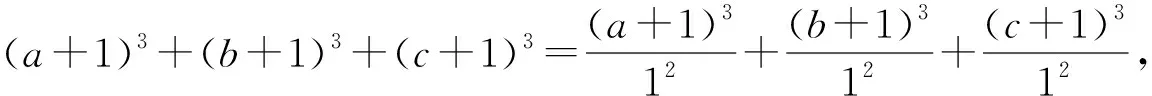

推广3 设a,b,c∈R,且a+b+c=s,其中n∈Z+,x,y,z为任意的常数,求(a+x)n+(b+y)n+(c+z)n的最小值.
提示:推广2和推广3,解决方法同推广1.

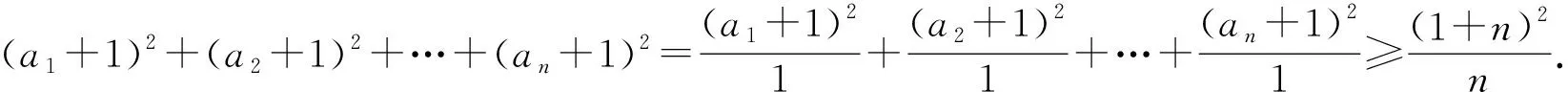
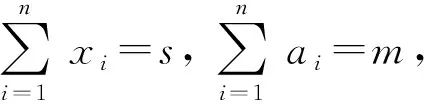

提示:推广5和推广6,解决方法同推广4.
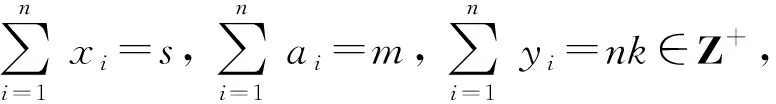
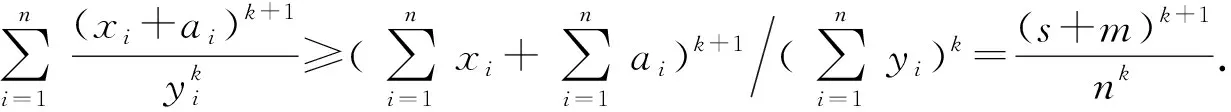

提示:该推广,将项(-1)i引入了第i个项中,求解过程更加复杂.在求解时,需要注意进行分类讨论,此处可以分成四类,然后分别进行讨论,最终求解结果为三大类.
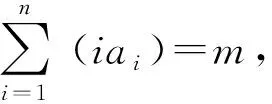
解决过程可参照推广7,注意使用换元法,具体从略.最后,由于推广8、推广9较难,建议不将两个推广纳入高中数学课堂,但可以作为课后自主思考题.上述的推广1-7,可以根据所教学生的实际情况,有选择的纳入课堂.
