对一组优美几何不等式的推广
2021-01-28浙江大学附属中学丁兰校区310021陈作国施刚良
中学数学研究(江西) 2021年2期
浙江大学附属中学丁兰校区 (310021) 陈作国 施刚良
在△ABC中,设△ABC的面积为S,角A,B,C所对的边分别为a,b,c,则有下列不等式链:
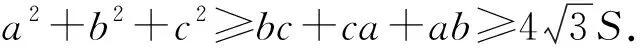
笔者仔细研究了文[1]的证明过程,发现可以改进方法,将结论推广如下:
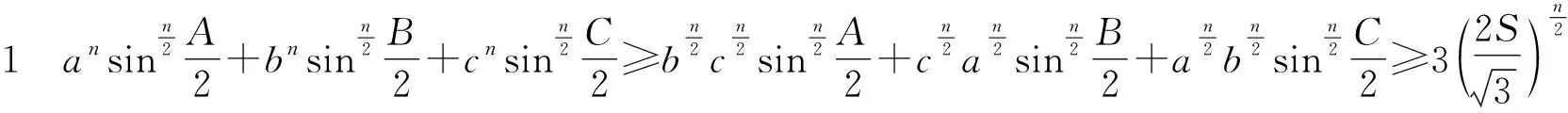
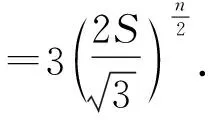
当n=2时,即不等式②.同时,还对①进行了推广可得:
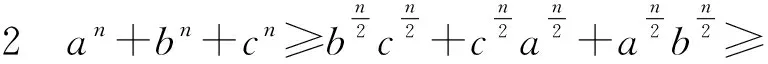
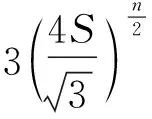
当n=2时,即得到不等式链①.
要证明定理1和定理2,先引进如下引理:
引理1 在△ABC中,恒有
引理2 在△ABC中,恒有
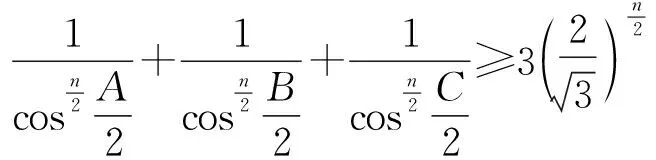
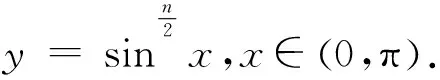
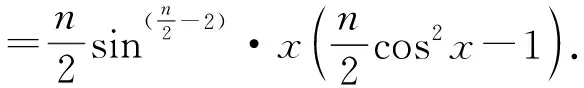
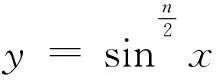
引理2的证明:与引理1的证明类似,在此不再叙述.
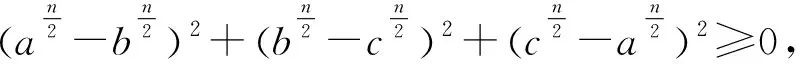
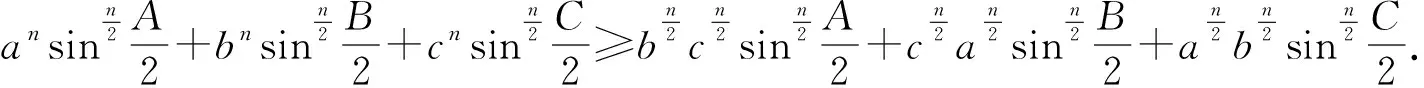
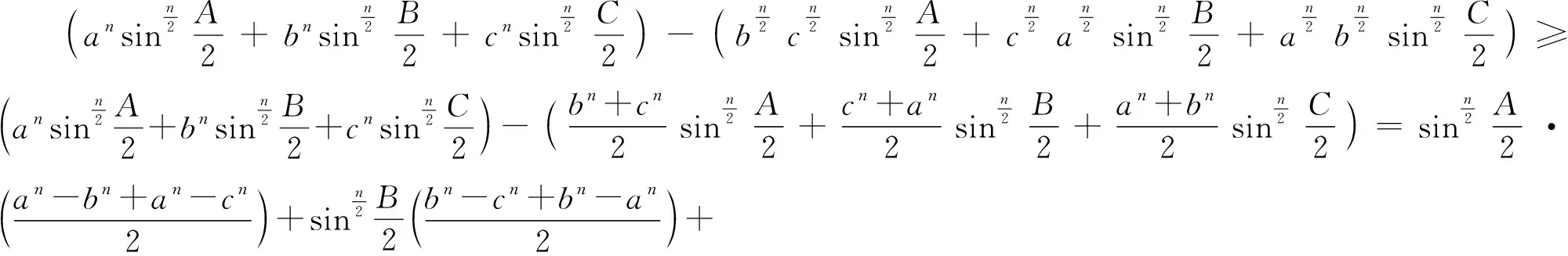
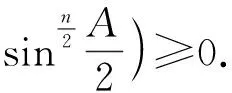
结束语
初等数学中的不等式问题是中学数学教师研究的热门问题,一般比较容易上手,但要深入进去往往又非常困难,这真是不等式问题的魅力所在.再之,本文对文[1]结论作了推广,在论证一般性结论时,发现初等的方法已不够,于是借用函数的凹凸性,发现证明变得相对容易,体现研究初等数学问题的高观点.本文推广的结论只对0≤n≤2成立;当n>2时,笔者试着利用函数的凹凸性没法解决,也就是说高观点也是有局限性的,可能利用初等的方法反而能解决.这也体现出不等式问题的灵活性和技巧性,体现不等式的魅力.当n>2时,结论是否还成立,留给有兴趣的读者.
