一道指对混合型不等式高考题的解法探究*
2021-01-28新疆乌鲁木齐市实验学校830026符强如新疆乌鲁木齐市第97中学830022雷高龙
新疆乌鲁木齐市实验学校 (830026) 符强如新疆乌鲁木齐市第97中学 (830022) 雷高龙
纵观近几年的高考导数压轴题,其中一类指数、对数混合型求参数的取值范围综合问题处理起来比较棘手,也具有较强的区分度.下面就以一道高考导数真题来具体阐述笔者的思考.
1 问题呈现及背景
题目已知函数f(x)=aex-1-lnx+lna.
(1)略;(2)若f(x)≥1,求a的取值范围.
背景:这道题是2020年新高考全国卷理数21题,从问题表述来看,传承了全国卷高考命题朴实、简约、稳健的风格.从函数的角度考察指数、对数混合型问题.而现阶段以指数函数与对数函数为载体的导数与含参恒成立求解参数范围问题,在高考压轴题中频繁出现,它不仅考查了考生的逻辑推理、数学建模、数学运算等核心素养,并对要求考生具备较高的思维能力,不愧起到了压轴的功能.
2 多个视角探究
视角1:直接构造
证明函数不等式恒成立的首选方法就是直接构造,也是师生在解题过程中最常用的方法.由于恒成立的不等式中同时含有指数函数和对数函数,所求构造函数的最值往往涉及到导函数零点问题存在却不易求解情况,一般可选择设而不求,整体代换化简的思路,即隐零点问题处理策略,有时还会涉及到放缩.
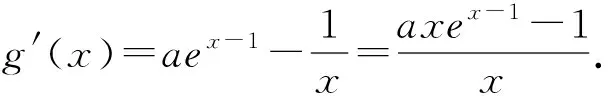
视角2:放缩
改头换面进行合情合理放缩.在使用放缩法时要注意把握放大或缩小的度.常见的指对函数放缩来源于人教A版数学选修2-2第32页B组第一题,即ex≥x+1,x-1≥lnx.此题可将ex,lnx同时改头换面放缩成直线,就可比较快速解决.
设g(x)=ex-x+1,g′(x)=ex-1,易得g(x)在(-∞,0)上单调减,在(0,+∞)上单调增,故g(x)mix=g(0)=0,∴ex≥x+1,由两边同时取对数可得x≥ln(x+1),易得x-1≥lnx.由ex≥x+1可得aex-1=elna+x-1≥lna+x-1+1,由x-1≥lnx可得-lnx≥1-x.故f(x)≥lna+x-1+1+1-x+lna,(当x=1时取等号).∵f(x)≥1,∴2lna+1≥1,∴a≥1.
也可以从这个角度去放缩由ex≥x+1可得aex-1≥ax,由x-1≥lnx可得-lnx≥1-x.∵f(x)=aex-1-lnx+lna≥1,∴ax-x+1+lna≥1,∴(a-1)x≥-lna恒成立.当0 视角3:指对分离分而治之 指对分离分而治之是将对数式和指数式分离成两个独立的函数,分别求最值即可,为方便计算,我们一般分离构造的两个独立函数的“凹凸性”是相反的,利用公切线作为两曲线的分界线,就将复杂的指对混合型不等式转化为两个简单的不等式.值得一提的是有时分离的两个函数不存在最值时还需要适当变形. 视角4:指对互化换元构造 有些指对混合型的不等式中不仅存在x+lnx还存在xex,此时可以利用指对恒等式x=elnx将x+lnx=ln(xex),xex=ex+lnx转换为只含有xex或x+lnx问题,再进行构造函数快速解决.由题f(x)≥1可得aex-1-lnx+lna≥1恒成立,∴elnaex-1+lna+x-1≥lnx+x.∴elna+x-1+lna+x-1≥elnx+lnx成立.故可构造h(x)=x+ex,h′(x)=ex+1>0,∴h(x)在x∈R上单调增.易得h(lna+x-1)≥h(lnx),∴lna≥lnx-x+1,由x-1≥lnx易得lna≥0,∴a≥1. 也可如下构造:由题可得aex-1-lnx+lna≥1,∴elna+x-1-(lna+x-1)-1+(x-lnx-1)≥-2lna可构造函数,易得h(x)=ex-x-1,易得h(x)min=0,故可得-2lna≤0,∴a≥1. 评注:不同的表征形式其求解着眼点就有不同,其求解思路切入各有其特征、使用的范围和求解步骤.因其求解的思路与着眼点相同,所以表现出得解题过程难易程度就有深有浅.角度1:对隐零点的范围判断是一个难点,本文从极限角度出发判断零点的存在;角度2:改头换面进行放缩,虽然有时很简捷但却具有一定的局限性;角度3:需要敏锐的眼光,才能找到凹凸性不同的两个函数,选择分离指对函数分而治之去解决;角度4:通过指对恒等式变形后能较好找到构造的函数再根据单调性去解决. 平时我们的解题教学,利用所有有用的条件,进行观察、联想、对比,采取“一题多解”的形式,不仅能使同学们的思维定势得到改观,还可以使所学的知识得到到灵活运用,进而开拓思路,这对培养学生思维的广阔性、探索性、深刻性、独创性、灵活性等无疑是一条非常有效的捷径.作为教师也有必要为学生的知识延伸和深度做指导,唯有如此,我们的复习才能真正优质高效,学生认知结构才能更加稳定,数学核心素养的培育才能深入落实.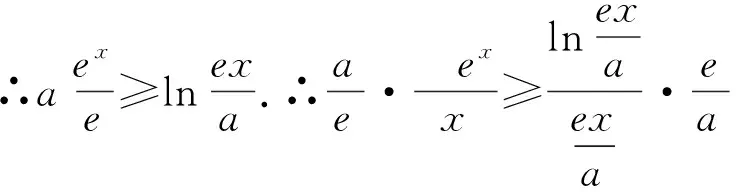

3 解题反思
