利用最小二乘支持向量机的短临降雨预测模型构建

2021-01-27赵庆志姚顽强

大地测量与地球动力学 2021年2期

赵庆志刘洋姚顽强

1 西安科技大学测绘科学与技术学院，西安市雁塔路58号，710054

降雨的发生受多种气象变量、位置和季节的影响[1]，近年来，基于GNSS技术反演PWV并研究其与降雨间的相关关系逐渐发展成为新的研究领域，一些学者根据降雨发生前PWV的异常变化特征，构建基于最小二乘法的简单短临降雨预测模型，以描述PWV与降雨间的相互关系[2-4]。

支持向量机(SVM)的相似版本——最小二乘支持向量机(LS-SVM)由Suykens等于1999年提出。SVM算法需要不敏感损失函数ε来解决特征空间中的凸二次规划问题，而LS-SVM仅需最小二乘损失函数以获取高维空间中一组线性等式，进而提高学习速率并降低SVM中凸规划的复杂度。此外，相比于SVM算法中惩罚参数、核参数sig2及不敏感损失函数ε等3种关键参数复杂的选取策略，LS-SVM仅需确定正则参数gam及径向基函数(RBF)参数sig2即可构建相应模型[5]。LS-SVM算法已成为一种解决非线性分类、函数估计及回归的重要理论，并被应用于多种学科[6-7]。

传统的简单降雨预测模型基于最小二乘原理拟合PWV/ZTD时变信息，以预测未来短期内发生的降雨事件。该类降雨预测模型普遍存在的缺陷是：1)降雨预测因子(PWV/ZTD)单一；2)降雨预测精度较低，预测正确率仅为80%，错报率介于60～70%之间[2-4]。因此，本文首次将LS-SVM算法用于构建短临降雨预测模型，将多种与降雨相关的气象参数添加进训练样本，并分别从以上两个方面改进传统降雨预测模型。

1 理论和数据

1.1 GNSS获取PWV

GNSS信号穿过对流层时会受中性大气延迟效应的影响，测站天顶总延迟(ZTD)可由信号倾斜路径总延迟(STD)通过映射函数投影至天顶方向得到。本文使用全球投影函数(GMF)将不同高度角的卫星信号投影至GNSS测站天顶方向，并忽略测站卫星信号弯曲的影响[8]。

ZTD主要由天顶静力延迟(ZHD)和天顶湿延迟(ZWD)组成[9]，其中ZHD可通过saastamoinen模型求解。ZTD与ZHD之差即为ZWD，PWV与ZWD之间的转换公式为：

(1)

式中，ρ为液态水密度；ξ为PWV和ZWD之间的转换参数[10]：

ξ=[-1×SGN(L)×1.7×10-5|L|HSN-

[0.165-(1.7×10-5)|L|1.65]+R

(2)

式中，L为测站纬度；doy为年积日。当GNSS测站位于南/北半球时，HSN分别为1.25和1.48，SGN(L)分别为-1和1。通过式(1)和式(2)，可计算精度在±1 mm范围内的PWV时间序列[10]。

1.2 最小二乘支持向量机

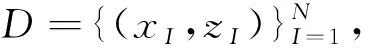
z(x)=wTϑ(x)+b

(3)

式中，w为权重向量；ϑ(·)为投影函数；b为阈值。将回归等式转化为最小化代价函数约束的优化问题：

(4)

式中，δ为正则化参数，作用为平衡模型的复杂性和精度；ξI为输入向量xI的训练误差。式(4)对应的约束条件为：

zI=wTϑ(xI)+b+ξI，I=1,2,…,N

(5)

与SVM不同的是，LS-SVM使用等式约束而非不等式约束。基于上述等式，拉格朗日函数可表示为：

(6)

式中，αI为拉格朗日乘子。函数逼近模型为：

(7)

式中，K(x,xI)为核函数，本文使用径向基函数。

1.3 数据简述

选取南洋理工大学和新加坡国立大学2个GNSS并址气象站(NTUS和SNUS)2010～2012年的数据，其中GNSS数据经GIPSY/ OASIS Ⅱ 处理得到ZTD数据[11]，ZHD数据经saastamoinen经验模型计算得到，PWV数据经式(1)计算得到。NTUS站气象数据有温度(T)、相对湿度(RH)、露点温度(DPT)，SNUS站气象数据有气压(P)、温度(T)、相对湿度(RH)。此外，新加坡地区的降雨主要受季节影响，大多发生在东北雨季及西南雨季期间，强对流型降雨出现在东北雨季的傍晚时段。因此，本文考虑将年积日(doy)和天积时(hod)作为与降雨相关的时间参数。

2 气象参数特征分析

2.1 参数时序分析

降雨的发生受多种气象参数的影响，选择与降雨相关性高、易获取的气象参数对构建精度高、适用性强的LS-SVM降雨预测模型有很大帮助。图1和2分别为NTUS站和SNUS站降雨及其相关气象参数的时变序列。由图可知，降雨发生前，PWV、RH、P及T都出现上升趋势；降雨发生时都表现出下降的趋势，且T的下降速率及幅度均大于PWV；而RH在降雨发生时表现出上升的趋势，DPT则表现出与之相反的变化趋势。

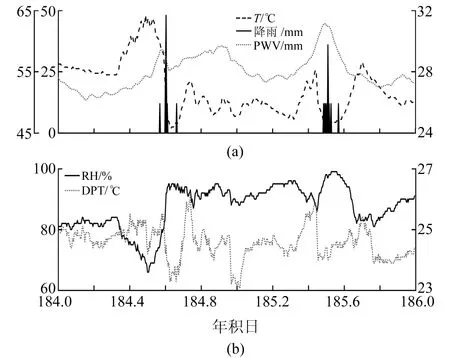
图1 NTUS站2012年doy184～186降雨及其相关气象参数的时变序列Fig.1 The time series of rainfall and its correlated meteorological parameters at NTUS station over the period of doy 184-186 in 2012

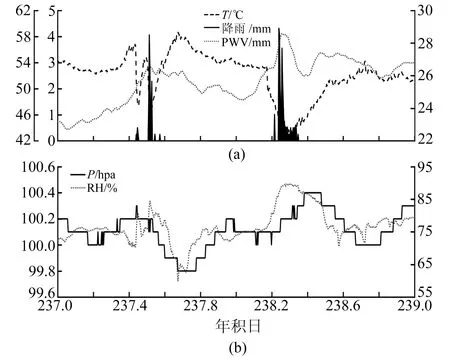
图2 SNUS站2011年doy237～239降雨及其相关气象参数的时变序列Fig.2 The time series of rainfall and its correlated meteorological parameters at SNUS station over the period of doy 237-239 in 2011

2.2 相关性特征分析

图3为2010～2012年2个测站降雨及多种参数(doy、hod、T、DPT、RH、PWV)的相关系数示意图，可以看出，NTUS站中T和RH表现出强负相关特征，相关系数为-0.89；T和DPT的相关系数为0.5，表现出中等正相关特征；DPT和doy、RH和PWV及T和hod都表现出弱正相关特征，相关系数约为0.3。此外，降雨与气象参数间并无弱及以上相关性特征，表明降雨与本文所选气象参数相关性较弱，还可能与其他气象参数相关。同时PWV与降雨并未表现出强相关性特征，表明传统降雨预测模型仅依靠PWV不能达到构建高精度降雨预测模型的目的。

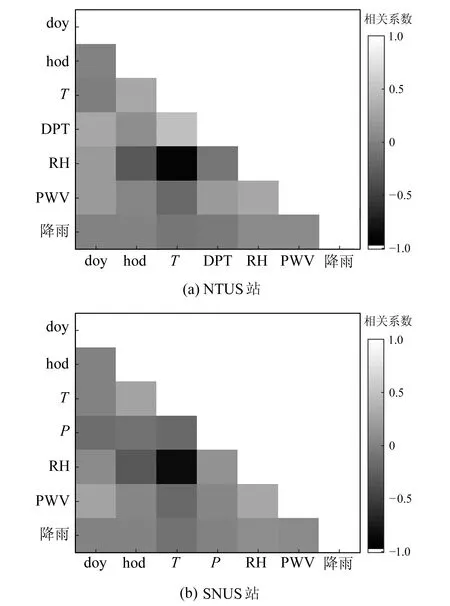
图3 气象参数、时间参数与降雨间相关系数示意图Fig.3 Correlation coefficient between rainfall and meteorological parameters, time parameters

3 基于LS-SVM的降雨预测

3.1 实验流程设计

LS-SVM降雨预测的实验流程主要分为模型构建、仿真实验和预测实验3个部分。1)模型构建：首先对训练数据进行均衡处理和归一化处理，同时对缺失数据进行删除。设置决定LS-SVM模型精度的正则化参数gam及RBF核参数sig2的范围，在将训练数据样本输入LS-SVM模型之前需要将降雨数据和PWV/气象数据分开并设置时差为55 min，目的是构建当前PWV/气象数据与未来55 min降雨事件间的高维非线性关系(基于LS-SVM模型)。由于大多数降雨持续时间超过35 min，因此降雨预测时间区间扩展为未来20～90 min。最后将训练样本输入LS-SVM模型进行训练，并基于网格搜索法和交叉验证法对参数进行寻优，得到基于LS-SVM的短临降雨预测模型。2)仿真实验：对训练数据进行归一化处理，并输入LS-SVM降雨预测模型得到仿真降雨数据，根据正确率(TFR)和错报率(FFR)评估仿真降雨数据与实际降雨数据间的吻合度。3)预测实验：将次年数据进行归一化处理后输入LS-SVM降雨预测模型，得到次年预测降雨数据，并根据TFR和FFR两个指标评估预测结果的精度。

3.2 数据预处理

当多数类样本数据占样本数据的比例远大于少数类样本数据时，分类器可预测样本中多数类样本数据而完全忽略少数类样本数据[10]。图4统计了NTUS站和SNUS站2010～2012年降雨类数据和非降雨类数据的数目后发现，二者的均值比例为1∶39，表明降雨类事件与非降雨类事件存在严重失衡的特征[12]。利用降采样方法得到相同数目的降雨类数据和非降雨类数据[13]，并将二者组合为训练数据集。

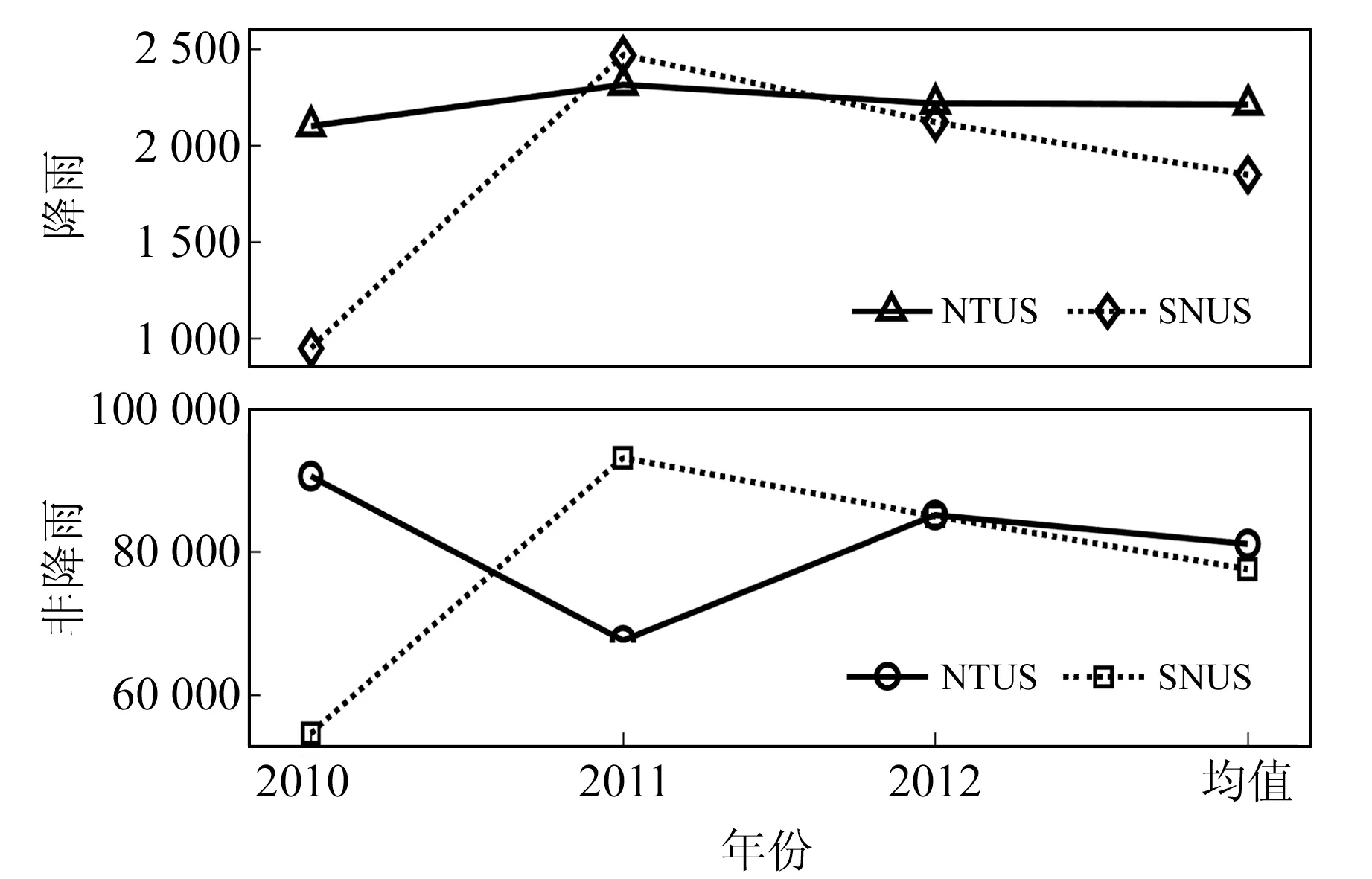
图4 NTUS站和SNUS站降雨及非降雨数据Fig.4 The schematic diagram of rainfalland non-rainfall data at NTUS and SNUS stations

3.3 仿真实验

以NTUS站2010年仿真实验为例，首先利用降采样方法对气象和时间参数进行均衡化及归一化处理。正则化参数δ/gam和RBF核函数ϖ/sig2对LS-SVM模型的精度起着关键性作用，本文基于网格搜索法和交叉验证法确定δ/gam和ϖ/sig2的最优值。其次将6种预报因子(doy、hod、T、DPT、RH、PWV)与降雨数据输入LS-SVM模型进行训练，得到LS-SVM降雨预测模型。最后将6种气象数据经归一化后输入LS-SVM降雨预测模型，得到NTUS站2010年降雨仿真结果。SNUS站的仿真实验流程与上述流程一致。

本文使用正确率(TFR)和错报率(FFR)来评估LS-SVM降雨预测模型的精度：

(8)

式中，Nt为正确预报降雨次数，即预测降雨时段内实际发生的降雨次数；Nf为错误预报降雨次数，即预报时段内实际未发生降雨的次数；Nreal为实际发生的降雨次数。

图5为SNUS站和NTUS站2010～2011年降雨仿真结果，由图可见，2个测站的降雨仿真TFR均接近100%，而SNUS站2010年和2011年的FFR均大约为44%，NTUS站2010年的FFR为53%，2011年的FFR为31%。综上所述，SNUS站和NTUS站在2010～2011年的降雨仿真TFR均值为99.94%，FFR均值为43%。结果表明，LS-SVM模型可仿真1 a中所有的降雨事件，且错报率低于传统降雨预测模型，可用于预测2011～2012年的降雨事件。

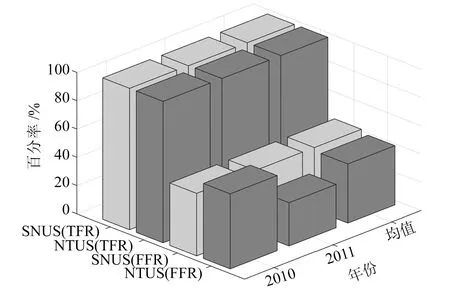
图5 NTUS站和SNUS站2010～2011年降雨仿真实验结果Fig.5 The simulated experimental results of rainfall atNTUS and SNUS stations over the period of 2010-2011

3.4 预测实验

以NTUS站2011年预测实验为例，首先对6种数据进行归一化处理，将数据输入仿真实验LS-SVM降雨预测模型中得到降雨预测数据，再根据TFR和FFR对数据精度进行评估。SNUS站的预测实验流程与该流程一致。

图6为SNUS站和NTUS站2011～2012年降雨预测结果，由图可见，2个测站的降雨预测TFR相近，均接近100%；SNUS站与NTUS站2011年的FFR均小于40%，2012年FFR分别为42.58%和45.79%。综上可知，SNUS站与NTUS站在2011～2012年的降雨预测TFR均值为99.57%，FFR均值为40.42%。因此，本文基于LS-SVM的短临降雨预测模型可预测未来20～90 min内99%的降雨事件，且FFR为40%。与最小二乘线性降雨预测模型相比，本文模型预测结果的TFR提高近10%，FFR降低近20%。