应用分块矩阵求逆解算约束秩亏间接平差模型
2021-01-27刘连旺
谢 波 刘连旺
1 合肥职业技术学院建筑工程学院,合肥市姥山南路1号,238000 2 桂林理工大学博文管理学院,桂林市雁山街317号,541006
在经典测量平差模型中,将附有限制条件的间接平差模型作为概括平差函数模型[1]具有列立误差方程式规律性强、参数平差值即为结果、便于编程计算等优点[2],但该模型中满秩的误差方程包含已知数据,约束方程也由已知数据建立,会混淆已知数据和观测数据2类不同性质的数据。若将平差系统中所有点作为未知参数,利用观测数据建立误差方程,用已知数据建立约束方程或基准方程,两者联合组成约束秩亏间接平差模型,不仅可有效区分观测数据和已知数据,并且在理解参考系效应和内部噪声、评定观测值的内部符合精度、分析已知数据对平差结果的影响[3-4]等方面具有明显优势。因此,约束秩亏间接平差模型被广泛应用于变形监测、近景摄影测量、GPS测量、地球参考框架建立[5-8]等大地测量数据处理中。
国内学者对解算约束秩亏间接平差模型的方法进行过大量研究[9-12],本文在这些研究基础上进一步分析约束秩亏间接平差模型的法方程系数四分块矩阵结构,研究其凯利逆矩阵的存在条件和显性表达式,并验证公式的正确性,为解算约束秩亏间接平差模型提供简单准确的方法。
1 特殊分块矩阵求逆
1.1 引理[13]
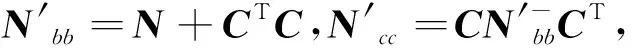
(1)
(2)
1.2 存在性条件
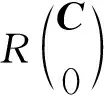
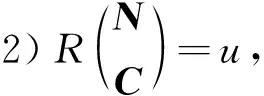
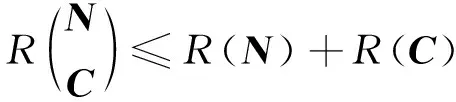
(3)
即
u≤r+s或u-r≤s
(4)
式(4)表明,C的行数大于等于N的秩亏数。
1.3 定理及证明
(5)
本文将通过广义逆矩阵法和矩阵变换法2种方法验证该表达式。
1.3.1 广义逆矩阵法
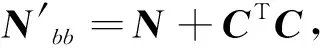
(6)
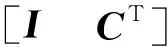
根据矩阵分解性质[15],存在u×u满秩矩阵A,使得行满秩矩阵:
(7)
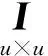
同理,存在u×u满秩矩阵B,使得列满秩矩阵:
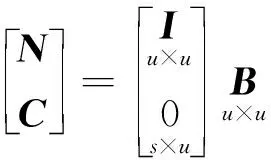
(8)
所以,

(9)

(10)
上述推算过程和结果表明,s×u行满秩矩阵和u×s列满秩矩阵相乘后可得s×s满秩矩阵。

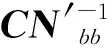
(11)
得证。
1.3.2 矩阵变换法
设
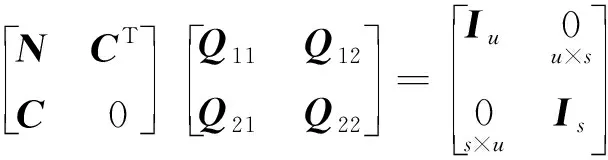
(12)
则:
NQ11+CTQ21=Iu
(13)
(14)
(15)
CQ12=Is
(16)
在式(15)左乘CT与式(13)相加可得:
(N+CTC)Q11+CTQ21=Iu
(17)
同理,将式(16)左乘CT再与式(14)相加可得:
(18)
联立式(15)~式(18),用矩阵形式可表示为:
(19)
(20)
可得:
(21)
得证。
2 约束秩亏间接平差模型参数的应用
2.1 约束秩亏间接平差模型的参数估计
约束秩亏间接平差模型可表示为:
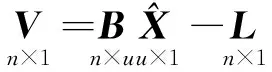
(22)
(23)
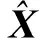
上述参数估计为约束条件下的极值求解问题,按照拉格朗日乘数法构造函数:
(24)
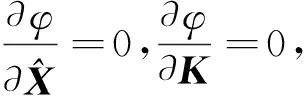
(25)
(26)
令N=BTPB,W=BTPL,用矩阵形式可表示为:
(27)
则:
(28)
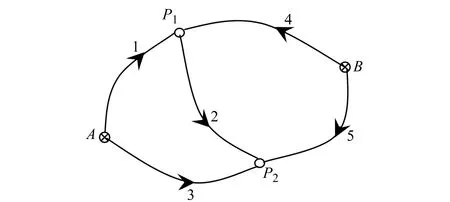
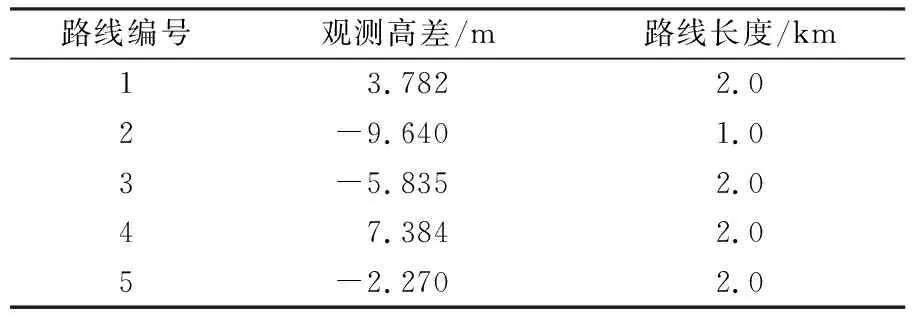
式中,N为u×u阶秩亏矩阵,R(N)=R(B)=t (29) 展开得: (N+CTC)-1CT[C(N+CTC)CT]-1 C(N+CTC)-1}BTPL+(N+CTC)-1CT [C(N+CTC)CT]-1WX (30) 式(30)即为约束秩亏间接平差模型参数估计的一般显性表达式。 在图1所示的水准网中,已知水准点A和B的高程分别为HA=237.483 m、HB=233.868 m,为求P1、P2点的高程,进行水准测量,表1为测量高差和水准路线。分别采用约束秩亏间接平差模型和间接平差模型解算待求点P1、P2的高程,并对结果进行比较。 图1 水准网Fig.1 Leveling network 表1 观测数据 2.2.1 约束秩亏间接平差模型解算 式中,未知参数的系数矩阵B为列秩亏,符号⟺表示等价的矩阵形式。 A、B为已知点,可以组成限制条件方程: 按观测距离定义观测值的权重,并令1 km的观测高差为单位权,则观测值的权阵为: P=diag[1/2.01/1.01/2.01/2.01/2.0] 通过分析可知,上述误差方程式系数矩阵B秩亏数为1,限制条件方程系数C为行满秩,条件方程个数为2,大于秩亏数,满足存在性条件。 将已知参数B、P、L、C、WX代入本文推导的约束秩亏间接平差模型参数估计公式(30),计算可得: 2.2.2 间接平差模型解算 同理,按观测距离定义观测值的权重。 根据最小二乘原则,将已知参数B、P、L代入,解算得: 1)本文对左上角子矩阵秩亏、右下角子矩阵为零的特殊四分块矩阵进行分析,在满足左下角子矩阵为行满秩及行数大于左上角子矩阵秩亏数的条件下,证明其存在凯利逆矩阵,该存在条件可为自由网附加条件法的平差提供理论依据。 2)在通常的四分块矩阵求广义逆矩阵和凯利逆矩阵公式的基础上,利用广义逆矩阵法和矩阵变换法推导该类特殊四分块矩阵凯利逆矩阵的显性表达式。该公式可用于解算约束秩亏间接平差模型的参数估计,为约束秩亏间接平差模型的解算提供简单准确的方法,具有理论和应用价值。2.2 数值算例
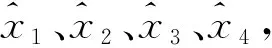

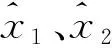
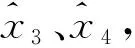
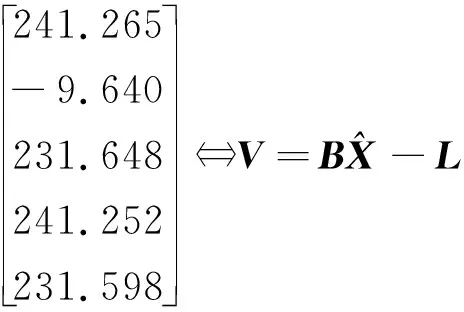
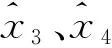
3 结 语
