偏载状态下轧机轴承接触力学模型研究

吝水林，孙建亮，彭 艳

(燕山大学国家冷轧板带装备及工艺工程技术研究中心，河北，秦皇岛 066004)

轧机滚动轴承是轧机装备的关键零部件，其性能和质量是保证轧机稳定运行的关键。轧辊轴承通常在高速高温的恶劣环境下工作，采用多列轴承来承受轧制负荷，辊身和辊颈由于轧制负荷过大发生弹性弯曲，径向载荷、轴向载荷和力矩载荷的联合作用导致各列滚动体和滚道单位接触长度上载荷非均匀分布。由于服役工况下轧机部件的磨损，现代轧制工艺的改进，轧制力、弯辊力、轴向力的联合作用，轴承的制造误差、轴承座的安装精度等综合影响，导致轴承在总负载不变的情况下各列滚动体承载不均，此外，推力载荷进一步加剧了滚动体与滚道接触应力的非均匀性，导致轴承长期在偏载状态下运行，大大降低了轴承的耐久性和疲劳寿命，严重影响轧机运行稳定性和生产效率。因此，有必要研究高速板带，轧机偏载状态下轧机轴承力学性能，对保证轧机稳定运行和提高轴承服役寿命有重要意义。

针对滚动轴承多种多样的应用领域及工况条件，研究者们从拟静/动力学模型[1−4]、动力学模型[5−7]、故障力学模型[8−15]、接触润滑理论及力学性能方面开展研究，力求构建轴承在复杂工况下运行的力学特性与服役状态，更好地服务于轴承设计与应用。

在拟静力学、拟动力学、动力学模型方面，Hertz[16]提出了空间点接触理论和平面无限长线接触理论，建立了接触问题的基本方程，该理论在轧机滚动轴承静力学分析上得到了广泛应用。Jones[17]在球轴承力学模型中考虑了钢球的离心力和陀螺力矩，并提出了套圈控制理论，通过Newton-Raphson 迭代法得到了滚动体的运动参数、载荷分布以及轴承刚度等重要参数。Rumbarger 和Filetti[18]将弹流润滑理论引入拟动力学模型中，建立了轴承动力学分析模型。张彪等[19]针对森基米尔轧机轴承提出了考虑轴承套圈变形的载荷计算分析方法，对于多辊轧机支承辊轴承等载荷计算，以Hertz 理论为基础的弹性变形理论难以满足，必须考虑套圈弯曲变形的影响。史修江和王黎钦[20]以D1842926 航空发动机主轴滚子轴承典型工况为算例，基于拟动力学分析结果，获得滚动体与套圈之间的接触微区运动和受力状态。陈芳华和汪久根[21]考虑接触体表面的弹性变形效应与润滑剂的压粘效应，建立圆锥滚子轴承的弹性流体动力润滑模型，并进行了完全数值解分析，得到了流体动压力分布、油膜形状与表面层内Mises 应力分布。

在求解轴承载荷分布结合有限元分析仿真方面，王思明等[22]在不考虑支撑结构刚度的情况下根据受力和变形的关系推导出变桨轴承沟道上载荷分布的计算公式，并计算出变桨轴承在某一负游隙时具有较好的力学性能。刘光明等[23]采用ANSYS/LS-DYNA 有限元软件，建立了包含支承辊轴承及轴承座组件、轧辊和轧件的四辊轧机三维实体同步耦合有限元分析模型，通过对比和分析咬入阶段、稳定轧制阶段和抛钢阶段各列滚动体的受力情况，得到了轧制过程中轴承载荷的分布规律。高学海等[24]不考虑轴承支撑结构和轴承套圈变形建立了双列四点接触转盘轴承的载荷分布与接触角分布模型，讨论了轴承几何参数对轴承承载能力的影响。聂重阳等[25]建立了线接触载荷作用下的界面力学分析模型。赵兴乾等[26]提出“径向轴承载荷增量”这一概念实现对整体隔振系统中轴系静态安全性定量分析，并计算了在不同螺旋桨推力载荷作用下及船舶纵倾工况下的轴承载荷增量。王兴东等[27]利用有限元分析软件建立低速重载轴承全模型，分析了轴承滚动体与沟道间的接触应力，轴承内、外圈的应力与应变，为分析轴承沟道疲劳寿命的应力计算奠定基础。Singh 等[28]使用显式动力学有限元软件包LS-DYNA，数值求解了带有外滚道缺陷的滚动轴承的动态非线性有限元模型。

在力学性能分析方面，曹宏瑞等[29]通过建立高速滚动轴承力学模型，基于外圈圆心位置不变假设，分析了滚动体受离心力、陀螺力矩、轴承内、外圈受热膨胀变形时，涉及轴承中滚珠变形状态和方位角的轴承时变刚度。Cavallaro 等[30]建立了高速柔性套圈圆柱滚子轴承的分析模型，研究了套圈的变形、轴承内部的受力分布、能量损耗以及滚子滑动速度与载荷分布的关系等。

上述研究从轴承的力学模型、力学性能、仿真分析等方面做了大量工作，但在轧机辊系运行过程中，未考虑配套轴承在恶劣的服役工况下以偏载状态运行时的动态行为和应力分布，本文针对机架辊系刚度偏差、来料楔形、非对称轧制工艺等因素引起的高速板带轧机辊系轴承的偏载力学行为，建立对应力学模型，研究了滚动轴承在高速偏载下的力学性能。

1 Hertz 理想接触模型

Hertz 接触理论是研究两物体因受压相触后产生的局部应力和应变分布规律的理论方法。对于滚子轴承，滚动体与内、外圈的接触可以看作是两曲面物体之间的相互挤压。Hertz 理论有如下假设：1)接触区发生小变形；2)接触面呈椭圆形；3)相接触的物体被看作是弹性半空间，接触面只有垂直分布压力。

1.1 弹性接触区和最大接触应力模型

图1 为弹性半空间内均布载荷分布，q 为作用在圆柱体半空间的均布载荷，R1和R2分别为两个圆柱体半径。由Hertz 线接触理论可知，在q 的作用下，两圆柱体的中心轴线相互趋近，在接触界面会产生宽度为2a 的接触区，如图2 所示，P0为均布载荷下的最大接触应力，a 为接触界面半宽度，实际运行中滚动体与内、外滚道接触时会分别产生上、下两个接触区，如图3 所示，最大接触应力P1和P2、接触半宽度a1与a2的计算如下。

图 1 弹性半空间均布载荷分布Fig. 1 Uniform loads distribution in elastic half space

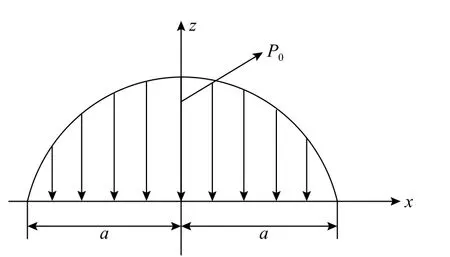
图 2 接触界面放大图Fig. 2 Enlarged contact interface

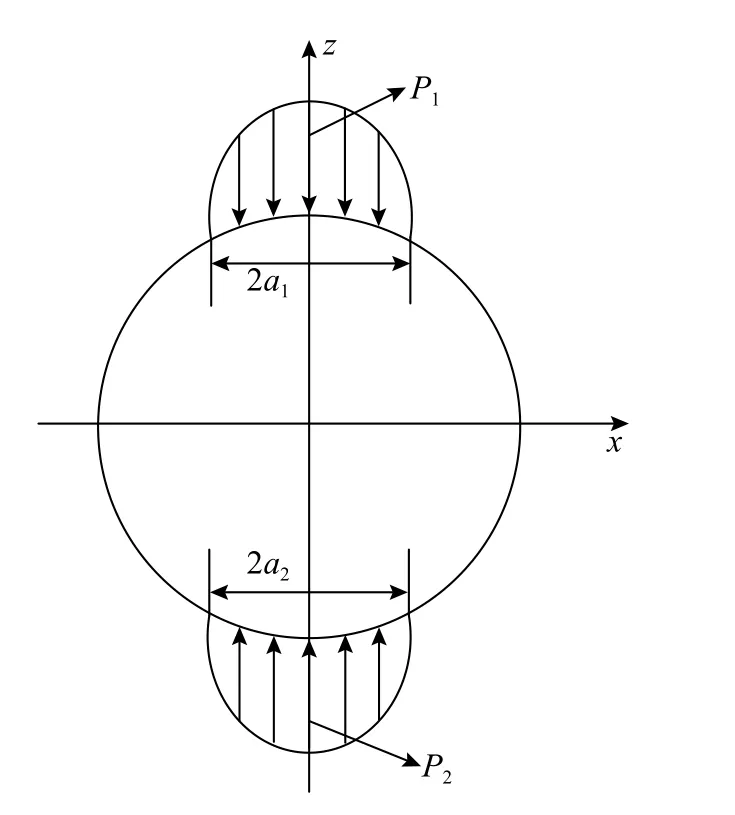
图 3 半椭圆接触示意图Fig. 3 Schematic of semi-elliptical contact

1.2 接触载荷与弹性趋近量关系

弹性趋近量即为滚动体与内、外圈接触时的弹性变形量，图3 中滚动体与内外圈接触时的弹性趋近量通过赫兹理论的基本方程无法求解，大多数情况下难以找到闭合形式的理论解，大多采用修正的Palmgren 经验公式，它考虑了滚子与滚道的直径以及曲率的凹凸性，如式(3)所示：

2 偏载接触效应的形成与建模

2.1 偏载接触效应的形成

图4 所示为轧制负荷大、来料楔形、非对称轧制、轴向力、轧机各部件磨损、轴承制造误差及非对称因素等导致轴承内、外圈产生角度为θ 的倾斜现象，滚动体在轴向方向应力不同，各列滚动体也由于轴颈的倾斜承受不同的轧制负荷，导致轴承长期处于偏载状态下运行。轴承承受径向载荷的传递路径为辊径到内圈，内圈到滚动体，滚动体到外圈，外圈到轴承座，本节主要研究在偏载状态下滚动体与滚道的接触效应。

图 4 轴承套圈的倾斜Fig. 4 Tilt of the bearing ring

2.2 偏载下有限长线接触模型及数值算法

图5 为偏载状态下采用条形单元法将载荷接触区进行离散化处理。四列圆柱滚子轴承的滚子与滚道接触长度有限，圆柱滚子与内、外圈的滚道发生倾斜形成偏载效应时，无限长圆柱体之间理想化接触状态不再适用，超出了赫兹线接触理论的范围，属于非赫兹接触问题。对于非赫兹接触问题，假设滚动体与滚道接触区在平行于轴承径向平面被划分为一定数量的条形单元，由于接触变形很小，可以忽略条形单元之间的切应力，仅仅考虑弹性变形。建立各个单元的力平衡方程和弹性变形方程，取滚动体与内圈的接触区进行分析。单元j 中，在x 轴上任一点上的接触应力为：

式中：aj为j 单元宽度；hj为单元长度的一半；Zi(yi)为第i 个单元的y 轴几何中心的表面函数值；Q 为总体载荷；E′为等效弹性模量；Dij为影响系数。式(9)构成 n+1线性方程组，当Q 和Zi已知时，可以解出Poj和 δ共n+1未知数。

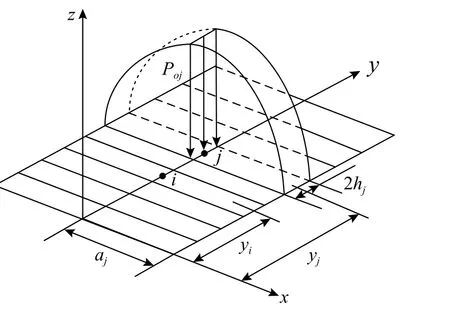
图 5 接触区条形单元Fig. 5 Bar units of contact area

影响系数Dij表示j 单元上的力对i 单元位移的影响，完善了传统切片法的各单元之间不相关的缺点，使每个单元之间具有了相关性。影响系数具体计算如下：

式中：yi、yj分别为i、j 单元的中心坐标；h 为每个单元长度的一半，h=l/2n。

式(11)的进一步计算必须采用数值积分的方法。此外，对于基本方程组，应满足应力非负的约束条件，即 Poj≥0 (j=1,2,3···)。

采用一维方法，将滚子离散为n 个单元，每个单元直接采用柔度矩阵法进行关联，将有线长接触的基本方程化为n+1 个方程组，方程组需迭代求解，首先对弹性趋近量δ 和接触半宽aj赋初值，计算影响系数Dij、最大接触应力Pi，若在迭代过程中，Poj为负值，说明该单元未发生接触，进行排除处理，再利用力平衡方程，对所有Poj求和，判断其是否满足平衡条件，即是否收敛。若不收敛，则调整δ，重新迭代，直至其收敛，图6为计算流程图，其中am是中间变量，储存上一次循环 aj的值，ε1、ε2为误差控制小量，调整δ 时，采用线性误差控制方案，此外aj的调整方案采用均值调整方案。

图 6 有限长数值解法计算流程Fig. 6 Calculation process of finite length numerical solution

2.3 滚动体与滚道接触模型及数值算法

图7 为单列轴承界面，可以清楚看到径向力及滚子位置角，径向载荷下，在位置角为φi的滚动体处，其与内、外圈接触的弹性变形量为：

由此，可确定Qri和αi，通过2.2 节圆柱滚子轴承的有限长数值解法，可求解位置角处滚动体的接触应力分布。图8 为单个滚子在力和力矩综合作用下平衡示意图，对于单个滚动体，求解力与力矩。

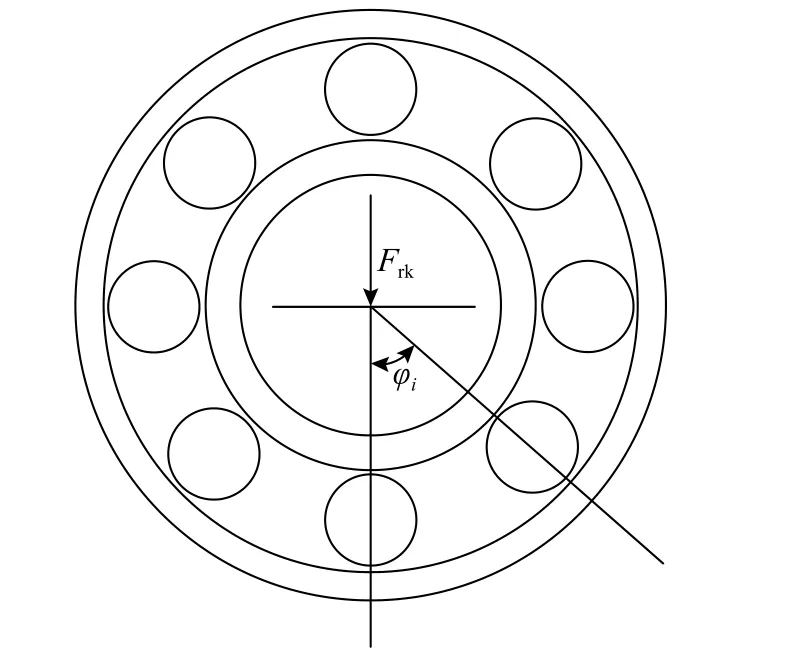
图 7 单列轴承截面Fig. 7 Cross section of single row bearing

图 8 力与力矩平衡Fig. 8 Force and moment balance

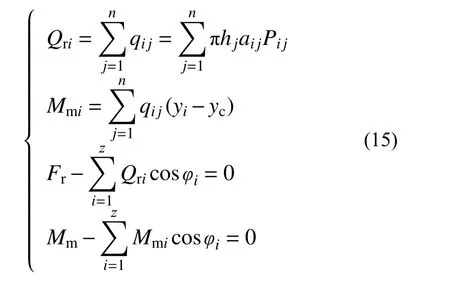
式中：n 为沿滚子长度划分的单元数；qij为单元上的集中载荷；hj为单元长度一半；aij为接触半宽度；Pij为每单元内的最大接触应力；Fr为径向载荷；yi为单元中心坐标；yc为滚动体中心坐标；z 为滚子个数，力学模型可通过迭代求解。

将上述模型编制计算机程序，如图9 所示，可计算总径向力与力矩、单个滚子的接触载荷、接触应力与弹性变形等，具体流程如下：首先给定轧辊和轴承的材料、尺寸参数及辊间载荷q，通过分析轧辊，确定轧辊作用与轴承的总径向载荷Fr和辊颈倾斜角θ。进入外循环对四列圆柱滚子轴承上每列轴承的等效径向载荷Frk赋初值，初值设定为总载荷的1/4。进入内循环对每列轴承的径向位移δrk赋初值，通过方程求解每个滚子的接触载荷并确定约束条件。之后代入2.2 节单个滚子有限长接触的数值计算程序中，求得单个滚子的接触应力Pij、接触半宽aij、宽度hj与集中力qij，利用数值计算的结构，计算单列滚子等效径向力和力矩，通过误差控制小量εr判断是否收敛，不收敛采用线性误差控制方案调整δrk，收敛稳定，循环迭代结束。

图 9 计算流程图Fig. 9 Calculation flowchart

3 理想及偏载接触模拟仿真

建立有限元分析模型时既要如实反映轴承实际结构的重要力学特性，又要采用较少单元数量以及简单的单元形态。本研究采用四列圆柱滚子轴承FC4666170，图10(a)为建立的三维有限元模型，在整体模型基础上提取内圈和滚动体接触模型，建立基于Hertz 理论的理想接触模型，图10(b)为整体网格划分，图10(c)为滚动体网格划分。

1)划分单元及确定接触类型。理想接触模型采用8 节点四面体单元，通过控制接触区域的网格密度来保证计算精度，采用手动划分网格的方法，单元数量25 988，节点数80 196。三维有限元模型整体采用8 节点四面体单元和8 节点六面体单元耦合形式，滚动体与滚道接触区域网格细分，滚动体等规则体采用8 节点六面体单元，非规则体采用8 节点四面体单元。单元数量176 933，节点数506 146。采用柔体-柔体的点-面接触类型定义内外滚道与滚动体之间的接触。

2)设置接触对、边界条件及外载荷。理想接触模型设置滚动体与内滚道的接触对。有限元模型设置四个接触对：滚动体与内、外滚道、轴承座与外圈、内圈与辊径。在理想接触模型四象限位置留硬点。在Mechanical 中设置2D Behavior 为平面应力类型，内圈与大地接触线添加固定约束，滚动体及接触区创建位移约束，X 方向为0，Y 方向自由。偏载接触模型中轴承座两个侧表面施加X 方向约束，轴承座前表面施加Z 方向约束，使其轴向固定，支承辊中间处设置对称约束。理想接触模型滚动体上施加径向载荷。偏载接触模型外载荷通过轴承座施加于轴承。

图 10 有限元分析模型Fig. 10 Finite element analysis model

4 算例与分析

4.1 计算参数

以生产线的850 mm 四辊冷轧机支承辊为例，采用配套的四列圆柱滚子轴承FC4666170，支承辊与轴承的模型参数如表1 所示，以实际工况为算例。

表 1 模型参数Table 1 Model parameters

4.2 结果计算与分析

4.2.1 理想接触模型结果对比

对理想接触模型模拟，取0°位置角滚动体与内圈接触模型，图11 为采用理想接触模型进行有限元计算的位移分布图与应力分布图。从图11 中可以看到接触区的半椭圆分布形式，与Hertz 接触理论假设相同，接触应力上、下对称分布，最大接触应力出现在接触区中线附近。本次分析只考虑表面及表面附近的应力所产生的变形以及由接触应力所产生的变形，由于滚动元件的刚度特性，本文采用的钢制轴承变形一般小于0.025 mm，由表2 可知，接触半宽度、最大接触应力、弹性趋近量等关键参数的误差控制在实际工程要求范围内，有限元解与解析解吻合程度较好。

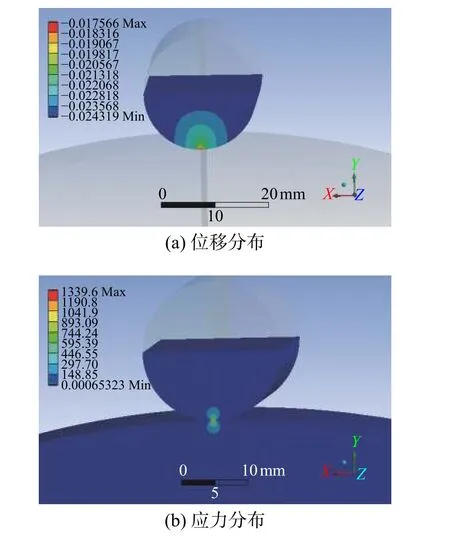
图 11 有限元结果分布云图Fig. 11 Cloud diagram of finite element results

4.2.2 径向力与弹性变形量

图12、图13 为每个滚动体的总径向载荷和弹性变形量，总轧制力在操作侧轴承和传动侧轴承两侧对称分布，轴承第1 列～第4 列的顺序为靠近辊颈侧到远离辊颈侧。辊间倾斜角为0.01°，通过计算可知轴承各列的总径向力Fr分别为246.15 kN、232.05 kN、217.95 kN、203.85 kN，总力矩Mm分别为46.51 N·m、46.08 N·m、45.63 N·m、45.16 N·m。整体结构呈对称分布，取右侧滚动体分析，最上端滚动体为0°位置角，滚动体所在位置角分别为0°～180°。同一列滚动体，随着其所在位置角的增大，径向载荷和弹性变形量逐渐减小，90°变为0°，滚动体与滚道开始脱离接触，不再有接触应力和接触变形。相同位置角的不同列滚动体，承受径向载荷和变形量依次减小。

表 2 数值解析解与有限元解对比Table 2 Comparison of numerical analytical results withfinite element results

图 12 单个滚子的总径向载荷Fig. 12 Total radial load of single roller

图 13 单个滚子的弹性变形量Fig. 13 Amount of elastic deformation of single roller

4.2.3 滚动体接触应力

图14 为单个滚动体沿长度方向的接触应力分布，对于每一个滚动体，单元接触应力沿滚子长度依次减小，接触应力分布呈“半船形”，最大接触应力达到1500 MPa 左右，且第1 列～第4 列最大接触应力依次减小，也间接反映了列间偏载的状态，滚动体的边缘接触应力比中心位置大，本模型考虑了滚动体端部发生应力集中现象，弥补了Harris 的简单切片法不能反映滚动体端部应力集中的弊端。

4.2.4 偏载接触模型结果对比

图15(a)为有限元模拟的单列滚动体周向最大接触应力，图15(b)为利用迭代进行数值求解的周向最大接触应力结果。滚动体端面与内滚道产生接触变形，最大接触应力随着滚动体位置角急剧变化，为了使分析过程更具有一般性，三维模型中滚动体在周向方向装配是随机的，模拟中0°位置恰好没有滚动体与套圈接触，15°～30°位置角的滚动体，承载力最大，整体呈“M”形分布，超过90°后，接触应力急剧降为零，滚动体与套圈没有发生有效的接触，即没有起到承载作用。图15(b)的数值计算结果中设置同样边界条件，结果显示在0°位置角附近没有数值显示，说明在15°～30°处应力数值已达到顶峰，与有限元分析中在0°位置急剧降为零趋势相同。有限元分析结果中第1 列和第2 列接触应力大于第 3 列和第4 列，整体趋势与数值求解结果相同，整个偏载过程可以很清晰看到。由于有限元分析更接近实际模型和工况，计算结果更精确，且略小于数值求解结果。

图 15 滚动体周向最大接触应力分布Fig. 15 Maximum contact stress distribution on the roller in the circumferential direction

4.2.5 不同载荷分布对偏载接触效应的影响

以上介绍了在均布载荷q=2×106N 时轴承整体及单个滚子的受力及变形情况，以下将讨论不同载荷分布的影响。图16 为每列轴承在不同分布载荷下承受的总径向力，随着工况载荷的增大，同一列的总径向力在不断增大，四列径向力线性分布的斜率增大，随着均布载荷的增加，轴承上各列载荷的偏载程度越来越严重，致使轧制轴承长期处于严重偏载的状态运行，大大降低了使用寿命。

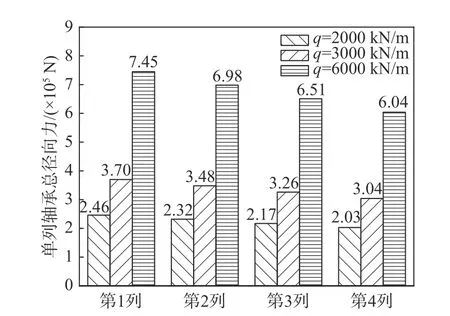
图 16 不同载荷分布时单列轴承径向力对比Fig. 16 Radial force comparison of single-row bearings under different load distributions

5 结论

本文针对机架辊系刚度偏差、来料楔形、非对称轧制工艺等因素引起的高速板带轧机辊系轴承的偏载力学行为，建立对应力学模型，研究了滚动轴承在高速偏载下的力学性能。针对辊间不同载荷进行了模型数值求解，仿真模拟了理想及偏载接触过程。研究为延长轴承使用寿命、保证轧机安全稳定运行提供理论依据，具有重要工程意义。主要结论包括：

(1)模拟了Hertz 线接触问题。对理想接触模型模拟，取0°位置角滚动体与内圈接触模型，通过有限元计算的位移分布图与应力分布图得到接触区的半椭圆分布形式，接触应力上、下对称分布，最大接触应力出现在接触区中线附近，解析解与有限元解误差在15%以内。

(2)同一列滚动体，随着其所在位置角的增大，径向载荷和弹性变形量逐渐减小，90°变为0°，滚动体与滚道开始脱离接触，不再有接触应力和接触变形。相同位置角的不同列滚动体，承受径向载荷和变形量依次减小。

(3)滚动体在周向随机装配，在15°～30°位置角的滚动体，承载力最大，整体呈“M”形分布，超过90°后，接触应力急剧降为零，滚动体与套圈没有发生有效的接触，没有起到承载作用。

(4)对比了不同载荷分布对偏载接触效应的影响，随着轧制载荷的增大，轴承同一列滚子的总径向力不断增大，并且四列径向力线性分布的斜率增大，随着轧制载荷的增加，轴承各列载荷的偏置程度越来越严重。