一种多自由度阻尼体系动力问题的高阶分析方法

李鸿晶，杨筱朋，梅雨辰

(南京工业大学工程力学研究所，南京 211816)

结构动力响应分析是认识动态系统性态和行为的基础性工作。传统的动力响应分析方法可以大致分为两种类型：一类是基于坐标变换[1−2]的方法，如振型叠加法、频域法等，一般适用于线弹性体系和经典阻尼体系的动力问题；另一类为直接积分法[3−6]，其直接对体系运动微分方程进行求解，以Newmark-β 法等逐步积分法为代表，可以解决非线性体系和非经典阻尼体系的动力分析问题。这些传统动力分析方法中有些算法具备无条件稳定及可控算法阻尼等特性[7]，多采用低阶格式，精度一般不超过二阶。也有一些算法采用了高阶格式，精度能达到三阶以上，但所需的计算量及存储量要增大不少[8]。有别于传统动力方法，精细积分法(precise time-step integration method,PTIM)[9−18]则利用体系动力响应积分解，通过计算矩阵指数获得动力响应。由于结构大型化、复杂化以及精细化分析等方面的需要，发展高效率的动力分析方法始终是一种非常现实的需求。

微分求积 (differential quadrature, DQ)法[19−22]是近年发展起来的一种求解微分方程(组)的数值方法，Fung[23−25]首先将其应用于初值问题，其后一些学者也开展了相关研究[26−32]，逐渐形成了动力DQ 分析方法。该方法数值稳定性好，计算简便且精度高，然而由于其以位移响应为基本未知量来离散动力方程，所得数值格式为隐式格式，因而需要求解方程。另外，目前已提出的这类动力方法因稳定性和精度方面的要求多采用不等步距的时间离散方案，求解均匀布置的采样时刻处的响应值时需要进行插值，对其计算效率造成了一定的限制。与传统动力响应DQ 分析方法不同，在文献[33 − 34]中，以单自由度体系为对象提出了一种计算Duhamel 积分的高精度算法，即积分求微方法(integral differentiation method, IDM)。该算法为高阶方法，动力响应计算仅需要完成一次方阵与向量的乘法运算，一次计算即可同时获得多个时刻的响应值。整个过程无需求解方程，且可采用等时间步距的计算方案，不必通过插值即可直接获得各等距分布时点的响应。积分求微法可视为非齐次动力方程的一种数值解法，如果将其向多自由度体系推广，则将引入矩阵指数。由于积分求微法无需进行数值积分计算，与单自由度体系动力响应分析过程相比较，多自由度体系动力分析仅需要处理矩阵指数的计算。

本文将逆用DQ 原理，建立多自由度阻尼体系动力时程分析的积分求微算法，以丰富动力响应分析的技术手段。

1 多自由度体系状态响应

动态荷载向量p(t)激励下的多自由度阻尼体系运动方程写为：

状态方程式(3)中的系数矩阵H 仅包含体系刚度、质量和阻尼的特性，因而它是反映体系动态特性的。对于线弹性体系动力分析，体系特性矩阵H 将是时不变的常数矩阵。而方程的非齐次项中含有荷载向量p(t)，它描述了环境对体系施加的动态作用的特性。

式(3)的解可采用 Duhamel 积分的形式表示为：

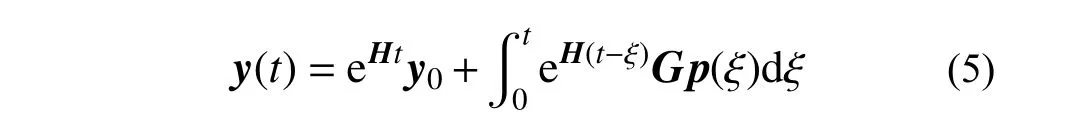
式中， eHt为矩阵指数。

形如式(5)的方程解中包含了矩阵指数及其积分式，对于实际动力问题，试图利用式(5)获得体系动力响应y(t)的解析解答几乎是不可能的，但可以通过数值方法得到y(t)的近似结果。

2 动力响应积分求微分析

利用式(5)计算y(t)的难点在于含有矩阵指数项的卷积的计算。将该卷积做如下的分离：

显见，求得动力响应y(t)的关键是处理好两个问题：一是矩阵指数T(t)的计算；二是计算出变上限定积分函数向量D(t)。两者都要求建立起适合的数值算法。

考虑动力持时中的任意时段[ti, tj]，该时段包含有ρ 个时步，其中ti、tj均选择位于采样点处。如图1 所示，假定采取等距采样，采样周期为δ，则时段[ti, tj]的长度应为：

图 1 动态响应待求解时段Fig. 1 The solved time interval for dynamic response

2.1 矩阵指数Tk 的计算

根据矩阵指数的Taylor 级数定义，矩阵指数Tk可表示为：

2.2 定积分 Dk 的计算

由式(8)可见，D(t)对时间t 的导数可表示为：

观察上述求解动力响应的过程，可以发现除了在确定系统特性矩阵H 时需要对质量矩阵m 求逆，以及在确定转换矩阵B 时需要对Vandermonde矩阵进行求逆计算外，其余过程都不需要矩阵求逆或者求解线性方程组。而对于结构体系可采用集中质量模型，即质量矩阵m 为对角阵，其逆矩阵可以方便地求出。至于Vandermonde 矩阵求逆计算，可以事先算出逆矩阵结果，考虑到实际动力分析时待求解时段 [0, ∆tij]内包含的时步数ρ 不可能很大 (一般取 ρ=10～15)，故可将转换矩阵B 制成表格，动力响应分析时直接取用即可。鉴于此，按照式(32)计算积分矩阵Φ 时仅需做矩阵乘法运算，这相当于是一种显式算法。

3 算法步骤

依据上述推导，可将多自由度阻尼体系动力时程积分求微法总结为下述算法：

4 数值稳定性分析

对于线性体系动力方法的数值稳定性，只需研究如下的单自由度体系方程：

阻尼一般对稳定性起到有利作用，因此研究稳定性时多不考虑阻尼的影响。以下分析都是在消除阻尼项后开展的。观察式(12)的动力响应数值格式，可得时段初始点与末点的递推关系式：

表 1 L 不同取值时的稳定极限值Table 1 The limit of stability with different L

由此可得出，本文方法一般为有条件稳定方法，当L=3、4、7、8 时，稳定极限较大，稳定性相对较好，再综合考虑计算量的因素，取L=4 比较合适。由于在精细积分法中λ 一般选20，即时步小段的长度 η ≈ 9.54×10−7δ，因而只需要各节点间距满足：

即可稳定地进行计算。显然，通常情况下该稳定极限条件是极易得到满足的，当取L=4 时本文方法时步大小的取值几乎不受稳定性的限制。

5 算例分析

通过两个算例阐释本文方法的特性，第一个算例用来验证本文方法的可靠性，包括收敛性和精度；第二个算例重点阐释本文方法的适用性。

5.1 两自由度体系算例

选择文献[12]中的两自由度体系算例，其特性矩阵分别为：

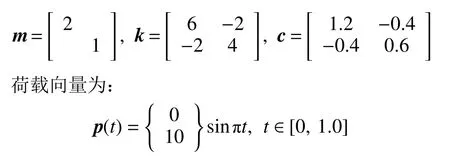
采用本文的IDM 法计算该体系的位移响应和速度响应，并以精确解为标准验证计算结果。为了清晰地展现本文方法的收敛性及精确性，将时段内时步数ρ 取为10，时段长度Δt 从1.0 s 开始依次减为原来的1/2 时，即分别取Δt=1 s、1/2 s、1/22s、1/23s 时，计算体系在 t=0.2 s、0.4 s、0.6 s、0.8 s、1.0 s 处的响应值。计算结果同精确解的最大绝对误差Err 与Δt 的关系曲线如图2 和图3 所示，其中横坐标和纵坐标皆采用以2 为底的对数坐标。

观察图2 和图3 可以发现，随着时段长度Δt 的减小，本文方法计算结果的误差亦迅速减小。当Δt 缩小到1/23s 时，无论是位移响应还是速度响应，其最大绝对误差皆不超过10−14数量级，计算结果已非常精确，具备较完美的收敛效果。从整个时步的取值过程来看，本文IDM 法的收敛速度非常快，几乎是时步长度每缩小一倍计算结果的绝对误差就会减小约2−10量级。进一步观察可以直观地发现在对数坐标系下最大绝对误差与时步长度近似呈线性关系，这符合数值计算原理中误差与时步长度的关系：

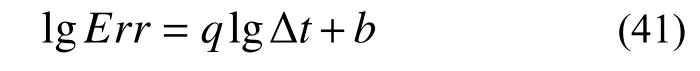
式中：绝对误差Err 对于函数可以用其范数来近似替代；q 为数值格式的收敛精度阶数。

图 2 不同Δt 下体系位移响应最大绝对误差Fig. 2 The maximum absolute error of the displacement response of the system with different Δt

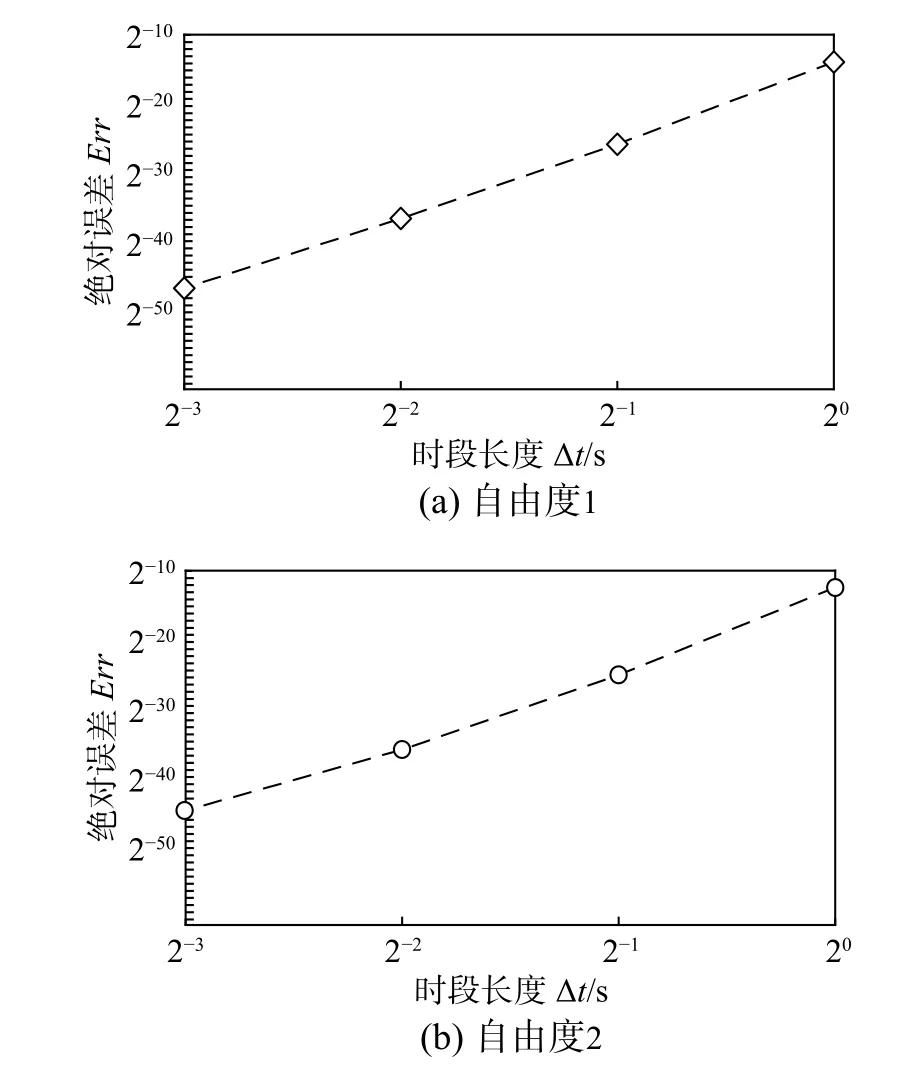
图 3 不同Δt 下体系速度响应最大绝对误差Fig. 3 The maximum absolute error of the velocity response of the system with different Δt

为合理有效地估计本文IDM 方法的收敛阶数，分别选取整体误差指标——最大绝对误差以及某个时刻(如t=0.4 s)时的局部绝对误差两个指标作为式(41)中的误差项Err，采用最小二乘法估算出体系位移响应和速度响应的收敛阶数q，结果列于表2 和表3。

表 2 响应收敛阶数q 估计(整体误差指标)Table 2 Evaluation of convergence order q for responses based on whole error criterion

表 3 响应收敛阶数q 估计(局部误差指标)Table 3 Evaluation of convergence order q for responses based on local error criterion

由表2 和表3 的统计结果，无论是采用整体误差指标还是局部误差指标，各质点的位移响应和速度响应的收敛阶数皆在10～11，即该数值格式对于位移响应和速度响应的收敛精度至少为10 阶。而加速度响应是依据位移响应和速度响应由运动方程求得的，因而其具备与位移响应、速度响应相同的收敛精度。另一方面，从理论上来看，本文IDM 数值格式的收敛精度主要由矩阵指数的计算精度和DQ 法的逼近精度所共同决定。而矩阵指数的计算由精细积分实现，其数值逼近的时间节点间距非常小，计算精度相较于非齐次项DQ 逼近要高许多。因此可以认为，本文IDM法的收敛精度主要由DQ 法的计算精度决定，它直接取决于时段内的时步数ρ 的取值。由DQ 原理可知，在各时段Δt 内对其积分函数D(τ)逼近的绝对误差函数为：

从式(42)来看，其误差函数是Δt 的ρ+1 阶无穷小，即本文格式具有ρ+1 阶代数精度。当取ρ=10 时，本文方法收敛精度阶数的理论值为11。考虑到计算机舍入误差及矩阵指数的影响，实际计算时收敛精度会略微小于理论值。即实际计算时若取ρ=10，本文方法至少能达到10 阶收敛精度，这同表2 和表3 中估计的结果相符合。一般地，当计算时段内包含的时步数为ρ 时，理论上本文方法有ρ+1 阶代数精度，实际计算时至少能达到ρ 阶精度。

下面将本文IDM 法与传统动力方法进行比较，选择的传统方法包括Newmark 常平均加速度法 (取 γ=0.5、β=0.25)、Wilson-θ 法 (取 θ=1.4)和精细积分法(PTIM)。将所有这些方法的计算结果列于表4，同时给出了精确解作为比较的标准。

表 4 不同动力方法计算的位移响应结果Table 4 Computational results of displacement response by different dynamic methods

续表 4

观察表4 可以发现，当时段长度取为Δt=1.0 s时，划分10 个时步，本文积分求微法的计算结果与精确解已非常接近，最大相对误差在2%以内。

注意到本文IDM 法为高阶方法，此时待求解时段[ti, tj]内含有的10 个时步的步距均为δ=0.1 s，而传统的 Newmark-β 法和 Wilson-θ 法在步距取为0.05 s 时位移响应的最大相对误差已超过了10%，在取为0.02 s 时，也超过了2%。也就是说，在步距是这两种传统逐步积分方法5 倍的条件下，本文IDM 法的计算结果仍然比其要精确些，这直观显示了本文方法高精度的特点。

5.2 弹簧-质量体系算例

以图4 所示的串联弹簧质量体系为例，取自由度数N=100。为了使体系固有频率覆盖范围广，弹簧刚度一半设置为较刚，另一半设置相对较柔，其特性参数见表5。每个质点都受到相同的水平简谐荷载激励：

图 4 100 自由度弹簧质量体系Fig. 4 Schematic plot of 100-degree of freedom spring-mass system

表 5 弹簧-质量体系的基本特性Table 5 Properties of the spring-mass system

该100 自由度体系的基本频率为0.98 rad/s，最高阶频率为1094.92 rad/s，从低频覆盖到极高频，便于全面地考察本文方法的数值稳定性。取截断项数L=4、时段分段数ρ=10，采用本文IDM法计算体系每隔0.01 s 的动力响应。选用不同的时段长度Δt，计算结果与显式中心差分法(取Δt=0.001 s)进行比较。图5 和图6 分别为最右端质点(DOF 100)和第50 个质点(DOF 50)的位移时程曲线。这里需要说明的是，对于该体系中心差分法的稳定极限为Δt≤0.0018 s，因而采用Δt=0.001 s可得到稳定的计算结果，且它是直接获得0.01 s 时间间隔响应所允许的最大步距。

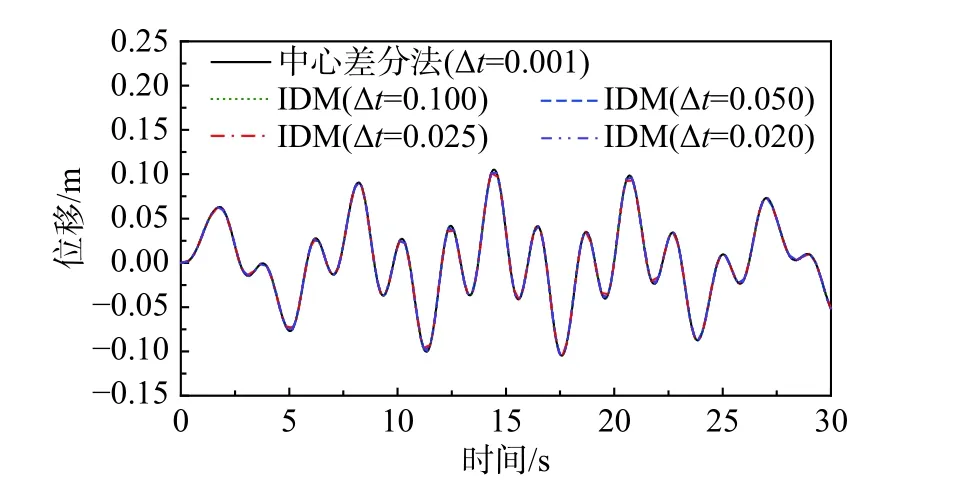
图 5 体系第100 自由度位移响应对比Fig. 5 Comparison of the displacement responses of the DOF 100 in this system

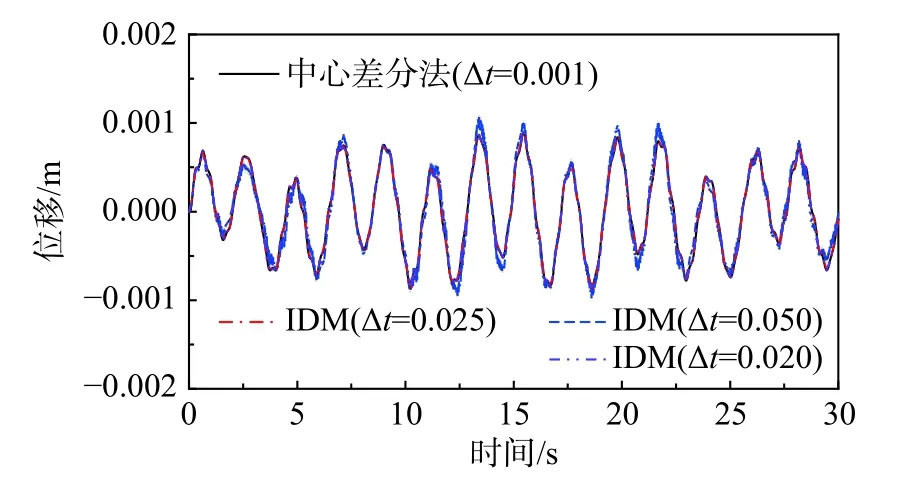
图 6 体系第50 自由度位移响应对比Fig. 6 Comparison of the displacement responses of the DOF 50 in this system

观察图5 和图6 的动力响应计算结果，IDM法在选择大得多的步距情形下依然能够获得稳定的计算结果。例如，将时步长度放大至0.1 s 时，利用IDM 法计算最右端质点的位移响应，仍然没有任何失稳放大现象产生。此情形下其时段长度已是中心差分法稳定极限的50 倍以上，在较高自振频率的参与下依然能得到稳定可靠的结果，这充分显示了本文方法良好的数值稳定性。

下面进一步考察本文IDM 法的计算效率。为了更直观地体现算法的执行效率，表6 给出了一些情况下IDM 法与中心差分法(CDM)耗费的计算时间及两种方法计算时间的比值。其中所有的计算皆是在同一台计算机上完成的，该计算机的架构为英特尔Xeon(R)W3565 中央处理器，主频3.20 GHz。各类情况的计算时间均用符号CPU 来表示，且该时间是纯计算时间，不包括数据输出及单位换算的时间。

表 6 不同方法CPU 时间对比Table 6 Comparison of CPU time with different methods

观察表6，对于IDM 法，当时段长度取为0.05 s 时其计算时间还不到中心差分法的40%，当时步缩小到0.025 s 时也只有CDM 法的70%左右。通过对比各响应时程计算结果，可以发现对于DOF 100 质点的位移响应，IDM (Δt=0.05 s)和IDM (Δt=0.025 s)的计算结果与CDM 的结果基本一致，而对于DOF 50 质点，IDM (Δt=0.025 s)的计算结果与中心差分法基本一致，而IDM (Δt=0.05 s)的精度稍差一点。但即便如此，在IDM 法与CDM法精度大致接近的情况下，其计算时间依然比中心差分法要少30%左右，从而在时间复杂度上IDM 法要低于传统的显式中心差分法。另外，IDM(Δt=0.025 s)在整个持时内的时间采样点数量仅为CDM(Δt=0.001 s)的 40%，虽然 IDM 法结构特性矩阵的元素数量是中心差分法的4 倍，但对于线性时不变体系而言仅需存储一次，且有近1/2 是零元素。相较于中心差分法，IDM 法凭借更少的时间采样点数，随着荷载持时的延长其空间复杂度的优势必将愈加明显。综上所述，本文IDM 法在计算复杂度(包括时间复杂度和空间复杂度)上要低于传统的显式CDM 法，由于CDM 已是目前效率较高的动力分析方法，表明本文IDM 法在计算效率方面具有一定优势。

6 讨论与结论

根据DQ 原理，函数在指定点处的导数值可以用域内一系列离散点处函数值的加权和来近似表示。将DQ 原理用于偏微分方程求解时，传统上都是将域内离散点处的函数值视为待求解的未知量，然后利用DQ 原理将各离散点处的导数值分别以函数值线性加权和替代并代入微分方程，从而将微分方程转化为代数方程组，进而获得微分方程的近似解答。由于DQ 法高精度、低计算消耗的特点，这种基于DQ 原理的微分方程数值解法仅需付出不大的计算工作量即可获得较高精度的数值解。对于时间相关问题，传统的基于DQ原理的动力响应分析方法都是沿用了这种求解思路，即将各离散时刻的速度响应和加速度响应分别表示为时段(步)内全部离散时刻位移响应的加权和。但是像动力响应Duhamel 积分解这样的在被积函数中含有指数函数乘积项的定积分式，在积分变量分离后其导数即为被积函数自身，所以这种类型卷积的导数是非常容易求得的。同传统的DQ 法应用不同，本文的积分求微法中离散点处的导数值是在应用DQ 原理前就已经求得的，这样只需通过权系数逆矩阵进行变换即可求得位移响应向量，即动力响应计算仅需执行矩阵乘法运算即可一次性地求出时段内的全部位移响应值。而权系数矩阵的求逆计算只涉及Vandermonde矩阵求逆，这可以事先求出并在程序中存储。因此，本文的动力响应积分求微方法相当于显式方法，其关键在于对DQ 原理的逆用。

经过逆用DQ 原理后，动力响应分析只需解决矩阵指数计算即可完成。PTIM 是实现矩阵指数计算的一种优秀算法，具体应用到本文动力响应积分求微方法中，需要注意几个问题：

首先，本文动力响应积分求微法是按照时段进行求解的，每个待求时段内都包含有若干个时步。根据矩阵指数加法定理，在等距时步采样即待求时段内各时步的步距相同的前提下(事实上动力分析一般都会采取这种等时步方案)，各个时步端点的响应值才能表示成像式(19)那样的矩阵指数递推格式。这样，当采取等距时步方案时只需要计算出待求时段内第一个时步对应的矩阵指数，然后通过递推公式就可以计算出时段内所有时步的矩阵指数。显然，矩阵指数精细积分计算仅仅被限制在第一个时步，即整个时段动力响应分析只要求一次精细积分计算，而不必采用PTIM计算多个矩阵指数。这是实施本文动力响应积分求微法的一个要点。也就是说，在本文积分求微动力分析方法中应用PTIM 计算矩阵指数可以获得较高的计算效率，关键在于动力时程等距分布的采样点同时也被选择为DQ 离散节点，这样就只需要在第一个时步内应用PTIM，即在每个求解时段内只需使用一次PTIM 完成矩阵指数计算即可。

但是，使用DQ 法时一般会选择不等距节点离散方案，采取等距节点方案会降低DQ 分析的精度。如果采取不等距时步方案，则势必要求多次执行矩阵指数的精细积分计算，而且还需要进行插值才能获得动力分析结果，这将极大地增加计算工作量。所以，具体进行动力分析时就需要权衡计算的精度和效率。本文建议采取等时步方案，不仅因为这是动力分析的通常选择，而且可以将计算工作量控制在最低范围。由于DQ 法的高精度属性，即便采取等时步方案时也会取得相当高的计算精度。这从本文给出的算例中可以看出。

其次，由于PTIM 计算矩阵指数时分为2 个步骤，需要计算经过细分的很小步长内的矩阵指数，即首先需要计算出矩阵指数 eHη，然后才能通过递推得到需要求得的矩阵指数 eHδ(δ 为时步的步距，本文方法中只要求对 eHδ进行精细积分计算)。在计算 eHη时，本文引入了秦九韶算法，将幂函数求和(被截断的Taylor 级数)计算转化为递推格式，每一步递推计算都只做一次矩阵乘法运算，有效地降低了计算工作量和数据存储空间。截断阶数L 越高，采用秦九韶算法的收益就会越大。

最后，由于本文方法逆用DQ 原理，所以不要求进行数值积分计算，但需要计算矩阵指数e−Hδ。在使用精细积分法时，矩阵指数 e−Hδ的计算可以连同 eHδ一起计算出来。只要将细分后的矩阵指数 eHη的被截断级数表达式中的奇数项和偶数项分列为2 组，然后分别使用秦九韶算法进行计算，最后通过两组结果相加得到 eHη，相减得到e−Hη。这样算法可同时计算出矩阵指数 eHη和e−Hη，而没有增加额外的计算工作量。其后递推计算 e−Hδ的过程与 eHδ完全一致，可以方便地计算出来。

另外，在文献[33]中针对单自由度体系实施积分求微分析时，待求时段内各时刻的响应值构成一个向量，因而可以只通过执行一次矩阵与向量的乘法运算就能计算出时段内的全部响应。而多自由度体系有所不同，因为待求时段内每个时刻的响应都是一个向量，故时段内所有时刻的响应实际上构成了一个矩阵，所以时段内全部响应需要通过矩阵与矩阵的乘法运算才能实现。

关于本文积分求微法的稳定性问题，在文献[33]中我们已经证明其为无条件稳定算法。但是对于多自由度体系，由于采用了PTIM 计算矩阵指数，所以该算法的稳定性不仅取决于积分求微计算即逆用DQ 原理本身，还与PTIM 的稳定性有关。关于PTIM 稳定性问题已有相关研究[35]，结论为PTIM 是有条件稳定算法，但稳定性条件极易满足，对于常规工程结构几乎不会出现失稳问题。事实上，本文之所以只计算第一个时步的矩阵指数，待求时段内的其他时步的矩阵指数都是通过递推的方式获得，也从另一方面说明了PTIM 具有非常好的稳定性。

综上所述，执行本文积分求微法的主要环节在于DQ 原理逆用和矩阵指数计算。通过引入矩阵指数及相应算法，本文将结构动力时程分析的积分求微法推广至多自由度情形，通过理论分析和数值试验，可得到如下结论：

(1) 结构动力时程分析的积分求微方法能够适用于多自由度体系的直接积分，计算结构动力响应是精确收敛的。该方法是一种高阶时程分析方法，包含ρ 个时步的积分求微法理论上具有(ρ+1)阶代数精度，与传统的低阶逐步积分方法相比有较高的计算精度。

(2) 本文的积分求微法一般是有条件稳定算法，其稳定性与截断项数L 有关。当L=4 时，稳定极限条件极易得到满足，在较大的步距和较高的体系自振频率参与下依然能得到稳定的计算结果，因而具备较好的数值稳定性。

(3) 本文方法可视为显式方法，无需进行方程求解，动力响应分析表现为矩阵与向量的乘法运算，一次计算能得到多个时刻的响应值，且无需对计算结果进行插值，因而计算效率较高，计算工作量要少于传统的显式中心差分法。

(4) 建立本文方法的关键环节在于对DQ 原理的逆用，对于多自由度阻尼体系动力响应分析，计算动力方程非齐次项时不再要求对定积分式进行特殊处理，从而可以直接应用精细积分法计算矩阵指数，有利于充分发挥精细积分法的优势。

(5) 本文方法属于高阶方法，在一个相对较长的时段内再划分出多个时步，然后同时求解。这种模式为进一步发展动力响应分析并行算法提供了有利条件。