基于改进Ibarra-Medina-Krawinkler 材料模型的RC 圆柱恢复力模型参数识别

代旷宇，于晓辉，王 硕，吕大刚

(1. 中国地震局工程力学研究所，中国地震局地震工程与工程振动重点实验室，哈尔滨 150090；2. 哈尔滨工业大学土木工程学院，哈尔滨 150090)

建立具有较高精度和效率的结构有限元模型对进行合理和快速的结构抗震性能评估意义重大。在结构有限元建模过程中，不同类型的恢复力模型被广泛用于描述材料、截面、构件和结构整体等多个尺度的非线性性能。相比于材料层次的结构建模方式[1−2]，利用构件的恢复力模型，建立结构的宏单元模型[3]可以大大简化结构模型的复杂性，提高数值模拟的精度和效率。

要建立较为准确的构件恢复力模型，需要对已有结构构件试验数据进行深入发掘。近年来，国内外学者基于不同类型构件的试验数据库，开展了一系列结构构件恢复力模型参数的识别工作。例如：Haselton 等[4]以美国太平洋地震工程研究中心(PEER)结构性能数据库(Structural Performance Database)[5]中的255 根弯曲破坏及弯剪破坏的RC方柱的试验数据为基础，进行了RC 方柱恢复力模型参数的识别，并给出了恢复力模型参数的经验预测公式。Lignos[6]搜集了超过600 根钢结构构件及RC 构件的试验数据并基于改进Ibarra-Medina-Krawinkler(改进I-M-K)材料模型对试验构件的恢复力模型参数进行校准，最后给出了构件恢复力模型参数预测公式。吕大刚等[7]将可考虑捏缩的改进Bouc-Wen 材料模型结合遗传算法对RC 梁-柱节点的恢复力模型进行了参数识别，并选用了11 个RC 梁-柱节点试验验证了所识别恢复力模型的准确性。此外，李长晋[8]采用Bouc-Wen 模型及微分进化算法，对锈蚀RC 柱非对称模型参数进行了识别。Sengupta 和 Li[9]基于修正的Bouc-Wen 模型，采用遗传算法对钢筋RC 梁柱节点滞回参数进行了识别。Lee 和Han[10]采用可以考虑捏缩效应的Pinching4 材料模型对40 根弯剪破坏及剪切破坏柱构件进行了参数识别。Dai 等[11]搜集了103根拟静力循环加载的锈蚀RC 方柱试件，采用改进I-M-K 材料对试件进行了参数识别，给出了锈蚀RC 柱的滞回模型。

根据已有相关研究，RC 方柱的恢复力模型参数识别工作已经得到了研究人员的广泛关注。然而，对于建筑和桥梁结构中广泛应用的RC 圆柱的恢复力模型参数识别工作，还未得到研究人员的充分重视。RC 圆柱与RC 方柱彼此之间在设计参数和构造措施方面均存在明显的差异，因此，已获得的RC 方柱的恢复力模型并不适用于RC 圆柱[4]。此外，研究人员已经积累了较多关于RC 圆柱的抗震性能的相关试验数据，这也给RC 圆柱的恢复力模型参数识别提供了坚实的数据基础。

鉴于上述，本文选取PEER 结构性能数据库中76 个RC 圆柱试验数据作为研究对象，采用峰值指向型改进I-M-K 材料模型作为基本恢复力模型，利用OpenSEES 有限元平台对每一RC 圆柱的试验数据进行模拟，识别出其恢复力模型参数。选取15 个RC 圆柱设计参数，建立构件的恢复力模型参数经验预测公式(值)，并对其有效性进行了验证。

1 RC 圆柱试验数据的来源及标准化

采用PEER 结构性能数据库中76 个RC 圆柱试验数据组成本文数据库。其中，所选择试件的加载方式均为拟静力低周往复加载，试件的失效模式为弯曲破坏或弯剪破坏。76 个试件的主要设计参数范围如表1 所示。

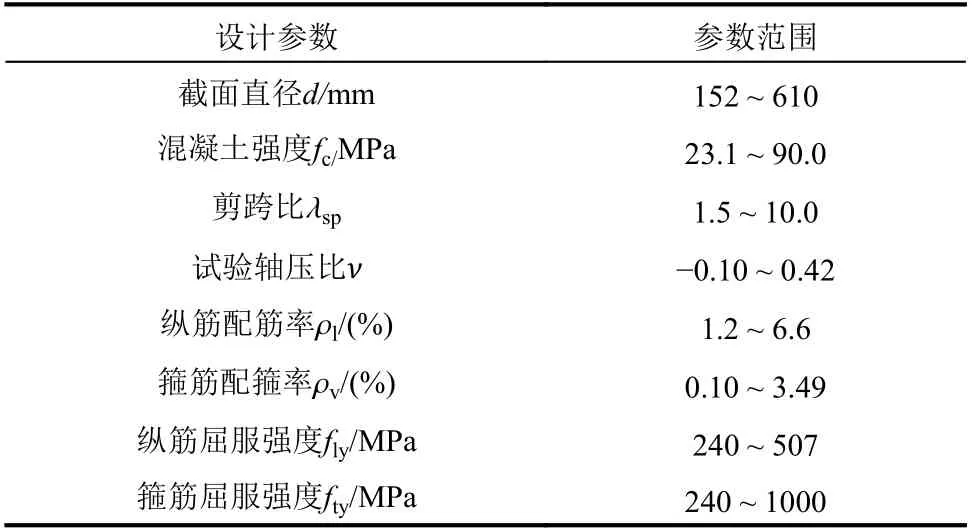
表 1 圆柱试件的主要设计参数范围Table 1 Range of main design parameters of circular columns

值得说明的是，在PEER 所提供的试验数据中，RC 圆柱包括八角形(Octagonal)和圆形(Circle)两种箍筋配筋形式。本文所选择的RC 圆柱试件均为圆形配筋。根据文献[5]，PEER 结构性能数据库将RC 柱试件根据其构造类型及加载边界条件分为5 类，并对试验数据均采用了标准化处理，统一转化为悬臂型柱(Cantilever)的力-位移数据。由于恢复力模型不同参数具有不同的灵敏度区间，且在不同坐标系下对恢复力模型进行参数识别的结果也差异较大。针对这一问题，本文参考文献[12]及文献[13]的处理方法，将所研究的RC 圆柱试验数据，在考虑P-Δ 效应后统一转化为弯矩-转角的形式。

2 峰值指向型的改进I-M-K 材料模型

文献[14]提出了一种折线型恢复力模型(I-MK 模型)，该模型可以较好地描述结构构件在往复荷载作用下的刚度和强度退化特性。Lignos 和Krawinkler[3]在I-M-K 恢复力模型基础上，在对大量钢结构构件及RC 构件试验数据的模拟基础上，进一步对I-M-K 滞回模型进行了修正(改进I-M-K模型)，重新定义了I-M-K 模型的骨架曲线中几个参数，从而减小了I-M-K 模型参数的离散性，并对其刚度和强度在循环加载过程中的退化原则进行了改进。改进的I-M-K 材料模型可分为双线型、峰值指向型和捏拢型三种。本研究选用峰值指向型改进I-M-K 材料模型，该材料可以考虑恢复力模型在正负方向的不对性。

3 RC 圆柱的滞回模型参数识别

需要说明的是，改进I-M-K 材料需识别的23个参数中的部分参数可根据已有文献取为定值。

表 2 OpenSEES 中峰值指向型改进I-M-K 滞回材料模型参数及物理意义Table 2 Parameters and physical meanings of Peak-oriented modified I-M-K hysteretic material model in OpenSEES

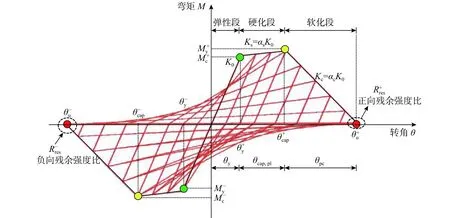
图 1 峰值指向型改进I-M-K 滞回材料模型Fig. 1 Peak-oriented modified I-M-K hysteretic material model

对于其余需识别的参数，可其分为骨架曲线参数和滞回耗能参数两类并分别进行参数识别。总体的识别流程可分为2 个阶段共5 个步骤。阶段1：基于试验数据的滞回模型骨架曲线参数的识别，识别参数屈服弯矩My(步骤1)、屈服转角θy(步骤1)、硬化段转角θcap,pl(步骤2)、峰值弯矩与屈服弯矩比a (通过硬化段刚度as·K0及硬化段转角θcap,pl计算，见步骤2)以及软化段转角θpc(步骤3)。阶段2：基于数值模拟的滞回模型耗能参数的识别(见步骤4 和步骤5)，识别参数Λ。5 个步骤的具体流程如下：

步骤1：将滞回曲线各循环之间刚度变化最大的点作为滞回模型骨架曲线的屈服点。连接滞回曲线零点与屈服点作为滞回模型骨架曲线的弹性段；

步骤2：判定滞回曲线中的首次出现随位移增长而弯矩下降(亦称为循环内退化[16])的滞回环所对应的转角，将其作为峰值点转角。若试件滞回曲线并未显示出循环内退化特征，则参考文献[11]及文献[12]将试件加载的极限位移坐标定义为试件的峰值点。随后，以屈服点为起始点，沿其所的滞回曲线的坐标点作切线，延伸至峰值点对应转角，连接峰值点与屈服点作为骨架曲线的硬化段；

步骤3：以峰值点为起始点，以峰值点处下降段的斜率作为骨架曲线软化段的斜率，连接峰值点及下降线与转角坐标轴的交点作为骨架曲线软化段；

步骤4：基于OpenSEES 有限元平台，建立RC 圆柱滞回性能模拟的集中塑性宏单元模型(见图2)。其中，零长度单元位于RC 圆柱底部，其采用改进I-M-K 材料模型进行模拟，模型骨架参数采用步骤1～步骤3 所定义的骨架点来进行定义；

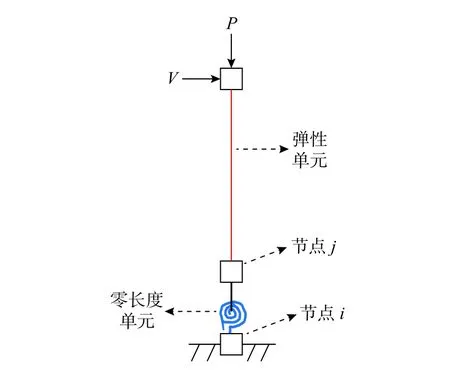
图 2 基于OpenSEES 的RC 圆柱滞回加载分析模型Fig. 2 Numerical model of RC circular columns under cyclic loadings based on OpenSEES

步骤5：基于步骤4 所建立的RC 圆柱滞回加载分析模型，不断调整循环退化参数值Λ，直至数值模拟结果与试验结果相吻合，并获得较优的循环退化参数值Λ。

对于改进I-M-K 材料模型，不同滞回耗能参数Λ 的取值会较为显著地影响RC 圆柱的滞回规则。仅以390 号圆柱为例，图3 给出了Λ=0.1、0.5和1.0 时，RC 圆柱的模拟滞回曲线及其与试验曲线的对比。由图3 可见，在相同的骨架曲线基础上，不同的Λ 取值对应的RC 圆柱滞回曲线相较大。基于上述情况，本文采用循环迭代方式对各试件的较优Λ 值进行识别，取Λ 的初始值为0.1，步长为0.05，逐级提升Λ 值直至模拟精度满足要求。图4 给出了RC 圆柱恢复力模型中较优Λ 值的搜索过程。

根据上文介绍的RC 圆柱恢复力模型参数的识别过程，分别对76 根RC 圆柱滞回加载试验进行数值模拟，获得每一RC 圆柱所对应的改进I-M-K材料模型的骨架和滞回耗能参数，如表3 所示。为了说明基于改进I-M-K 材料模型的RC 圆柱恢复力模型参数识别过程，选取两个典型RC 圆柱的识别结果进行说明，见图5(a)和图5(b)。所选取的两个RC 圆柱试件在PEER 结构性能数据库中的编号分别为390[17]和309[18]。

值得说明的是，大部分圆柱滞回加载试验数据并未出现明显软化段。为了模拟RC 圆柱在实际地震中可能出现的软化段特征，本文在定义改进I-M-K 材料模型的软化段时，根据文献[15]的方法，定义峰值点位移的下限，如图5(b)所示。

图 3 对应不同Λ 取值的RC 圆柱滞回模型参数Fig. 3 Hysteresis curves of RC circle columnwith different values of Λ

4 RC 圆柱恢复力模型参数的预测

4.1 预测方程的选择

在第3 节已获得的76 根RC 圆柱恢复力模型参数的识别结果基础上，本节进一步回归RC 圆柱的恢复力模型参数的预测公式。采用式(1)所示的方程形式来对RC 圆柱的恢复力模型参数进行预测。

4.2 预测方程的拟合流程

图 4 参数Λ 的迭代识别过程Fig. 4 Cyclic identification process of Λ

表 3 基于改进I-M-K 材料模型的76 个RC 圆柱的滞回模型参数识别结果Table 3 Identified parameters of modified I-M-K material model for 76 RC circular columns of concern

基于式(2)对RC 圆柱恢复力模型的不同参数分别进行拟合。鉴于所考虑的RC 圆柱15 个设计参数之间可能存在较强相关性，会导致多重共线性问题。因此，在拟合过程中要求其变量之间的方差膨胀因子(Variance Inflation Factor, VIF)小于10。为此，本文采用分步拟合法，对参数进行初选后，采用“只出不进”的方式[19]，通过减少输入变量，避免各拟合变量之间的多重共线性，关键步骤如下：

步骤1：将全部15 个柱设计参数对数化后作为输入变量，将对数化后的滞回模型参数作为输出变量，采用式(2)进行初步拟合；

图 5 典型RC 圆柱的参数识别流程及结果Fig. 5 Identification process and obtained hysteretic model parameters for two typical RC circular columns

步骤2：基于步骤1 中初步拟合结果中15 个输入变量的p 值，挑选p<0.05 的变量(该变量t 检验线性显著)[19]作为新的输入变量进行二次拟合；

步骤3：计算二次拟合中各输入变量的VIF值，若所有输入变量的VIF≤10[20]，则说明采用二次拟合中的输入变量拟合公式多重共线性弱，满足要求。若存在输入变量的VIF>10，则逐步删除VIF 最高的输入变量，直至所有输入变量VIF≤10；

步骤4：在步骤3 基础上，为避免过拟合情况，本文在保证公式预测精度的基础上，删除了输出参数相关性较小的输入参数，以最大程度控制输入参数数量。待输入参数确定后，记录回归方程的常数项及各变量的回归系数，完成式(2)形式拟合，随后将式(2)转变为式(1)形式，获得参数的预测公式。

4.3 模型参数的预测公式(值)

基于上文流程可给出预测参数包括屈服弯矩My、屈服转角θy、硬化段转角θcap,pl、峰值弯矩与屈服弯矩比a、软化段转角θpc，及循环退化参数Λ 的预测公式。需要说明的是，虽然试件识别出的骨架曲线参数在正负方向上显示出了一定的非对称性，但不对称程度并非特别明显。为简化起见，本文统一采用了正向的骨架参数值进行公式拟合。

4.3.1 屈服弯矩My

参考第4.2 节的拟合流程对屈服弯矩My进行经验预测公式拟合，获得预测公式为：

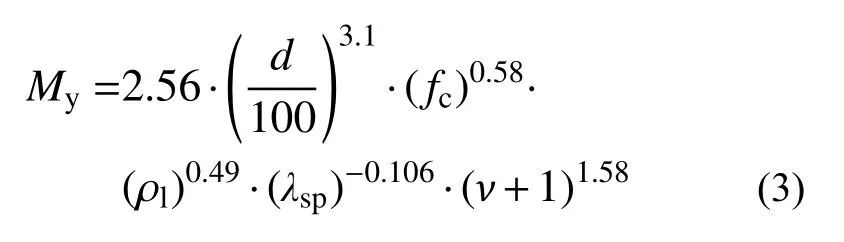
式(3)中各变量的VIF 值，如表4 所示。式(3)的拟合判定系数R2=0.97，表明式(3)的拟合结果较好。

表 4 屈服弯矩My 经验预测公式中各变量的VIFTable 4 Variable VIFs in the empirical prediction of My

图6 给出了My预测值与试验值之间的关系。预测值与试验值比值的均值为1.01，中位值为0.98。

图 6 屈服弯矩My 的预测值及试验值对比Fig. 6 Comparison of predicted values andexperimental values of My

4.3.2 屈服转角 θy

屈服转角θy的经验预测公式为：

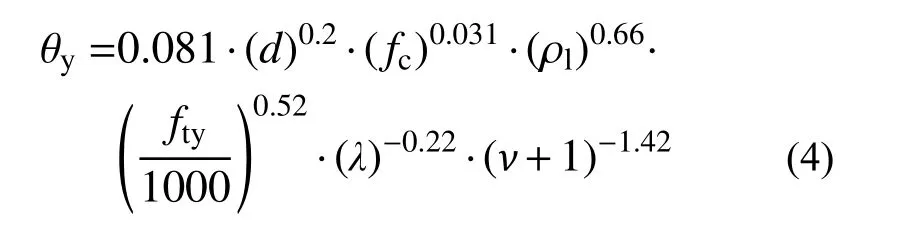
式(4)中各变量的VIF 如表5 所示，其对应的判定系数为R2=0.475。

表 5 屈服转角θy 经验预测公式中各变量的VIFTable 5 Variable VIFs in empirical prediction of θy

图7 给出了各试件采用式(4)的计算值θy_cal的预测值与试验值θy_exp与散点对比，可看出二者总体上呈线性关系，随屈服转角值提高，离散性逐渐增加，二者比值的均值为1.08，中位值为1.03。

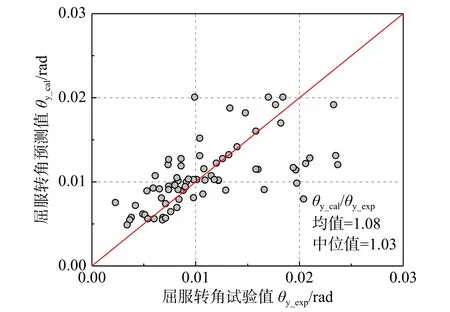
图 7 屈服转角θy 的预测值及试验值对比Fig. 7 Comparison of predicted values and experimental values of θy

4.3.3 硬化段转角θcap,pl

硬化段转角θcap,pl的经验预测公式为：

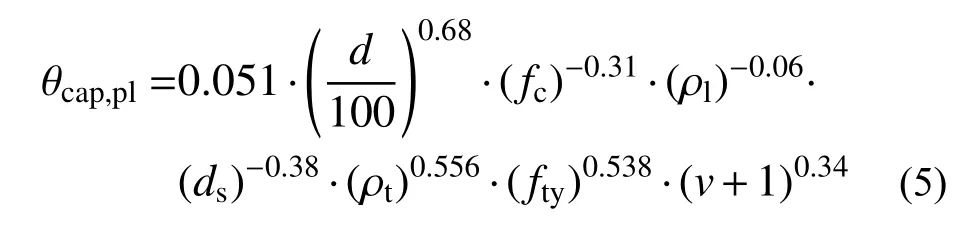
式(5)中各变量的VIF 如表6 所示。式(5)的判定系数R2=0.452。

表 6 硬化段转角θcap,pl 经验预测公式中各变量的VIFTable 6 Variable VIFs in empirical prediction of θcap,pl

图 8 对比了 θcap,p的预测值 θcap,pl_cal与试验值θcap,pl_exp。由图8 可见，多数试验结果的硬化段转角小于0.1 rad，预测值与试验值整体上呈线性关系，二者的比值的均值为1.08，中位值为0.96。

4.3.4 峰值弯矩与屈服弯矩比α

采用式(2)所示的线性方程对α 的预测方程进行拟合，结果表明：α 值与15 个设计参数之间的相关性较差。图9 为表2 中76 根试件的α 的试验值，可看出α 的取值总体较为稳定，均值为1.36，标准差为0.26。故本文取平均值1.36 作为α 的经验计算值。

图 8 硬化段转角θcap,pl 的预测值及试验值对比Fig. 8 Comparison of predicted values and experimental values of θcap,pl

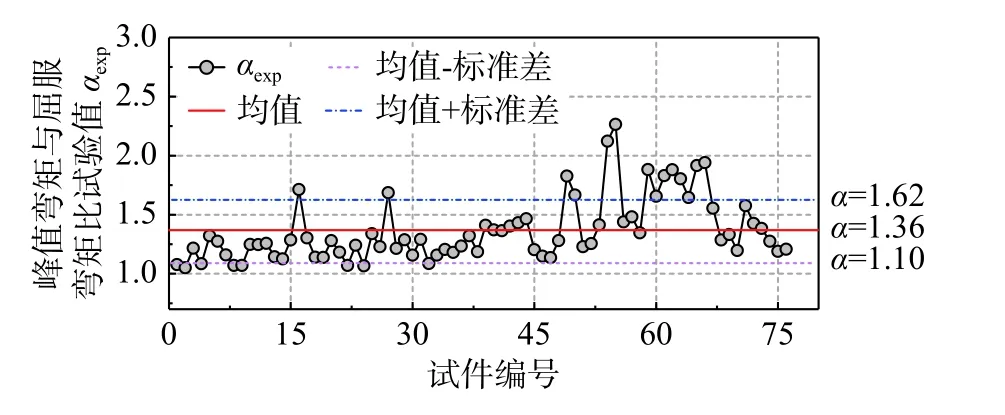
图 9 76 根RC 圆柱峰值弯矩与屈服弯矩比α 的试验值Fig. 9 Experimental values of ratios between peak moment and yield moment of 76 RC circular columns

4.3.5 软化段转角θpc

由表2 可看出，仅有5 根RC 圆柱试件的恢复力模型参数识别结果包含软化段转角，表明RC 圆柱在采用改进I-M-K 材料模拟时硬化段即已达到极限破坏状态，θpc对后续模拟结果影响很小。因参数识别时必须添加θpc的数值，本文在此建议取表2 中5 根包含软化段转角试件θpc的平均值0.13 rad，这一结论与文献[9]和文献[15]研究方柱恢复力模型时的结果(θpc=0.1 rad)较为接近。

4.3.6 滞回耗能参数Λ

滞回耗能参数Λ 的经验预测公式为：

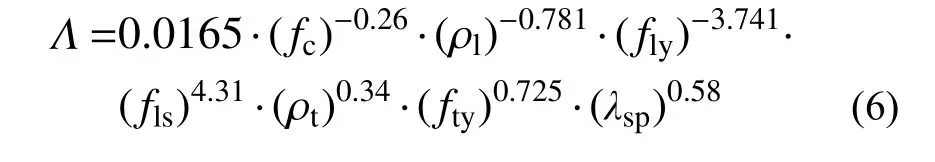
式(6)中各变量的VIF 如表7 所示，其对应的判定系数R2=0.41。

表 7 滞回耗能参数Λ 经验预测公式中各变量的VIFTable 7 VIF of variables in empirical prediction of Λ

图10 为各试件采用式(6)的得到的Λ 计算值Λcal与试验值Λexp对比结果。由图可见，试件的Λ 值介于0～10 之间，这一范围大于文献[13]中Λ的取值范围。主要原因为，本文研究的RC 圆柱中部分试件的耗能能力较强。此外，预测值略大于试验值，二者比值的均值为1.09，中位值为0.98。

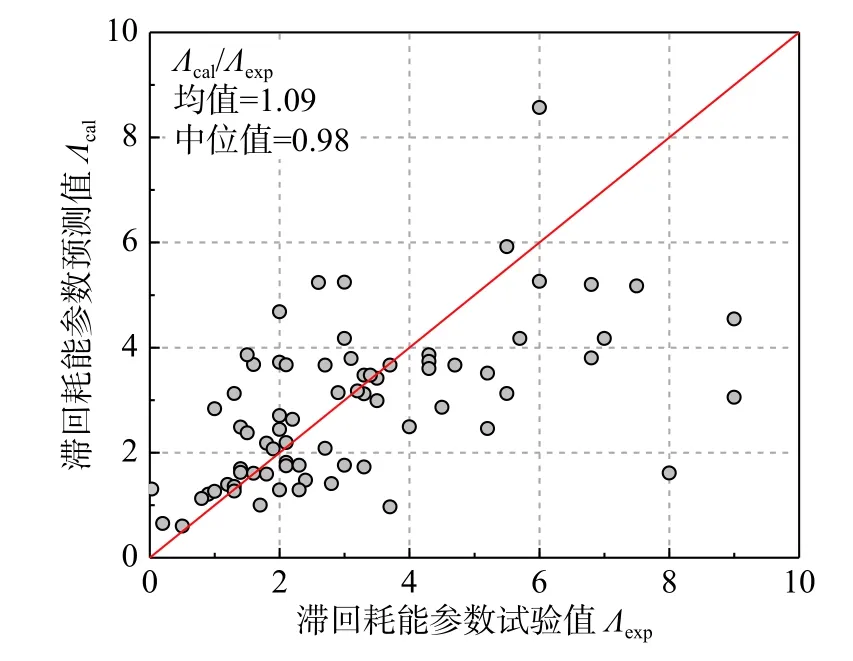
图 10 滞回耗能参数Λ 的预测值及试验值对比Fig. 10 Comparison of predicted values and experimental values of Λ

5 RC 圆柱恢复力模型参数的验证

为验证第3 节中给出的RC 圆柱恢复力模型经验预测公式及经验值的合理性，本文以文献[21]中试件A12、文献[22]中试件CA-1 及文献[23]中的试件RC3 作为验证组试件对本文识别获得的恢复力模型进行验证。上述三个RC 圆柱构件并未包含进入本文的试验数据库，因此，用其作为验证组不会出现“数据泄露”的问题。

表8 给出了验证组圆柱试件的基本设计参数，其失效模式均为弯曲破坏。基于第4.3 节获得的RC 圆柱恢复力模型参数的预测公式，结合参照组RC 圆柱试件的设计参数(表8)，计算得到参照组RC 圆柱恢复力模型参数的计算值，如表9 所示。基于所获得的参照组RC 圆柱恢复力模型参数的计算值，获得验证组柱试件的滞回曲线，并将其与试验结果进行对比，如图11 所示。由图11可见，基于本文提出的经验公式的模拟结果与试验结果具有较高的吻合程度。考虑验证组试件在直径、混凝土强度、配筋率、轴压比等重要设计参数的差异性，本文提出的基于改进I-M-K 材料模型的恢复力模型参数预测方程可准确的预测出RC 圆柱试件在不同设计工况下滞回曲线的强度值及滞回特征的变化规律。

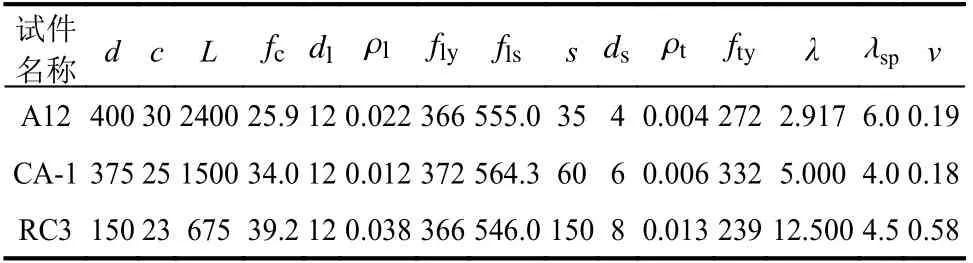
表 8 验证组柱试件的设计参数Table 8 Design parameters of column specimens in verification group

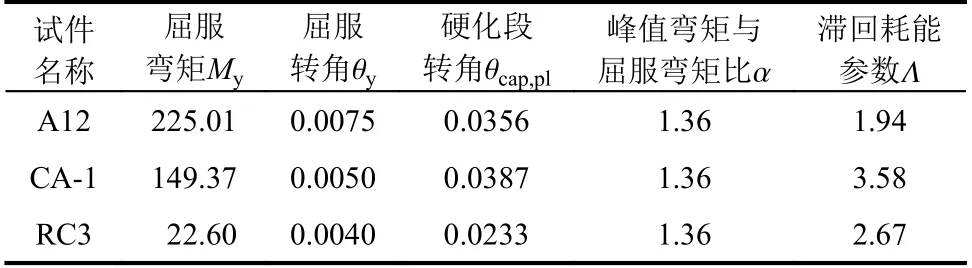
表 9 验证组柱试件基于经验公式的改进I-M-K 参数计算值Table 9 Calculation results of modified I-M-K parameters based on empirical equations

图 11 验证组试件试验与模拟结果对比Fig. 11 Comparison of test and simulation results of column specimens in verification group

6 结论

本文基于PEER 结构性能数据库中76 个RC圆柱滞回试验数据，基于改进I-M-K 材料模型，利用OpenSEES 有限元平台，对RC 圆柱的恢复力模型参数进行识别，并获得滞回模型骨架参数及滞回耗能参数的预测方程。本文结论如下：

(1) 本文提出的方法可以较好地识别出RC 圆柱的恢复力模型参数。基于所识别出的改进I-M-K恢复力模型可以很好地模拟RC 圆柱在滞回加载过程中的强度及刚度退化特征；

(2) 在对数坐标系下，采用多元线性回归方程可很好的拟合出屈服弯矩My、屈服转角θy、硬化段转角θcap,pl、滞回耗能参数Λ 的经验预测公式。其中屈服弯矩My拟合精度最好，其判定系数为0.97；

(3) 峰值弯矩与屈服弯矩比α 的取值与设计参数无明显关联，本文研究推荐取所有试件的平均值1.36。绝大部分试件的参数识别结果不含软化段转角θpc，本文研究推荐取可校准出θpc段的试件的平均值0.13 rad；

(4) 对比基于本文经验公式得到的对照组试件滞回曲线及试验滞回曲线，可看出，本文提出的RC 圆柱经验公式/经验值可很好的预测出RC 圆柱的在滞回循环中的强度值及滞回特征变化。

值得指出的是，本文所采用的钢筋混凝土圆柱试件的失效模式均为弯曲破坏或弯剪破坏。因此，本文所提出的恢复力模型仅适用于弯曲破坏和弯剪破坏的钢筋混凝土圆柱。由于失效模式为剪切破坏的钢筋混凝土柱的滞回性能与弯曲破坏或弯剪破坏柱的滞回性能差异性较大，因此，本文所提出的恢复力模型并不适用于剪切破坏圆柱。