多重四边形环索-张弦穹顶局部断索冲击分析

张 超，付馨迪，杜修力，颜学渊，许 莉，贾宏宇

(1. 福州大学土木工程学院，福建，福州 350108；2. 北京工业大学城市与工程安全减灾省部共建教育部重点实验室，北京 100124；3. 西南交通大学土木工程学院，四川，成都 610031)

弦支穹顶结构是在单层网壳和索穹顶的基础上发展起来的一种新型预应力大跨度结构体系，被广泛应用于体育场馆、会展中心等大型公共建筑中[1]。拉索是弦支穹顶的核心构件，在实际使用过程中，可能会因施工偏差，遭遇爆炸、撞击等发生局部拉索失效[2−3]。从而使结构的刚度减小，导致一系列连锁反应继而发生局部或整体倒塌[4−6]。由于承受巨大预张力，拉索失效时间通常较短[7−8]。拉索短时间瞬断会迅速释放大量的应变能，进而引起剩余屋盖结构的剧烈振动，甚至发生局部或整体倒塌[9]。朱明亮等[10]基于向量式有限元的弦支穹顶的断索分析研究表明，拉索瞬断引起的动力放大效应十分显著；Shekastehband 等[11]对全张拉体系中的拉索突然破断进行了理论分析和试验研究，发现不同区域的拉索破断产生的影响完全不同，严重情况下甚至会引起张拉整体结构的连续倒塌；宗钟凌等[12]对一直径6 m 的葵花型索穹顶模型进行单根拉索瞬断试验表明：不同位置拉索的失效对结构的影响程度不尽相同，外环斜索和脊索的破断对结构影响相对较大。总体而言，断索引起的动力冲击动力效应不能被忽视。

目前，常用断索计算方法是基于荷载等效路径法的静力分析方法，其动力冲击效应则采用动力放大系数(dynamic amplification factor，DAF)来进行描述[13−14]。该方法概念简单，计算方便，被广泛应用于断索分析中，并被目前多个行业规范所推荐使用。基于单自由度体系动力放大响应[15]，相关规程或技术标准均给出了DAF 的最大值。如，针对建筑结构抗连续塌，GSA (general services administration)[16]及DOD (Department of Defense)[17]均给出了动力放大系数的取值为2.0；针对断索冲击，美国 P.T.I.(Post-Tensioning Institute)也提出2.0 为最大值。然而，部分学者对于断索冲击的研究结果表明：统一采用DAF=2.0 的取值，在某些情况下是不安全的。Mozos 等[18]对10 个典型的斜拉桥进行了断索分析，指出统一采用同样的DAF数值来进行简化计算是不合适的，且部分构件的DAF 可能大于推荐数值2.0。Zhou 等[19]同样指出统一采用2.0 的DAF 取值在某些情况下是不安全的，且具有一定的局限性。王霄翔等[20]开展的弦支穹顶局部断索试验表明，不同类型的拉索失效引起的动力放大系数均可能大于2.0。

多重四边环索-张弦组合穹顶结构为新型弦支体系，采用多重四边环索和布置于两端的张弦索体系，形成下部柔性拉索体系，大大提高了单层网壳结构的承载力[21]，目前已经应用于福州市海峡奥体中心体系馆设计中。由于多重环索和张弦索通过网格梁和撑杆相互影响，因此，多重四边环索-张弦组合穹顶较传统弦支穹顶更为复杂。目前，断索冲击效应的研究多仅针对传统索穹顶结构，而不同类型拉索瞬断对于多重环索-张弦穹支屋盖的影响规律还不明确[22]。因此，本文拟研究适用于此类复杂穹支屋盖在弹性阶段断索冲击下的动力响应分析方法及分析参数；进一步揭示弹性断索冲击下多重环索-张弦穹支屋盖的动力响应规律，并评估规范推荐使用的DAF=2.0 的等效静力分析方法的适用性。最后，探讨不同位置、类型及数量的拉索瞬断对动力冲击效应的影响规律。

1 多重环索-张弦组合弦支穹顶

1.1 数值模型建立

作为一种特殊的弦支穹顶屋盖，多重四边环索-张弦组合屋盖的下部柔性索体系由三重四边环索(内环、中环和外环)和张弦索共同组成。此新型弦支屋盖已经被成功应用于福州奥体中心体育馆[23]。本文以该体育馆为研究背景，如图1(a)所示。其中，张弦-三重四边环索体系的主要设计参数如下：第一环(内环)的撑杆高度为9.0 m，两方向环索长度分别为21.6 m、19.0 m，斜索长度为13.9 m、15.0 m；第二环(中环)的撑杆高度为9.0 m，环索长度为37.9 m、36.0 m，斜索长度为13.4 m、14.85 m；第三环(外环)撑杆9.5 m，两方向环索长度分别为56.9 m、51.1 m，斜索长度为15.8 m、18.2 m；张弦索设置在东、西两侧，拉索长度为75.55 m，撑杆高度分别为8.5 m、11.0 m。正常运营状态下，屋面盖板等二期附加荷载集度为 0.823 kN/mm2，设计活载为 0.5 kN/mm2。网格梁、屋面支撑、竖向撑杆等型钢构件均采用Q345B 钢材，钢材弹性模量为2.06×1011N/m2，屈服强度为210 MPa；预应力拉索的弹性模量为1.95×1011N/m2，设计抗拉强度为1670 MPa。基于SAP2000 建立屋盖结构的三维空间数值模型。其中，网格梁、屋面支撑及竖向撑杆均采用框架(Frame)单元模拟；环索及斜索均采用拉索(Cable)单元模拟。由于撑杆与网格梁、拉索的连接更接近于铰接，因此，在数值模型中把模拟撑杆的Frame单元两端转角约束释放。

1.2 数值模型验证

为方便后文表述，对拉索体系及屋盖体系进行编号。拉索体系的编号规则如下：第一个字母代表拉索类型(H 代表水平索，X 代表斜索)，第一个数字代表水平环索位置为内环(1～4 依次代表内环、中环、外环和张弦索)，第二个数字代表该环索中的拉索编号。以图1(b)中H12 为例，其代表内环中第二根水平索。屋盖关键节点编号如图1(c)所示。

为了验证本文所建立数值模型的准确性，以背景工程在施工过程实际监测数据为比较。采用“短链杆温降收缩”模拟屋盖实际施工过程中各级拉索张拉工况，数值模拟得到网格梁应力和屋盖节点挠度与监测数据的对比分别如图2 所示。从图2(a)可以看出，数值模拟的网格梁应力与监测数据在大部分测点均较好地吻合。从图2 (b)的位移对比可以看出，模型计算位移值略大于实测数据，最大差值约为1 cm，位于6 号节点。由于篇幅有限，其余监测结果对比详见文献[21]。总体而言，针对不同施工阶段，数值模拟与实际监测数据总体吻合较好，误差均在可以接受的范围内。因此在后续的分析中，以此数值模型为基准分析模型。

2 断索冲击的动力分析方法

2.1 断索冲击模拟方法

图 1 多重四边环索-张弦组合弦支穹顶结构Fig. 1 The multi-loop cable-string dome

拉索瞬断前后，弦支屋盖结构受力状态变化过程如图3 所示。拉索瞬断冲击下动力响应本质上是冲击荷载下的断索后屋盖结构的受迫振动过程。因此，可以把分析过程简化为针对断索后的屋盖结构进行受冲击荷载下的动力响应分析。针对网架结构体系中的构件失效，蔡建国等[24]提出了一种能考虑初始状态的等效荷载瞬时卸载法，该方法可在一个计算过程中同时模拟构件失效前整体结构的初始状态和构件的后续突然失效过程。

图 2 数值模拟与监测数据对比Fig. 2 Comparison of numerical and monitoring data

基于以上思路，本文拟使用等效荷载瞬时卸载法模拟多重环索-张弦组合弦支体系在断索冲击下的动力响应，即把原拉索作用以等效荷载的方式施加，在等效初始模型的基础上，把拉索失效过程等效为原索力的卸载。具体实现步骤如下：首先，得到完整屋盖的等效模型，即先对完整屋盖结构进行静力分析，得到断索前拉索的轴拉力P0；其次，去除失效拉索，并在原拉索两端节点施加相应的等效轴拉力P0，即得到完整屋盖的等效模型；再次，在等效模型中，在拉索两端节点施加与P0反向的荷载时程P(t)=P0f(t/t0)，模拟断索冲击作用。其中，f(t/t0)为[0, 1]之间随时间变化的函数，称为拉索失效路径；最后，进行P(t)荷载作用下动力时程分析，得到剩余屋盖结构的动力响应。具体的分析流程如图3 所示。

2.2 初始等效模型验证

根据图3 的分析流程图，初始状态等效模型的后续断索冲击动力响应的基础，即初始状态等效模型的准确性直接影响了后续冲击效应的分析结果。因此，本节对本文拟采用的完整屋盖等效模型的准确性进行验证。对于弦支穹顶结构来说，外圈的1 圈～2 圈环索起控制作用[25]。因此，本节以外环索H31 失效为例，验证本文所建立的多重四边环索-弦支穹顶屋盖等效模型的准确性。

图 3 拉索瞬断的发生过程及等效方法Fig. 3 The process and equivalent method of sudden cable failure

图 4 完整屋盖与等效屋盖的响应值比较Fig. 4 Comparison of intact roof and equivalent roof

基于完整屋盖结构的静力分析结果，自重作用下外环索H31 的轴拉力为2284 kN，其余拉索索力如图4(a)所示。因此，在等效模型中，去除失效拉索H31，在原拉索两端沿轴向施加反方向轴力2284 kN，即得到等效模型。等效模型和完整结构的索力、位移及振型对比分别如图4(a)、图4(b)、图4(c)所示。从中可以发现：在等效模型中，除了失效索H31 外的其他拉索索力均与完整屋盖十分接近；其中，对于拉力最大的拉索H34，轴力误差仅为1%。图4(b)中屋盖挠度对比也可以看出，等效模型的屋盖变形响应与完整屋盖几本一致，其中跨中节点的位移为完整结构仅相差3 mm，误差约为6%。图4(c)、图4(d)分别列出来完整结构和等效模型的第一阶振型图。初始状态等效模型的第一阶振型表现为沿南北向屋盖竖向对称振动、沿东西向屋盖竖向反对称振动。此振动形态与完整屋盖完全一致。从基本振型的自振周期均为1.126 s。

基于以上对于内力、位移和动力特性的比较结果可看，本文采用拉索等效拉力代替实际拉索的等效方法是可行的。即，可以认为本文得到的初始状态等效模型可以精确地反应完整屋盖结构的静力和动力性能。因此，后文基于此初始状态等效模型开始后续的动力响应分析。

2.3 动力分析参数研究

有关学者针对斜拉桥断索的研究结果表明：断索持续时间t0、失效路径f(t)等参数均对冲击动力效应有很大影响[26]。因此，本节以外环索H31瞬断为例，探讨断索持续时间t0、断索失效路径f(t)、初始荷载组合W、结构阻尼系数ζ 等参数对四边环索-张弦屋盖的断索冲击效应的影响。

本文采用动力放大系数DAF 来反映断索冲击引起的屋盖响应的放大程度。以位移响应为例，动力放大系数DAF 定义为：

式中：S0为断索前屋盖的位移值；Ss为拉索失效后屋盖达到最终静止状态位移值；Sd,max为屋盖振动过程中的位移响应最大值。

2.3.1 断索失效路径

在讨论断索持续时间之前，本文首先探讨不同的断索失效路径f(t)对屋盖结构动力响应的影响规律。本文对比分析了9 种不同的拉索失效路径，如阶跃函数、指数函数f(t)=(t/t0)α及线性函数，其数学表达式如表1 所示。其中，路径1 和路径9 为阶跃函数；路径5 为线性函数；路径2～路径4 为α<1 的指数函数，α 越小，时间前期变化率越大；路径6～路径8 为α>1 的指数函数，α越大，在时间后期函数变化率越大。为了更直观地表达出失效路径，本文以断索持续时间t0进行时间正则化处理，得到以时间比t/t0为横坐标的断索失效路径示意图，如图5 所示。

不同断索失效路径下，屋盖跨中节点JZ 的位移放大系数如图 6 所示。当断索时间 t0小于0.05T 时，由于失效时间较短，不同断索失效路径均会引起较大的DAF 值(DAF=2.38)，即不同的断索失效路径对于断索冲击效应没有影响。但是，当拉索失效时间t0大于0.05T 时，不同断索失效路径会引起位移DAF 有较大的差别。以断索持续时间 t=0.5t0为例，路径1～路径9 对应的DAF 分别为 2.00、1.84、1.73、1.42、1.62、1.78、1.92、1.98、2.00。按DAF 由大到小排列，工况依次为：路径9=路径1>路径8>路径7>路径2>路径6>路径3>路径4>路径5。可以得到以下规律：1) 当索力按阶跃函数变化时(路径1、路径9)，不管何时发生阶跃变化，均为最不利拉索失效工况，会导致最大DAF 值；当索力按线性函数变化时(路径5)，为最缓和的索力变化路径，导致的DAF 值较其他路径均更小；当索力按指数函数变化时，DAF 值介于阶跃函数(路径1、路径9)和线性函数(路径5)之间；即，引起的DAF 值由大到小依次为：阶跃函数>指数函数>线性函数；2) 当索力按指数函数变化时，不管指数α 是否大于1，均表现为变化率越大的失效路径引起更显著的DAF，如路径8>路径7>路径6，路径2>路径3>路径4。总体而言，不同的拉索索力失效路径具有不同的拉索索力变化率，进而会引起结构动力放大系数DAF 的不同。当索力变化率较大时，通常会引起较大的DAF 值。3)当拉索按失效路径5 失效时，当 t0∈[ T , 10 T ]时，冲击放大系数 DAF 随 t0的增加，呈现周期性变化规律，如图 7 (a)所示：即当 t0/ T 接近整数时，冲击放大系数 DAF 处于波谷；当 t0/ T 接近两个相邻整数的中点时，冲击放大系数 DAF 则处于波峰。此现象可以由图 7(b)来解释，断索冲击下剩余结构发生自振周期为 T 的竖向振动。当断索冲击荷载与振动同向时( t0= T )，冲击荷载与振动同步起了加强作用，反之，荷载和振动异步，则起来减弱的反作用。当t0=1.5 T时，由于 t ∈[ T ,1.5 T ]的时间区间，荷载与振动同步而导致更大动力放大效应。本文的分析结论与文献[27]针对斜拉桥断索的研究结论是一致的。

表 1 失效路径函数f(t)Table 1 The function of cable failure paths

图 5 不同断索失效路径Fig. 5 Different cable failure paths

图 6 节点JZ 位移放大系数Fig. 6 DAFs of joint JZ

图 7 路径5 断索冲击与屋盖振动的关系Fig. 7 The relationship between the impact at failure path 5 and roof vibration

然而实际过程中拉索失效过程并非是理论瞬断(如路径1、路径9)，而是变化率逐渐变大的过程。鉴于指数函数(α>1)先缓后陡的变化趋势与实际拉索失效过程较为接近，同时基于偏不利情况考虑，因此后文断索冲击分析中拟采用表1 中的路径8 作为拉索失效函数。

综上所述，断索持续时间t0对于冲击效应的影响较大。文献[27]开展了一系列拉索断裂试验，结果表明拉索破坏的持续时间t0为0.0055 s，此数值仅为本文多重环索屋盖自振周期T(1.148 s)的0.005 倍。由于实际拉索持续时间t0远小于0.05T，因此，可以认为取t0=0.0055 s 可以得到断索冲击下动力响应最不利值。

2.3.2 屋盖初始荷载

为探讨屋盖初始荷载对断索冲击效应的影响，本文基于《建筑结构荷载规范》(GB 5009−2012)[28]得到屋盖5 组不同的屋面荷载组合，其中，组合1 为“1.0 恒载+1.0 活(雪)载”，组合2 为“1.0 恒载+1.0y 向风”，组合3 为“1.0 恒载+1.0x向风”，组合4 为“1.0 恒载+1.0 升温”，组合5为“1.0 恒载+1.0 降温”。荷载组合形式如表2 所示。本节主要探讨在5 种不同的屋盖荷载组合下，拉索瞬断对屋盖结构动力响应的影响。表2列出了外环索H31 失效后，屋盖节点JS4 的初始阶段位移、静力失效位移、动力位移最大值及DAF 值。

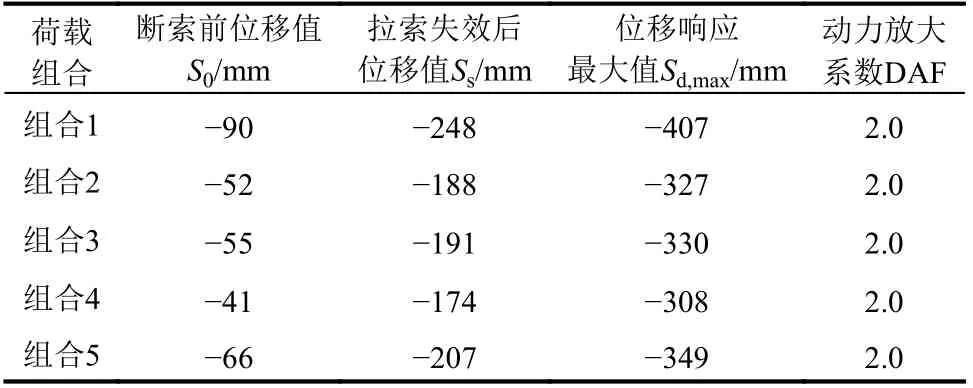
表 2 不同屋盖初始荷载下屋盖位移及DAFsTable 2 Displacements and DAFs under different initial loads of roof

可以看出：1) 断索引起的位移响应绝对值由大到小排列依次为：组合1>组合5>组合3>组合2>组合4。因此，从位移响应的绝对值来看，在荷载组合1 作用时，拉索失效会产生最大的位移响应；其中，断索引起静力变形和动力变形分别为248 mm 和407 mm；2)然而，虽然不同荷载组合下的位移响应绝对值不同，但是，不同荷载组合下的位移动力放大系数DAF 数值是一致的(DAF=2.0)，即断索冲击效应是相同的。

以上分析结果表明：在不同屋面荷载组合下，拉索瞬断引起的冲击放大效应是一致的。即，屋盖初始荷载对研究断索动力冲击效应没有影响。因此，后文弹性断索冲击分析中，取屋盖结构的正常使用阶段荷载按“1.0 附加恒载+1.0 活载”(组合1)来考虑。

需要注意的是，根据文献[29]的研究结论，当屋盖的截面应力较大，屋盖结构进入塑性受力状态时断索冲击效应则与屋盖初始荷载有关，因此，本文的研究仅针对于断索冲击的弹性动力响应。

2.3.3 结构阻尼系数

为探究结构阻尼比对穹支屋盖断索冲击响应的影响，本节分别对比分析了阻尼比ζ 为0.02、0.03、0.04 及0.05 时，外环索H31 断索冲击下多重四边环索屋盖的动力响应。不同阻尼比ζ 工况下，屋盖跨中节点JZ 的竖向位移时程曲线如图8 中所示。

图 8 不同阻尼比的位移响应时程Fig. 8 Displacement response based on different damping ratio

可以看出：不同的结构阻尼比，对断索冲击后的屋盖结构的振荡周期没有影响，也不会影响屋盖的最终静止位移Srest。但是，结构阻尼比对冲击后屋盖振动幅值有影响。由于不同阻尼比意味着体系耗能能力差异，当阻尼比较小时，断索冲击会导致较大的动力位移，当ζ=0.02 时，Sdyn=−386 mm，是ζ=0.05 时的1.2 倍；同时，当阻尼比较小时，每个振荡周期耗能能力较差，屋盖结构需要经过较长时间的振荡才能恢复静止状态。当ζ=0.02 时，断索冲击后需要振荡10 s 左右，才能基本恢复静止。

鉴于本文研究的穹支屋盖均为钢结构，因此，断索冲击动力响应分析中，取结构阻尼比ζ=0.02，为较不利的分析工况。

3 断索冲击下屋盖动力响应分析

3.1 断索后剩余屋盖的动力特性

为考虑重力刚度和应力刚化效应，断索冲击时程分析在静力分析的基础上进行。考虑“1.0 附加恒载+1.0 活载”荷载组合作用下，弦支穹顶的拉索预应力的刚度效应。在静力分析基础上，基于等效荷载法模拟外环索H31 瞬断过程。断索冲击下屋盖动力响应分析采用直接积分法，阻尼采用瑞利阻尼形式。

本文基于Ritz 向量法分析了不同重环索失效后屋盖的动力特性。图9 为不同环索失效后的剩余结构的基本振型及自振周期T。与图4(c)对比可知，不同重环索失效后，剩余屋盖结构基本振动形态与断索前完整屋盖的振型大致相同。但是，断索后屋盖结构的基本周期T 会不同程度大于完整屋盖(T=1.126 s)。基本周期由大到小依次为：张弦索失效>内环索失效>外环索失效>中环索失效>完整屋盖。由于断索冲击响应本质为断索后剩余结构的自由振动。因此可以推测出，不同类型拉索瞬断冲击后剩余屋盖结构的动力响应会有较大的差异。

3.2 断索冲击下剩余屋盖的动力响应

本节仅以外环索H31 瞬断为例，探讨环索瞬断后屋盖结构的动力响应规律。图10 (a)、图10(b)、图10(c)为外环索H31 瞬断后，剩余屋盖结构的节点位移、拉索索力、上弦杆轴力时程图。当H31失效后，空间位置较接近的张弦索H41 的索力剧增：由断索前的2548 kN，瞬间增加，达到3031 kN(为破断荷载的23%)，但是随着自由振动的衰减，最后索力恒定为2847 kN。由图10 (b)中节点JS4竖向位移曲线可以看出，断索前节点位移为90 mm，断索冲击下该节点位移最大达408 mm，屋盖静止后节点位移为248 mm；图10 (c) 的应力时程曲线看，杆件a 断索前压应力为9 MPa，由于断索冲击作用，产生的最大压应力达到46 MPa，振动停止后压应力达到31 MPa。

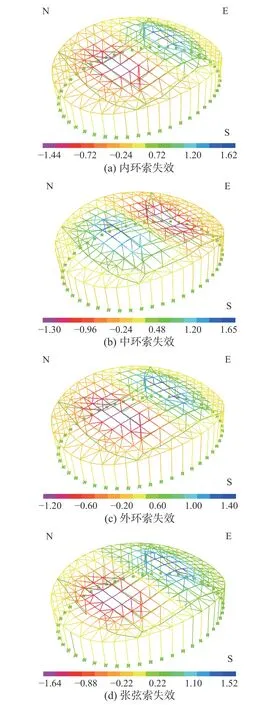
图 9 不同拉索失效后屋盖结构基本振型Fig. 9 Fundamental mode of different cable failure

以上结果均表明，拉索瞬断会对剩余的穹顶屋盖产生较大的冲击效应，屋盖中各构件的内力、位移响应均发生较显著的动态变化。断索冲击下，穹支屋盖动力响应的最大值均会显著大于最终静止响应。因此，断索冲击引起的动力放大效应对穹支屋盖结构不能被忽略。由于屋盖网格梁的总体应力较小，远小于Q235 钢材的抗压强度设计值，因此，本文主要针对位移响应进行动力分析。

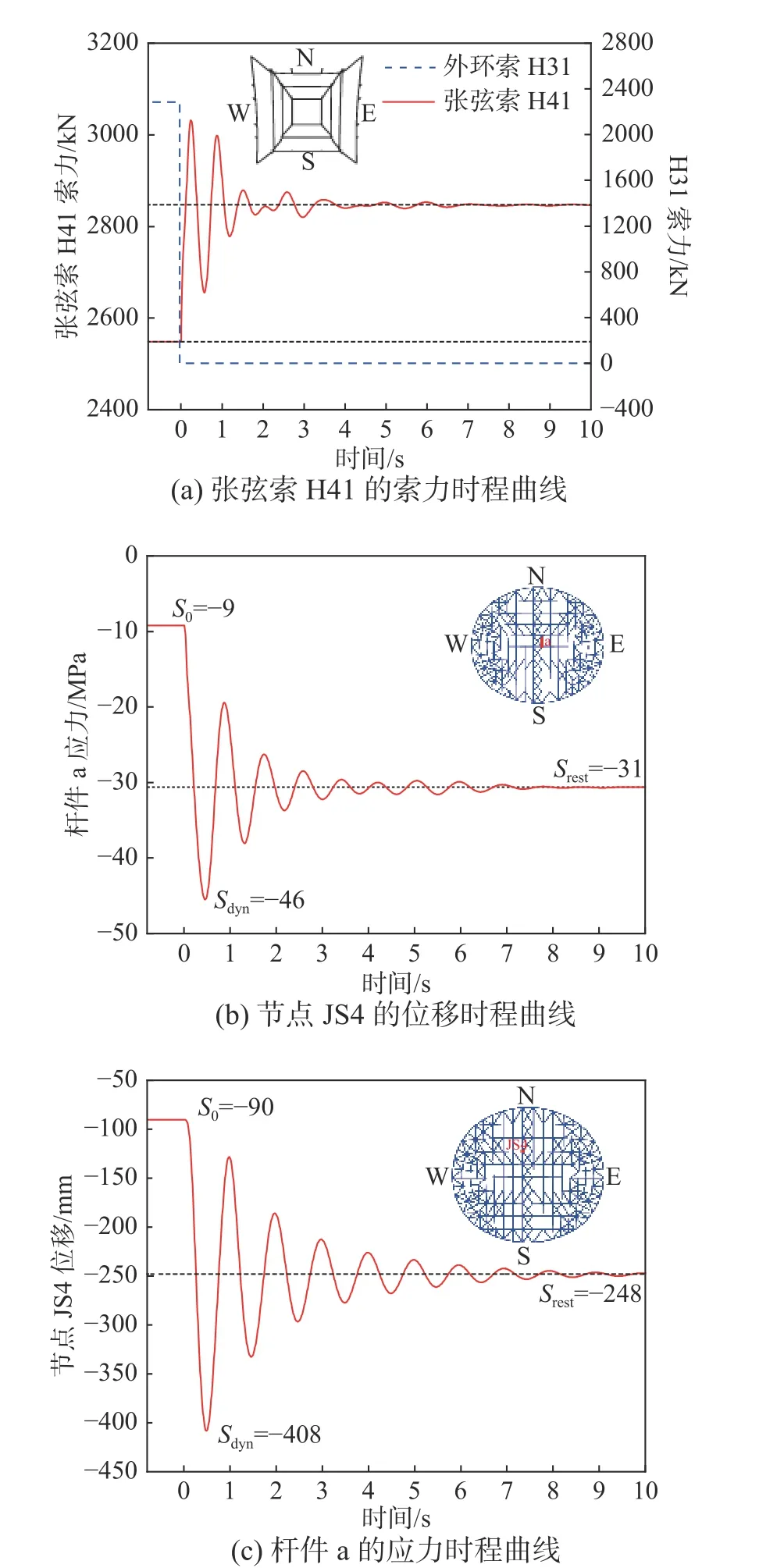
图 10 外环索瞬断冲击下屋盖动力响应Fig. 10 Dynamic response of the outer cable sudden failure

下文以穹支屋盖结构的跨中关键节点位移响应为主要研究对象，图11(a)、图11(b)分别列出了沿东西向和南北向跨中节点的动力位移峰值，图中简称为动力分析。目前，抗连续倒塌分析的较常用方法是等效静力法，也称荷载路径变换法(AP 法)[30]。此方法操作简单，广泛用于初步计算中。为了考虑断索冲击的放大效应，目前各国相关规范大多推荐采用乘以动力放大系数(DAF)以考虑动力冲击效应，并推荐DAF 最大取值为2.0。因此，本文分别采用以上两种方法计算得到断索后屋盖结构的位移响应，结果也列于图11(a)、图11(b)中，在图中分别简称为：AP 法和规范方法。

图 11 屋盖中间节点位移及位移DAFsFig. 11 Displacements and DAFs of intermediate joints

由图11 中的AP 法结果与动力响应对比看出：AP 法的屋盖位移响应的分布规律与动力分析的基本相同，但是AP 法得到的位移值远远小于动力分析结果，如AP 法计算得到的JS5 点位移为240 mm，仅为动力响应结果的58%。因此，仅考虑拉索静力失效的AP 法虽然能大致反应断索后位移响应分析规律，但是会很大程度地低估断索引起的动力放大效应。

由图11 中的规范方法的位移结果可以看出：相比AP 法，通过乘以DAF=2.0 的断索动力放大系数后，规范计算得到位移值与动力分析结果更为接近。但是，对于部分节点，规范方法计算得到的位移响应仍然小于动力分析结果，其中包括位移较大的跨中节点，如节点JS5，规范方法得到的位移为383 mm，为动力分析结果的93%。因此，采用规范方法(DAF=2.0) 不能反映实际动力响应的最不利工况，也会低估部分关键节点响应，因此需要谨慎对待。

3.3 断索冲击动力放大系数

3.3.1 动力位移放大系数

由图11(a)、图11(b)前文分析可知，目前规范[17−18]推荐的DAF=2.0 的取值，并不能反映断索冲击下的最不利状况。因此，有必要系统地探讨断索冲击作用下，多重环索-张弦穹顶屋盖的DAF 分布规律。根据公式(1)可以计算得到各节点的位移DAF值，如图11 (a)、图11(b)所示。可以看出：1) 在图11(b)中，外环索瞬断冲击下，东西向屋盖节点位移DAF 均大于2。DAF 最大值发生在节点JH13 附近，高达3.8，所幸的是，该节点位移绝对值较小。但是，位移绝对值较大的屋盖中间节点，如节点JZ、JH7-JH11，DAF 值也均明显大于2.0。因此，外环索瞬断冲击会使得屋盖东西向节点产生大于2.0 的位移放大，鉴于此类节点本身的位移绝对值已较大，要特别注意此类节点的动力响应。2) 图11(b)表明，并非所有南北向节点的位移DAF 均大于2.0，具体表现为：由跨中到两端，DAF 值逐渐减小。其中，位移响应较大的跨中节点(JS5, JZ, JS6)的DAF 均大于2.0。因此，在断索冲击下的动力响应分析应特别关注。此结论与文献[21]对于弦支穹顶的拉索瞬断试验结果是一致的。

3.3.2 动力内力放大系数

图12 分别列出了屋面关键构件的动力内力放大系数分布图，分别为网格梁轴力、撑杆轴力和拉索拉力。从图12 可以看出：1) 图12(a)中，外环索H31 瞬断冲击下，屋面网格梁的内力DAF 在外环撑杆以内区域存在大于2 的情况，在外环撑杆以外区域小于2；2) 图12(b)、图12(c)中，外环索H31 瞬断冲击下，外环索已经全部失效，没有动力响应，因此外环撑杆和拉索的内力DAF 均为1.0，中环和内环索区域的撑杆和拉索的内力DAF均大于2，张弦区域的撑杆和拉索的内力DAF 均小于2；3) 从内力DAF 的数值上看，对于拉索体系，中环区域>内环区域>张弦区域。

图 12 关键构件的轴力响应的DAFsFig. 12 Internal force DAFs of some key components

以上分析结果表明：断索冲击引起的部分位移和内力放大系数DAF 均会显著大于规范推荐系数DAF=2.0。这是因为，目前规范中的DAF 最大值是基于单自由度体系得到的[15]。然而，本文所研究的穹支屋盖结构是复杂的多自由度体系。而文献[31]基于动力学方法，推导了多自由度体系的动力放大系数表达式，证明了断索冲击动力放大系数可能会会大于2.0。因此，基于单自由度体系的规范推荐DAF=2.0 的取值并不能适用于复杂穹支屋盖这类典型的多自由度体系的断索冲击分析。采用规范推荐的“DAF=2.0 的等效静力分析方法”会明显低估断索冲击放大效应。对于此类复杂穹支屋盖结构，推荐采用动力分析方法计算拉索瞬断的动力响应。

4 不同拉索瞬断下的冲击效应研究

由前文分析可知，本文所探讨的穹顶屋盖中各构件的应力水平均较低，而屋盖竖向变形为较显著的响应。因此后文分析将重点探讨论断索冲击引起的动力位移放大系数。

4.1 同一环索中不同拉索瞬断的冲击效应

本文对比分析了外环索中水平索H31(南北向)和H32(东西向)瞬断下穹支屋盖的位移响应，如图13(a)所示。同一重环索中不同布置方向索(H31、H32)破断后，屋盖在关键节点处的竖向位移峰值曲线分布图完全重合。即，同一重环索中，不同布置方向的拉索瞬断并不会影响动力放大效应。

图 13 同一环不同拉索瞬断后屋盖结构的位移响应及DAFs 比较Fig. 13 Displacements and DAFs comparison for sudden failure of different cables in the same-loop

同时，本文还对比分析了X31(斜索)和H31(水平索)瞬断下屋盖的位移响应，如图13(b)所示。可以看出，不同布置角度索(H31、X31)破断引起的节点位移分布曲线完全重合。即，同一重环索中拉索的不同倾斜方向也不会影响穹支屋盖结构的断索冲击响应。这是因为本文所研究的四边环索屋盖的撑杆为柔性设计，撑杆两端连接均为铰接。本文分析结果与文献[13]、文献[21]的断索试验结果是一致的。综上所述，同一重环索中任一根拉索瞬断下的动力响应分析结果是一致的。

4.2 不同重环索中拉索瞬断下的冲击效应

图 14(a)、图 14(b)为内环索 H11、中环索H21 和外环索H31 瞬断引起的动力位移响应最大值。从位移响应峰值来看，位移响应最大是由外环索瞬断引起，其次为内环索，最小是中环索。从DAF 数值上看，对于大多数节点位移而言，内、中、外环索瞬断后引起的DAF 均会大于2，说明环索瞬断冲击的影响不可忽视。对比各环索瞬断工况，虽然内环索瞬断会引起个别节点的DAF 出现较大值，但由于对应的静力位移值较小，因此，无需特别关注。总的来说，外环索瞬断会引起较中环和内环更显著的冲击效应。

图 14 不同重环索瞬断后屋盖结构的位移响应及DAFs 比较Fig. 14 Displacements and DAFs comparison for sudden failure of cables in different loops

4.3 不同类型拉索瞬断的冲击效应

本文对比分析了外环索H31 和张弦索H41 瞬断后的动力位移响应，如图15 所示。外环索瞬断引起的屋盖跨中节点位移达到413 mm，会显著大于张弦索瞬断。由DAF 响应分布图可以看出，在东西向，外环索瞬断会导致位移较大的节点(跨中区域)的DAF 均大于2；而张弦索瞬断导致其绝对位移较大的节点区域(JH5 节点附近)的DAF 值均小于2。同理，在南北向，外环索同样会导致JS5附近节点的DAF 均大于2。因此，从屋盖跨中节点位移响应来说，外环索瞬断会引起较张弦索瞬断更为不利的冲击效应。

图 15 不同类型拉索瞬断后屋盖结构的位移响应及DAFs 比较Fig. 15 Displacements and DAFs comparison for sudden failure of different types cables

4.4 不同数量拉索瞬断的冲击效应

限于篇幅，本节仅分析比较有代表性的中环索和外环索和张弦索瞬断组合的影响，分析工况如表3 所示。图16 为不同工况拉索瞬断冲击下关键节点位移最大值。可以看出：1) 当拉索瞬断引起的变形分布规律较一致时，如工况1 和工况2，多根拉索同时瞬断(工况4)会引起位移响应会大于任一单根拉索失效，如图16(a)、图16(b)所示；2) 但是，当拉索瞬断引起的变形分布规律不一致时，如工况2 和工况3，多根拉索同时瞬断(工况5)并不会大于单根拉索瞬断(工况3)；3) 由于屋盖的复杂性，多根拉索同时瞬断的位移响应(如工况4、工况5)与相应单根拉索瞬断工况的线性叠加结果(工况6、工况7)并不完全一致。

表 3 多根拉索瞬断对比工况Table 3 Analysis cases of multi-cables failure

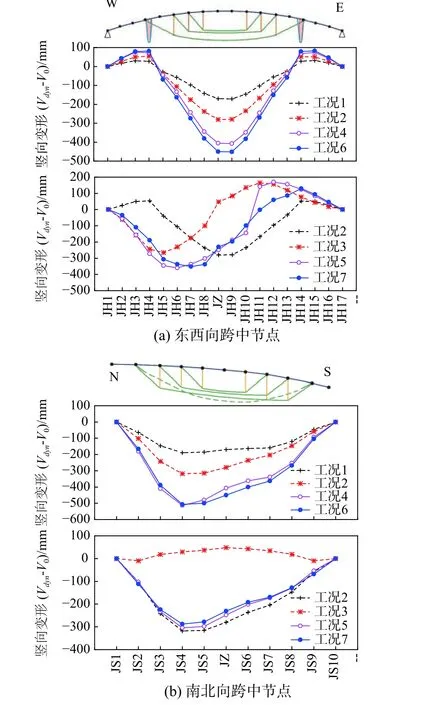
图 16 多根拉索瞬断后屋盖结构的位移响应及DAFs 比较Fig. 16 Displacements and DAFs comparison for sudden failure of different multi-cables

5 结论

本文针对多重环索-张弦穹顶屋盖的结构特点，探讨了断索冲击动力分析方法，并分析了多重环索-张弦穹顶屋盖的动力响应规律，主要结论如下：

(1) 针对多重环索-张弦组合屋盖，提出基于AP法的断索冲击动力分析方法，并开展动力分析参数的敏感性分析，研究结果表明：断索失效路径f(t)和断索持续时间t0均对断索冲击效应有较大的影响，而且两种参数对冲击效应的影响是相互的。因此，断索冲击动力分析时要特别注意此两个参数的确定。另外，结构阻尼比会影响结构断索冲击响应峰值和振动衰减时间；但是，屋盖初始荷载组合则对于弹性断索冲击效应没有影响。

(2) 多重环索-张弦组合屋盖的断索冲击动力响应结果表明：断索冲击作用下，剩余屋盖会产生十分显著的动力响应，响应峰值会显著大于拉索缓慢失效的静力响应。目前，规范[16−17]推荐的“DAF=2.0 的等效静力法”不仅无法准确反映断索冲击下动力响应的分布规律，而且DAF=2.0 的推荐值很大程度地低估了断索冲击放大效应。因此，对于此类复杂的穹支屋盖，建议使用基于AP 法的直接动力时程分析法进行断索冲击效应研究。

(3) 不同位置、类型、数量的拉索瞬断冲击效应分析表明：对于柔性撑杆的穹支屋盖，同一环中任一拉索瞬断的冲击效应是一致的；初始应力较大的外环索瞬断引起的冲击效应会大于中环和内环索；外环索和张弦索瞬断引起动力响应均较大，但分布规律差异较大。多根拉索瞬断的响应并非总是大于单根拉索瞬断。