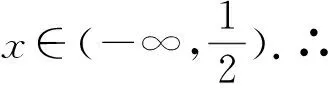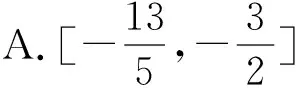对形如“存在x0，使得f(f(x0))=x0成立”问题的研究

四川省南充高级中学顺庆校区 (637000) 张小丹 李 婷

分析：对于初次遇到这道题的很多同学而言问题的难点是：对条件f(f(x0))=x0的变形处理.左边是“两层”函数，其实我们可以利用函数的单调性去掉一个“f”，再将之化为一个较为熟悉的问题，易于求解.

(2)再研究条件f(f(x0))=x0.若f(x0)x0，因为f(x)单增，∴f(f(x0))>f(x0)，与假设矛盾；故f(x0)=x0.

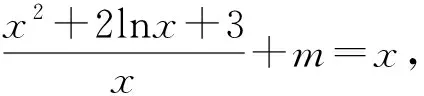
反思1：事实上我们不难发现，只要函数在给定区间上具有单调性，我们都可以如法炮制.

结论不妨设f(x)在所给区间D上是增函数，若存在x0∈D，使得f((x0))=x0，则问题等价于方程f(x)=x在区间D上有解.

证明：若f(x0)x0，因为f(x)单增，∴f(f(x0))>f(x0)，与假设矛盾；故有f(x0)=x0.

反思2:我们还可以将原题“存在x0”改为“存在2个x0”或者“存在唯一一个x0”，研究方法相同.

例1已知函数f(x)=ex-x-a，若∃x0∈[0，1]，使得f(f(x0))=x0，则a的取值范围是.

详解：f′(x)=ex-1≥0在区间[0,1]上恒成立，∴f(x)在[0,1]上单调递增.∴原问题等价于：方程f(x)=x在区间[0,1]有解.方程f(x)=x可化为ex-x-a=x⟺ex-2x=a2②.设g(x)=ex-2x,x∈[0,1]，∴问题②等价于函数g(x)的图像与直线y=a有交点，由g′(x)=ex-2，令g′(x)=0可得x=ln2，∴g(x)在[0,ln2]上递减，在[ln2,1]上递增，从而g(0)=1,g(ln2)=2-2ln2,g(1)=e-2

答案1.D；2.[1,e].