基于FPGA 的采样率转换滤波器联合仿真验证方法*

唐 衡，张 晶，赵 欢

(北京轩宇信息技术有限公司,北京 100089)

0 引言

数字滤波器是通过改变或者修正时域或频域中数字信号的属性，从输入的数字信号中提取有效的信号成分，来滤除不需要的信号成分或者干扰成分。数字滤波器在数字通信中使用非常频繁。在通信信号处理系统中，考虑计算量和存储空间要求，就需要不同的采样率间的相互转换，即多速率数字信号处理，包括使采样率升高的内插和使采样率降低的抽取两种方式[1]。而随着数字滤波器理论的成熟与半导体芯片产业的高速发展，FPGA 的大量使用使得数字滤波器的设计变得更加准确便利。

基于FPGA 的数字滤波器的大量应用，使得相应数字滤波器的验证技术也飞速发展。为了确认数字滤波器是否准确地实现了设计功能，就需要对数字滤波器进行验证。验证通常被认为是一种从根本上有别于设计的行为[2]。目前已存在的形式化验证工具需要专门化的知识，很难掌握，但是仿真验证是一种远比形式化验证更常采用的验证技术[3]。本文介绍常用的采样率转换滤波器CIC 滤波器和Farrow 滤波器的基本原理、FPGA 实现以及具体的验证方法，最后给出验证结果。

1 数字采样率转换滤波器概述

采样率转换 (SRC) 在通信中应用非常普遍，在通信系统中，输入采样率和输出采样率常为整数倍或分数倍的转换。目前，常用任意数字采样率转换结构，在整数倍时级联积分梳状滤波器（Cascaded integrator-comb，CIC）运用较多，而在分数倍时Farrow 结构滤波器[4]则更具优势。

1.1 级联积分梳状（CIC）滤波器

级联积分梳状（CIC）滤波器可以高效地实现抽取或者内插，尤其适用于软件无线电通信系统中处于高采样率的数字前端使用[5]。CIC 滤波器仅利用加法器、减法器和寄存器的特点，占用资源少，实现简单且速度快，所以非常适用工作在高采样率下。数字下变频（Digital Down Converter，DDC）中，CIC 滤波器起着重要的作用，它的主要功能是对采样速率的抽取，同时具有低通滤波器的特性。

抽取CIC 滤波器由一对或多对积分—梳状滤波器组成，输入信号依次经过积分、降采样以及与积分环节数目相同的梳状滤波器三部分，如图1 所示。

在内插CIC 中，输入信号依次经过梳状滤波器，升采样，以及与梳状数目相同的积分环节，如图2所示。

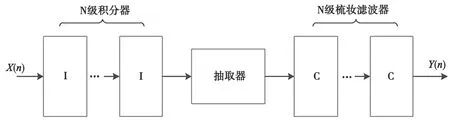
图1 抽取CIC 滤波器结构

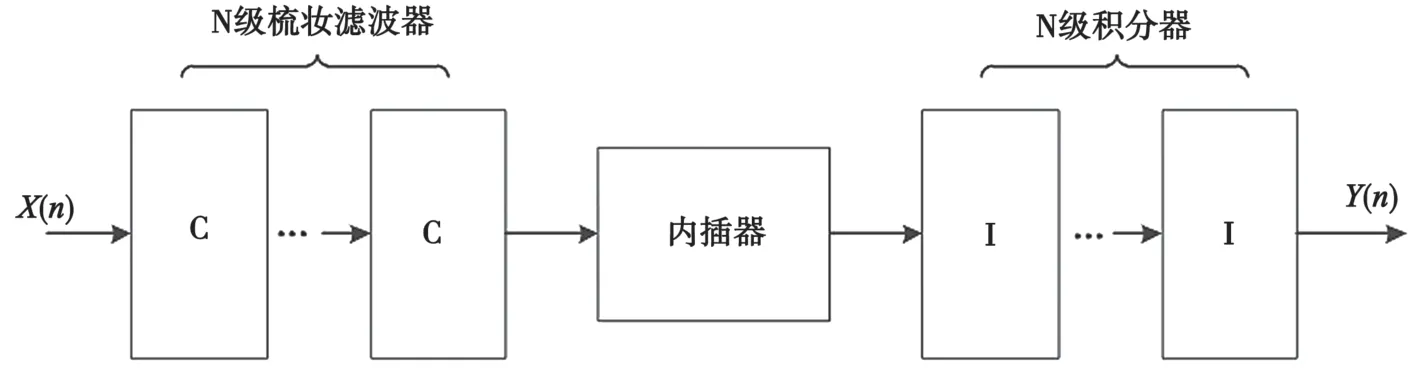
图2 内插CIC 滤波器结构

1.2 Farrow 滤波器

工程应用中不仅有整数采样率变换需求，同样有任意小数采样率转换的需求。内插估值的实现方法应运而生，它是基于数值分析的插值理论发展起来，其基本思想就是用原始的采样值构造插值函数，然后根据插值函数求出未知点上的信号值，并以此作为对真实值的逼近[6]。CIC 滤波器适合于整数倍插值或抽取，以及抽取和插值都比较小的分数倍数的采样率转换。Farrow 滤波器可以高效地实现任意因子(包括无理数)的采样率转换。

对于Farrow 结构的拉格朗日内插滤波器[7]，设输入信号周期为Tx，输出信号周期为Ty，转换公式如下：

对于任意因子的采样率转换，设mTy=(km+Δ)Tx，km为整数部分，Δ 为小数部分，则上式可转换并简化为：

用N阶多项式逼近h(k+Δ)，一般使用拉格朗日多项式，同时改变求和顺序，可得：

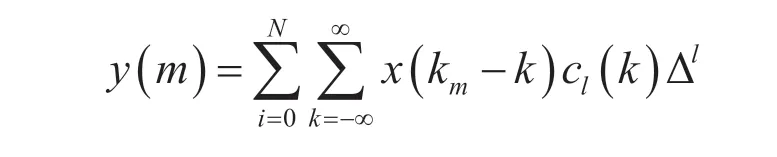
利用Horner 法则，可得出Farrow 滤波器的具体结构，M为滤波器阶数，N为拉格朗日插值的阶数。

如图3 所示：

图3 Farrow 滤波器结构

2 联合仿真及验证

仿真验证是一种最常见的动态验证方法，形象直观，实现简单，能够通过覆盖率检查测试验证的充分性。验证平台（testbench，简称tb）通过产生特定的测试激励，观测设计输出，通过比对结果判断设计的正确与否。对于复杂的信号处理算法类验证，可结合其他软件的接口，生成复杂的激励信号，同时将需要的数据存成文件，进行后续的自动比对，必要时结合其他分析工具进行进一步分析。在采样率转换滤波器的验证过程中，以SystemVerilog 为主要开发语言，选用IES 和MATLAB 软件进行多工具联合仿真，采用ModuleBase 的环境开发方法，能准确验证算法原型。

图4 联合仿真验证方法

3 内插滤波器验证结果及分析

按照验证流程对内插滤波器做了联合仿真验证和分析。

3.1 设计与环境搭建

FPGA 设计中，在确定了滤波器参数后，可以使用IP 核的方式实现设计，一个60MHz～240MHz的四倍内插滤波器的设计和接口如图5 和图6 所示：

图5 xillinx IES 中滤波器IP 核设置图

图6 IP 核接口

对图6 中IP 核设置的四倍内插滤波器rdss_inter_filter1 进行验证，使用SystemVerilog 语言在IES 中搭建仿真验证模型，主要完成的验证任务有：

（1）clk_mod 时钟生成，给DUT 主时钟和data_mod 的数据时钟；

（2）data_mod 数据生成，按照设置的频率连续给DUT 数据激励，并收集通过DUT 内插滤波之后的数据，得到仿真结果；

（3）MATLAB 联合仿真，将给DUT 的数据和通过DUT 内插滤波之后的数据输入MATLAB 做FFT 变换，得到辅助验证结果。

3.2 联合验证结果及分析

输入60MHz 为载波的激励波形r_da_data_test，得到内插之后的结果w_da_data_test。结果仿真波形如图7 和图8 所示。

图7 四倍内插滤波器滤波前后仿真图形对比

图8 四倍内插滤波器滤波前后数据对比

由仿真结果可知，四倍内插滤波周期从16.668ns 到4.168ns，即60MHz 到240MHz，与设计的四倍内插滤波相吻合。

由于IES 仿真验证中验证了滤波器的内插正确性，MATLAB 则作为辅助性的验证工具，验证滤波器的准确性。由于内插是提高采样率，通常会带来镜像干扰，需要确认结果中是否有镜像干扰。在MATLAB 中，随机截取一段四倍内插滤波前后的数据做FFT 变换，其结果如图9、图10 所示：

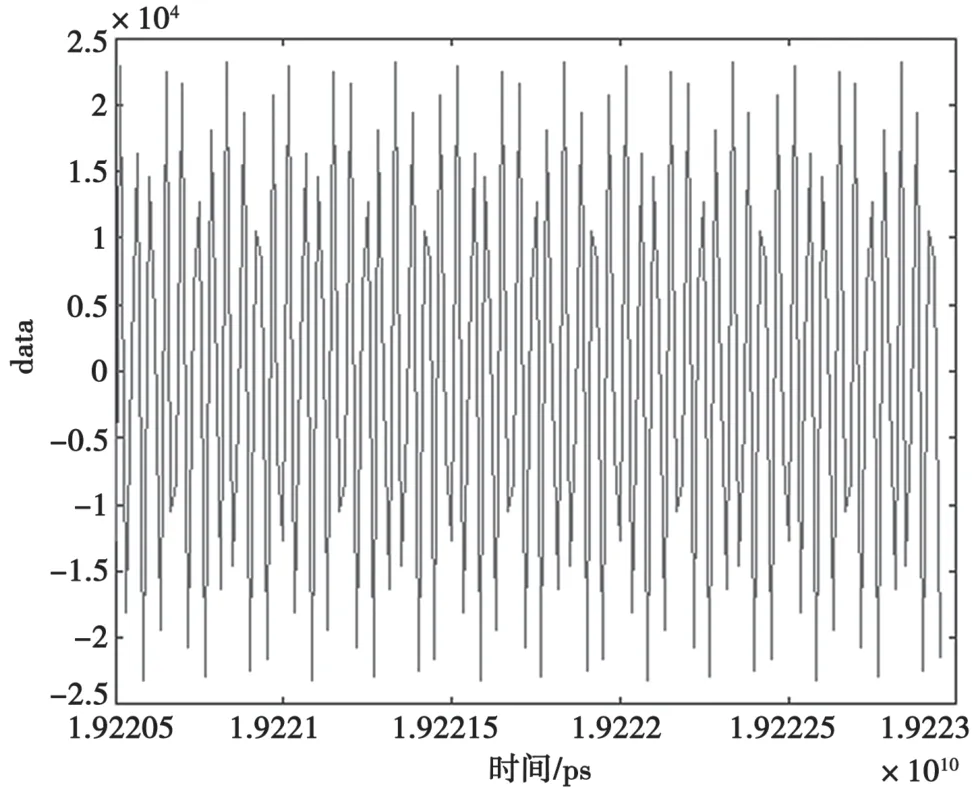
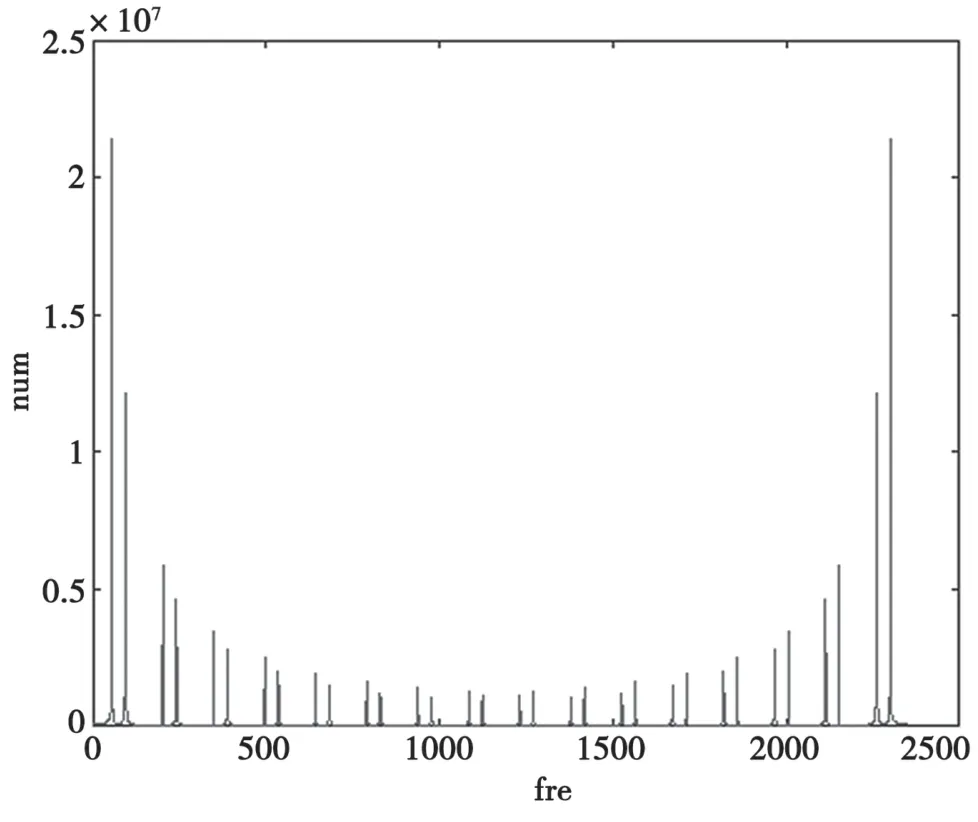
图9 内插滤波器滤波前数据截取与FFT 变换

由FFT 变换之后的结果可以看出，四倍内插滤波正确，而且也没有产生镜像结果，验证了设计的准确性。

4 Farrow 滤波器验证结果

按照验证流程对Farrow 滤波器进行联合仿真验证和分析。

4.1 设计与环境搭建

对于高灵敏度接收机，需要考虑码多普勒的影响，码多普勒成为一个捕获需要重点关注的因素。进行码多普勒补偿的可变分数阶延迟滤波器多采用Farrow 结构，具有码多普勒补偿模块的 GNSS 信号捕获框图如图11 所示[9]。

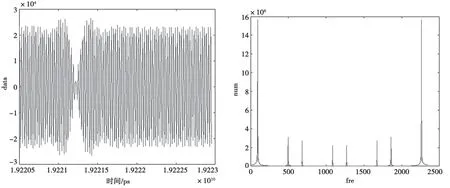
图10 四倍内插滤波后数据截取与FFT 变换

图11 具有码多普勒补偿模块的 GNSS 信号捕获框图

基于FPGA 设计Farrow 结构滤波器时，常采用MATLAB 的filterbuilder 滤波器设计工具箱，选择Fraction Delay 类型，按要求设置阶数后生成VHDL/Verilog 代码。

图12 滤波器接口

对图12 中伪码多普勒补偿部分进行验证，载波剥离后信号采样率为6.25MHz，伪码速率为6.138MHz，伪码多普勒为±264Hz。使用System Verilog 语言在IES 中搭建仿真验证模型，完成的验证任务主要有：

（1）clk_mod 时钟生成，给DUT 提供6.25MHz主时钟；

（2）data_mod 数据生成，向DUT 输入扩频信号（已完成载波剥离），伪码速率为6.138MHz，伪码多普勒分别设置为+264Hz 和-264Hz；

（3）MATLAB 联合仿真，将伪码多普勒补偿前后的数据输入MATLAB 进行FFT 变换，比对时域和频域信息，得到辅助验证结果。

4.2 联合验证结果及分析

以6.138MHz～264Hz 的码速率为例，IES 仿真结果如图13 所示。

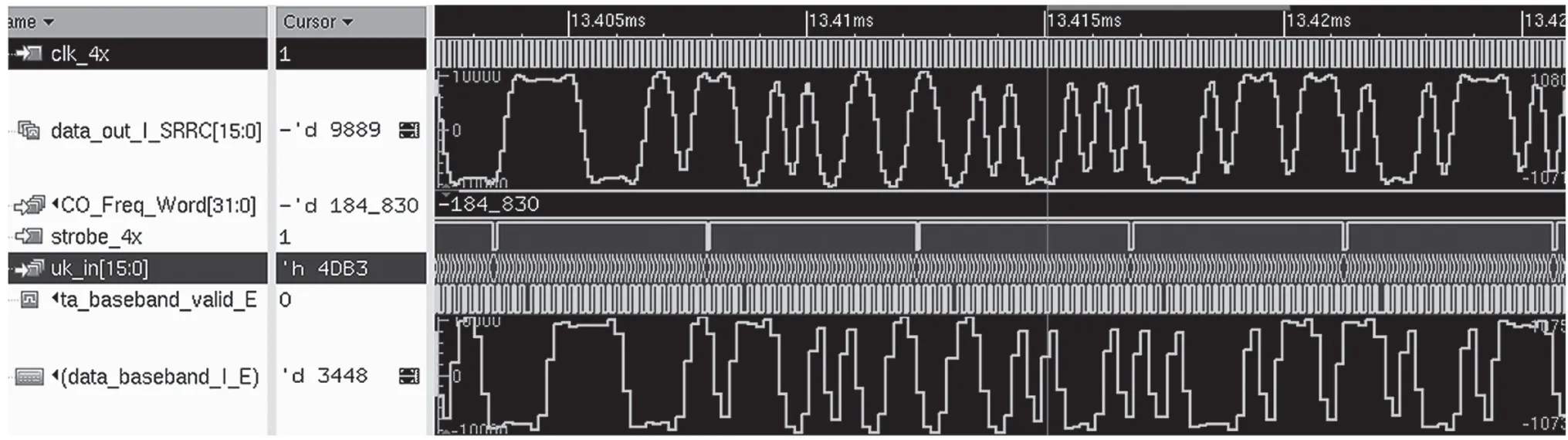
图13 采用Farrow 结构滤波器进行码多普勒补偿仿真

clk_4x 生成strobe 的NCO 量程为4373337504，频率控制字初始值为4294967296，多普勒偏移值为-184830，则实际保存至FIFO 的采样率为（4294967296-184830）/4373337504×6.25=6.137736MHz，与输入码速率一致。

采用MATLAB 进行FFT 变换，比对时域和频域信息，其结果如图14、图15 所示。

采样率转换前后时域和频域信息一致，验证了设计的准确性。

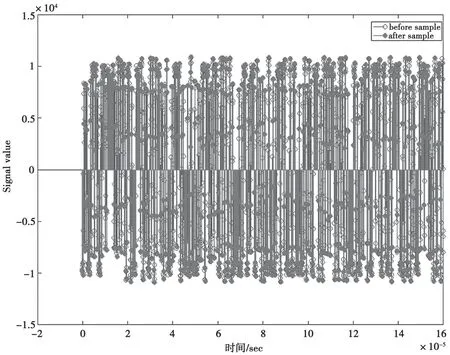
图14 采样率转换前后信号时域

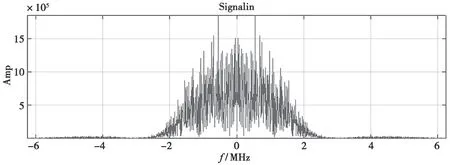
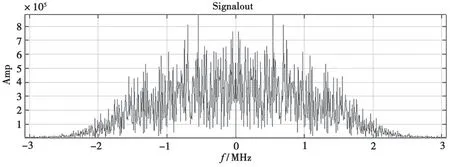
图15 采样率转换前后信号幅频特性

5 结语

本文给出利用MATLAB 和IES 实现的联合仿真实例，验证了基于FPGA 的数字采样率转换滤波器CIC 和Farrow 功能正确、性能良好，完全满足通用的通信信号处理系统中采样率转换要求。这种FPGA仿真平台结合多种EDA仿真工具的验证方法，降低了验证环境的复杂度，缩短了FPGA 设计及验证周期，增加了设计的准确性。与通用验证平台和针对特定FPGA 系统的验证技术相比，在验证效率和通用性等方面都具有不可比拟的优势。