吸盘式电磁铁残余吸力研究

宁剑建，章 晨，李 雨，李听斌，周奇慧，郑文鹏

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引 言

近年，随着我国航天事业的蓬勃发展，吸盘式电磁铁由于其结构简单、吸合力大、可靠性高、控制灵活方便，断电后自动释放等优点，广泛用于卫星载荷的锁定机构、航天器连接——释放机构，发挥重要作用[1-2]。但由于材料本身特性，电磁铁断电后会存在一定的残余吸力，影响连接——释放机构的正常释放动作。机构必须提供较大的驱动力，才可保证电磁铁和吸盘的分离，或增加弹簧等装置将电磁铁和吸盘分开，这导致了机构设计更加复杂，且降低了系统可靠性。本文结合某型号工程需求，分析了电磁铁断电残余吸力的机理和影响因素，在满足电磁铁通电吸力的前提下，提出了一种减小吸盘电磁铁断电残余吸力的方法，满足了工程应用要求。

1 吸盘式电磁铁结构原理

吸盘式电磁铁结构如图1所示，由电磁铁和吸盘两部分组成。其中电磁铁主要由环形线圈、线圈骨架和铁心构成，吸盘是由软磁材料根据接口要求设计加工的零件。

线圈通电产生磁场，吸盘与电磁铁之间产生吸力作用，吸盘与电磁铁吸合，断电后吸盘与电磁铁在外力作用下脱开。

由于电磁铁铁心和吸盘所用软磁材料并非理想材料，存在剩磁[3-4]，电磁铁即使断电，电磁铁与吸盘之间仍然存在吸力，在此称之为残余吸力，残余吸力大小取决于材料的特性。

图1 吸盘式电磁铁结构原理

2 电磁铁通电吸力与断电残余吸力原理分析

吸盘式电磁铁电磁吸力公式如下[5]：

(1)

式中：F为电磁吸力；B为接触面之间气隙的磁感应强度；S为吸合面有效面积；μ0为真空磁导率，μ0=4π×10-7H/m。

由此可见，电磁铁和吸盘之间的电磁吸力与接触面之间的磁感应强度B的平方成正比。为了便于分析，针对图1的电磁铁结构，建立通电状态的等效磁路模型，如图2所示。

图2 吸盘式电磁铁通电状态等效磁路图

根据等效磁路模型，可近似计算接触面之间的磁通和磁感应强度：

(2)

(3)

式中：Fc为电磁铁线圈磁动势；R1为电磁铁铁心内圈磁阻；R2电磁铁铁心外圈磁阻；R3为电磁铁吸盘磁阻；Rδ1为电磁铁铁心内圈与吸盘接触面气隙磁阻；Rδ2为电磁铁铁心外圈与吸盘接触面气隙磁阻；Φ为主磁路磁通。

当电磁铁断电时，考虑到软磁材料的磁滞特性，磁滞曲线如图3所示[6-7]，图2中的线圈磁动势Fc消失，但磁回路中仍然存在磁动势，可将电磁铁铁心和吸盘看成矫顽力(Hc)和剩磁(Br)较低的永磁材料[8]，等效磁路如图4所示。

图3 软磁材料的磁滞曲线

图4 吸盘式电磁铁断电状态等效磁路图

根据等效磁路模型，可近似计算接触面之间的磁通和磁感应强度：

(4)

(5)

图5 增加固有气隙的吸盘式电磁铁结构原理

3 设计仿真

针对上文分析，本文建立了电磁铁的通电断开状态有限元模型如图6、图7所示。断电状态的有限元模型与通电状态模型的不同之处在于断电状态线圈内安匝数为0，内铁心、外铁心和吸盘材料参数由软磁材料的直流磁化特性变为永磁材料的剩磁、矫顽力以及相对回复磁导率，磁化方向与通电状态主磁路磁化方向一致。电磁铁模型基本参数如表1所示。

图6 电磁铁通电有限元模型

图7 电磁铁断电有限元模型

表1 吸盘电磁铁模型基本参数

改变模型中固有气隙δ1的数值分别计算通电吸力和断电残余吸力，分别得到通电吸力和断电残余吸力随固有气隙δ1的变化关系如图8、图9所示，计算结果如表2所示。

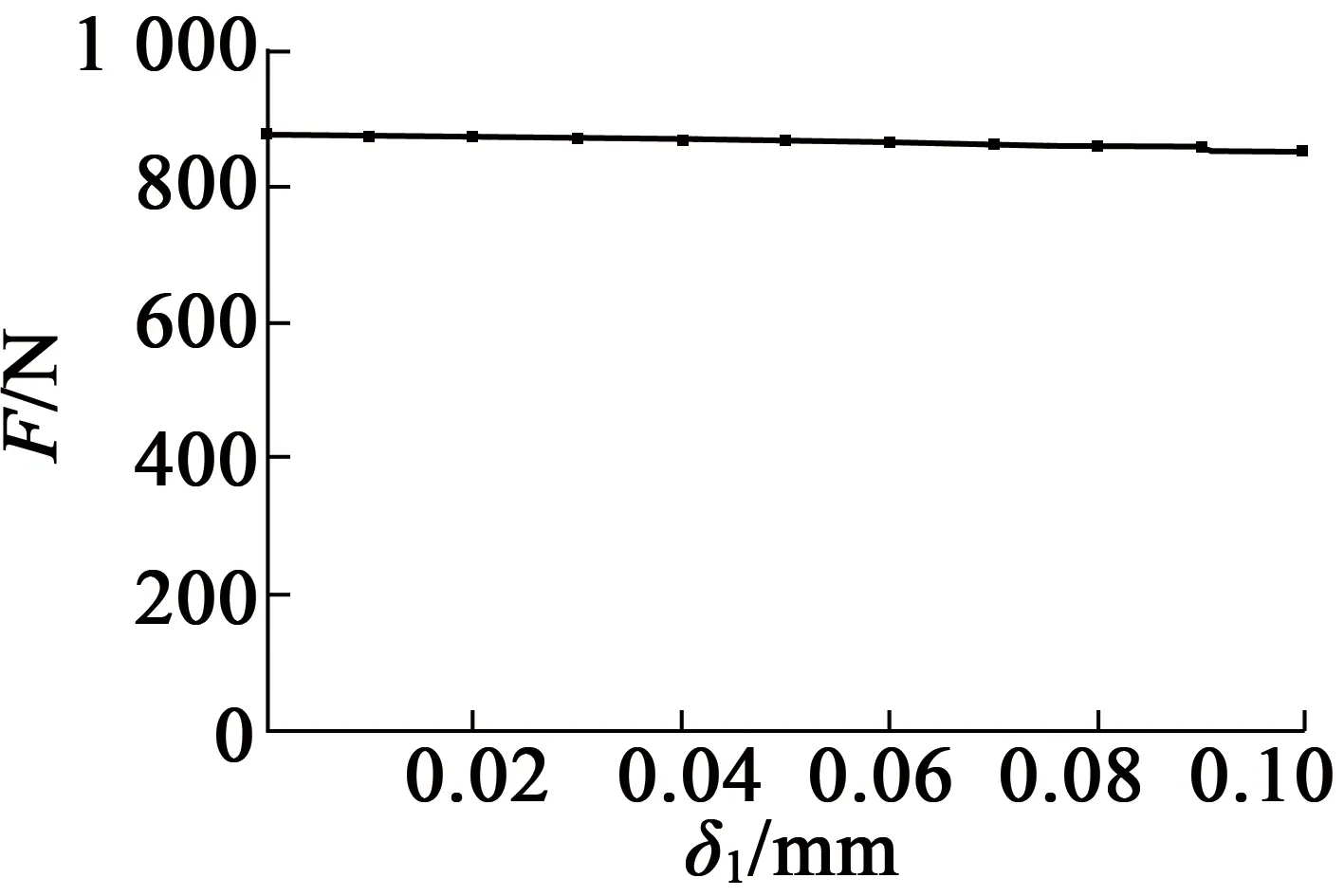
图8 电磁铁通电吸力随附加气隙的变化曲线

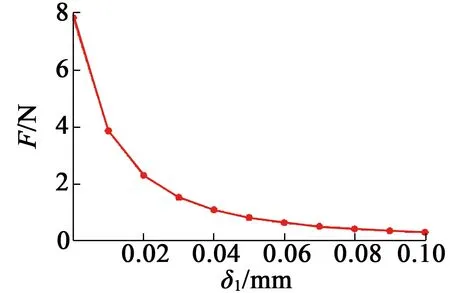
图9 电磁铁断电残余吸力随附加气隙的变化曲线

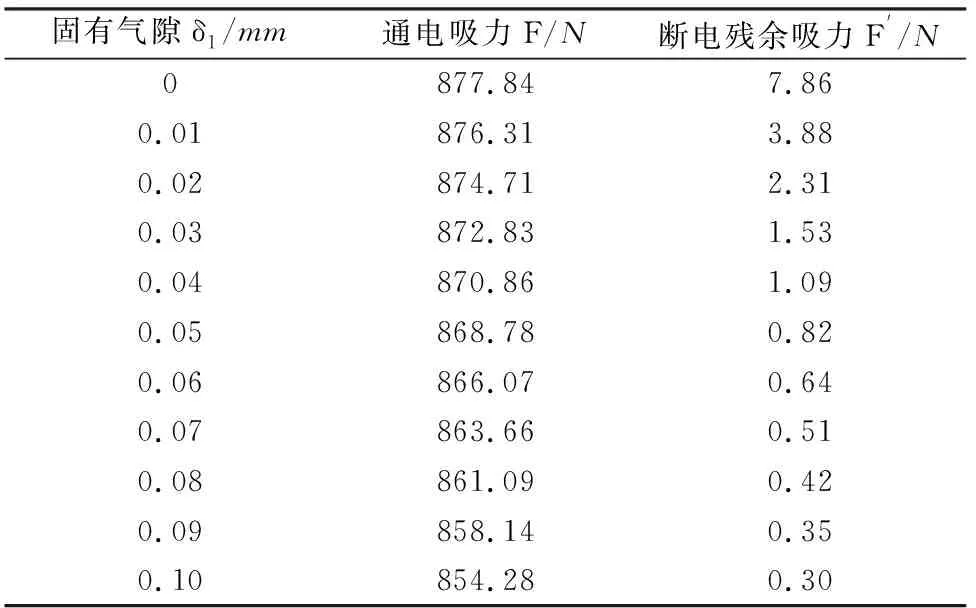
表2 通电吸力和断电残余吸力有限元计算结果

从表2中可以看出，当固有气隙δ1在0～0.1 mm范围内变化时，电磁铁通电吸力变化不大，而断电残余吸力迅速减小，与磁路分析所得结论一致。

4 样机实例

根据上述分析，研制了2台样机。1#样机电磁铁内外铁心平齐，2#样机电磁铁铁心内铁心比外铁心低0.04 mm。根据2台样机参数建立了有限元模型，计算结果如表3所示。

表3 样机模型的有限元计算结果

通过拉压力传感器对电磁铁通电吸力测试如图10所示，断电残余吸力通过吸盘下悬挂砝码的方式进行测试，如图11所示，测试结果如表4所示。

图10 电磁铁通电吸力测试

图11 电磁铁断电残余吸力测试

表4 样机测试结果

样机测试结果与有限元计算结果相差不大，同样证明了通过在铁心中增加固有气隙的方式可以在损失一小部分通电吸力的情况下，大大减小断电残余吸力。

5 结 语

吸盘式电磁铁由于材料本身的特性，存在断电残余吸力，在对断电释放有特殊要求的场合需要加以考虑。本文通过理论分析建立了电磁铁开通断电的磁路模型，分析了吸盘式电磁铁断电残余吸力的特性，提出了一种通过增加固有气隙的方式减小断电残余吸力的方法，有限元仿真计算和样机实测表明该方法简单有效。