单向预应力混凝土叠合板双向受力性能试验研究
2021-01-25刘慧颖主红香
刘慧颖 王 示,* 主红香 王 斌
(1.山东建筑大学土木工程学院,济南250101;2.山东乾元泽孚科技股份有限公司,济南250013;3.山东省交通规划设计院,济南250031)
0 引 言
近年来,装配式建筑在国内得到了广泛的应用[1],叠合板是装配式建筑中应用最多的配件,优势颇多的同时也存在很多问题,一直是业内关注的重点。叠合板的底板是在工厂按照规范标准统一预制,既作为上层现浇混凝土的模板来使用,也与上层混凝土共同承重,与现浇板相比,叠合板有节省工期与支模成本、施工简便及抗裂性好的特点,和预制板相比有较好的抗震性[2]。我国目前对混凝土叠合板的设计及应用主要分为两种情况:一种是预制部分是单向板,叠合后依旧按照单向板进行计;另一种是预制部分是尺寸较大的双向板,叠合后依旧是双向板[3]。单向配筋的预制底板有运输灵活、施工方便的特性[4-6],但叠合后板厚增加反而削弱了装配式建筑的优势;而双向配筋的预制底板则存在运输艰难、工业化效果差等问题。
1 ZDB 预应力混凝土叠合板的受力效应
ZDB预应力混凝土叠合板是由带桁架预制底板和现浇混凝土叠合层组成的楼板,其预制底板部分由预应力混凝土底板和纵向桁架组成,如图1 所示,桁架下的孔洞可以横向穿插布置非预应力钢筋,然后再浇筑叠合层使叠合板具有双向受力特性[7]。ZDB 预应力混凝土叠合板预制底板采用高强度钢筋施加预应力,既节省钢材、降低板厚,和普通预制楼板相比标准化程度更高,又减少了现场张拉所需空间、时间及支撑和模板数量;且板间拼缝紧密,无需设置现浇带,预制底板的自然粗糙面也大大加强了楼板的整体性。在我国的建筑工程中ZDB 预应力混凝土叠合板的使用量逐年增加,应用范围也在逐渐扩大,取得了巨大的经济效益与社会效益。
随着建筑结构的跨度逐渐变大,建筑特性向轻型、重载的方向发展,预应力混凝土叠合板的需求逐年增大[8]。ZDB 预应力混凝土预制底板钢筋桁架下的孔洞可以横向穿插布置非预应力钢筋,然后再浇筑叠合层可以使叠合板具有双向受力特性[9]。本文将对这种单向预应力矩形叠合板的双向受力性能进行研究,并给出此矩形叠合板的单双向区分界限。
2 按弹性理论ZDB预应力混凝土叠合单双向板的分界
如图2 所示四边简支并承受竖向均布荷载q的ZDB 预应力混凝土叠合板[10],长、短跨方向的计算跨度分别为l2、l1,1-1截面如图3所示、2-2截面如图4所示。

图1 ZDB预应力混凝土叠合板Fig.1 ZDB prestressed concrete composite slab
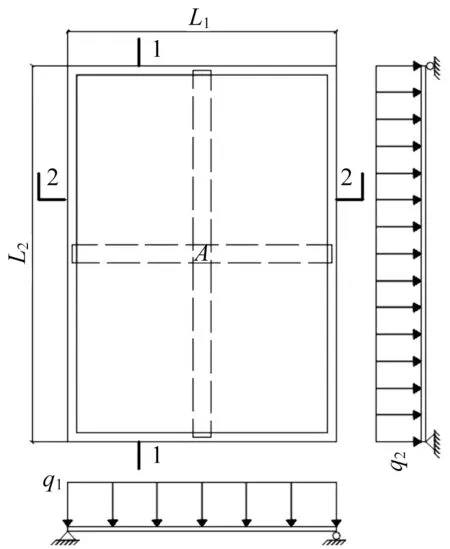
图2 四边简支的ZDB预应力混凝土叠合板Fig.2 ZDB prestressed concrete composite slab simply supported on four sides
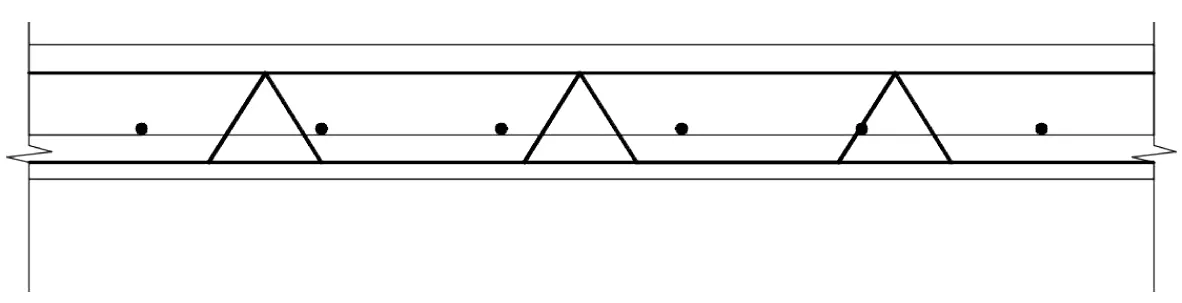
图3 1-1截面Fig.3 1-1 cross section
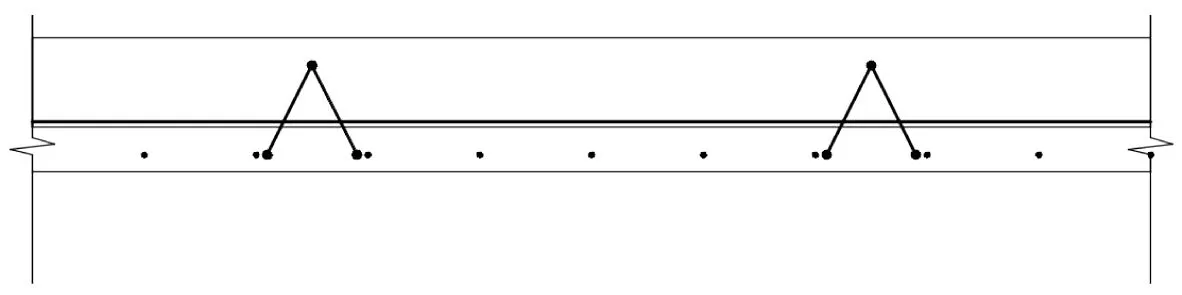
图4 2-2截面Fig.4 2-2 cross section
下面分析荷载q 沿长、短跨方向的荷载传递情况。取该矩形板形心A 处互相垂直的宽度为1的两个单元板带,假设沿长、短跨方向传递的荷载额分别为q2和q1,则q=q1+q2。根据弹性理论,当忽略相邻板带对它们的影响时,这两条板带就如同简支梁,那么由A点挠度相等的条件得:
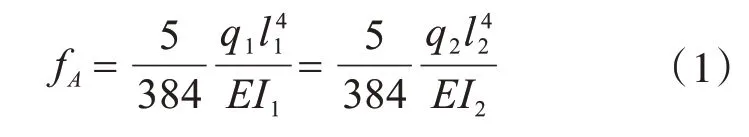
令


式中:h01p、h02p、h01d、h02d为普通钢筋混凝土板的截面有效高度、矩形叠合板的截面有效高度;η1p、η2p、η1d、η2d为普通钢筋混凝土板短、长跨方向荷载分配系数、矩形叠合板短、长跨方向荷载分配系数;μp、μd为普通钢筋混凝土板、矩形叠合板的长跨弯矩分配系数。
由上述方法计算的M2未考虑相邻板带的影响及与之垂直的短跨方向板带的支承作用,因此会偏大,实际的μ值应比计算值小[11-12]。对不同厚度的矩形叠合板进行计算和归纳,图4、图6 分别为预制底板板厚为40 mm、50 mm 时不同叠合层厚度矩形叠合板的μd和普通混凝土板的μp随长宽比变化的变化趋势,图5、图7 分别为预制底板板厚为40 mm、50 mm 时不同叠合层厚度矩形叠合板的η2d和普通混凝土板的η2p的变化趋势。观察曲线图可知,随着长宽比的增大,矩形叠合板和普通混凝土板的长跨荷载、弯矩分配系数都呈降低趋势;并且当预制底板厚度一定时,叠合层越厚矩形叠合板的长跨弯矩、荷载分配系数和普通混凝土板的越接近,叠合层的厚度对其影响较小。

图5 长宽比-μ曲线Fig.5 Length-width ratio-μ curve
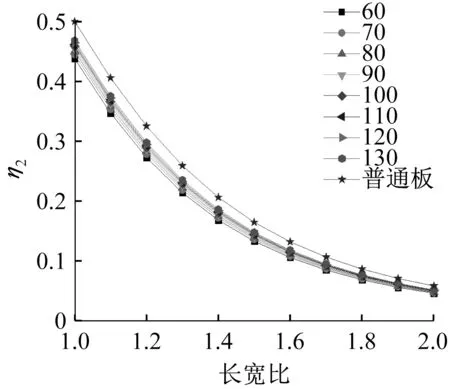
图6 长宽比-η2曲线Fig.6 Length-width ratio-η2 curve

图7 长宽比-μ曲线Fig.7 Length-width ratio-μ curve

图8 长宽比-η2曲线Fig.8 Length-width ratio-η2 curve
《混凝土结构设计规范》[13]规定:对四边支承的板,当长边与短边的长度之比小于2.0 时,宜按双向板计算,结合曲线图知当长宽比为2.0 时,普通混凝土板长跨弯矩占总弯矩的23.5%;预制底板厚40 mm时,长宽比不大于1.8时长跨弯矩占总弯矩的比例可达到23.5%;预制底板厚50 mm 时,长宽比不大于1.4 时长跨弯矩占总弯矩的比例均可达到23.5%。因此,当预制底板为40 mm 时,可以将l2∕l1=1.8作为矩形叠合板的单双向划分界限;预制底板为50 mm 时,可以将l2∕l1=1.4作为矩形叠合板的单双向划分界限。对曲线图进行分析,知叠合层厚度对弯矩分配系数的影响不大,矩形叠合板长跨弯矩分配系数随长宽比的变化可以归纳出一个系数α,其中α=μd/μp,具体数值见表1、表2。

表1 40 mm厚预制底板Table 1 Thickness of prefabricated floor as 40 mm

表2 50 mm厚预制底板Table 2 Thickness of prefabricated floor as 50 mm
3 试验研究
通过理论计算知由单向ZDB 预应力混凝土预制底板拼接的矩形叠合板板存在明显的双向受力效应,为验证上述结论并了解该矩形叠合板弹塑性阶段的受力性能,文章对四边简支ZDB 单向预应力混凝土叠合板进行了静力加载的破坏试验,对该矩形叠合板的受力性能、裂缝开展、破坏特征等进行了研究(试验材料的强度、弹性模量均采用名义值)。
3.1 试件设计
试验使用3块尺寸相同的ZDB 单向预应力混凝土预制底板,长度为3 000 mm,宽度为1 000 mm,厚度为40 mm。3 块预制底板均采用C40 等级混凝土,叠合层采用C30 等级混凝土浇筑80mm 厚。试件配筋表如表3 所示,配筋详图如图9-图12所示。

表3 预制底板配筋表Table 1 Reinforcement of prefabriciated floor

图9 预制底板配筋图Fig.9 Reinforcement of prefabricated floor
3.2 试件制作
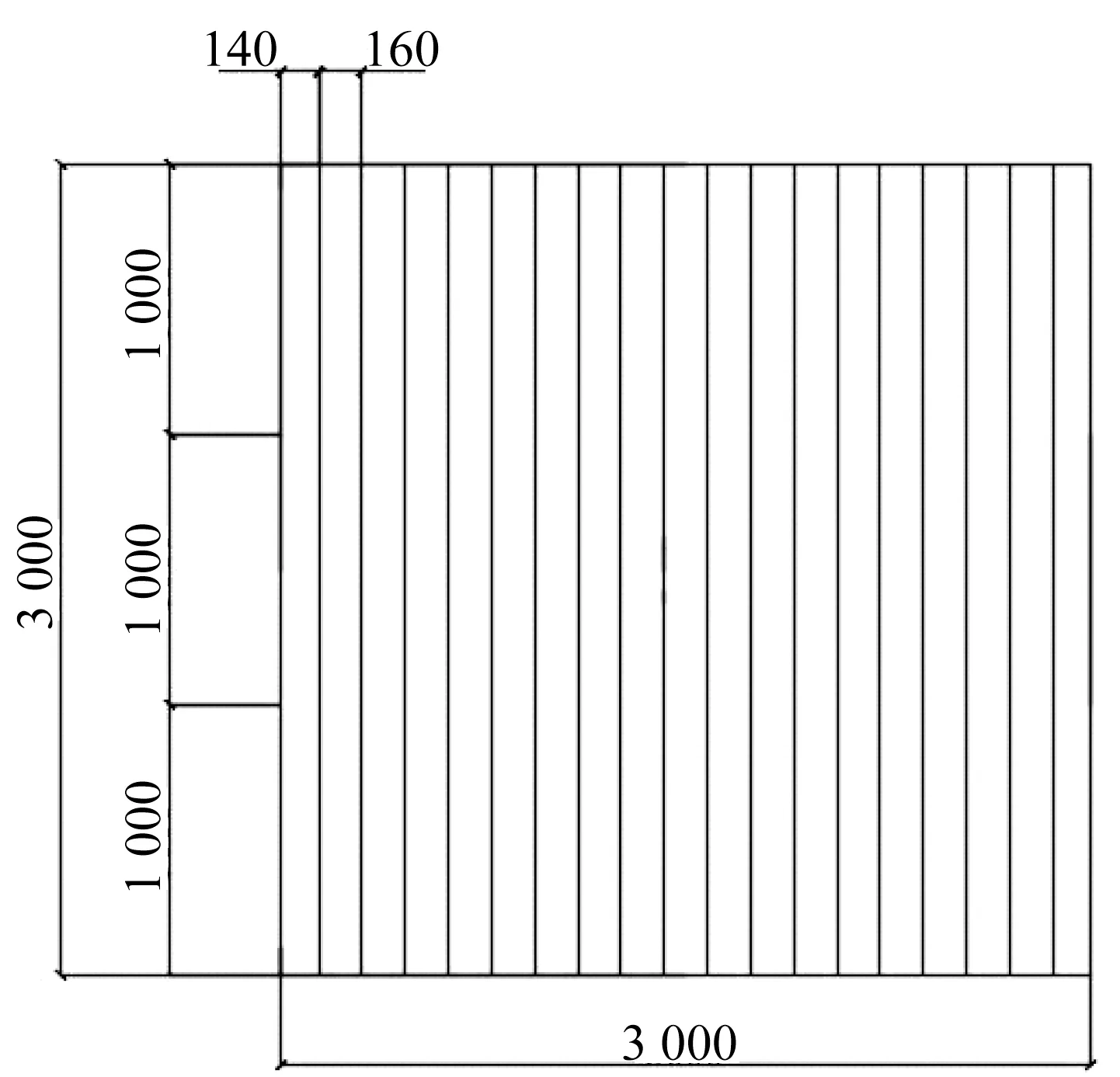
图10 叠合层配筋图Fig.10 Reinforcement of composite layer
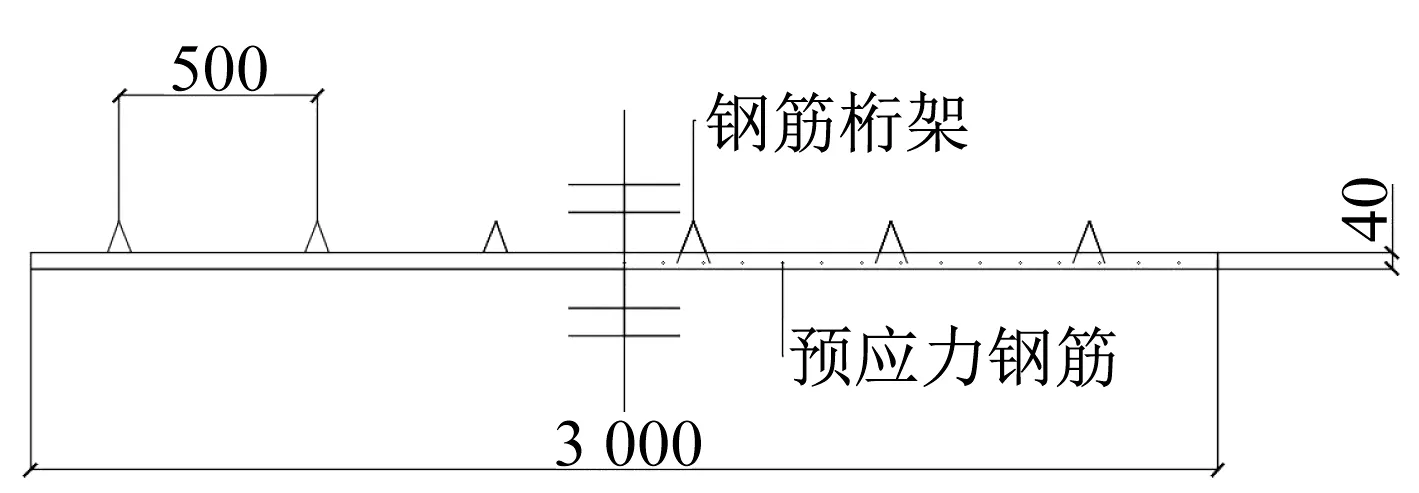
图11 预制底板配筋详图Fig.11 Reinforcement of prefabricated slab

图12 预制底板配筋详图Fig.12 Reinforcement of prefabricated slab
预制底板由长线法台座生产,制作时在预应力钢筋需要粘贴应变片的位置预留孔洞,如图13所示。同时为方便横向分布钢筋的绑扎并确保其位置固定,在矩形叠合板底板沿预应力钢筋方向的两侧各布置了两根钢绞线并绑扎固定,如图14所示。预制底板和叠合层浇筑时需分别预留同养护条件试块。

图13 底板预留孔洞Fig.13 Reserved hole in floor

图14 绑扎横向钢筋Fig.14 Transverse reinforcing bar
3.3 试验方法
此次试验的目的主要是验证拼接矩形叠合板的双向受力性能,需要观测预应力钢筋和横向钢筋的应力、叠合板的变形情况、开裂荷载和板底裂缝开展过程、叠合板的极限承载力。试验将叠合板简支在宽100 mm的钢支架上,为方便试验人员进出观测板底裂缝并采集数据,钢支架高度为1.5 m。为精确模拟四边简支同时减小楼板与支座之间的摩擦,在支架上方焊接了钢管作为铰支座,使楼板在支座处可以自由转动,如图15 所示。试验在矩形叠合板下表面跨中及支座处分别设置位移传感器;在混凝土下表面跨中设置混凝土应变片、在预应力钢筋和横向分布钢筋的跨中位置设置钢筋应变片,试验情况如图16-图21 所示。准备工作时期应先把矩形叠合板的底部用乳胶漆进行刷白,以便观测裂缝,并使用精度0.01 mm 的智能裂缝测宽仪对裂缝进行测宽;试验开始前分别测得预制底板和叠合层的同养护条件试块的混凝土强度等级为C40和C30。

图15 铰支座Fig.15 Hinged shoe

图16 试验现场图Fig.16 Test site

图17 试验加载图Fig.17 Test loading

图18 混凝土测点布置图Fig.18 Strain measuring point of concrete

图19 预应力钢筋应变测点布置图Fig.19 Strain measuring point of prestressing steel bars

图20 横向分布钢筋应变测点布置Fig.20 Strain measuring point of transverse reinforcing bars

图21 位移计布置图Fig.21 Displacement meter
试验采用沙袋堆积模拟均布荷载,首先将矩形叠合板划分区格,将各仪器读数调零后进行预加载,分三次逐级均匀加载,每次加载23 袋沙袋,每袋重30 kg,总重量为0.69 t,即0.77 kN∕m2。预加载过程中需检查各仪器是否正常运行,将所有仪器调试至精确后方可卸除荷载,再次进行正式加载。
4 试验结果与分析
4.1 试验现象及均布荷载-挠度曲线
由于试验所需荷载较大,考虑到安全问题,试验共准备500 袋沙袋,每袋30 kg,总重量为15 t。试验加载初期阶段,每级加载35 袋沙袋,即q=1.17 kN∕m2,每次持荷10 min。直至加载到385 袋沙袋时,此阶段的荷载作用下矩形叠合板的挠度、钢筋的应变都比较小,每级荷载下板跨中点挠度增量均约为0.3 mm,挠度、应变和荷载变化基本呈线性关系。
加载到420袋沙袋(q=14 kN∕m2)时,底板跨中预留孔洞边缘处出现2 条细微裂缝,裂缝宽度为0.04 mm。加载到455 袋沙袋(q=15.17 kN∕m2)时,预留孔洞边缘裂缝数量增加到5 条,最大裂缝宽度为0.06 mm,此级荷载下叠合板跨中点处挠度增量为0.55 mm,此时均布荷载-挠度曲线依旧可视为直线。
加载到500 袋沙袋(q=16.67 kN∕m2)时,矩形叠合板底跨中位置垂直于预应力钢筋方向出现3条裂缝,板的对角线处也出现了2 条长裂缝,其中最大裂缝宽度为0.09 mm。此级荷载作用下叠合板中点挠度迅速增加,增量为2.2 mm 且均布荷载-位移曲线在此时出现拐点,如图22所示。
试验后期每级在沙袋上方加载一个重量为2.16 t的预制楼梯,每级持荷30 min。随着后续的加载,矩形叠合板挠度不断增大,裂缝数量及长度不断增大并向对角线方向不断延伸。当加载了四个楼梯(q=26.27 kN∕m2)时,裂缝的发展已经非常充分,出现了典型的塑性铰特征,此时预应力钢筋和横向分布钢筋的应变均已进入了非线性阶段,最大裂缝宽度为1.54 mm,跨中总挠度为14 mm。根据承载能力极限荷载的判定方法,最大裂缝宽度大于1.5 cm 即达到承载能力极限状态,此时裂缝宽度1.54 mm>1.5 mm,故该矩形叠合板的极限荷载试验值为26.27 kN∕m2。此时已得到试验板的极限荷载,并考虑到实验人员的安全,中止试验,且试验板四边边界位置未出现明显上抬现象。
图22给出了在各级均布荷载下作用叠合板3个测点的挠度变化情况,其中测点1 是叠合板跨中挠度。根据实验数据,得到叠合矩形板垂直预应力方向开裂荷载为16.67 kN∕m2、极限荷载26.27 kN∕m2。矩形叠合板的极限位移与开裂位移之比为2.59,小于普通钢筋混凝土双向板的位移延性系数,主要是由于预应力提高了矩形叠合板的刚度并降低了它的变形性能[14]。本次试验得到的极限荷载为26.27 kN∕m2,已超出荷载设计值的2 倍,由此可得,由多块ZDB 单向预应力混凝土叠合板拼接成的矩形板具有较高的承载力且具有良好的抗裂能力。

图22 均布荷载-挠度曲线Fig.22 Load-deflection curve
4.2 预应力钢筋及横向分布钢筋应变
图23 、图24分别为预应力钢筋和横向分布钢筋部分测点的均布荷载-应变曲线,预应力钢筋的应变曲线不包含预应力初始张拉应变。由图可见,两条的曲线形状及变化规律和均布荷载-挠度曲线基本相似,加载初期两种钢筋的应变均呈线性变化且增长较为平稳,当均布荷载达到16.67 kN∕m2时,矩形叠合板底面在垂直于预应力钢筋方向和对角线方向均开始出现裂缝,此时由于受拉区混凝土逐步退出工作从而使钢筋承担的拉力猛增,钢筋应变都随之发生突变。从两条曲线可以看出两个方向钢筋的应变十分协调,充分证明了双向作用的存在。
4.3 混凝土应变及裂缝发展分布
根据有效数据点绘出了叠合板跨中点的均布荷载-混凝土应变曲线,从图25 中可以看出预应力及横向钢筋两个方向的混凝土应变的发展十分协调,充分证明了双向作用的存在且作用效果比较明显。
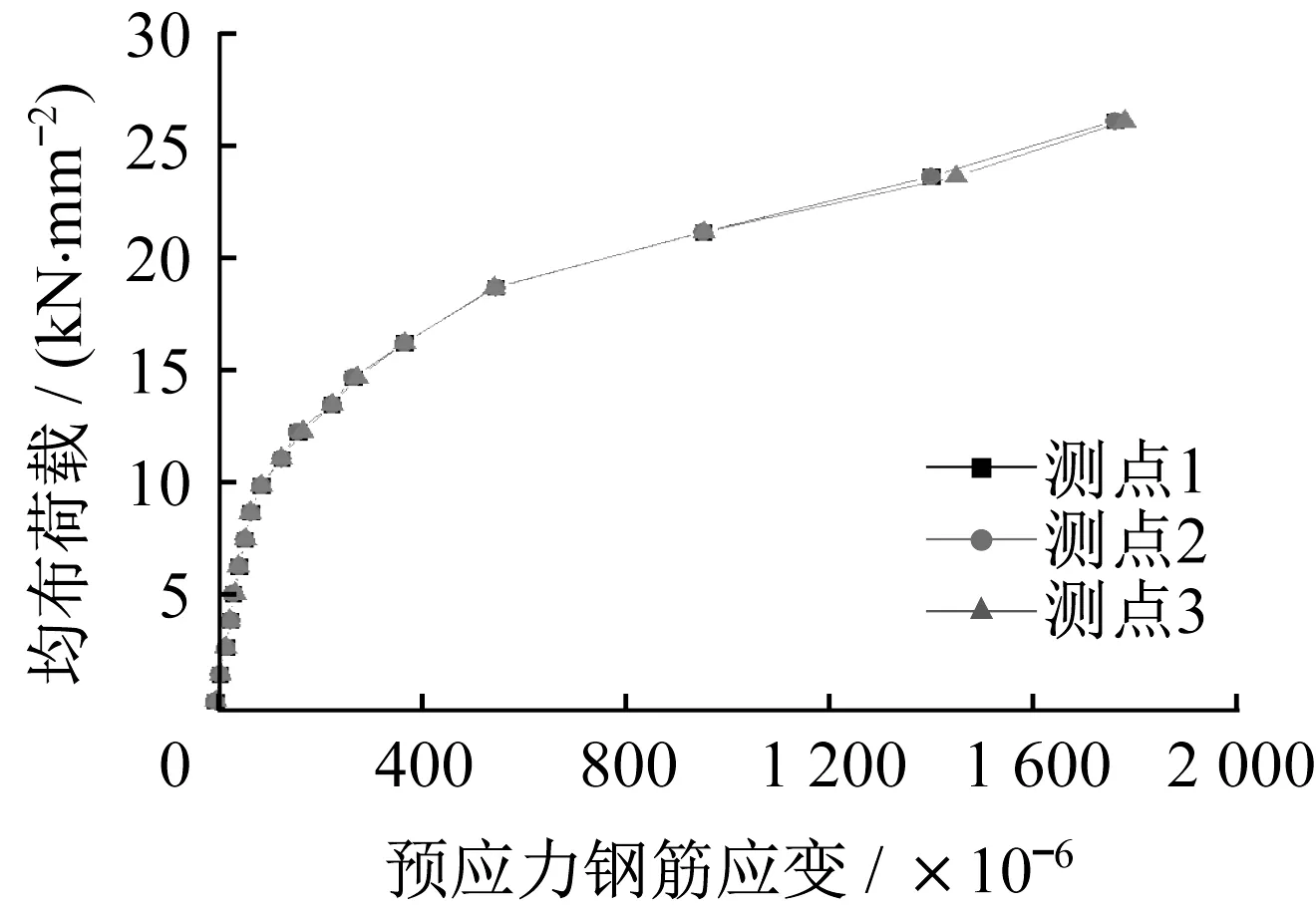
图23 均布荷载-预应力钢筋应变曲线Fig.23 Load-strain curve
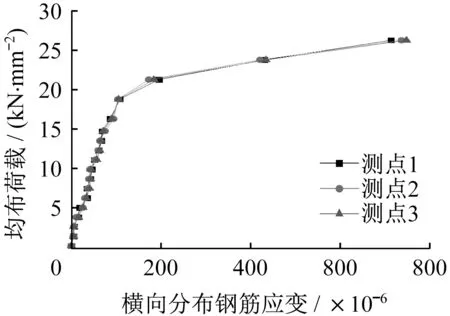
图24 均布荷载-横向分布钢筋应变曲线Fig.24 Load-strain curve
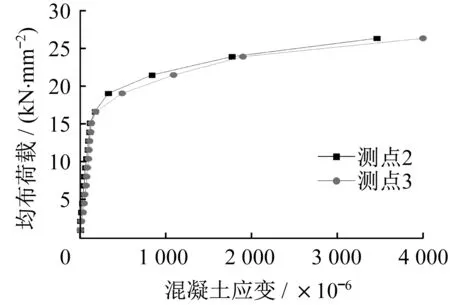
图25 均布荷载-混凝土应变曲线Fig.25 Load-Concrete Strain Curve
混凝土试验矩形叠合板裂缝如图26 所示(虚线为简化修正后的塑性铰线),根据裂缝分布图可以看出,四边简支的矩形叠合板和四边简支的普通双向板的裂缝分布、破坏形态十分相似。试验前期,矩形叠合板板底预留孔定的边缘处先出现了部分细微裂缝,此时混凝土、钢筋应变及挠度均无明显突变,直至试验荷载达到16.67 kN∕m2时,在跨中垂直于预应力钢筋方向出现了3 条裂缝、板底斜角方向出现了2 条裂缝,矩形叠合板在此级荷载作用下从未开裂状态进入到带裂缝工作状态,此时的荷载远超过了普通混凝土双向板的开裂荷载,所以斜向裂缝紧接着产生并开展,随着荷载的不断增大,板底裂缝向两端快速加宽并延伸,最后形成了塑性铰形态的裂缝分布状态。
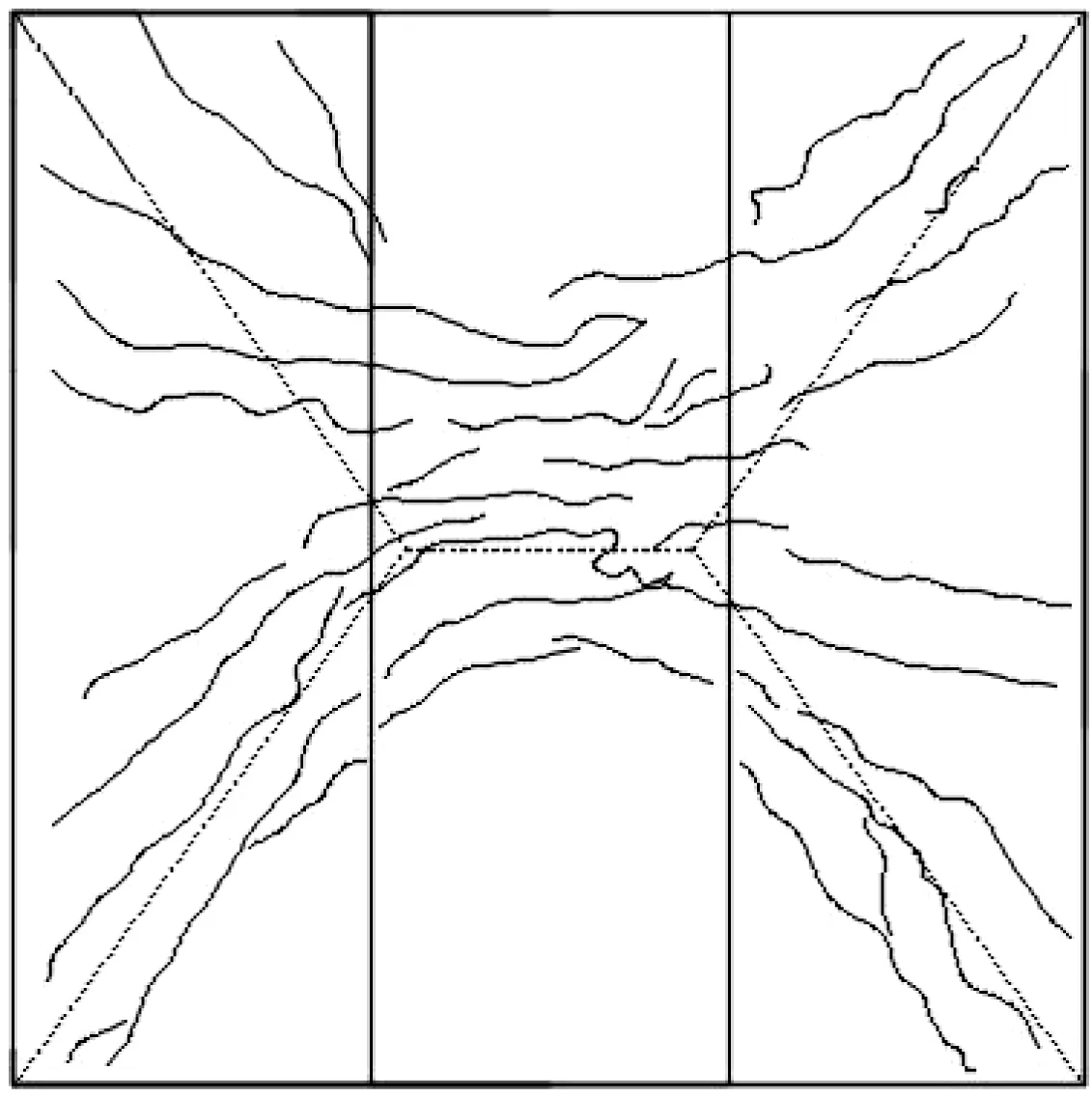
图26 叠合板板底裂缝分布图Fig.26 Fracture distribution in composite plate
4.4 弯矩试验值与计算值对比
以荷载q=10.5 kN∕m2时的弯矩为例对矩形叠合板的弯矩试验值和计算值进行比较。
根据《混凝土结构设计规范》(GB 50010—2010)[10],得
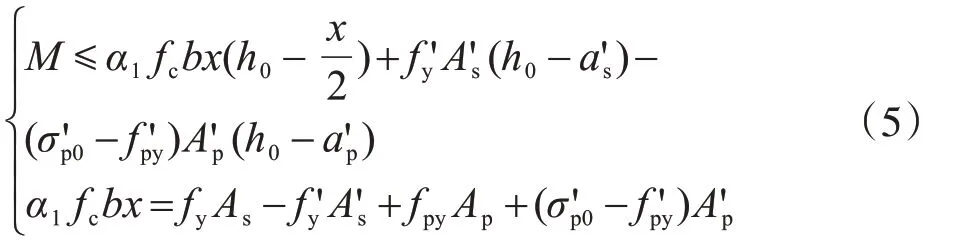
弯矩计算值:试验所用矩形叠合板长宽比为1.0,查阅双向板计算系数表得当长宽比为1.0 时,四边简支的双向板两个方向的分配系数均为0.036 8;根据表1可得,当矩形叠合板长宽比为1且预制底板厚40 mm时,α=0.910,故矩形叠合板平行于横向钢筋方向的分配系数为α·0.036 8=0.033 5,因此,M2计算=0.0335ql2=9.497 kN·m。
弯矩试验值:查阅试验记录数据,当荷载q=10.5 kN∕m2时,预应力钢筋应变ε1=103.4×10-6,横向分布钢筋应变ε2=45.5×10-6,叠合板有效截面高度h01=102.6 mm,h02=76 mm,计算得M2试验=9.511 kN·m。
分析得两个弯矩值的误差为1.37%,吻合程度较好。
4.5 极限荷载
试验所用矩形叠合板两个方向跨度相等:
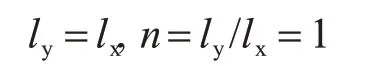
预应力钢筋的屈服强度、有效截面高度、内力臂系数、预应力方向每米内钢筋面积、沿预应力方向x单位板宽的极限弯矩为
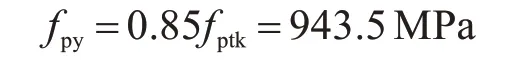

横向分布钢筋的屈服强度、有效截面高度、内力臂系数、垂直预应力方向每米内钢筋面积、沿垂直预应力方向y单位板宽的极限弯矩为

两方向跨中极限弯矩比值、塑性绞线长度比值为
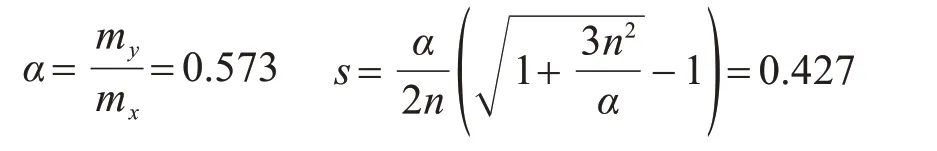
极限荷载为

由计算可得由ZDB单向预应力混凝土叠合板拼接成的矩形叠合板的极限荷载为29.57 kN∕m2,试验得到的叠合矩形板极限荷载为26.27 kN∕m2,两个的数值误差为11.1%。由于计算模型是基于塑性饺线极限模型,得到的结果为矩形叠合板极限荷载的上限,故两个数值的吻合程度相对较好。
5 结 论
通过对在多块ZDB 单向预应力混凝土预制底板拼接成矩形板的钢筋桁架下方穿插非预应力钢筋,从而实现双向配筋的矩形叠合板进行理论计算和静力试验,得到以下结论。
(1)矩形叠合板的挠度和应力分布都呈现了明显的双向受力特征,并且板的裂缝开展和破坏形态具有明显的塑性铰特征,说明了矩形叠合板的双向受力性能良好,可以按双向板进行设计计算。
(2)矩形叠合板的预制底板厚40 mm 时,在长宽比不大于1.8的情况下可以按双向板计算;预制底板厚50 mm时,在长宽比不大于1.4的情况下可以按双向板计算。
(3)双向矩形叠合板的双向计算系数可以用普通混凝土双向板的双向计算系数乘以系数α来计算,按这种方法计算的弯矩计算值和试验值对比吻合程度较好。
