方溪水电站面板缺陷下库水位骤降面板坝渗透稳定性分析

张红萍

（江苏城市职业学院建筑工程学院，南通226006）

0 引 言

面板坝是一种施工方面，坝坡稳定性好的堆石坝坝型，我国2011 年竣工的233 m 高的水布垭是世界上最高的面板堆石坝，同时，超过100 m 的面板堆石坝也有10 多座，如天生桥一级，古洞口及柴石滩等［1］，面板堆石坝在建成运行后，面板表面会出现大小不一的表面裂纹或者穿透性裂纹［2-3］，这些裂纹会对面板堆石坝的渗流特性甚至是稳定性产生巨大的影响［4-5］，因此，对于面板堆石坝缺陷下的渗透稳定性研究十分重要，对于面板堆石坝的设计及运行具有重大意义。

对于面板堆石坝的缺陷渗流特性的研究，国内外许多学者展开了大量的研究，如：李炎隆等［6］基于等宽缝隙稳定流的运动规律，推导了面板接缝止水失效且面板产生裂缝情况下面板堆石坝的渗流公式对某面板堆石坝进行了计算；高俊等［7］利用渗流专业计算软件Seep3D 对青海省玉树县境内的澜沧江某面板堆石坝面板缺陷下的渗漏量及浸润线进行了数值模拟研究。但是以上研究未涉及库水位骤降下含缺陷面板堆石坝渗透稳定性分析，事实上，库水位骤降下缺陷面板后的水压会使得面板承受指向坝坡外的渗透力，从而加剧面板的破坏，造成灾难性的后果，岑威钧等［8］、孙丹［9］、李传奇等［10］根据试验提出了“渗透系数扩大法”来模拟缺陷单元的渗透特性，取得了良好的效果，且计算简便，计算代价较小。

本文利用现有成果，基于“等效渗透系数扩大法”，对方溪水电站含不同缺陷下的面板堆石坝在库水位骤降下的渗透稳定特性进行了数值模拟，以期为该面板坝的运行安全稳定提供了一定的参考。

1 计算原理

1.1 非饱和渗流方程

非饱和渗流的控制方程形式为

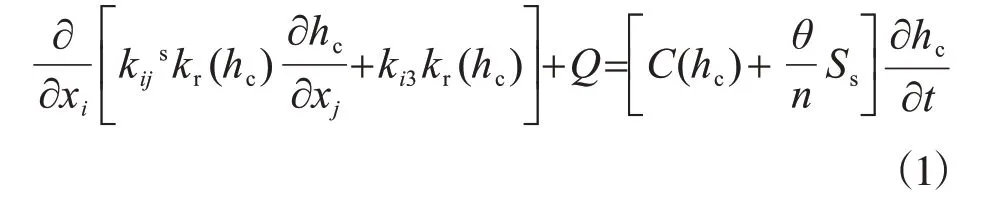
式中：kr为相对透水率；kij为饱和渗透张量；hc为压力水头；Q 为源汇；C（hc）为容水度；θ 为压力水头函数；n为孔隙率；Ss为单位贮水量。

1.2 面板单元的有限元模拟

由于面板的厚度远小于坝体单元的平均尺寸，有限元模型难以建立，文献［8-10］介绍了面板有限单元的建立，即根据等效原则，要求面板在厚度方向上满足：

同样，在面板的平面内，有

式中：kʹyʹ为土工膜平面内的等效渗透系数；kyʹ为土工膜平面内的渗透系数。

在进行有限元计算的时候，需要将局部坐标系转换为整体坐标系，转换公式如下：

本文将面板厚度放大100 倍，即面板厚度取为10 m处理。

1.3 缺陷面板单元的模拟

缺陷单元的模拟方法主要有两种：剔除单元法与渗透系数放大法［11］。剔除单元法是将缺陷处的面板单元剔除，然后在相应的位置施加相应的水头，这种方法能够准确地模拟缺陷面板的渗流行为，但是操作繁琐；渗透系数放大法是将缺陷面板单元赋予一个较大的渗透系数，建模方便，根据文献［11］的研究，只要将缺陷面板单元设置为强透水即可满足要求。

1.4 非饱和边坡抗滑稳定理论

非饱和边坡抗滑稳定理论如下所示：

在面板堆石坝有限元分析时，考虑非饱和状态对应含水量下的抗剪强度，可近似等效一种非饱和边坡抗滑稳定计算。

非饱和抗剪强度计算如下：

2 计算模型

方溪水电站堆石坝位于浙江省临海市境内，该水库任务是以供水为主，结合防洪，兼顾灌溉、发电等综合利用。坝址以上集水面积84.8 km2，多年平均径流量为1.08 亿m3，水库总库容7 205 万m3，正常库容6 101 万m3，供水调节库容5 898 万m3，防洪库容1 432 万m3，多年平均供水量6 776 m3，电站平均发电水头61.22 m，装机3 750 kW。拦河坝坝型为混凝土面板堆石坝，坝顶高程121.0 m，防浪墙顶高程122.2 m，坝基趾板底高程43.0 m，最大坝高78 m，坝顶宽度8.0 m，坝轴线长370.2 m。为计算方便，以图示坐标轴为基准，正常蓄水位为40 m，死水位为10 m，下游水位取为6 m，取如图1所示的剖面建立有限元模型，根据长年观测资料及建模方便，取如图所示的上部缺陷、中上部缺陷、中下部缺陷及下部缺陷四个部位缺陷进行分析，为提高计算精度，对全局网格进行加密处理，模型共划分为28 853个节点，29 031个单元。

边界条件如下：①bcd为库水位骤降边界，从40 m 骤降至10 m；②gh 为下游6 m 静库水位边界；③def，baih为不透水边界。

图1 计算模型及模型网格Fig.1 Computational model and model grid

3 材料参数

面板堆石坝不同分区的材料参数根据现场观测及室内试验综合确定，见表1，材料的非饱和土水特征曲线见图2。

表1 坝体材料力学参数Table 1 Mechanical parameters of dam materials

图2 土水特征曲线Fig.2 Soil-water characteristic curve

4 计算工况

为研究不同缺陷部位及缺陷尺寸下库水位骤降面板坝渗透稳定特性，对不同库水位速率联合不同缺陷下的面板坝渗流特性及稳定性进行了分析，相应工况见表2。

5 计算结果

5.1 浸润线变化

静库水位下不同缺陷高程及缺陷尺寸的坝体内部浸润线分布及库水位骤降下不同时刻浸润线的变化见图3、图4，其他静水位工况与缺陷高程为25 m 情况类似，限于篇幅，本文仅仅对完整面板坝及缺陷高程为25 m、缺陷尺寸为1 cm 情况下的不同时刻浸润线变化进行展示。

由图3可以看出：

（1）一旦面板出现缺陷，坝体的浸润线明显升高，这种变化在上游坝坡处较为明显，而在下游坝坡处变化不大，说明缺陷对于面板坝的渗流特性影响巨大。

（2）不同缺陷尺寸下（如图3 中缺陷高程为5 m，缺陷尺寸分别为1 cm、2 cm 以及3 cm）坝体内部浸润线的差别不大，但是总体上缺陷尺寸越大，坝体内部的浸润线高程也越高。

（3）相同情况下，缺陷高程越高，库水位高程越高，坝体内部的浸润线高程也就越高。

由图4可见：

（1）库水位骤降下，坝体内部浸润线随时间变化呈现“先疏后密”的规律，即在库水位骤降时坝体内部浸润线随时间变化较大，而在库水位骤降结束后浸润线随时间的变化较小。

表2 计算工况Table 2 Calculation cases

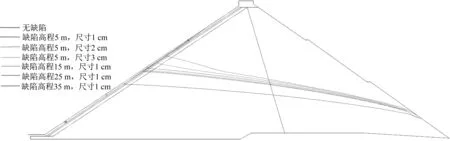
图3 初始静库水位（40 m）下不同工况浸润线变化Fig.3 Variation of infiltration line under different working conditions under initial static reservoir water level（40 m）

（2）含缺陷面板坝与完整面板坝相比，浸润线有一个明显的抬升，这可能对坝坡力学性能产生较大的影响。

（3）在库水位经过面板缺陷处的时候，浸润线有一个明显下降的过程。

5.2 坝体的渗漏量分析

不同工况下的初始稳态下坝体渗漏量柱状图见图5。

由图5可见：

（1）一旦面板发生缺陷，无论缺陷的位置尺寸如何，渗漏量将呈现一个明显的上升，以缺陷高程为5 m、缺陷尺寸为1 cm 为例，渗漏量较完整面板上升了68.2%。

（2）对于不同缺陷尺寸来说，缺陷尺寸越大，坝体内部的渗漏量越大，但是不同缺陷尺寸下的坝体内部的渗漏量变化不大。

（3）缺陷高程越大，坝体内部的渗漏量越大，渗漏量的变化幅值要大于缺陷尺寸不同引起的变化。

图4 完整面板与含缺陷面板在库水位骤降下浸润线变化Fig.4 Variation of soakage line between complete panel and defective panel under sudden drop of reservoir water level

图5 渗漏量柱状图Fig.5 Leakage histogram

5.3 库水位骤降下的坝体稳定性变化规律

不同工况下的上下游坝坡稳定性变化规律如图6所示。由图6可见：

（1）整体上看，上游坝坡安全系数随库水位下降呈现“先降后升”的趋势，下降呈现迅速下降的规律，而上升则呈现缓慢上升最后维持不变的规律；下游坝坡则呈现一直上升的规律，在库水位骤降前期上升较快，而在库水位骤降后期上升较慢最后维持稳定。

（2）库水位骤降速率越大，相同情况下的上游坝坡最小安全系数出现得越早，最小安全系数也越小；而下游坝坡安全系数上升得越快。

（3）一旦面板发生缺陷，安全系数较完整面板来说有一个较大幅度的下降，对于面板缺陷尺寸越大，安全系数整体上越小，但是不同缺陷尺寸下的安全系数差异不大。

6 结 论

（1）含缺陷面板会导致坝体浸润线明显升高，缺陷尺寸越大，缺陷高程越高，浸润线高程越高。

（2）库水位骤降时，坝体内部浸润线变化较大，呈“先疏后密”的规律，含缺陷面板浸润线大于完整面板。

（3）缺陷尺寸越大，缺陷高程越大，坝体内部的渗漏量越大，当含缺陷面板缺陷高程为5 m，缺陷尺寸为1 cm 时，其渗漏量较完整面板上升68.2%。

（4）上游坝坡安全系数随库水位下降呈现“先降后升”的规律，下游坝坡则呈现一直上升的规律，不同缺陷尺寸下的安全系数差异不大。

图6 不同工况下上下游坝坡稳定性变化Fig.6 Variation of slope stability of upstream and downstream dams under different working conditions