温度对屋架作用的分析
2021-01-25张宪恩
张宪恩
(攀枝花攀钢集团设计研究院有限公司, 四川攀枝花 617023)
随着社会的发展,对大跨度厂房需求越来越迫切。对大跨度空间,传统的结构是网架拱。但网架拱的施工场地不允许有别的作业,这样,网架拱用于对现有煤场、原料厂改造就受到一定限制。经过对传统屋架改良,将单片屋架设成空间桁架式,在大跨度空间上也具有一定优势。由于屋架跨度达几百米,温度的影响不可忽略。现相关规范,只是给出了限制条件,并没有给出影响原理及影响程度。本文分析温度对特大跨度屋架作用,从理论上认识温度对大跨度屋架的影响,以使广泛使用空间巨型桁架结构。温度在屋架分布上可能有差异,本文仅考虑,温度在屋架上均匀分布的情况。
1 温度对钢构件的作用
根据热胀冷缩原理,任何材料在温度变化的条件下,其体积都要发生变化,或其三个方向的尺寸都要发生变化。对钢构件,轴线的尺寸远远大于截面的尺寸。由于截面的尺寸很小,温度变化影响较小。加之,截面方向无约束,对结构几乎无影响。因此,我们忽略了钢构件截面方向的温度影响。钢构件轴线方向尺寸较大,特别是大跨度达几百米时,温度变化的影响不可忽略。钢构件的线膨胀系数记为α(对于钢材α=1.2×10-5/℃),那么,无约束的钢构件在温差为c,长度为l的变化长度为:
Δl=αlc
(1)
式中:Δl为钢构件长度变化量mm;α为钢材的线膨胀系数1.2×10-5/℃;l为钢构件的长度mm;c温差℃。
当钢构件两端有约束时,钢构件就不能自由伸缩,它的温度变化引起的长度变化量就要受到约束的影响。当温度升高时,由于钢构件要膨胀,而约束限制膨胀,这样就要在钢构件中产生压力。若钢构件长细比很大(大于250),从理论上讲,该钢构件没有承载力。因此对这样的钢构件,温度再升高,它也不会产生压力。为了简化问题,我们下面讨论的对象是,钢构件是刚性杆。且假定两端约束刚度相同,记为K。在有约束的条件下,温度变化,钢构件的长度变化ΔlG、力F为:
(2)
(3)

其余符号同式(1)。
当钢构件两端约束刚度不同时,温度变化使钢构件的长度变化ΔlG1、力F1为:
(4)
(5)
式中:
K1、K2为钢构件两端的刚度N/mm。
如果这个约束是柱时,由于钢构件伸缩△lG,使柱在竖向力作用下产生一个弯矩MZ,其值为:
(6)
式中:P为柱顶荷载(kN),其余符号同前。
2 温度对屋架的作用
屋架种类较多,本文仅讨论梯屋架。屋架两端约束形式有三种:下承约束、上承约束、端承约束,见图1。
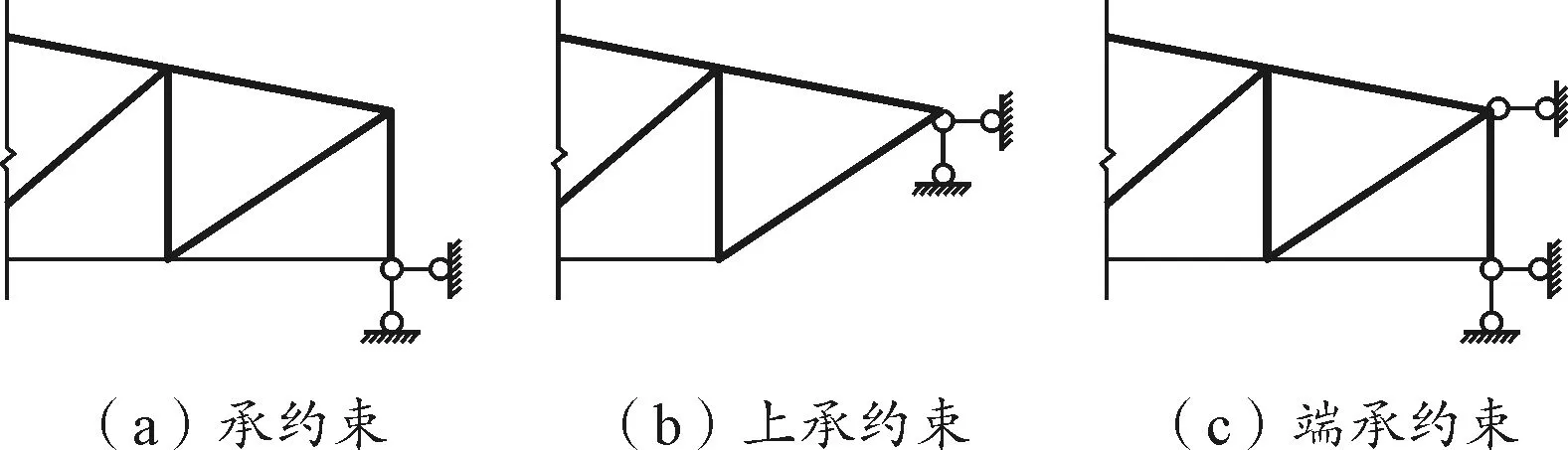
图1 屋架支座
屋架的端部也有三种形式:端杆为零杆、端杆为压杆、端杆为弹性杆,见图2。

图2 屋架端部结构
我们仅讨论前面两个形式,第三种形式工程中不多见,就不讨论了。
2.1 屋架两端无约束情况
屋架两端无约束的情况在工程中是没有的,我们只是从最简单的问题开始研究。梯形屋架一般是,上弦有5 %~20 %的坡度,下弦水平,中间有斜、竖腹杆。我们分析梯形屋架在温度作用下的变形形态。由于我们仅考虑构件在轴线方面的变形,未考虑构件横向变形。加上,梯形屋架在水平、竖的长度只有一个,虽然,上弦长了点,斜腹杆更长,但是在水平的投影与下弦长度是相同的。屋架的所有杆件材质是相同的。因此,梯形屋架在水平的伸缩量只有一个,那就是式(1)。梯形屋架在竖向的伸缩量也是梯形分布,端头小,中间大。在温度变化的过程中,并不在梯形屋架竖向产生内力。
2.2 屋架两端有约束情况
首先,我们讨论图1所示的情况。对于梯形屋架两端无约束的温度变化使其伸缩量见式(1),对于梯形屋架两端有约束的温度变化使其伸缩量是多少呢,下面讨论之。对于图1a所示的情况,当温度变化时,梯形屋架整体要伸缩,只有下弦有约束,那么影响温度影响的刚度是整个梯形屋架还是只是下弦杆件。所谓的刚度是,单位力作用产生的位移。让我们在屋架下弦两端加一个力F,见图3,根据力的平衡原理,只有下弦杆有力F。因此,对屋架两端有约束,温度变化的伸缩量同式(2),其钢杆件的刚度是梯形屋架下弦杆的轴拉压刚度。与端约束的作用力同式(3)。同样分析图1(b),也只是近似上弦杆水平刚度。分析图1(c),当端约束上下刚度相同时,也只是下弦杆、上弦杆水平刚度。
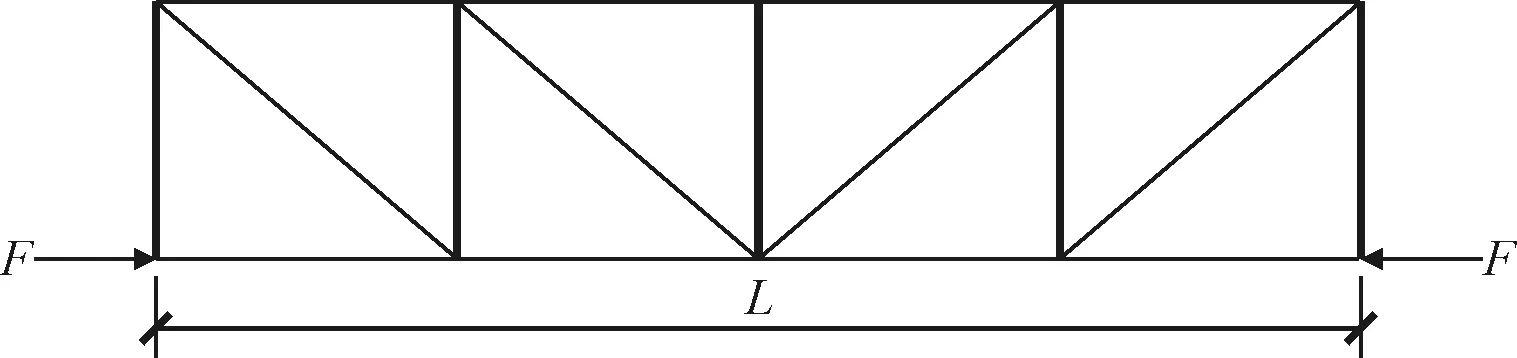
图3 屋架
上面讨论的对象是单跨厂房,下面讨论多跨厂房。多跨厂房柱顶标高相同,也可不同,只要相邻两屋架在同一柱上的标高是相同的就可以。屋架的长度就是跨度。假若有几跨,给柱编号,共有n+1个柱。以第一个柱为零点,向右为x轴正向。第i柱的水平位移记为△i,第i个柱的刚度记为Ki。第i个屋架的刚度、压力记为Kli、Fi。根据式(5)有:
(7)
作用在第i柱上的力有Fi,Fi+1,见图4,根据力的平衡,有下式:
Fi-1=KiΔi
(8)
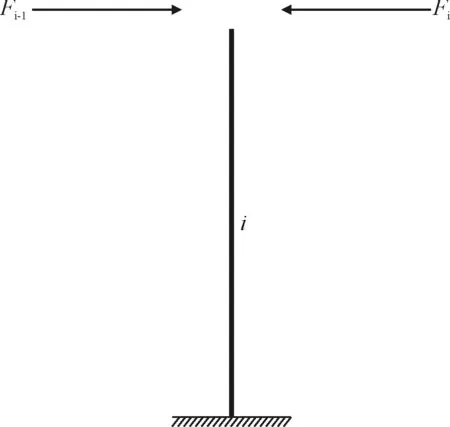
图4 第i柱受力
根据式(4),对第i个屋架,温度变化该屋架的伸缩量ΔlG1i为:
(9)
第i个屋架伸缩量与柱位移关系如下:
ΔlG1i=Δi+1-Δi
(10)
根据式(1),第i个屋架自由伸缩量Δli为:
Δli=αlic
(11)
第i个屋架自由伸缩量与约束量之间的关系为:
Δli-Δliy=Δi+1-Δi
(12)
(13)
整理式(7)至式(13),以Δi为未知数,建立一个n+1元一次非齐次方程组,求解,得到Δi,这样也就得到了Fi,ΔlG1i,也就得到了温度对多跨同高度屋架、及柱的影响。
再讨论高低跨的温度对屋架、柱的影响。所谓的高低跨,就是两相邻屋架在同一柱上的位置不同。高低跨与多跨的不同之处在于同一住上的位移不同,但有关系,见图(5)。式(8)改为:
Fii-1=Kii-1Δii-1
F1i=KiiΔii
(14)
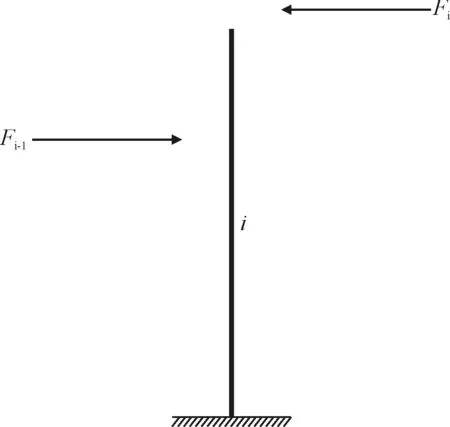
图5 第i柱高低跨受力
式中:Kii为第i柱在第i屋架处的刚度;Δii为第i柱在第i屋架处的位移。
(15)
式中:Kii-1为第i柱在第i-1屋架处刚度;Kiii-1为第i柱、第i-1屋架在第i屋架处产生的刚度;Kii-1i:第i柱、第i屋架在第i-1屋架处产生的刚度;其余符号同前。
式(7)、式(9),要用屋架与柱相应的刚度,式(10)改为:
ΔlG1i=Δi+1i-Δii
(16)
式(12)改为:
Δli-Δliy=Δi+1i-Δii
(17)
整理式(7)、式(9)、式(11)、式(13)~式(16),以Δii为未知数建立n+m+1元一次非齐次方程组(n:跨度;m:有高低跨柱子根数),求解这个方程组,得到Δii、Δii-1,从而得到Fi、ΔlG1i,也就得到了温度对高低跨的影响。
3 实例计算
某工程,屋架见图6,
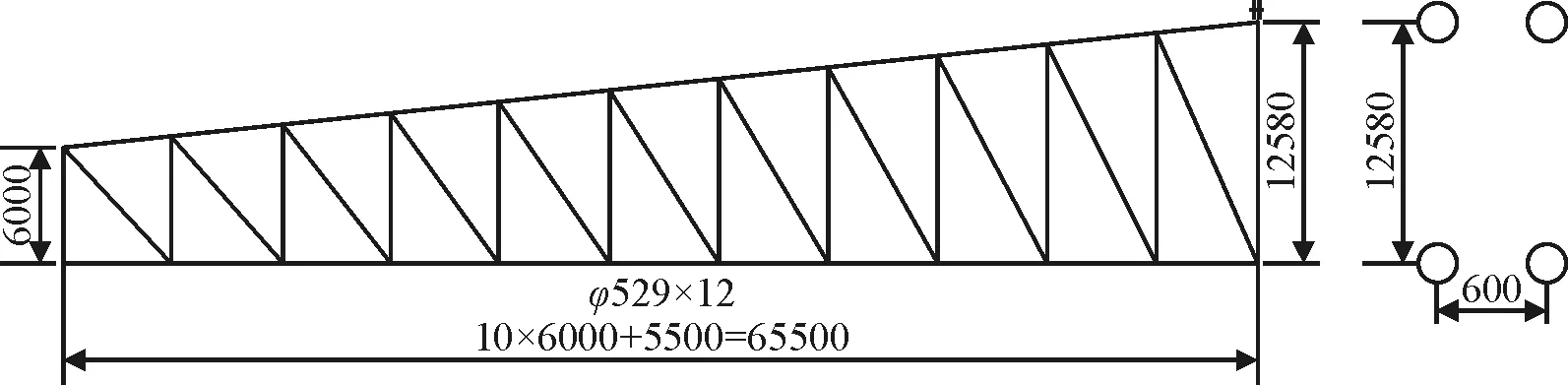
图6 屋架结构(单位:mm)
柱端刚度K=1.04×104N/mm。下弦杆的总面积:A=3.9×104mm2,钢材的弹性模量E=2.06×105N/mm2,屋架的刚度:
屋架两端约束的作用力F为:
由于屋架伸缩在柱中产生的弯矩MZ为(柱顶竖向反力为1 000kN):
MZ=34.6×1000=3.46×104N·m
4 结束语
经过对温度对屋架的分析及实例计算,温差在40 ℃时对屋架的影响占3.2 %,对柱的影响占27.2 %,即使当温度在20 ℃时,对柱的影响达13.6 %,因此,对大跨度的屋架结构,温度对柱的影响不可忽略。由于屋架伸缩使柱产生(P-Δ效应)弯矩占伸缩作用产生弯矩的0.46 %,因此,由于屋架伸缩在柱产生的弯矩(即P-Δ效应)可以忽略不计。
