三角形轻质复合屋架基本力学性能分析
2021-06-30杨军程杰
杨军 程杰
(西华大学,四川 成都 610039)
引言
当采用轻质复合材料接搭建三角形平面屋顶时,由于屋顶跨度的不同,屋架弦杆与腹杆的截面尺寸以及节间距会相应调整。对三角形钢屋架的杆件类型及立柱抗侧刚度因素对屋架的内力影响进行了研究。通过有限元数值分析方法对三个不同跨高比的单榀三角形豪威氏冷弯薄壁型钢屋架的受力机理进行了研究,得到三角形屋架的破坏模式为屋架整体屈曲破坏。由于三角形平面屋架以及节点构造的特殊性,需要检验典型跨度屋架的刚度、承载力、变形能力以及可能的破坏模式,屋架支座处的局部承压能力以及支座处的抗剪能力。从屋架选型、荷载组合、支撑布置、截面选择、构造要求及连接等方面讨论了钢屋架设计应注意的事项,指出在钢屋架结构的设计过程中应首先确定合理的屋架形式,通过受力分析确定截面尺寸,并满足规范的相关构造要求。团队采用手工引导纤维束缠绕加高强纱绑束的成型工艺制备了截面形状为三角形的玻璃纤维/环氧全复合材料桁架。
通过分析发现,桁架的破坏主要是支座处的破坏,杆件并未发生屈曲,说明桁架的破坏不是强度破坏,而是节点连接起控制作用。认为在实际情况下桁架结构中,除轴向应力外,还不可避免的会产生弯曲应力,称为次应力。在屋盖结构设计上,团队结合实际工程设计,选取轻型薄壁钢管拱形屋盖的矢高、拱形桁架高度、杆件截面面积作为优化设计变量,以轻型钢管拱形屋盖的总造价最低为目标函数,建立了优化设计的数学模型
一、试验设计及方案
(一)试件尺寸
本次试验中的三角形平面屋架每榀宽 12.16m,高 2.33m,厚度为 70 mm,采用桁架体系。上弦杆和中央腹杆的截面宽度为 160 mm;下弦杆的截面宽度为 180 mm;其它杆件的截面宽度为 100 mm。试验中采用支座简支的形式模拟屋架[6]与墙板的连接,两支座间的净距为10.39m。为避免单榀屋架在竖直荷载作用下由于试验条件而造成偏心加载,最后导致失稳破坏。因此,试验采用两榀屋架为一组来进行试验,两榀屋架之间透过拉杆连接,屋架的前后距离则按照檩条长度来决定,试验中取檩条长度为 3.5m,并以此计算屋面荷载。
(二)测点布置
实验方案中,在每榀屋架上布置了 5 个位移计,以测量屋架在加载过程中竖向位移(挠度)的变化规律;此外,在每榀屋架上也布置了 7 个电阻应变片,以测量屋架在加载过程中应变的变化规律。对于电阻应变片的布置位置,首先要左右对称布置,其次要在上弦杆、腹杆以及下弦杆分别布置]。对于布置在上弦杆的应变片,考虑到节点间受力而导致上弦杆受弯,故布片时尽量布置在杆件反弯点处。前后两榀屋架的测点布置如图1 、图1 所示,其中位移计以Dx表示,应变片以x-x表示。
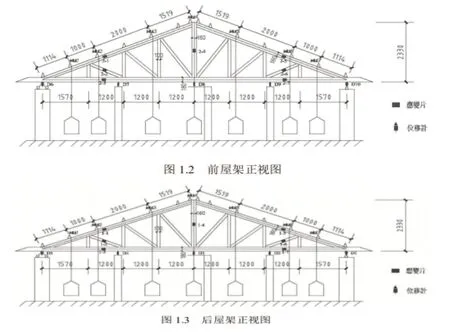
图2后屋架正视图
(三)屋架荷载计算
坡屋面做法为:沥青瓦片(0.07kN/m²)+20厚面板(0.20kN/m²)+檩条(0.53kN/根)+保温层(0.12kN/m²)+屋架(0.83kN/m²)+木吊顶(0.12kN/m²)
考虑到实际情况,计算中取不上人屋面活荷载为 0.5kN/m²,屋面积雪活荷载为 0.5kN/m²。表 1.1列出了由此计算出的屋架各种荷载组合的荷载值大小。
(四)加载装置及加载制度
由于试验为现场人工加载,试验时在每榀屋架的 7 个加载点上吊上钢索,钢索下挂吊篮,加载时根据每级荷载所需施加的负荷重量,往吊篮里放上铁块、砖块等重物。
试验过程中共分 8 级进行加载,列出各级加载所对应的状态。此外为考察屋架的弹性变形能力,在试验过程中,当加载到标准值组合后卸载到准永久组合(D5->D3),然后重新加载到设计值组合(D8)后卸载到标准值组合(D8->D5),然后在标准荷载组合水平下长期试验,看看徐变情况。
每榀屋架上各设 7 个加载点,详见图1 、图2 ,每个加载点按其左右两侧屋面面积的大小来分配负重,列出各加载点在该级状态时所施加上的荷载大小、该级荷载状态下各点所施加的荷载总和以及累加荷载大小
二、试验与数值模拟
(一)试验结果与分析
1.荷载-位移关系
实验方案中,在每榀屋架的两支座处、跨中处以及两 1 /4跨处布置了 5 个位移计[8]。在扣掉支座位移后,分别得到在不同荷载时屋架的跨中位移以及两 1 /4跨处的位移,所对应的荷载-位移曲线见。
跨中处的位移最大,左右 1 /4跨处的位移相近,这较能符合屋架在对称荷载作用下的位移变化规律。
此外,屋架在整个加载过程中都处于线弹性阶段,加载曲线的斜率基本一致;卸载过程中虽然有一定的残余变形,但在再加载过程中的曲线斜率仍能跟原本加载曲线的斜率吻合,说明屋架在整个加载过程中都维持在同一个受力变形阶段。
2.荷载-应变关系
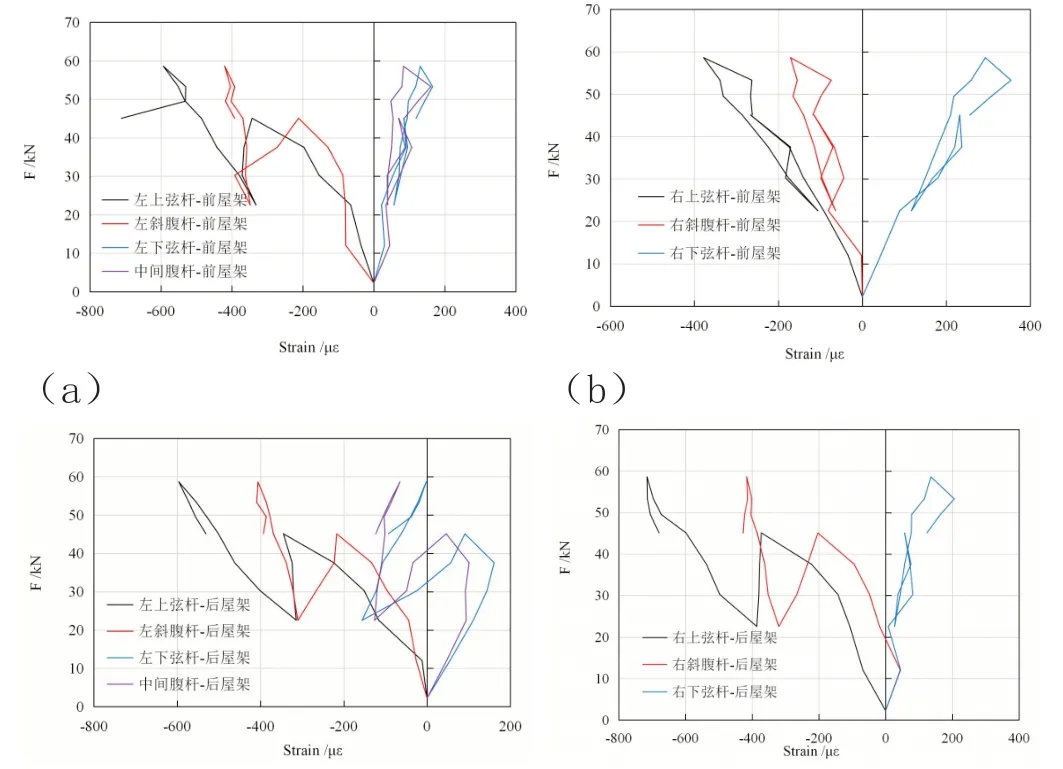
实验方案中,在每榀屋架各贴了 7 个应变片,图6 给出了两榀屋架实测的荷载-应变曲线。测试了根据该曲线,可以得出以下几点结论:
(1)屋架在整个加载过程中仍处于线弹性阶段,加载曲线的斜率跟再加载曲线的斜率仍能较好地符合。
(2)屋架的下弦杆和中间腹杆为拉杆;上弦杆和斜腹杆则为压杆。受力状态与计算机数值模拟结果接近。
(3)加载过程中后屋架的中间腹杆的受力状态从受拉变为受压,这可能与实验过程中前屋架右侧的支座翘起有关,可认为是实验现场所造成的原因。
(4)到达标准荷载时,屋架上弦杆测点的最大压应变在 385 µε 以内(前左上弦最大压应变在 343 µε,前右上弦最大压应变在 262 µε;后左上弦最大压应变在345µε,后右上弦最大压应变在 385 µε)。
(5)到达设计标准荷载时,屋架上弦杆测点的最大压应变在 715 µε以内(前左上弦最大压应变在 593 µε,前右上弦最大压应变在 378 µε;后左上弦最大压应变在 596 µε,后右上弦最大压应变在 715 μs。
3.跨中挠度
上图给出了前后两榀屋架在不同荷载级别时的荷载-跨中位移曲线。对于前一榀的屋架,当所有加缷载完成,即荷载回到标准值组合时,扣除支座位移后的跨中净位移为 7.53mm <l/250 =41.6mm,满足规范《GB50005-2003》中 4.2.7条对跨度/250的要求;当加载级数为第 8 级,即荷载达到由活载控制的设计值组合时,跨中净位移最大值为 9.05mm。
对于后一榀的屋架,当所有加缷载完成,即荷载回到标准值组合时,跨中净位移为 5.97mm,满足规范要求;当加载级数为第 8 级,即荷载达到由活载控制的设计值组合时,跨中净位移最大值为 7.29mm。
由于是短期加载试验,没有材料徐变的特征数据。现在的跨中最大变形只是最大允许变形的 1 /6.3,可以推断屋架的竖向刚度较大。
根据草拟中的设计规程,对于轻质复合屋架的变形限值要求,应考虑永久荷载、可变荷载、施工荷载、地震作用等荷载作用,按承载力极限状态和正常使用极限状态分别进行荷载效应组合,取对结构构件产生最不利效应的组合进行变形验算。因此,从上述分析中可知屋架在设计值组合作用下,屋架刚度依能满足该条文的要求。
(二)SAP2000数值模拟
1.屋架建模
按照屋架设计图纸,采用SAP2000程序中提供的Frame单元建立了一榀屋架的杆系有限元模型,假设屋架上下弦杆连续,腹杆与上下弦杆刚接。考虑到屋架腹杆轴线与弦杆轴线交点与上下弦杆截面中心线不重合,建模时按照节点刚域处理,将腹杆杆件交点按实际图纸情况来建模。
根据以往的楼板试验实测数据,推算出模型材料的弹模值为 15000 MPa,本次计算中材料弹性模量按照 15000 MPa设置。由于试验中采用 7 点加载的方式,建模时同样在屋架上弦杆 7 个檩条托位置上分别加上 7 个集中力。
图3给出了单榀屋架在标准值组合以及设计值组合荷载时的荷载分布图,其中荷载大小的单位为kN ∙m。
2.内力结果
图4给出了三角形桁架屋架上各杆件在标准荷载组合与设计荷载组合时的弯矩大小,其中单位为kN ∙m。
屋架上下弦杆弯矩最大的节间在端开间的节点附近,轴力最大的腹杆件是中间竖杆与紧邻端开间的第二开间。所以,在试验中监测的应变测点按照上述分析确定了应变测点布置,结果见图3 。
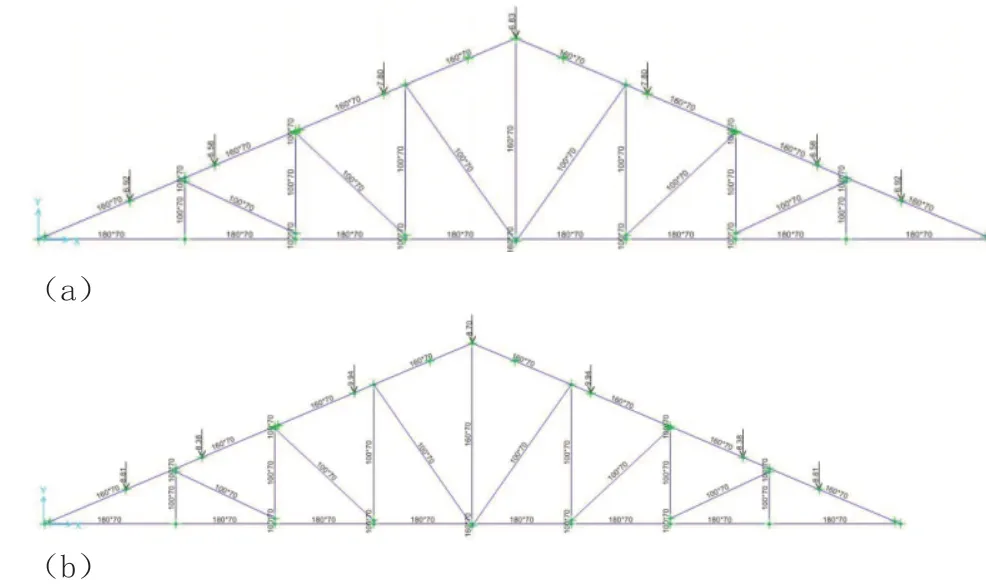
图3 荷载分布图
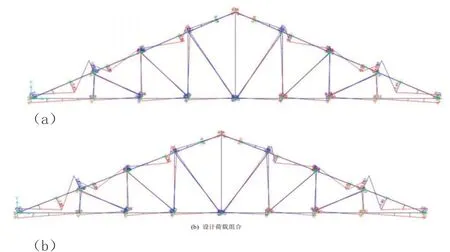
图4 弯矩图
3.屋架变形
图5给出了三角形桁架屋架在标准荷载组合与设计荷载组合时的跨中位移值,其位移计算值分别为7.38mm和9.40mm,可见与试验所得的数值已很接近,实际值更比计算值要少一些,这可能表明实际屋架的刚度比理论值还要大,材料实际的弹模值也可能比理论值更大一些。
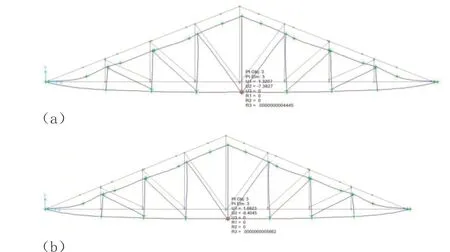
图5 跨中位移(a-标准荷载组合;b-设计荷载组合。单位:mm)
三、结论
基于对三角形轻质复合屋架的基本力学性能测试结果的分析与数值模拟,得到的以下结论:
(一)从屋架荷载-位移曲线看出,从开始加载到设计荷载组合的整个加载过程中,屋架处于线弹性受力,卸载与再加载曲线与原加载曲线斜率基本重合。
(二)透过荷载-跨中位移曲线,验证了屋架挠度在设计值组合荷载时屋架跨中最大,位移仅为允许变形(跨度/250)的 1 /5.3,考虑徐变的影响,屋架的跨中挠度能满足条文规定,说明屋架的刚度满足要求且有较大富裕。
(三)透过荷载-应变曲线同样验证了屋架处于线弹性受力外,证明了各杆件的受力状态与计算机数值模拟所得结果接近,说明屋架各杆件的受力状态符合预期。
(四)跨中位移实测值要比计算值小,说明屋架实际的刚度比理论值还要大。
