“一题一课”让解题教学走向简约、精准和高效——以一道多元变量的条件最值问题为例

李 湘 (江苏省无锡市辅仁高级中学 214123)

1 问题背景

美国著名数学教育家G·波利亚曾经说过：“掌握数学就意味着善于解题”． 数学解题为学生提供了一个应用数学知识、掌握数学思想和方法、提高分析问题、解决问题的能力的平台. 学习数学离不开解题，所以，解题教学成为数学教学的重要组成部分，贯穿了整个数学教学过程的始终． 加强解题教学是提升数学教学的重要前提． 如何上好习题课？怎样才能有效地提高解题教学的效益？这是每位数学教师都应认真思考和积极探索的问题．

题海战术的课堂节奏快、容量大，教师滔滔不绝地讲解，希望能给学生多灌输一些题型，多传授一些方法，课后再给出大量的习题让学生操练，而学生则忙于记录，稀有思考，课后的重复训练和大量刷题费时又费力，效果还差强人意． 针对这种现状，笔者通过调查分析，对解题教学的方式做了一些对比试验，感到“一题一课”具有简约、精准和高效的特点，不失为一种有效的方法．

所谓“一题一课”，就是对一道题或一个材料进行深入研究，认真琢磨其本质，通过纵横联系，将孤立问题“串”起来；通过课外拓展，让学生思维“飞”起来；基于学情，科学、合理、有序地组织学生进行相关的数学探索活动，从而完成一节课的教学任务，以此达成多维目标的过程．[1]下面记述一道多元变量的条件最值问题的教学过程，与同仁交流．

2 教学案例

2.1 原题呈现，聚焦学生的思维

这个问题综合性较强，难度较大，对学生有一定的挑战性，一经提出，学生就积极地展开思考，尝试求解． 但都未能成功．

师：在前面的学习中，我们研究过与其类似的问题吗？有没有积累过关于这一类问题的解题经验？

2.2 类题铺垫，引发学生的记忆

学生认真回忆，互相交流，反响热烈． 教师在学生讨论的基础上，给出以下问题作为铺垫，为解决原题提供知识和方法的储备．

师：先请大家看一个比较熟悉的问题．

问题2已知正实数x，y满足xy+x+y=3，则x+y的最小值是．

这是一道比较容易解决的问题，学生能够从不同的视角得到这个问题的不同解法．

师：生1利用已知条件，通过消元，转化为一元变量的最值问题，然后运用基本不等式求出了最小值． 非常好！

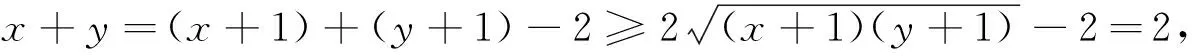
师：生2和生3的解法，虽然过程有所不同，但有一个共同的特点，就是无需消元，只需运用整体处理的方法，直接由基本不等式求出函数的最小值，显得既简洁又巧妙． 请大家再看下面的问题．

很快有学生想到先将目标函数变形简化，再运用基本不等式求出其最小值．

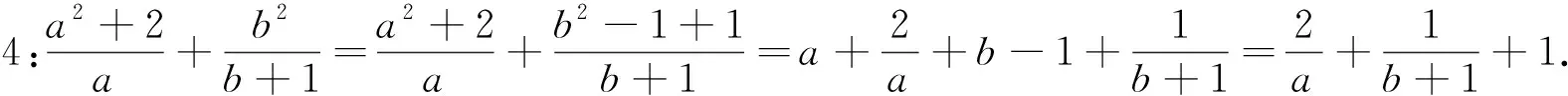
生众：可以的，也不难解决．

师：上面两题中都只涉及两个变量，有遇到过三个变量的问题吗？

师：同学们有什么想法吗？

师：这个想法不错，大家试试看．

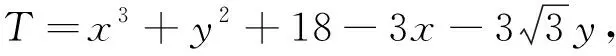
设f(x)=x3+18-3x，f′(x)=3x2-3． 令f′(x)=0，可得x=±1，

师：很好！现在请大家回过来看看，我们开始提出的问题，有办法解决了吗？

2.3 探索解法，提升学生的能力

学生交流讨论，探索原题的解法，很快就有同学取得了很好的进展．

2.4 变式引申，拓展学生的思维

师：上面我们从不同的视角探索了原题的解法，对这个问题，大家还有一些新的想法吗？能不能由原来的问题，提出一些新的问题来?

生9：我想啊，能求出W的最大值吗？如果将问题变成求W的取值范围，又怎么求解？

师：这个想法有见地． 我们解决一道数学问题，不能就题论题． 要善于从这道题出发，作一些变式，提出一些新的问题，将这道题的作用发挥到极致． 就今天的这个问题而言，大家能求出W的最大值吗？试试看．

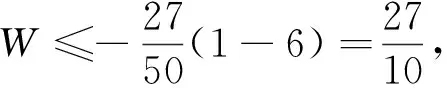
2.5 总结提炼，完善学生的认知

师：很快又到下课的时间了！请同学们回忆一下我们今天这节课的研究内容．

生11：今天这节课，我们主要研究了多元变量的条件最值问题的求解方法．

师：我们是怎样进行研究的？研究的方法是什么？

生12：我们从一道典型的问题出发，联想已经研究过的类似的问题，从不同的视角，运用一题多解与一题多变的方法，探索得出这一类问题的一般的解题方法．

师：通过这节课的学习，你有哪些收获？

生12：掌握了求解多元变量的条件最值问题的基本思维方法：一是利用已知条件消元，将其转化为一元变量的函数最值问题来处理，二是借助基本不等式整体求解．

生13：体会了等价转化、分类讨论、先猜后证、类比等数学思想和数学方法在解题中的应用．

师：运用基本不等式求最值，要注意什么？

生14：要关注“一正、二定、三相等”的条件，三者缺一不可！

师：求解一元变量的函数最值问题，常用的方法有哪些？

生15：可以借助函数的图象，利用函数的单调性、求导数的方法，也可以运用基本不等式．

师：对今天的问题，大家还能做哪些探究？课后不妨试一试.

3 教后反思

“一题一课”的学习模式最大的特点是“小切口，深挖掘”，对数学“题”进行深度挖掘，以“原题”为本，设计出不同层次的探究题，由浅入深，逐个击破，真正做到了深度学习，促使学生的数学思维从低阶逐步跨越到高阶思维．[1]本节课给出的原题即问题1综合性较强，难度较大，对学生有一定的挑战性． 对于多元变量的问题，处理的常用方法是消元法和基本不等式法，如何让学生体会这两种方法？本节课的一系列问题串，给学生铺设好了台阶，问题2和问题3难度适当提高，都能转化为一元函数，然后用基本不等式或者求导得到最值，也可以直接用基本不等式解决双元变量的最值． 问题4的设计是让学生感受从二元变量跨度到三元变量，通过问题4，学生能进一步体会消元的思想和方法，尤其是三元变量的消元方法得到进一步的强化，从而能顺利地解决开始给出的问题1． 这一串问题很好地体现了“一题一课”的选题原则:层次性、开发性、广延性． 问题的层次性让不同能力的学生在学力上得到不同的发展；问题的开放性让不同层次的学生都能参与；问题的广延性，易于学生发现问题并做进一步的探究和推广．[2]

波利亚曾形象地指出:“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找找，很可能附近就有好几个． ”数学问题好比蘑菇，成堆同根地出现． 在进行解题教学时，教师如果能够以具有典型性、可以发挥示范辐射作用的原题为出发点，运用“一题一课”的模式，开展“蘑菇式”的变式探究活动，既可以让原本较枯燥无味的解题课堂变得生机勃勃，也能收到“讲一题、通一类、得一法”的效果． 本节课的教学以一道题为主线，围绕着一个主题开展探索活动，揭示问题本质，提炼解题策略，挖掘知识之间的联系，渗透数学思想方法，显得简约、精准和高效. 研究的内容和方法可以在学生头脑中留下深刻的印象，不容易遗忘，使其课后再做类似的问题时感到得心应手，逐渐感到学习数学不再枯燥无味．

教学有法，教无定法． “教亦多术矣，运用在乎人”． 叶圣陶先生也曾经说过：“教师之为教，不在全盘授予，而在相机诱导． 必令学生运其才智，勤其练习，领悟之源广开，纯熟之功弥深，乃为善教者也”． 建议各位数学教师重视对解题教学的研究，努力探索和构建出更多的、适合学生的、行之有效的解题教学模式，帮助学生“跳出题海”，让学生在生动活泼、丰富多彩的探究活动中深化对知识的理解，提高应用所学知识分析问题和解决问题的能力，使我们的解题教学真正走向简约、精准和高效．