核心素养导向下数学运算能力的培养
2021-01-24钱桂荣江苏省锡山高级中学214174
钱桂荣 (江苏省锡山高级中学 214174)
《普通高中数学课程标准(2017年版)》(下称新课标)指出:数学运算与数学核心素养的其他五个要素构成一个有机整体,它们既相互独立,又相互交融. 在数学运算核心素养的形成过程中,要使学生能够理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得正确运算结果,以此进一步发展数学运算能力. 下面结合本人的教学实践,谈谈寻求提升学生运算能力的途径和方法.
1 明确运算对象,把握运算的指向性
新课标指出,数学运算是在明晰运算对象的基础上进行的. 在课堂教学中,通过理解运算对象的内容、运算对象的背景、运算对象所在的知识体系,多角度观察,实现运算对象的多元表征,并广泛联系相关知识,引导学生对已知与未知条件进行合理推断,揭示因果关系 (由因导果或执果索因),牢固掌握并灵活运用概念中所表现出的数量化、符号化的内涵,明确运算对象,把握运算的指向性.
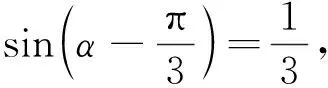
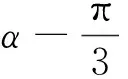
明确运算对象要求我们从多个视角审视运算对象:已知条件是什么?已知条件中的对象与所求对象有怎样的联系?从数量或图形角度看,它们有何内在联系?从数量的角度看,对应的数量、代数式、不等式、方程等是什么?从图形的角度看,图形由哪些基本的几何元素组成,这些几何元素之间有怎样的位置和数量关系?这些问题在运算一开始都要考虑清楚,做到运算指向正确、任务明确.
2 准确运用运算法则,把握运算的合理性
数学运算最基本的要求是准确运算,提升运算能力的关键在于整体把握概念的实质、深刻揭示运算的本质,理解算理,遵循运算的基本法则.
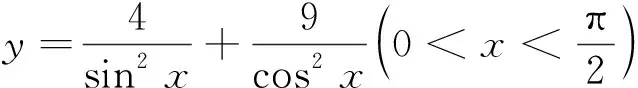
本题容易采用下面的错误解法:
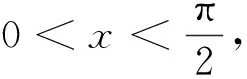
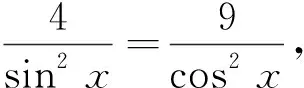
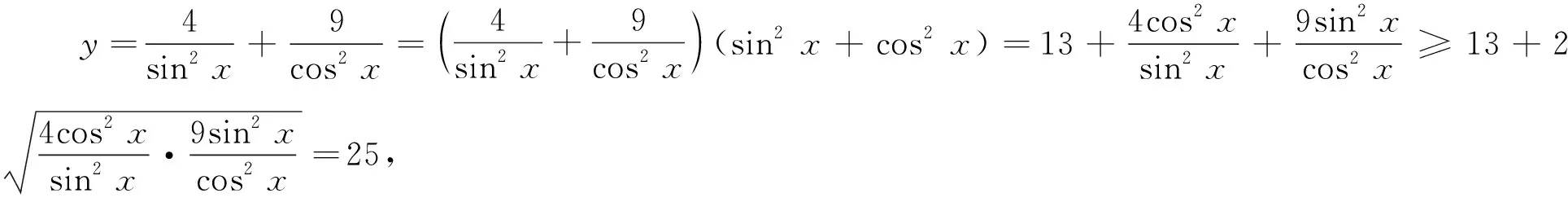
从上面例子可以看出,学生在运算中出现的错误从本质上说是对一些公式、定理、法则的本质掌握不够清楚,要提高运算的准确性,必须狠抓算法、算理的正确使用, 避免盲目套用公式法则而导致解题失误.
3 突出运算思路的寻找,把握运算的准确性
探究运算思路是在理解运算对象、运算法则的基础上,确定运算的具体指向,寻求运算的条理和头绪,是对数学运算的进一步推进. 运算思路合理与否,将决定运算的简与繁,甚至成与败,思路一旦确定,后面的工作便迎刃而解. 因此,探究运算思路是数学运算中的关键环节,通常也是最为困难的.
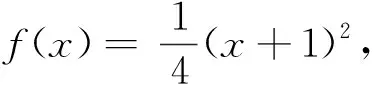
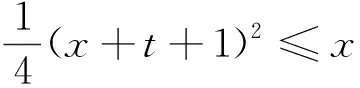
寻求运算思路时我们不妨可以借助波利亚的《怎样解题》中提供的各种途径:探寻包含在问题中的所有概念、公式、定理与方法,能不能利用它?联想与现在的问题有关且已解决的问题,考虑能不能利用或模仿它?仔细推敲每个条件或努力挖掘出隐含条件,尝试对问题进行转化与化归,正难则反. 如不能解决问题,能否找出一个更易着手的有关问题?一个更特殊的问题?一个类比的问题?一个更普遍的问题?
4 注重运算方法运用,把握运算的简捷性
运算速度是运算能力的重要标志,在数学教学中要强调在准确运算的前提下算得快,而要想算得快,就必须做到基本运算熟练,运算方法合理,运算途径简便. 同一个问题往往可用不同的思路和方法去解决,方法选择得越合理,运算速度也就会越快. 有些数学问题可根据题目的已知条件,利用有关概念、性质、法则进行简化运算,从而提高运算速度.
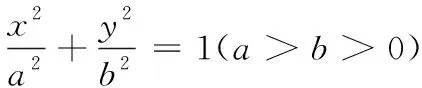
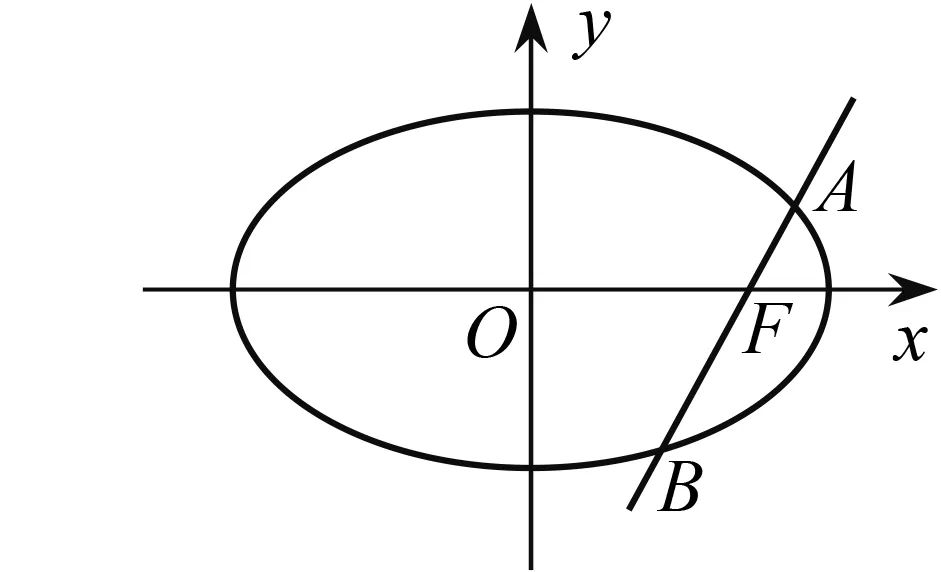
图1
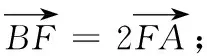

分析2 由于直线l过椭圆的右焦点,所以AF,BF都是椭圆的焦半径,因此可以考虑用椭圆的第二定义,通过数形结合来求解.
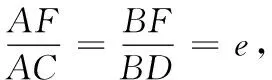
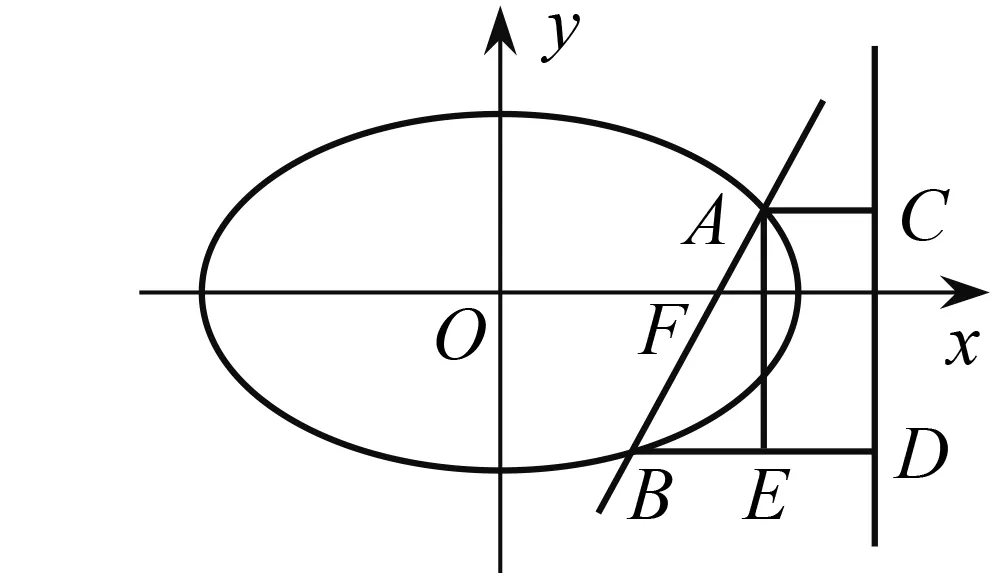
图2
上面两种解法中,第一种解法(即代数方法)是解决此类问题的通法,推理清晰严密,通过逐步消元求解,体现了解析几何的一般解题方法,但这种方法有一定的运算量. 第二种解法(即几何方法),过程比较简单,运算量很小,不易失误. 然而当改变条件,直线不经过焦点,此时AF,BF不是焦半径了,几何方法就不适合了,只能用通法(代数方法)来求解.
5 讲究运算的程序设计,把握运算的逻辑性
运算程序是对运算思路的具体落实,合理的运算程序设计是建立在对问题本质的思考之上的,它使运算按部就班地展开,易于驾驭,这对繁杂的运算尤为必要. 因此,应重视程序的设计,并相对“固化”一些常见且重要的运算程序,便于学生掌握.
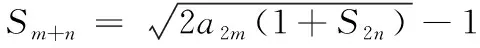


③-④,得an=(1+S2)qn-3(q-1)(n≥3). 接下来只要求出q,即可得到数列{an}的通项公式,只需要再用赋值法求出前几项即可.
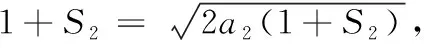
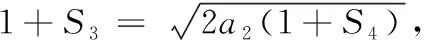
由⑤⑥得a3=4,a4=8,从而q=2. 所以an=(1+S2)qn-3(q-1)=2n-1(n≥3). 由于a1=1,a2=2也满足上式,故an=2n-1(n∈N*).
在上述问题的解决过程中,先由条件对正整数m,n任意变化时,等式恒成立,可先固定一个量m,然后得出Sn+1与S2n关系,再由n和n-1对应的两个等式成立,两边对应相除,得出{1+Sn}(n≥2)成等比数列,得到式子后再由an=Sn+1-Sn求得an(n≥3)关于n的关系式,最后对条件多次赋值求出数列前四项,这样既求出了公比,也说明n=1,n=2时也满足求出的当n≥3时的关系式,从而得到数列{an}的通项公式. 这些运算步骤都是数列问题的常用运算程序.
6 追求运算结果正确,把握运算的规范性
求得正确的运算结果,是进行数学运算的最终目的,处理不好,会前功尽弃. 运算技能必须通过长期的限时限量的训练才能得到提高. 由于高中数学教学内容多、任务重,而一些“烦琐”的运算很费时,在教学中教师要精心备课,在关键运算点上要舍得花时间,对求解过程中学生可能忽视的知识与方法、运算的程序与要点、或者可能产生的错误,以及计算时可能会遇到的障碍等,要进行全面的考察或预估,并在教学时重点加以关注. 在运算训练中,应重点强调基本运算、规范运算,这是提高运算准确率的基础. 在教学过程中充分让学生参与一些数与式的运算过程,如在学习解不等式、三角恒等变换及圆锥曲线时,要有意识地安排一些运算量较大的问题,以培养学生不怕繁难运算的意志品质,并对典型的运算障碍与错误经常进行剖析,促使学生在经常性的运算过程中提高熟练程度和准确率.
运算能力不能脱离具体的数学知识而孤立存在,也不能离开其他核心素养而独立发展. 它与观察能力、记忆能力、表达能力、理解能力以及思维能力等诸多因素互相渗透、协调发展. 培养与提高学生的运算能力是一项复杂的系统工程,要贯穿于数学教学的始终,要有计划、有目标、有意识地运用科学的方法进行长期的渗透和培养,使学生逐步领悟运算能力的实质,进而逐步提升思维能力和数学核心素养.
