基于IPSO的非晶合金干式变压器优化设计
2021-01-24刘道生魏博凯李家晨
刘道生,袁 威,魏博凯,李家晨
(江西理工大学 电气工程与自动化学院,赣州 341000)
0 引言
非晶合金干式变压器的铁心损耗较低,比传统硅钢片铁心变压器的空载损耗低75%,空载电流下降80%,是较理想的节能型变压器[1]。与硅钢铁心相比,非晶合金铁心的叠片系数低,制造工艺复杂,材料用量多,所以非晶合金干式变压器的价格比硅钢片干式变压器高[2]。为降低非晶合金干式变压器的材料成本,需对变压器设计方案进行优化。
在函数优化领域,基于现代智能理论的算法主要有遗传算法[3,4]、粒子群算法(Particle Swarm Optimization,PSO)[5]、混合蛙跳算法[6]和差分进化算法[7]等,计算效率相比穷举法和其他传统算法得到较大提高。在变压器优化设计领域,Zhang L.用多目标遗传算法对海上直流电网中的中频变压器损耗计算进行了优化[8]。Omorogiuwa E.提出一种与遗传算法相结合的非线性规划算法,并应用于变压器的优化设计问题,当优化不同容量的变压器时,该算法表现出一定的鲁棒性[9]。Zhang Y.P.在有限元方法基础上提出一种针对电力变压器参数优化设计的改进遗传算法[10]。Tsili M.针对变压器优化设计问题提出一种多目标对数正态-β差分进化算法,该算法有一定的能力保持迭代过程中种群的多样性和避免过早的收敛[11]。PSO因其独特的解空间搜索模式,在解决维数较多的工程优化问题时,收敛速度较其他算法快,但PSO存在易收敛于局部最优的问题。为解决PSO易收敛于局部最优的问题,本文提出一种自适应粒子交叉搜索策略,改进后的粒子群算法(Improved Particle Swarm Optimization,IPSO)提高了收敛成功率。
本文分析了非晶合金干式变压器优化设计的数学模型,描述了非晶合金干式变压器的人工优化计算过程,选取了优化变量,在此基础上设计了基于PSO的变压器材料成本优化模型,为增强PSO的搜索性能,提高收敛成功率,提出一种带自适应粒子交叉搜索策略的IPSO。对基于PSO和IPSO的变压器优化模型进行了实例优化,验证了IPSO比PSO拥有更好的搜索性能。对IPSO优化算法的研究有益于提高非晶合金干式变压器优化设计的效率,降低变压器的材料成本,提高非晶合金干式变压器的市场竞争力。
1 变压器优化设计的数学模型
非晶合金干式变压器优化设计的数学模型表述为:
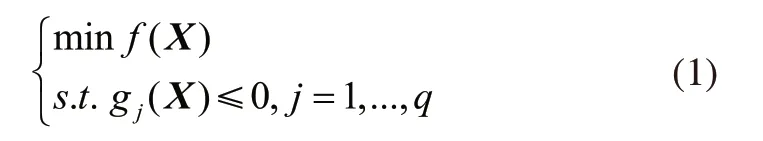
式中f(X)、gj(X)分别为目标函数和约束条,j表示约束条件序号,X为优化问题的解空间。模型求解即在解空间X内寻找目标函数f(X)最优且满足约束条件的方案。
1.1 目标函数和约束条件
根据优化目的选取变压器的材料成本为目标函数。表1为某厂家315kVA非晶合金干式变压器人工设计方案的成本参数,变压器材料成本主要有铁心、导线和夹件等成本,对各部分材料成本进行综合优化,以达到降低材料成本的目的。

表1 变压器材料成本参数
目标函数可表达如下:
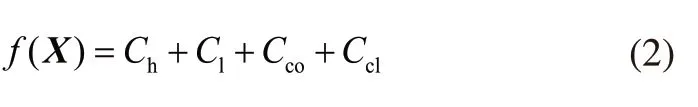
式中,Ch为高压导线成本,Cl为低压导线成本,Cco为铁心成本,Ccl为夹件成本。
在满足约束条件下,对变压器的优化才有意义。非晶合金干式变压器参数优化的主要约束条件如下:
1)空载损耗:P0≤Pm1,W;
2)空载电流:I0≤Im,%;
3)负载损耗:Pk≤Pm2,W;
4)短路阻抗:Umin≤Uz≤Umax,%;
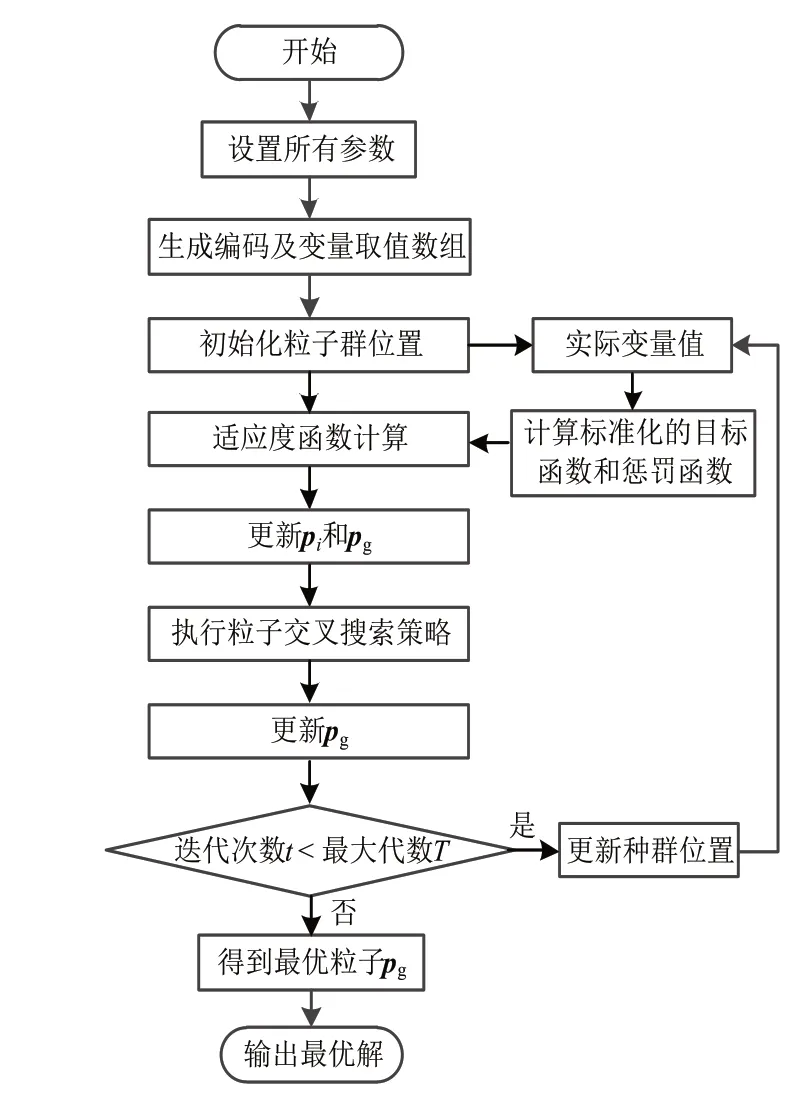
5)线圈温升:高压绕组温升T1 6)铁心磁通密度:Bmin≤B≤Bmax,T; 7)导线电流密度:J≤Jmax,A/mm2; 8)导线线规符合线规表; 9)变压器效率:E>Emin。 非晶合金干式变压器材料成本的人工优化计算过程如图1所示,跟穷举法相似,通过逐一计算解空间X内的所有变量组合,找到材料成本更优且满足约束条件的解。各优化变量的取值范围受当前经验的限制,不一定能找到满足约束条件的潜在的最优解。非晶合金干式变压器电磁参数的计算顺序依次为绕组参数、铁心参数、空载损耗、空载电流、负载损耗、阻抗电压、低压和高压绕组温升。 对材料成本和约束条件有影响的参数主要有绕组参数、铁心参数和绝缘参数等,根据设计原则仅选其中影响较大的参数作为优化变量,其他参数作为常量。 非晶合金材质铁心的片宽受工艺影响,有142.24mm、170.18mm和213.36mm三种规格可选。将铁心迭厚作为优化变量,对铁心性能和铁心成本进行调整。 图1 人工优化计算流程 如式(3)所示,磁通密度B是影响空载损耗P0大小的重要参数。 式中Pav、K0和GF分别为空载损耗系数、铁心单位损耗(W/kg)和铁心重量(kg)。 如式(4)所示,根据低压绕组匝数和铁心磁通密度的关系,将低压绕组匝数作为优化变量,对铁心磁通密度进行调整。 式中N为低压匝数,B为铁心磁通密度(T),f为频率(Hz),U为低压绕组相电压(V),S为铁心净截面积(m2)。 调整高压绕组成本Ch和低压绕组成本Cl,即调整绕组导线用材的总重量,将导线线规作为优化变量,实现导线用材调整,同时实现对温升和负载损耗进行调整。 如式(5)所示,高低压绕组间主空道宽度是影响有效总漏磁宽度λ的重要参数,进而影响阻抗电压电抗分量的大小,将其作为优化变量。 式中Ux为阻抗电压电抗分量,K为横向漏抗系数,In为低压额定相电流(A),W为低压每相匝数,∑Sd为总漏磁面积(m2),Hx为电抗高度(m),λ为有效总漏磁宽度(m),et为匝电势(V/匝)。 综上选用以下参数作为优化变量:铁心迭厚x1、低压匝数x2、低压绕组的线宽x3和线厚x4、高压绕组的线宽x5和线厚x6、高低压绕组间主空道宽x7,自变量间相互独立。上述7个变量实现了对材料成本和所有约束条件的调整,并间接影响铁心和绕组的结构。 PSO模仿鸟类的觅食过程对解空间进行迭代搜索,是一种基于群智能理论的优化算法,最早由社会心理学博士Kennedy和电子工程学博士Eberhart提出[5]。PSO用于无约束连续函数的优化,为将其应用于变压器的优化设计问题,引进变量离散化编码方法和惩罚函数形成基于PSO的变压器优化模型。 因制造工艺与标准化等限制,优化变量中涉及的高压和低压线规变量必须符合目前的工艺要求(标准线规表),是离散型非整数变量。受实际工艺精度影响,其他原本连续的优化变量全部作为离散变量处理。离散变量无法直接参与粒子群算法的迭代计算,采用整数编码的方式对变量进行编码。根据相应精度对所有自变量均采用以数字1开始的连续整数进行编码,PSO的解空间由变量的编码构成,编码对应实际变量值参与PSO的适应度计算。对变量进行编码时,根据实际设置变量的取值间隔即精度,如铝箔和铜箔的厚度以0.1mm为精度。 基于PSO[12,13]的变压器优化模型如下: 式(6)为PSO的迭代方程,w为惯性权重,wmax和wmin分别为惯性权重最大和最小值;T为总迭代次数,t为当前迭代次数;i表示粒子序号,i=1,2,3,···,M,M为粒子总数;Vi为第i个粒子的迭代速度;Xi为第i个粒子,对应的实际变量值为Yi,每个粒子分别对应一个变压器参数方案;pi为第i个粒子的历史最优位置;pg为粒子群的历史最优位置;c1、c2为大于零的学习因子;r1、r2是区间[0,1]上的随机数。 如式(6)所示,PSO通过粒子群位置的更新迭代实现对解空间的搜索。迭代过程每个粒子同时向自身的历史最优位置pi和粒子群的历史最优位置pg逼近,逼近速度Vi受惯性权重w影响。惯性权重w代表粒子有维持自己先前速度的趋势,较大的w使粒子群收敛速度较慢,偏向对解空间的全局搜索,较小w使粒子群收敛速度较快,偏向对解空间的局部搜索。粒子位置的优劣由适应度函数来评价,适应度越小,粒子位置越优。 式(7)为PSO的适应度函数fitness(Yi),引进惩罚函数对约束条件进行处理[14]。式(7)中p(Yi)为惩罚函数,由惩罚系数λ(t)和标准化约束违反程度vnorm(Yi)两部分构成,fnorm(Yi)为标准化目标函数值。惩罚函数的作用是增加不可行解的适应度,使适应度最佳的解是可行解,惩罚力度由惩罚系数λ(t)控制。 惩罚系数λ(t)的控制策略如式(8)所示,式中,t为当前迭代的代数,迭代前期t≤n1时,惩罚系数取最小值λmin;g为当前种群的最优解连续为不可行解的代数,当t>n1,g>y1时,增大惩罚系数,ɑ<1;y2>y1,增大惩罚系数后,当前种群最优解仍然是不可行解,则持续增大惩罚系数,µ<ɑ。 式(7)中标准化约束违反程度vnorm(Yi)和标准化目标函数fnorm(Yi)计算方式如下: 将粒子的第j个约束条件表述为: 第i个粒子在第j个约束条件上的约束违反程度Gj(Yi)为: 由于约束条件的差异,会出现约束条件对个体的约束违反程度v(Yi)起主导性作用,用标准化方法处理每个约束条件的违反程度。找到第一代粒子群中粒子违反各个约束条件的最大值Gmaxj: 第一代及后续粒子群的vnorm(Yi)定义为每个约束违反程度标准值的和,如下所示: 为均衡目标函数和约束条件之间差异,通过标准化方法使目标函数和vnorm(Yi)的量级相同。找到第一代粒子群的最小和最大目标函数值fmin和fmax: 为解决PSO易收敛于局部最优的问题,增强PSO的搜索能力,提高收敛成功率,提出一种自适应粒子交叉搜索策略。当粒子群的收敛陷入停滞时,通过粒子间的交叉,寻找新的全局最优解。在迭代过程,每个粒子以概率Pr与其他随机一个粒子进行交叉,概率Pr由当前粒子群的收敛情况决定,定义为: Re为pg连续不更新的代数,µ为交叉概率增加系数。 交叉操作定义为: 其中Xnew1和Xnew1是交叉操作生成的新粒子;X1是当前粒子,X2是X1外的随机粒子;Rnd是一个(0,1)区间的7维随机向量。计算Xnew1和Xnew1的适应度,如果比pg优则替换pg。 当进行上述粒子交叉后,pg仍然连续N代不更新时,粒子群有可能早熟陷入局部最优,将pg与随机粒子进行交叉,寻找新的全局最优解,交叉操作同上,如果新粒子比pg优,则新粒子替代pg。 IPSO的计算流程如图2所示。 IPSO的计算流程描述如下: 1)设置约束条件和变量取值范围等参数,生成变量的编码及对应的变量取值数组。 2)随机生成第一代粒子群的位置。 3)计算所有粒子的适应度,更新pi和pg。 4)根据当前pg的更新情况,执行粒子交叉搜索策略,如果发现比pg优的新粒子,则新粒子替换pg。 5)判断是否达到最大迭代次数,如果没有则根据pi和pg更新种群位置,进行下一次迭代计算,直到达到最大迭代次数。 图2 IPSO的计算流程 以厂家非晶合金干式变压器SCLBH15-315/10的人工设计方案为例,以降低材料成本为目标,满足约束条件下,对变压器方案进行优化。性能参数标准参考GBT 22072-2008。根据标准规定,单项损耗可在±10%,总损耗控制在±15%。考虑到制造误差与其他因素,单项损耗控制在5%,阻抗电压控制在±2.5%。根据非晶合金铁心固有特性,磁通密度为:1.200T≤B≤1.300T。 PSO和IPSO相同部分的参数设置:粒子个数M设置为100个;最大迭代代数T设置为4000代;学习因子c1和c2设置为2;最小惯性权重wmin设置为0.3,最大惯性权重wmax设置为1.1;最小惩罚系数λmin设置为1.5。IPSO的粒子交叉搜索策略参数设置:µ设置为0.005,N设置为700代。分别用PSO和IPSO进行优化。PSO和IPSO计算所得变压器设计方案如表2所示。 表2 PSO与IPSO优化方案 表2 (续) IPSO优化后的材料成本较人工设计方案降低9.23%。分别记录PSO和IPSO的200次计算结果,PSO收敛成功率为70.5%,IPSO收敛成功率为89%,IPSO的收敛成功率提高18.5%。 本文以降低非晶合金干式变压器的材料成本为目标,设计了基于PSO的变压器优化模型,提出了IPSO的改进策略,对非晶合金干式变压器的优化设计问题进行了研究。得到以下结论: 1)IPSO优化后的材料成本比人工设计方案降低9.23%。 2)基于IPSO的变压器优化模型收敛成功率为89%,相比PSO提高18.5%。 3)相比PSO,IPSO更容易寻得满足约束条件且成本更优的解,IPSO可应用于其他变压器优化设计问题。1.2 人工优化计算过程
1.3 优化变量选取
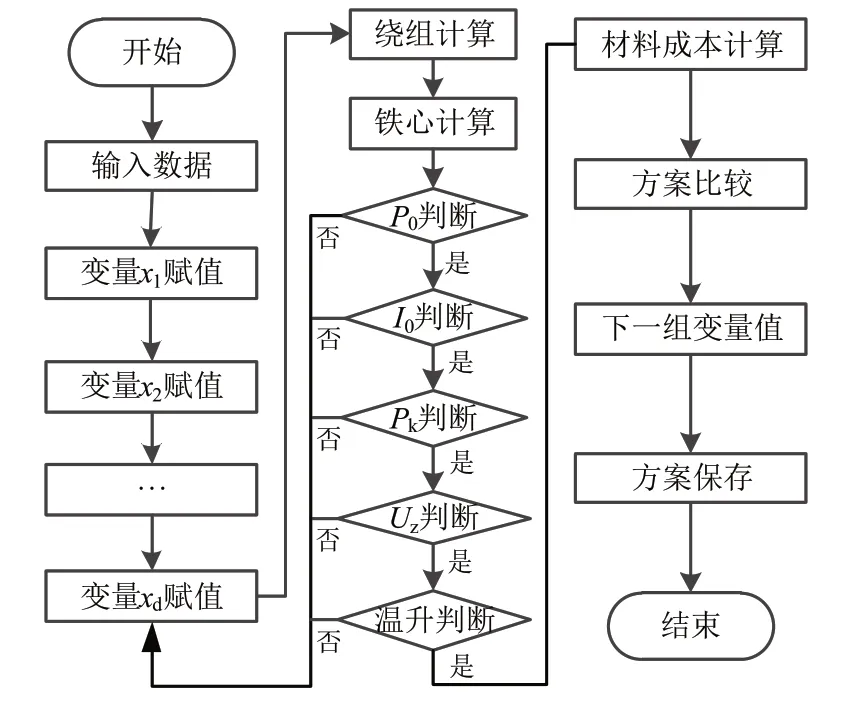
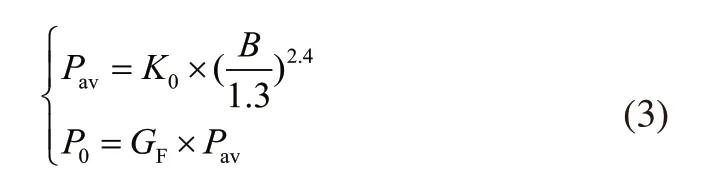
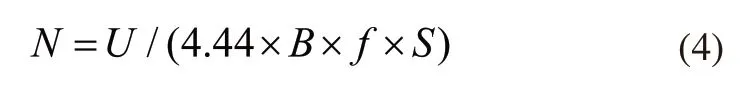
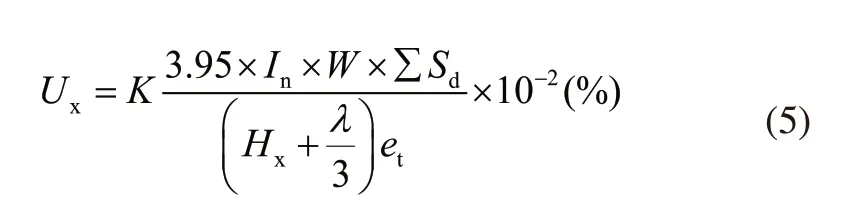
2 基于PSO的变压器优化模型
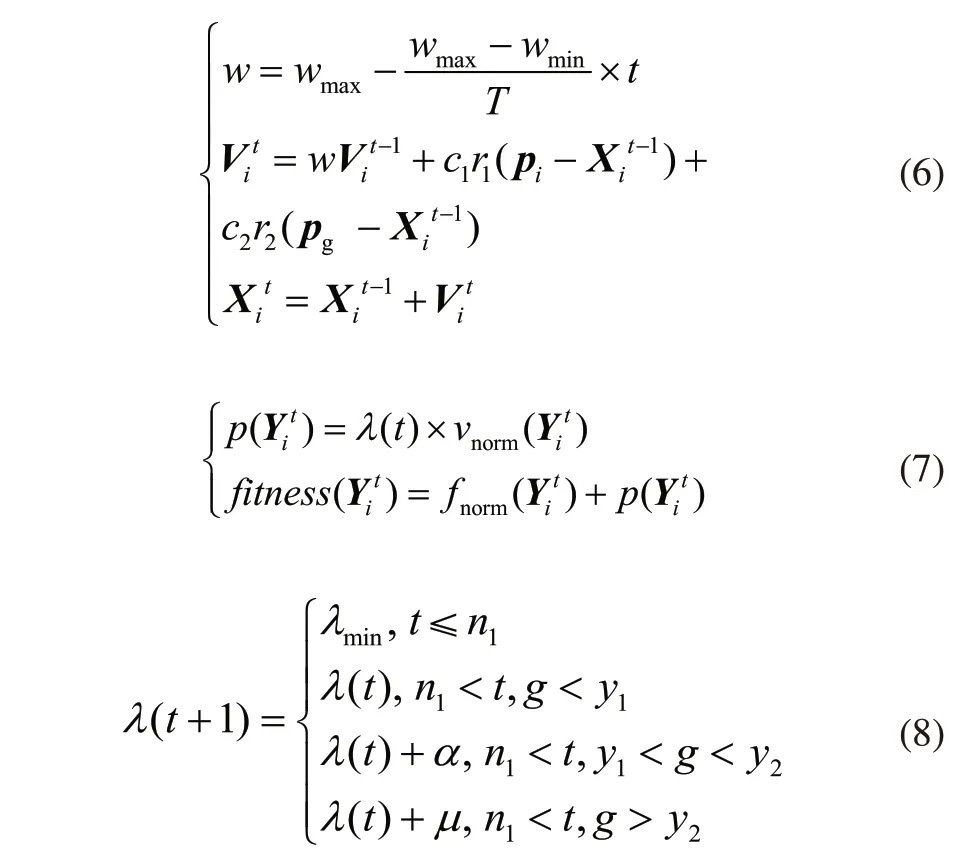
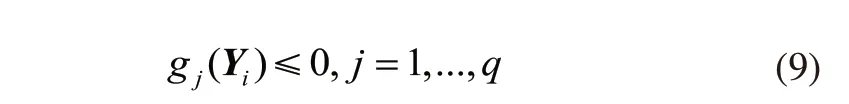
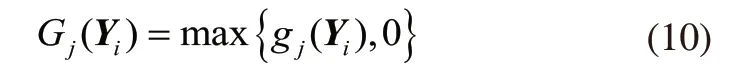
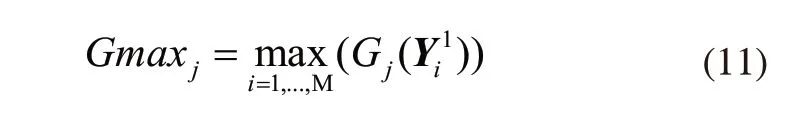
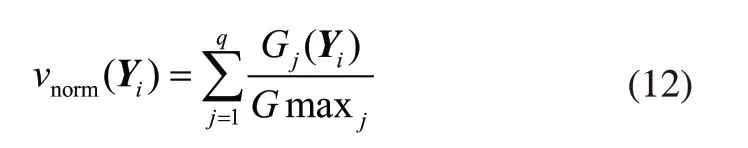

3 IPSO的改进策略


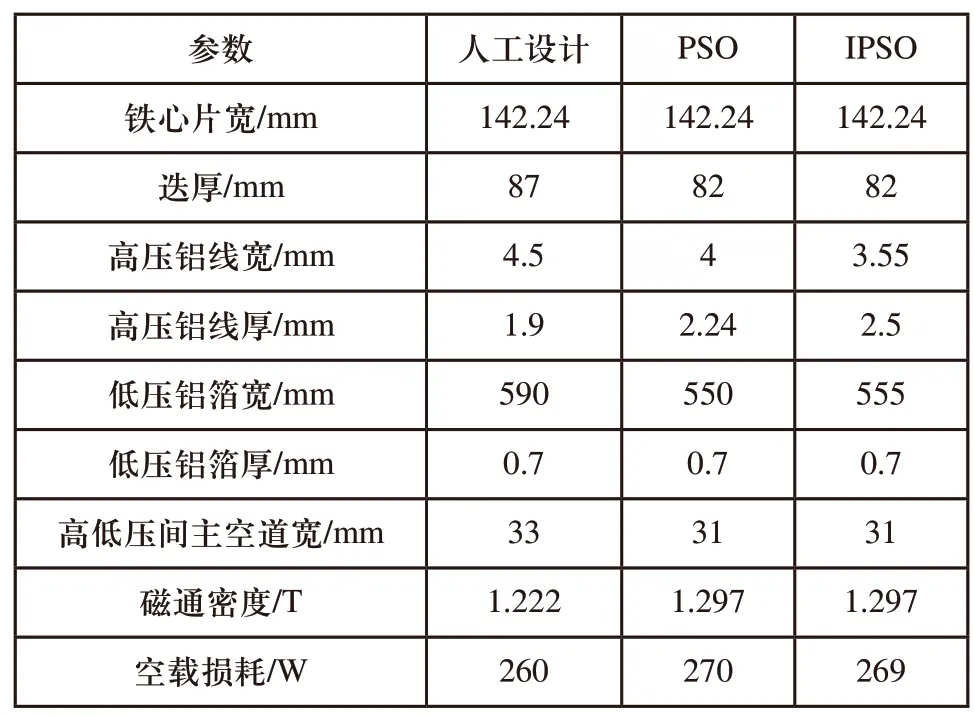
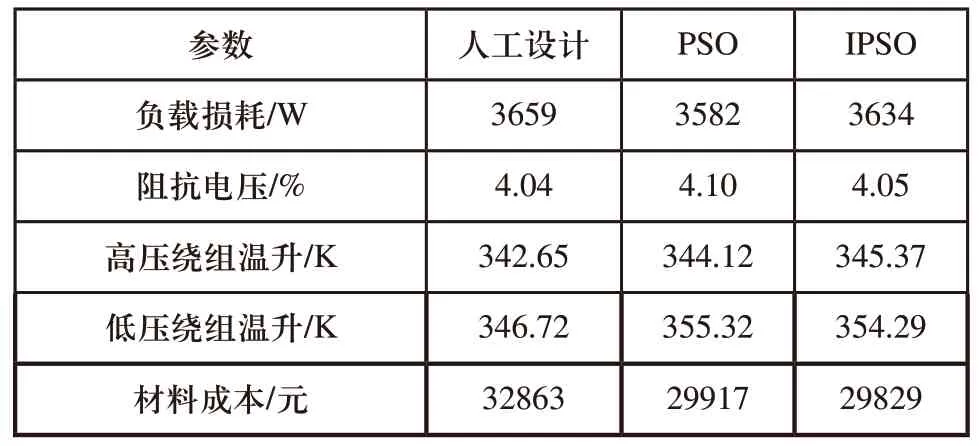
4 优化实例分析
5 结语
