静位移法求解理论力学中单自由度系统的自由振动问题
2021-01-23杨静宁赵永刚张亚民雷芳明
杨静宁,赵永刚*,张亚民,雷芳明
(1.兰州理工大学理学院,730050,兰州;2.中如建工集团有限公司,226500,江苏,南通)
0 引言
振动现象广泛存在于日常生活或生产实践中,也是工程实践中经常遇到的现象。而在工程实际中,经常遇到的最简单的振动系统则是单自由度系统,单自由度系统的自由振动反映了振动的一些最基本的规律。现行的理论力学教科书中,对振动系统(尤其是单自由度系统)微幅自由振动的固有频率求解均作了介绍。通常情况下,单自由度系统微幅自由振动的固有频率可通过振动的微分方程、能量法以及静位移(静变形)法3种途径来求解。但是现有教科书[1-5]以及相关资料[6-8]中大多通过微分方程和能量法来求解单自由度系统自由振动的固有频率,而对静位移法介绍甚少。本文将对静位移法做进一步的讨论和推广,得到了利用系统在外力(外力偶)作用下产生的静位移(静角位移)来求一般单自由度系统微幅自由振动固有频率的一般方法。
1 理论分析
如图1所示,铅垂平面内的质量-弹簧系统,弹簧(弹性元件)的刚性系数为k,物体(惯性元件)的质量为m。图1中δsd为物体产生的微小位移,称为静位移。以平衡位置为铅直坐标x的原点,其自由振动微分方程为[5]

图1 铅垂面内的质量-弹簧系统
(1)
固有频率为
(2)
一般的单自由度振动系统,均可简化成如图2所示的质量-弹簧系统。设等效在集中质量点的质量为m,等效刚性系数为k。在集中质量点加一振动方向上的小常力F,m产生的静位移为δsd,则δsd=F/k,以平衡位置为坐标x的原点,微幅自由振动时的振动方程与式(1)相同,固有频率为

图2 单自由度系统的简化模型
(3)
由振动方程可见,此常力并不影响系统自由振动的固有频率;而从式(3)可知,固有频率可通过外力F和外力作用下产生的静位移δsd来计算。
水平面内可绕定轴转动的刚体,如图3所示。盘簧的刚性系数为k,刚体绕定轴的转动惯量为J,在小的外力偶M作用下转过一个角度φsd=M/k,称为静角位移。以相对于平衡位置的转角φ为位移坐标,其自由振动微分方程为
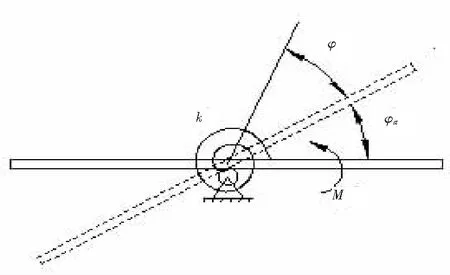
图3 水平面内可绕定轴转动的刚体
(4)
(5)
考虑一般的有转动的单自由度振动系统(如具有一个自由度的平移刚体或机构),由于是单自由度系统,运动中各构件角速度ωi的比例关系可由各构件间的运动关系确定。设系统微幅振动时,各构件对其各自速度瞬心的转动惯量为Ji,则定义系统对于第j个构件瞬心的广义转动惯量(平移刚体可设与运动方向垂直线上一点为其速度瞬心,按集中质量来计算,对广义转动惯量不产生影响)为
在第j个构件上作用一转动方向上的小力偶M,该构件在振动方向上绕瞬心转过一个微小转角φsd,此时振动系统的固有频率可表示为
(6)
2 实例分析
2.1 无转动的振动
如图4所示,斜面上的质量-弹簧系统,集中质量为m,弹簧的刚性系数为k,斜面的倾角为α,在重力作用下物体的静位移[5]为δsd=mgsinα/k,由式(3)可知其固有频率为

图4 斜面上的质量-弹簧系统
而由式(2)得出的结果是错误的,这是因为重力作用的方向和振动方向不同。
2.2 有转动的振动
如图5所示的有转动的系统,设绳子不可伸长,均质圆轮半径为r,对轮心的转动惯量为J,物体重P=mg,弹簧的刚性系数为k。不考虑轮轴的摩擦,则静位移δsd=P/k,静角位移φsd=δsd/r=P/(rk)。系统对轮心的广义转动惯量为JQ=J+mr2,根据式(6),系统的固有频率为

图5 有转动的单自由度系统
(7)
而根据式(3)得出的结果是错误的,这说明系统中的构件有转动时,式(3)将不再适用。
2.3 多机构的振动
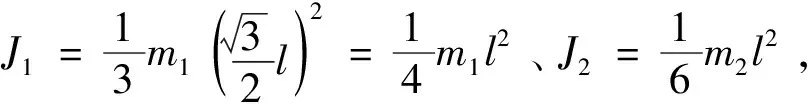
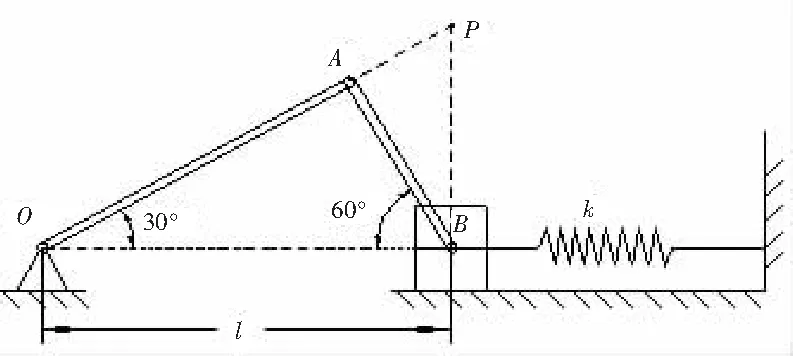
图6 与弹簧及滑块相连的曲柄连杆机构
(8)
这说明系统中的构件有转动时,可利用任一构件的静角位移来计算固有频率。
2.4 平面运动刚体的振动
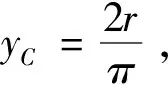
若水平面是光滑的,半圆环此时的速度瞬心在C点,如图7(b)所示,则固有频率
(9)
若水平面是粗糙的,半圆环微幅振动时为纯滚动,瞬心在A点,如图7(c)所示,则固有频率
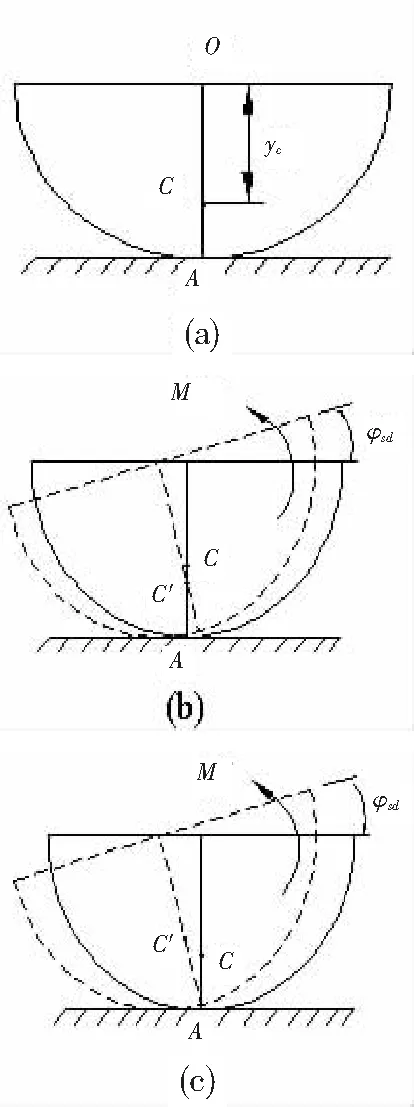
图7 垂直放置在水平面上做微幅自由振动的半圆环
(10)
可以看出,利用静位移法求解此振动系统固有频率简捷有效。
3 结束语
本文对静位移法作了进一步的讨论和推广,得到了利用系统在外力(外力偶)作用下产生的静位移(静角位移)来求一般单自由度系统微幅自由振动固有频率的一般方法,此方法简洁有效,可用于理论力学教学的补充。并得出如下结论。
1)单自由度系统微幅自由振动时的固有频率可利用在其振动方向上作用常力时产生的静位移,通过式(3)或式(6)计算求得。
2)所加的微小常力的方向必须是在振动方向上,静位移为此力作用处的微小位移。
3)系统中的构件没有转动时可应用式(3)计算其固有频率,若存在转动构件则必须应用式(6)。
4)应用式(6)时,可把机构的振动等效到任一转动刚体上,不影响固有频率计算结果的正确性。
