经验小波神经网络在电离层TEC短期预测中的应用
2021-01-23黄佳伟鲁铁定鲁春阳
黄佳伟,鲁铁定,鲁春阳,刘 盈
(1.东华理工大学测绘工程学院,330013,南昌;2.河南城建学院测绘与城市空间信息学院,467036,河南,平顶山;3.井冈山大学电子与信息工程学院,343009,江西,吉安)
0 引言
作为近地空间环境的重要组成部分,电离层对无线电通信、导航,卫星定位和遥感、遥测等有着重要的影响[1]。建立电离层总电子含量(Total Electric Contents,TEC)预测模型不仅为研究电离层的时空变化规律提供模型基础,也对研究地震异常探测等具有重要意义[2-3]。目前,国内外对电离层TEC值的预测根据时间长短可分为长期预测和短期预测。长期预测主要有利用TEC观测数据构建经验模型和参考电离层模型,如本特(Bent)模型、国际参考电离层模型IRI、克罗布歇(Klobuchar)模型等,其中以Klobuchar模型应用最广[1,4]。短期预测主要分为经典数学统计法和人工智能法,具体包括时间序列分析法、灰色预测模型和神经网络模型等[5-8]。如陈鹏等利用时间序列分析的方法对TEC数据进行预报,预测效果较好[5]。胡勇等提出将灰色理论运用于电离层预测当中,结果表明预测效果可行[6]。李淑慧等利用神经网络中的BP神经网络构建提前一天的TEC预报模型,结果表明预报模型可以反映不同季节的TEC变化特征[7]。然而电离层时空变化的复杂性给预报带来一定的影响,直接使用模型预测TEC数据无法达到满意的预报精度[8]。本文引入经验小波变换(Empirical Wavelet Transform,EWT)对电离层TEC数据进行分解,结合BP神经网络(Back Propagation Network)建立EWT-BP组合预测模型,以提高预报精度。
1 算法原理
1.1 BP神经网络模型
人工神经网络(Artificial Neural Network,ANN)是在现代神经科学研究成果的基础上提出的技术。它的基本处理单位为神经元,将大量的神经元以各种方式连接来建立非线性神经系统,处理各种复杂的数据。其中,在处理多维函数逼近、复杂模式识别和非线性时间序列预测等问题时,BP神经网络得到最广泛的应用。
BP神经网络(Back Propagation Network)又称反向传播神经网络,最早由Rumelhart和McClelland等科学家于1986年提出,因其具有较强的非线性映射能力和柔性的网络结构,在非线性时间序列预测方面的应用较为广泛[9]。图1为3层BP神经网络结构示意图,从图1中可以看出BP网络是由输入层、隐含层和输出层3部分组成的,其中隐含层可以有一层或多层。相邻层次的神经元之间实现全连接,而独立层次的神经元之间无任何连接。
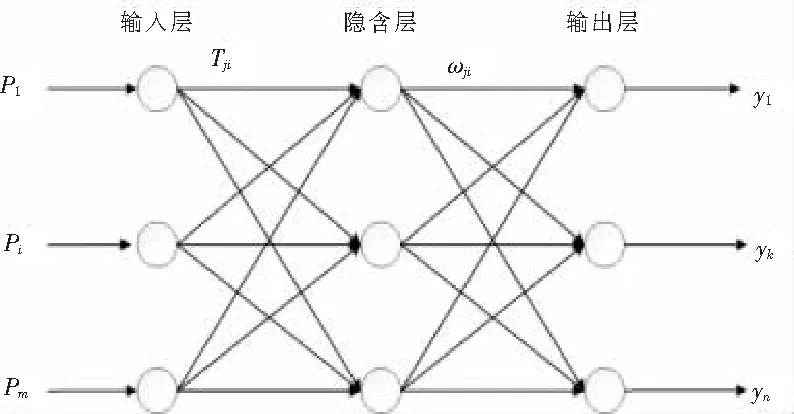
图1 3层BP网络结构图
BP神经网络的构建可分两步过程进行,即信号的前向传播和误差的反向传播,通过不断调整神经元之间的网络参数(权值和阈值),使实际输出逼近期望输出,达到最小误差均方差,其具体步骤如下[9]。
1.1.1 信号的前向传播 选择一组数据训练样本,将其分为输入数据和期望的输出数据;输入数据从输入层进入到神经网络,经过隐含层逐层处理后作用于输出层,经过非线性变换产生输出信号;计算网络输出和期望输出的误差函数,若误差满足目标要求,则网络建立成功,否则进入反向传播过程。
1.1.2 误差的反向传播 反向传播时,将输出误差通过隐含层向输入层逐层反转,将误差分摊给各层的所有神经元,已从各层收集的误差信号作为调整权值和阈值的依据。通过不断修正输入层与隐含层的权值和阈值以及隐含层和输出层的权值和阈值,使误差函数沿梯度方向下降,直到整个训练样本的误差达到要求为止。
误差函数[10]可表达为:
(1)
(2)
式中:p为数据个数,k为迭代次数,tl为期望输出,Ol为神经网络现行输出,ek为单个数据误差函数,E为总体误差函数。
1.2 经验小波变换
经验小波变换(Empirical Wavelet Transform,EWT)是Gilles[11]及其团队于2013年提出的一种基于信号频谱划分的信号处理新方法。与EMD缺乏严格的理论支撑不同,EWT依靠小波分析理论框架,根据信号自身性质产生基函数。其核心思想是根据信号频谱划分结果建立小波滤波器组,来提取信号的不同模态[12]。
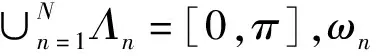
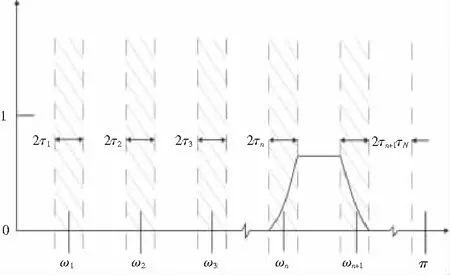
图2 傅里叶频谱划分
经验尺度函数可表达为:
(3)
经验小波函数可表达为:
(4)
其中τn和β(x)可表达为:
(5)
重构的原始信号可表达为:
(6)
经验小波分解的模态可定义为:
(7)
(8)
1.3 EWT-BP组合模型的建立
图3为EWT-BP模型算法流程图。
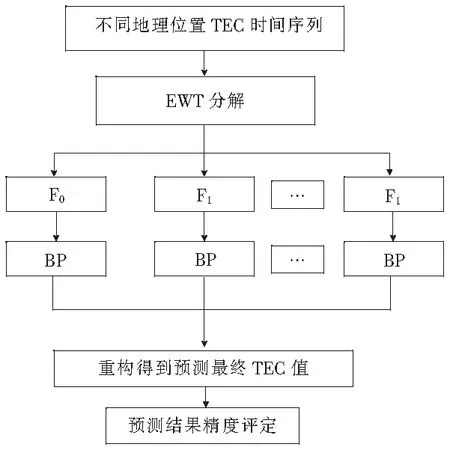
图3 EWT-BP算法流程图
将EWT算法应用到电离层TEC数据处理当中,首先利用EWT将不同位置处的TEC时间序列进行分解,得到不同模态分量的子时间序列,再利用BP神经网络对不同分量进行预测,预测结果叠加得到最终预测值。具体步骤如下。
1)利用EWT将TEC时间序列x(t)分解为一个经验尺度分量f0,代表信号整体变化趋势,k个经验小波分量fi,代表信号不同频域特征,即:
(9)
2)对分解后的经验尺度分量和经验小波分量分别建立BP网络模型进行预测,叠加分量预测结果得到最终TEC预测值。为减小叠加误差对最终TEC值的影响,因其信号能量主要集中在经验尺度分量和前2个经验小波分量,只取EWT分解的经验尺度分量f0和经验小波分量f1和f2,其结果不会对预测效果产生太大影响[13]。以IGS中心发布的TEC值作对比数据,采用日平均相对精度P和均方根误差RMSE作为评定预测效果的指标,可表达为:
P=1-|It-I|/I
(10)
(11)
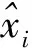
2 实验结果与分析
提取IGS中心提供的2010年电离层格网数据进行实验,参照文献[8],分别选取年积日为1~30、101~130、201~230和301~330 的4个不同时间段低纬(a.15°N,125°E)、中纬(b.45°N,60°W;c.45°N,125°E)、高纬(d.75°N,125°E)的TEC时间序列进行实验,每个时间段的年积日个数为30。将前24 d的数据作为输入,第25天的数据作为输出,组成训练样本,第2天到第25天的数据作为输入,来预测第26天的数据,以此类推,预测后5 d的数据,后5 d的数据作为真实值来检测模型预测效果。
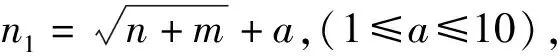
以年积日201~230时间段为例进行具体分析,对比分析EWT-BP组合模型和单一BP模型的预测效果。图4为年积日226~230的4个不同地理位置2种模型的TEC预测结果与TEC真实值对比图。其中横坐标为5 d内预测历元的个数,时间间隔为2 h;纵坐标为TEC值,单位为TECU的个数,1 TECU=1016e/m2。图4结果显示,相对于单一BP模型的预测结果,EWT-BP模型预测结果与真实值更加吻合,预测误差更小,表明EWT-BP模型能够更好地反映电离层TEC的变化特征,预测效果更优。
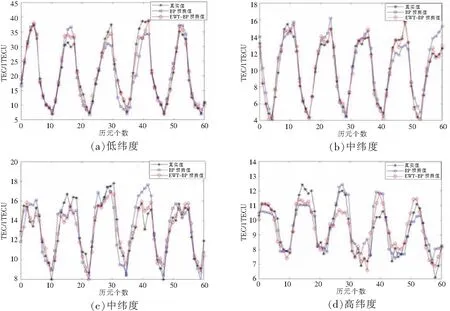
图4 不同地理位置2种模型的预报TEC值对比图
表1从整体上反映了2种模型的残差误差分布情况。从表1可以看出,BP神经网络模型预报的5 d内平均残差绝对值小于1个TECU占比为66.8%,平均残差绝对值大于3个TECU占比为6.4%;而EWT-BP模型预报的5 d内平均残差绝对值小于1个TECU占比为79.7%,平均残差绝对值大于3个TECU占比为2%。结果表明,组合模型的预测效果整体上要优于单一模型的预测效果,与图4结果相符。

表1 BP模型和EWT-BP模型的残差绝对值Δ(以TECU为单位计数)分类百分比/%
表2给出了不同地理位置的误差情况对比表。从表2中可以看出,同一地理位置,EWT-BP模型预测的相对精度普遍要比单一BP模型的相对精度要高,均方根误差普遍比单一BP模型的均方根误差要小,结果表明经验小波神经网络的预测效果要优于单一神经网络的预测效果。同一经度,均方根误差随着纬度的增加而减小,相对精度则未体现相同的变化趋势,其与不同位置处的TEC值大小相关。同一纬度不同经度间误差变化不明显。
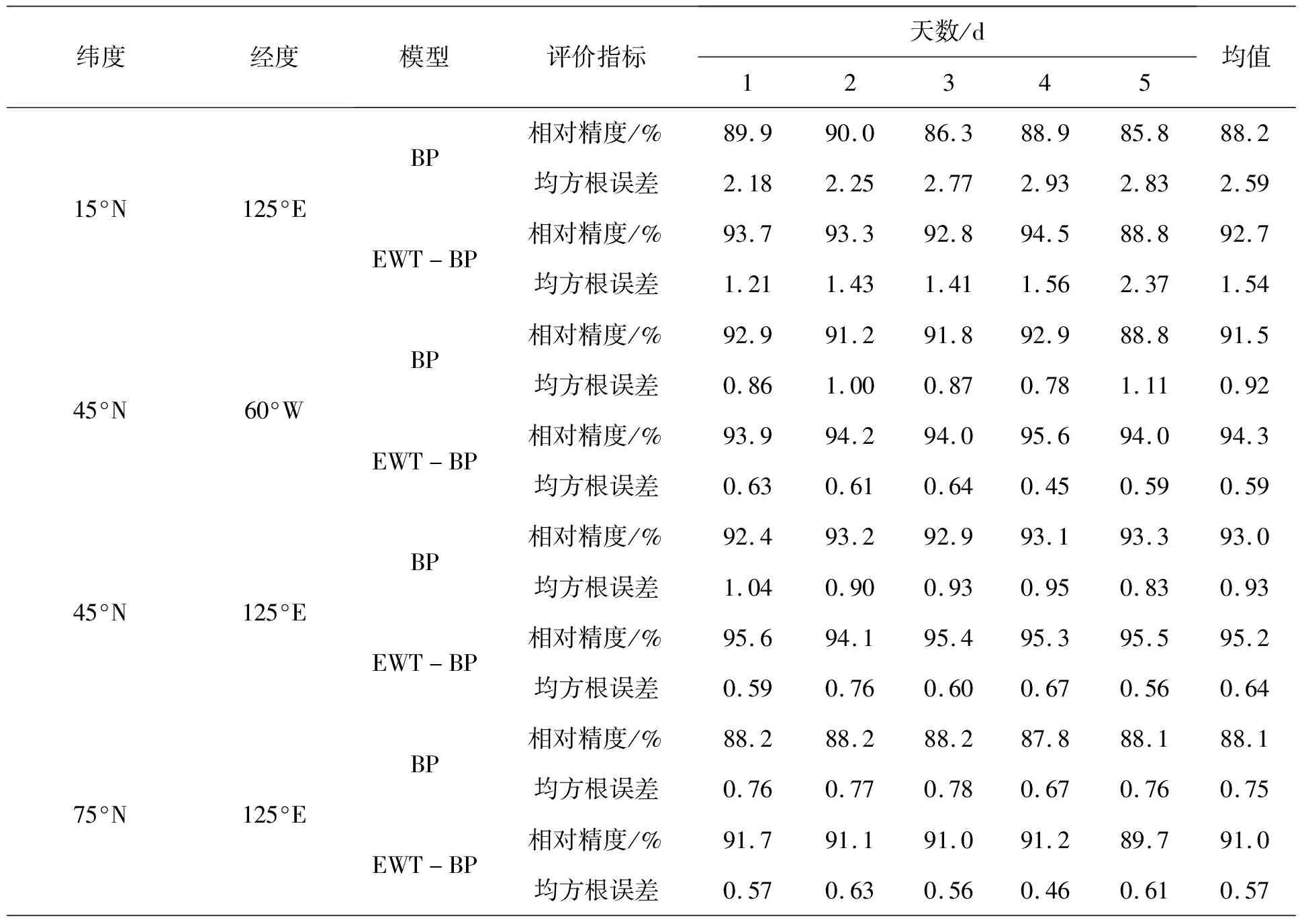
表2 不同地理位置5 d内平均预测误差情况对比表
表3为4个时段误差情况对比表,表3中显示BP模型预测的平均相对精度为90.2%,均方根误差为1.3;而EWT-BP模型预测的平均相对精度为93.2%,均方根误差为0.83。整体结果表明,EWT-BP模型的预测效果优于单一BP模型的预测效果。
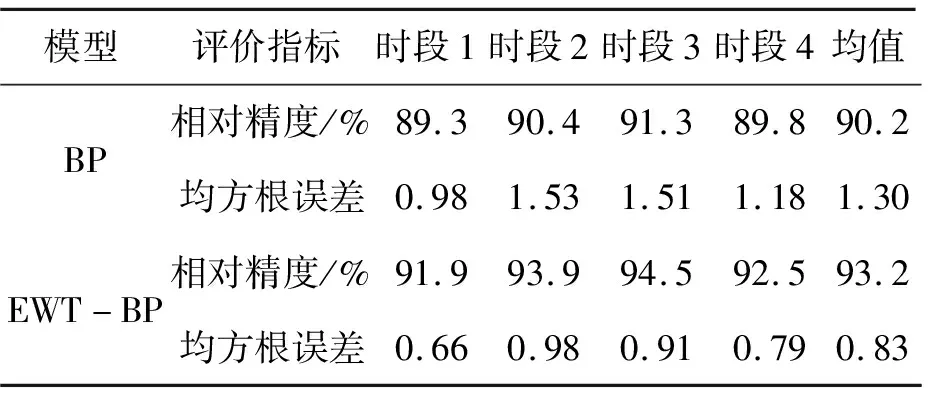
表3 4个时段平均预测误差情况对比表
3 结论
采用IGS中心提供的电离层格网数据进行实验,验证了EWT-BP神经网络模型预测的有效性,并与单一BP模型预测效果进行对比分析得出以下结论。
1)利用EWT对电离层TEC时间序列数据进行分解,对分解的各分量进行BP预测,预测结果叠加得到最终TEC值,并与TEC真实值进行对比。结果表明,EWT-BP预测模型能够有效地反映电离层TEC的变化特征。
2)对比单一神经网络模型的预测结果,组合模型预测的平均相对精度提高了3%,均方根误差减小了0.47,表明组合模型的预测效果更优。
本文将经验小波变换运用到非线性时间序列当中,给类似特征的时间序列预测提供了一个新思路。但是电离层复杂多变的时空特性给模型预测带来一定困难,此外神经网络预测模型主观性强的缺点也有待进一步解决。建立一个预测精度更高,稳定性更强的电离层预测模型还有待进一步的研究。
致谢:感谢IGS中心提供的电离层TEC数据!
